Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.30 no.1 Bogotá Apr. 2010
Julio César Caicedo Caicedo1 y José Nelson Pérez Castillo2
1Ingeniero de sistemas, Universidad de Nariño, Pasto, Colombia. M.Sc., en Ciencias de la Información y las Comunicaciones, Universidad Distrital Francisco José de Caldas, Bogotá, Colombia. Gerente de Proyectos, DB-System, Bogotá, Colombia. juliocaicedo@gmail.com 2Ingeniero de sistemas, Universidad Distrital Francisco José de Caldas, Colombia. Ph.D., en Informática, Universidad de Oviedo, España. Profesor Titular, Universidad Distrital Francisco José de Caldas, Colombia. Director, grupo de investigación GICOGE. nelsonp@udistrital.edu.co, jnperezc@gmail.com
RESUMEN
La integración de los avances en computación orientada a servicios, con aquellos alcanzados por la tecnología de la web y la inteligencia computacional, facilita el desarrollo de aplicaciones complejas para la solución de problemas de manera transversa en los diversos ámbitos de la investigación científica y tecnológica. Desde el campo de la inteligencia computacional la teoría de los conjuntos aproximados aporta un sólido fundamento teórico al razonamiento cualitativo exigido por el análisis de datos, caracterizados por la incertidumbre generada por la vaguedad e imprecisión asociada a éstos. El presente trabajo describe el desarrollo de un servicio web inteligente aplicado al procesamiento digital de imágenes, ilustrando las bondades de los conjuntos aproximados, para abordar de modo flexible y supervisado la clasificación de los pixeles asociados a ellas.
Palabras clave: conjuntos aproximados, inseparabilidad, aproximación inferior, aproximación superior, sistema de decisión, servicio web, imagen digital.
ABSTRACT
Integrating recent developments in service-orientated computing, Web technologies and computational intelligence has facilitated the development of applications for solving complex problems in several fields of scientific and technological research. Rough sets theory provides a solid theoretical background within the computational intelligence (CI) field for the qualitative reasoning re-quired for analysing datasets loaded with uncertainties due to the vagueness and lack of precision associated with them. This paper describes the development of an intelligent Web service to process digital imagery, demonstrating the benefits of rough sets theory in dealing with the flexible supervised classification of the pixels associated with them.
Keywords: rough sets, indiscernibility, lower approximation, upper approximation, decision system, Web service, digital image.
Recibido: marzo 18 de 2009 Aceptado: abril 05 de 2010
Introducción
La propuesta de un servicio web inteligente para la clasificación de imágenes digitales implica la integración sinérgica de los conceptos fundamentales del ámbito de la computación orientada a servicios, su integración al avance incontenible del desarrollo tecnológico de la web y el uso de técnicas avanzadas de inteligencia computacional. De tal manera, este trabajo se enmarca en el ámbito de la denominada inteligencia computacional web (Zhang, 2002).
Los servicios se conciben como un medio para la construcción de aplicaciones de procesamiento distribuido más flexibles y acordes a las necesidades del desarrollo social actual. En tal sentido cobra validez el no sólo hablar de servicios, sino también el desarrollar aplicaciones a partir del paradigma de computación orientada a ellos.
Indudablemente la combinación de la web y la computación orientada a servicios dio lugar a uno de los desarrollos tecnológicos más exitosos y establecidos del siglo XXI, conocidos como servicios web. No obstante, el desarrollo de aplicaciones complejas orientadas a servicios, exige el concurso de áreas tan importantes de las ciencias de la computación como la denominada inteligencia computacional.
En el caso específico de la clasificación de imágenes digitales, en la literatura es bien conocido el concurso de las redes neuronales artificiales (Benediktsson, 1997), la lógica difusa (Mannan, 1998), la computación evolucionaria (Bandyopadhyay, 2005), las máquinas vectores soporte (Bazi, 2006).
En este documento se describe un servicio web inteligente para la clasificación de imágenes digitales, denominándolo así dado que para su realización se hizo uso de la inteligencia computacional, recurriendo a la teoría de los conjuntos aproximados (Pawlak, 1991). A tal efecto, se describen brevemente los servicios web, luego se reseña la teoría de conjuntos aproximadas y se discute el problema de la clasificación de imágenes digitales, abordando luego, de manera específica, el servicio web inteligente de clasificación de imágenes y las conclusiones del trabajo realizado.
Los servicios web
Los servicios Web proveen un medio estandarizado para el logro de la interoperabilidad de aplicaciones informáticas que se ejecutan sobre una variedad de plataformas y entornos computacionales. La definición del World Wide Web Consortium (W3C) establece que "un servicio web es un sistema de software que se diceña para soportar la acción interoperable máquina a máquina sobre una red. Tiene una interfaz descrita en un formato procesable por la máquina, específicamente Web Service Definition Language (WSDL)" (W3C, 2004). Otros sistemas interactúan con el servicio web de manera prescrita por su descripción, usando mensajes que siguen el Simple Object Access Protocol (SOAP), típicamente transportados usando HTTP con una serialización XML en conjunción con otros estándares web relacionados.
SOAP es un protocolo que se usa para el intercambio de información estructurada, en un ambiente de procesamiento distribuido; sigue un paradigma de intercambio de mensajes unidireccional sin mantenimiento de información de estado; no obstante, puede usarse para crear patrones de interacción más complejos. Los mensajes SOAP se codifican en XML.
La comunicación entre servicios web se inicia por parte de otras entidades de software que a su vez envían mensajes codificados en XML. El servicio en sí mismo es una funcionalidad abstracta, cuya implementación puede ser reemplazada, mientras que su concepción sigue siendo la misma (Cerami, 2002).
Los clientes de los servicios web deben ser capaces de encontrar los servicios apropiados a sus necesidades. El proceso se denomina descubrimiento de servicios web. Para tal fin, la especificación denominada Universal Description, Discovery and Integrations (UDDI), define un registro distribuido de servicios (UDDI, 2000).
El diseño de un servicio web inteligente implica incorporarle internamente un mecanismo de inferencia que en el caso particular del presente trabajo se traduce en la realización de un mecanismo de razonamiento en condiciones de incertidumbre, recurriendo al uso de los conjuntos aproximados.
Teoría de conjuntos aproximados
La teoría de los conjuntos aproximados se debe a Zdzislaw Pawlak y su equipo (Pawlak, 1995). Esta corriente de pensamiento asume que, frente al problema de la clasificación, cada objeto del universo del discurso tiene información asociada (Pawlak, 1991).
La teoría de los conjuntos aproximados permite descubrir conocimiento, ya que es posible construir una clasificación (Xu, 2002) a partir de la aproximación inferior y la aproximación superior de un conjunto. El pensamiento relacionado con los conjuntos aproximados surgió en el seno del aprendizaje supervisado, donde las colecciones de datos se refieren a un universo de objetos definidos por un conjunto de atributos y en donde cada objeto pertenece a una clase predefinida por uno de los atributos que se etiqueta como el atributo de decisión.
Base de conocimiento
De acuerdo a Pawlak, se parte de un conjunto finito: 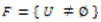 , donde U es el universo de objetos de interés. Cualquier sub-conjunto:
, donde U es el universo de objetos de interés. Cualquier sub-conjunto: 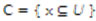 del universo, se denomina como concep-to o categoría en U, y una familia de categorías en U se define co-mo el conocimiento abstracto acerca de U. Por formalidad se ad-mite que el conjunto:
del universo, se denomina como concep-to o categoría en U, y una familia de categorías en U se define co-mo el conocimiento abstracto acerca de U. Por formalidad se ad-mite que el conjunto: 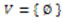 (conjunto vacío) es un concepto.
(conjunto vacío) es un concepto.
El interés principal radica en las categorías que forman una partición (clasificación) de un universo U conocido. Por ejemplo, en la familia:

Una familia de clasificaciones sobre U puede llamarse una base de conocimiento basesobre U, representando una variedad de posibilidades de clasificación, verbigracia, de acuerdo al color, la temperatura, o valores numéricos (Li et ál., 2005).
Una base de conocimiento (simbolizada por K) puede expresarse como 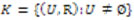 , U es un conjunto finito llamado universo, y R es una relación de equivalencia sobre U (o familia de clases de equivalencia).
, U es un conjunto finito llamado universo, y R es una relación de equivalencia sobre U (o familia de clases de equivalencia).
Sistema de información
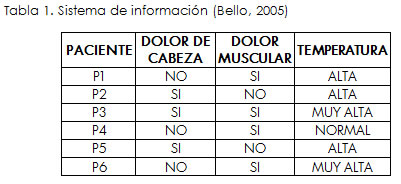
Siguiendo la teoría de los conjuntos aproximados, un sistema de información está compuesto por atributos y elementos, donde cada atributo contiene un valor cualitativo o cuantitativo para cada elemento (Bello, 2005), (Wang et ál., 2003).
Sea un conjunto de atributos 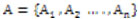 y un conjunto
y un conjunto 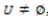 , "Universo de ejemplos" (objetos, entidades, situaciones o estados, etc.) descritos utilizando los atributos Ai . Al par (U, A) se le denomina sistema de información, que puede expresase como una pareja ordenada {(objeto, situación, entidades), atributo}. Ejemplo:
, "Universo de ejemplos" (objetos, entidades, situaciones o estados, etc.) descritos utilizando los atributos Ai . Al par (U, A) se le denomina sistema de información, que puede expresase como una pareja ordenada {(objeto, situación, entidades), atributo}. Ejemplo:
Un sistema de decisión es un sistema de información más un nuevo atributo "d", llamado decisión (Bello, 2005); éste indica la decisión tomada en ese estado o en esa situación; entonces, se obtiene un sistema de decisión:
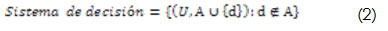
El "valor de la decisión" puede representar un valor cualitativo o cuantitativo con el cual se clasifica el objeto. Con el atributo de decisión "d" es posible realizar una clasificación del universo de objetos U. Sea el conjunto Vd = {1,…m} un conjunto de enteros, entonces {X1,… Xn} es una colección de clases de equivalencia, llamadas clases de decisión, en donde dos objetos pertenecen a la misma clase si tienen el mismo valor para el atributo decisión:
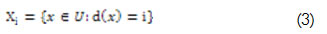
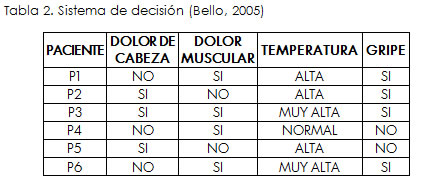
De la *Tabla 2 se obtienen las clases de decisión (conjunto X), para ello se obtiene el valor de la decisión de cada elemento (Pi):
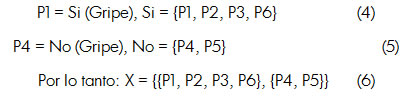
Relación de inseparabilidad
El concepto de inseparabilidad es muy importante en la teoría de los conjuntos aproximados; para explicar este concepto se toman varios elementos de un atributo dado, elementos que pueden distinguirse (diferenciarse) por el valor de dicho atributo: si se eligen dos elementos (x, y), para saber si se distinguen se recurre a la siguiente expresión (Bello, 2005):
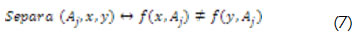
En otras palabras, la inseparabilidad significa que dos elementos son separables si el valor de un atributo dado para ellos es diferente, en caso contrario los elementos son inseparables. Retomando la *Tabla 2 , se puede afirmar que:

Es posible construir una matriz donde se indique la separabilidad en un conjunto:
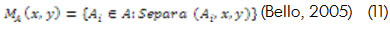
Utilizando la información de la *Tabla 1 es posible construir la siguiente matriz de separabilidad:
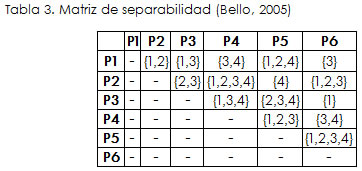
La separabilidad también se puede representar estableciendo una condición menos estricta que la comparación de igualdad o desigualdad de los valores de los atributos; para ello se utilizará una variable (![]() , a la cual se puede asignar un valor determinado (Pawlak, 1991), (Bello, 2005):
, a la cual se puede asignar un valor determinado (Pawlak, 1991), (Bello, 2005):
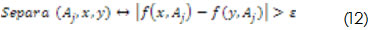
De acuerdo a Pawlak, "A cada subconjunto de atributos B de A 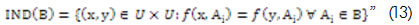 , está asociada una relación binaria de inseparabilidad denotada por IND(B), la cual es el conjunto de pares de objetos que son inseparables uno de otro por esta relación:
, está asociada una relación binaria de inseparabilidad denotada por IND(B), la cual es el conjunto de pares de objetos que son inseparables uno de otro por esta relación:
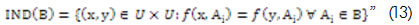
Una relación de inseparabilidad que sea definida a partir de formar subconjuntos de elementos de U (U=Universo) que tienen igual valor para un subconjunto de atributos B de A 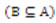 , es una relación de equivalencia que es reflexiva, simétrica y transitiva (Pawlak, 1991).
, es una relación de equivalencia que es reflexiva, simétrica y transitiva (Pawlak, 1991).
Conjuntos aproximados superior e inferiormente
Sea el sistema de información (U, A), (U = Universo, A = Atributos) y los conjuntos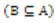 , donde B es un subconjunto de atributos de A y X es un subconjunto de elementos de U. Se puede aproximar X usando solamente la información contenida en B construyendo dos conjuntos llamados Aaproximación Inferior (B*) y Aproximación Superior (B*) del conjunto X para la relación B, así (Pawlak, 1991):
, donde B es un subconjunto de atributos de A y X es un subconjunto de elementos de U. Se puede aproximar X usando solamente la información contenida en B construyendo dos conjuntos llamados Aaproximación Inferior (B*) y Aproximación Superior (B*) del conjunto X para la relación B, así (Pawlak, 1991):
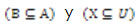
La aproximación inferior de un conjunto (con respecto a un conjunto de atributos dado), se define como la colección de casos cuyas clases de equivalencia están contenidas completamente en el conjunto, mientras que la aproximación superior se define como la colección de casos cuyas clases de equivalencia están al menos parcialmente contenidas en el conjunto, es decir, hay intersección diferente de vacío (Bello, 2005), (Pawlak, 1991). Con base en las aproximaciones inferior y superior es posible estipular medidas para inferir conocimiento desde el sistema de decisión, gracias a unas pautas establecidas sobre tales conceptos, siendo una de ellas la precisión de la clasificación, que se determina según la cantidad de valores de decisión que posea el sistema, la otra se conoce como vaguedad del concepto o conjunto X con respecto a la relación B y se caracteriza matemáticamente por el cociente:
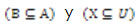
Donde |X| denota la cardinalidad del conjunto X y 0≤cE(X) ≤ 1. Si cE(X)= 1 el conjunto será duro o exacto con respecto a la relación de equivalencia B, mientras que si cE(X)> 1 , el conjunto es aproximado o vago con respecto a B. Se mide así el grado de imperfección o integridad del conocimiento sobre el conjunto X considerando los atributos incluidos en la relación de equivalencia.
Clasificación de imágenes digitales
La clasificación de imágnes es uno de los métodos más utilizados para extracción de información. Desde un enfoque clásico, puede decirse que existen dos variantes fundamentales para la clasificación: supervisada y no supervisada. Muchos algoritmos están disponibles para ambas alternativas (Jensen, 1996).
En la clasificación supervisada se requiere tener datos con clases conocidas por adelantado, comúnmente referidas como conjuntos de entrenamiento, cuyo propósito es entrenar el algoritmo de clasificación. Se calculan parámetros estadísticos como la media, la desviación estándar, las matrices de covarianza, las matrices de correlación, etc, para cada conjunto de entrenamiento. Después del entrenamiento, se dice que el clasificador ha sido entrenado.
En la clasificación no supervisada el computador usa algoritmos para determinar automáticamente la similitud de las firmas espectrales y agrupar posteriormente los pixeles con características espectrales similares, con base en algún criterio estadístico determinado que a su vez se codifica dentro del sofware. Las clasificaciones no supervisadas requieren una interacción mínima con el usuario, esto significa que se proveen el número máximo y mínimo de clases que se esperan del servicio de clasificación.
Servicio web inteligente
La estructura del servicio web inteligente, cuyo código se ha etiquetado con el nombre "WebServiceRoughSets" se muestra en la Figura 1 ; recibe la imagen digital con valores de los niveles digitales correspondientes a los rangos de longitud de onda del espectro electromagnético visible y los valores para la decisión y precisión enviados por el cliente, calcula la inseparabilidad y encuentra las aproximaciones inferior y superior. El diseño del servicio web permite a diversos usuarios realizar este tipo de análisis sobre imágenes digitales, en especial aquellos cuyas máquinas tengan características de hardware pequeñas en procesador y memoria, recursos que serán asumidos por el servidor.
La siguiente figura ilustra la estructura del servicio web:
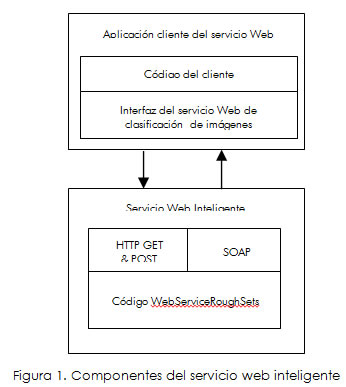
El usuario, mediante una aplicación cliente, realiza la petición al "WebServiceRoughSets"; en primera instancia, de "manera local", selecciona la imagen digital a clasificar, luego indica cuál será el parámetro de "decisión" sobre el que se realizará la clasificación (color), así como la precisión de la misma (grado de semejanza). El cliente envía estos parámetros al servidor, que complementa el ciclo.
La primera tarea: "Enviar la imagen digital al servidor" se logra a través de la "serialización de la imagen digital" y se puede aplicar a los formatos ".bmp, .gif, .png y .jpg". El servidor devuelve los resultados serializando la imagen digital y el cliente la deserializa para visualizar dicho resultado.
El servidor una vez recibe la imagen digital serializada y los parámetros, se encarga del trabajo "pesado" y realiza la deserialización y clasificación a través de un algoritmo basado en la teoría de los conjuntos aproximados y devuelve los resultados al cliente (nuevamente serializa la imagen).
Para realizar la primera clasificación el servidor en primera instancia deserializa la imagen digital y la convierte en un objeto de tipo "bitmap", luego calcula el tamaño en pixeles del bitmap a fin de construir una matriz de pixeles vs. los valores RGB por cada pixel. Una vez se construye la matriz se aplica la teoría de conjuntos aproximados y se encuentran los conjuntos inseparables.
El software del servidor implementa, de manera novedosa, el concepto de precisión aproximada, para ello se utiliza la variable precisión, que ayuda a clasificar la imagen de acuerdo a grados de semejanza que van de 0 al 100%, este valor es definido por el usuario desde el lado "cliente" y se aplica tanto a la inseparabilidad como al cálculo de la decisión. El concepto precisión ayuda a definir a qué subconjunto deberá pertenecer cada pixel a clasificar. La Figura 2 ilustra el proceso computacional seguido para la clasificación de la imagen digital.
El cliente, además de la imagen digital, envía el valor de la decisión que corresponde a un color, entonces el servidor toma los componentes RGB del color de la decisión y aplica el mismo concepto de "precisión". De esta manera se logra determinar a cuál clase de equivalencia pertenece cada pixel, en este caso se tienen valores binarios 1 ó 0, donde uno (1) indica que el pixel contiene el mismo valor de la decisión y formará parte del subconjunto de la "clase de equivalencia Sí" (positiva) o en caso contrario el valor cero (0) significa que formará parte del subconjunto de la "clase de equivalencia No" (negativa).
Para dar solución a la decisión de a dónde enviar un elemento que puede pertenecer a varios subconjuntos, el software construye un grafo, el cual conecta los elementos (pixeles) y asigna como valor de enlace la distancia entre ellos (distancia euclidiana). Una vez se han construido en su totalidad todos los subconjuntos, también se ha generado el grafo completo.
Para la construcción del grafo el algoritmo tiene en cuenta los siguientes pasos:
- Encontrar los conjuntos inseparables, los elementos que forman parte de cada subconjunto no tienen incertidumbre.
- A medida que aparecen elementos con incertidumbre se construye el "grafo", cada nodo corresponde al pixel a clasificar y se asigna como valor de enlace la distancia entre ellos.
- Se recorre el grafo iniciando por la "raíz" y se evalúa la distancia entre cada nodo por todos los enlaces existentes y se procede a clasificar utilizando como criterio la distancia más cercana, es decir, el elemento pertenecerá al enlace con menor distancia, ubicando al elemento en un subconjunto determinado.
- Para el caso de empate en el valor de la distancia de un elemento vs. sus "n" posibilidades de pertenencia a un subconjunto determinado se crearon dos opciones abiertas al usuario:
-Crear conjuntos unitarios: significa que los elementos con incertidumbre formarán conjuntos unitarios.
-Clasificación aleatoria: significa que el sistema elegirá a cuál subconjunto enviará el elemento a clasificar.
Resultados experimentales
Para ilustrar cómo funciona el servicio web diseñado, se presentan a continuación los resultados obtenidos luego de clasificar una imagen digital en formato jpg, con un tamaño de 179 x 178 pixeles.
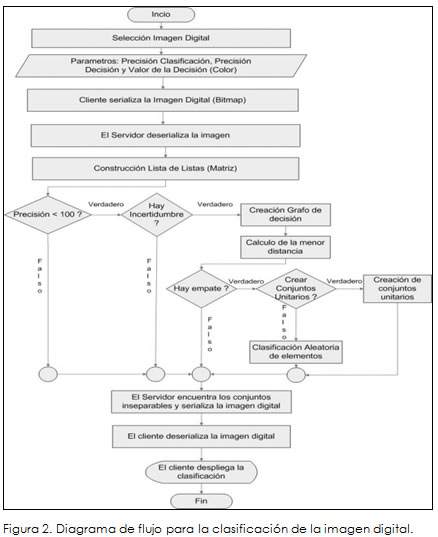
Se configuró el grado de precisión, asignando para la "inseparabilidad" un valor de 100 (los valores pueden ir de 0 a 100, donde 100 significa que el grado de semejanza es absoluta), para la "decisión" se asignó también un valor de 100 (los valores pueden ir de 0 a 100, donde 100 significa igualdad absoluta respecto del color de decisión determinado), para el "color de la decisión" se selec-cionó el rojo (RGB = 255,0,0).
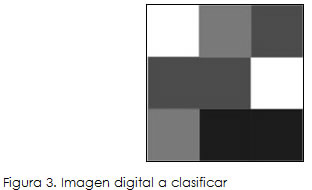
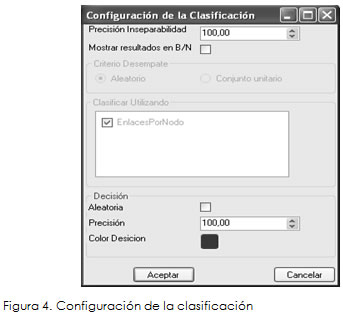
Se ubicó la ventana de clasificación, con un tamaño de 9 x 9 pixeles, tal como lo ilustra la siguiente figura:

El software encontró que la clase de equivalencia positiva, es decir, aquellos pixeles iguales a rojo, a su vez era igual a "vacío"; en otras palabras, ningún pixel dentro de la ventana de clasificación fue "rojo".

En esta área de la ventana, como ningún pixel fue rojo, las aproximaciones superior e inferior para la clase de equivalencia positiva fueron iguales a "vacío" y las imágenes de las aproximaciones resultaron también iguales a la imagen "clase de equivalencia positiva".
El software también encontró la clase de equivalencia negativa, situación que se ilustra en la Figura 7 . Esta clasificación correspondió a toda la "zona de la ventana", lo cual significaba que ningún pixel era rojo.

Por razones de espacio, en la *Tabla 4 se presenta una fracción de los datos correspondientes a los resultados obtenidos de la clasificación de la imagen digital utilizando el servicio web inteligente "WebServiceRoughSets", que a su vez encontró la clase de equivalencia positiva y las aproximaciones inferior y superior respectivas:
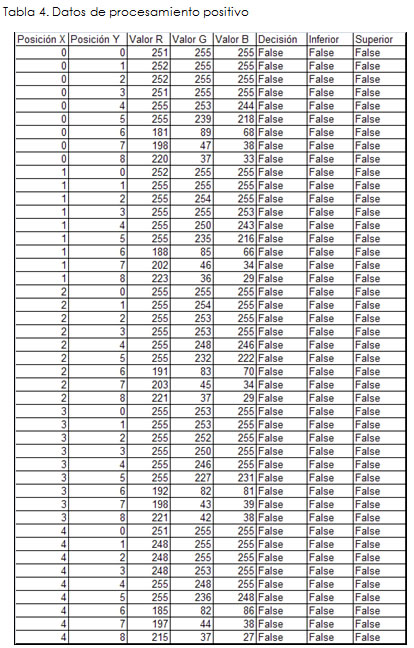
En la *Tabla 5 se presenta una parte de los resultados obtenidos luego de la clasificación de la imagen digital utilizando el servicio web inteligente "WebServiceRoughSets", que también encontró la clase de equivalencia negativa y las aproximaciones inferior y superior respectivas:
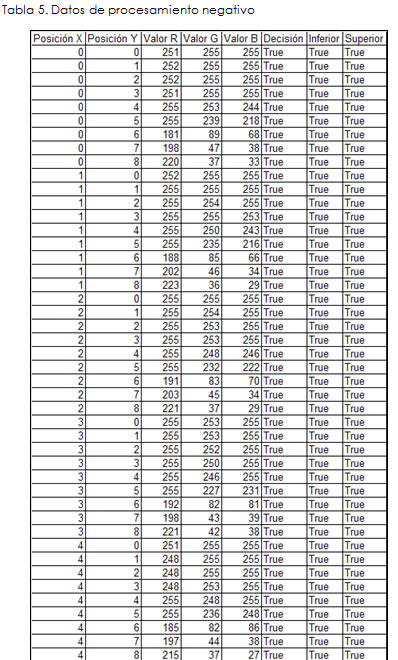
Conclusiones
La teoría de los conjuntos aproximados se utilizó para realizar una clasificación de elementos del universo (aproximación superior, aproximación inferior, clases de equivalencia) a partir de una serie de reglas (inseparabilidad). Se demostró así que la teoría de los conjuntos aproximados es una herramienta válida para realizar clasificación de datos, según los resultados obtenidos con el servicio web inteligente creado.
El servicio web inteligente "WebServiceRoughSets" se basa en la teoría de conjuntos aproximados y puede aplicarse a imágenes digitales en formatos ".bmp, .gif, .png y .jpg", permitiendo prácticas académicas que ilustran de manera didáctica la teoría de Rough Sets propuesta por Pawlak.
El concepto "precisión aproximada", propuesto de manera novedosa por los autores, permitió realizar múltiples combinaciones para el cálculo de inseparabilidad o la decisión, situación que contribuye a disponer de diferentes perspectivas para el análisis de datos.
El trabajo con imágenes digitales implicó el diseño de estrategias para extraer los valores de cada pixel a través de procesos de serialización así como la implementación del algoritmo que conduce a encontrar los conjuntos aproximados. La aplicabilidad de la teoría de los conjuntos aproximados es posible donde exista información facti<ble de ser representada por sistemas de información o sistemas de decisión. La teoría de los conjuntos aproximados es una potente herramienta de análisis y clasificación de la información, elementos esenciales para el descubrimiento del conocimiento en grandes volúmenes de datos.
Para mejorar la calidad de la clasificación puede combinarse la teoría de conjuntos aproximados con otras técnicas, por ejemplo con la capacidad de procesamiento de imágenes de percepción remota multirresolución recurriendo a la teoría de los wavelets (Xia et ál., 2004), con redes neuronales artificiales (Lee et ál., 2002), lógica difusa (Miao et ál., 2005), (Huang et ál., 2003), o reducción de incertidumbre (Pal, 2002), (Pawlak, 1995), (Aldridge, 1998), (Worboys, 2004).
Bibliografía
Aldridge, C., A Theory Of Empirical Spatial Knowledge Supporting Rough Set Based Knowledge Discovery in Geographic Databases., Ph.D. Thesis, University of Otago, Dunedin, New Zealand, 1998. [ Links ]
Bandyopadhyay, S., Satellite image classification using genetically guided fuzzy clustering with spatial information, Int. J. Remote Sens., vol. 26, No. 3, 2005, pp. 579-593. [ Links ]
Bazi, Y., Melgani, F., Toward an optimal svm classification system for hyperspectral remote sensing images, IEEE Transactions on Geoscience and Remote Sensing., Vol. 44, No. 11, Nov., 2006. [ Links ]
Bello, R., Métodos de Solución a los Problemas de Inteligencia Artificial, Conferencia 12: Conjuntos Aproximados Superior e Inferiormente., Departamento de Ciencia de la Computación Universidad Central de Las Villas, Cuba, 2005. [ Links ]
Benediktsson, J. A., Sveinsson, J. R., Feature extraction for multisource data classification with artificial neural networks, Int. J. Remote Sens., Vol. 18, No. 4, Mar., 1997, pp. 727-740. [ Links ]
Cerami, E., Web Services Essentials., Sebastopol, OReilly & Associates., CA, USA., 2002, pp. 288. [ Links ]
Huang, X., Yi, J., Zhang, Y., A method of constructing fuzzy neural network based on rough set theory, Proceedings of the Second International Conference on Machine Learning and Cybernetics, Xi´an, 2-5 November, 2003. [ Links ]
Lee, J., Park, J., Shin, J., Lee, K., A system marginal price forecasting based on an artificial neural network adapted with rough set theory., 2002, En IEEE 0-7803-9156-X-05. [ Links ]
Li, Y., Liu, Y., Wang, X., Lin, H., An initial comparison of fuzzy sets and rough sets from the view of pansystems theory, 2005. En IEEE 0-7803-9017-2/05. [ Links ]
Mannan, B., Roy, J., Ray, A. K., Fuzzy ARTMAP supervised classification of multi-spectral remotely-sensed images., Int. J. Remote Sens., Vol. 19, No. 4, Mar., 1998, pp. 767-774. [ Links ]
Miao, D., Li, D., Fan, S., Fuzzy rough set and its improvement., 2005. En IEEE 0-7803-9017-2/05. [ Links ]
Pal, S., Mitra, P., Multispectral image segmentation using the rough-set-initialized EM algorithm., En IEEE Transactions On Geoscience And Remote Sensing., Vol. 40, No. 11, November. 2002. [ Links ]
Pawlak, Z., Granularity of knowledge, iniscernibility and rough sets., 1988. En IEEE 0-7803-4863-X/98. [ Links ]
Pawlak, Z., Rough sets theorical aspects of reasoning about data, Kluber academic publishers., 1991, pp. 1-43. [ Links ]
Pawlak, Z., Vagueness and uncertainty: a rough set perspective., Computational Intelligence., 1995. [ Links ]
Pawlak, Z., Grzymala-Busse, J., Slowinski, R., Ziarko, W. Rough Sets. Communications of the ACM, ABI/INFORM Global., Vol 38, No. 11, 1995. [ Links ]
Peters, J. F., Pawlak, Z., Skowron A., A rough set approach to measuring information granules., Proceedings of the 26 th Annual International Computer Software and Applications Conference., 2002. [ Links ]
UDDI., http://www.uddi.org/pubs/uddi_v3.htm 2000. (Consulta: 29.03.2010), 2010. [ Links ]
Wang, Q., Wang, X., Zhao, M., Wang, D., Conceptual hierarchy based rough set model., Proceedings of the Second International Conference on Machine Learning and Cybernetics, Xian., 2-5 Nov., 2003. [ Links ]
Worboys, M., Duckham, M., GIS a Computing perspective., Second Edition., CRC Press, 2004. [ Links ]
World Wide Web Consortium., Web Service Architecture, W3C Working Group Note February 11th 2004. http://www.w3c.org/TR/ws-arch/ (Consulta: 28.03.2010). 2010. [ Links ]
Xia, M., He, Y., Huang, X., Su, F., Image fusion algorithm using rough sets theory and wavelet analisis., 2004, En IEEE 0-7803-8406-7/04. [ Links ]
Xu, X., Peters, J., Rough set methods in power system fault classification., Proceedings of the Canadian Conference on Electrical & Computer Engineering., 2002. [ Links ]
Zhang, Y., Lin T. Y., Computational Web Intelligence (CWI): Synergy of Computational Intelligence and Web Techonology., Fuzz-IEEE02., Proceedings of the IEEE International Conference on Fuzzy Systems., 2002. [ Links ]














