Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.30 no.1 Bogotá Apr. 2010
Fredy Andrés Olarte Dussán1,Carlos Eduardo Borda Zapata2, y Hernando Díaz Morales3
1Ingeniero electrónico, Universidad Distrital Francisco José de Caldas, Colombia. M.Sc., Magister en Automatización Industrial, Universidad Nacional de Colombia, Bogotá. Profesor Auxiliar, Universidad Nacional de Colombia, Facultad de Ingeniería, Departamento de Ingeniería Eléctrica y Electrónica, Bogotá. faolarted@unal.edu.co .2Ingeniero electricista, Universidad Nacional de Colombia, Bogotá. M.Sc., en Ingeniería Eléctrica, Universidad Nacional de Colombia, Bogotá. Vinculado a XM, Medellín, Colombia. cborda@xm.com.co 3Ingeniero electricista. M.Sc., Electric Power Engineering, Rensselaer Polytechnic Institute, Estados Unidos. Ph.D., Electrical Engineering, Rensselaer Polytechnic Institute, Estados Unidos. Profesor titular, Universidad Nacional de Colombia, Facultad de Ingeniería, Departamento de Ingeniería Eléctrica y Electrónica.hdiazmo@unal.edu.co
RESUMEN
Este artículo presenta dos algoritmos, basados en estimación de estado, para la identificación de parámetros de líneas de transmisión. Las técnicas utilizadas se fundamentan en la inclusión de los parámetros de las líneas en el vector de estado y la solución del estimador de estado por mínimos cuadrados ponderados. En ambos casos se construyerón sistemas de potencia ficticios que se componen de copias de la misma línea de transmisión para diferentes instantes de tiempo. Uno de los algoritmos usó mediciones de magnitud de voltaje y potencia activa y reactiva, mientras que el otro implementó mediciones fasoriales sincronizadas de voltaje y corriente. Los algoritmos fueron evaluados utilizando mediciones simuladas en el sistema de 30 nodos de IEEE. Ambas soluciones identificaron la totalidad de los parámetros de las líneas con errores menores del 1%.
Palabras clave: estimación de estado, estimación de parámetros, PMU, mínimos cuadrados.
ABSTRACT
This article presents two state-estimation-based algorithms for identifying transmission line parameters. The identification technique used simultaneous state-parameter estimation on an artificial power system composed of several copies of the same transmission line, using measurements at different points in time. The first algorithm used active and reactive power measurements at both ends of the line. The second method used synchronised phasor voltage and current measurements at both ends. The algorithms were tested in simulated conditions on the 30-node IEEE test system. All line parameters for this system were estimated with errors below 1%.
Keywords: state estimation, parameter estimation, PMU, least squares.
Recibido: abril 14 de 2009 Aceptado: febrero 10 de 2010
Introducción
A partir de ese momento un gran esfuerzo investigativo se ha enfocado en solucionar los problemas inherentes al proceso de estimación, como la detección y eliminación de errores sistemáticos, el aumento en la velocidad de procesamiento el uso de condiciones del sistema para aumentar la confiabilidad de los resultados, entre otros, Abur y Celik, 1991; Abur y Celik, 1995; Aschmoneit et ál., 1997; Korres, 2002; Kotiuga y Vidyasagar, 1982; Singhand et ál., 1997; Singh y Alvarado, 1994; Zhang et ál., 1992. No obstante, un problema básico para cualquier tipo de estimador es la necesidad de fijar valores para los parámetros del modelo p de la red de potencia. Con el fin de solucionar las ecuaciones del estimador se deben suponer valores exactos de estos parámetros para cada una de las líneas que componen el sistema de potencia. En la realidad esta condición muy difícilmente se cumple (Al-Othman y Irving, 2005; Van-Cutsem y Quintana, 1988; Kusic y Garrison, 2004; Meliopoulos et ál., 2001; Zarco y Exposito, 2000).
La estimación de parámetros es el proceso mediante el cual uno o varios parámetros de la red de los cuales se sospecha sobre su precisión se valoran a partir de otras mediciones. La estimación de parámetros es importante debido a que valores más precisos en los parámetros conducen a mejores resultados en el SE y en aplicaciones como análisis de seguridad, despacho económico y flujo de carga óptimo (Kusic y Garrison, 2004). Es un hecho común que las bases de datos de los parámetros con que cuentan las empresas tengan errores significativamente grandes debido a imprecisión de los datos reportados por los fabricantes, modificación de los circuítos sin actualizar la base de datos, al desgaste de los materiales o cambios en las condiciones ideales con las cuales se calculó el modelo p (Alsac et ál., 1998; Meliopoulos et ál., 2001; Zarco y Exposito, 2000). Según Kusic (Kusic y Garrison, 2004), los errores en los parámetros debido a las desviaciones de los valores ideales de cálculo para una línea suelen estar entre un 25% y un 30%. El PE (Parameter Estimator) permite actualizar la base de datos y rastrear cambios de los parámetros a lo largo del tiempo, ya sean lentos debido al desgaste normal de los materiales, o rápidos, como los relacionados con el efecto corona (Alsac et ál., 1998) o compensación serie.
La estimación de parámetros generalmente se desarrolla mediante dos metodologías. La primera ejecuta el PE posterior al SE (VanCutsem y Quintana, 1988; Liu et ál., 1992), lo cual le da la ventaja de que el código principal del SE no es modificado. Una vez obtenido el resultado del SE, se analizan todos los residuos de las medidas, seleccionando aquellas mediciones que presentan los mayores residuos. Dado que el proceso de la estimación de parámetros es un problema local (Zarco y Exposito, 2000), se seleccionan las líneas cercanas al punto en donde se presentaron los residuos de las medidas más altos. Por medio de la relación lineal que existe entre los residuos de las medidas y los errores en los parámetros, y por medio de la matriz de sensibilidad del error, se hallan los errores de los parámetros y se actualizan sus valores. Las diferencias entre los distintos métodos de este tipo está en la formación del vector de errores (Zarco y Exposito, 2000).
La segunda metodología ejecuta el PE al mismo tiempo que el SE, como es el caso de los métodos basados en el aumento del vector de estado (Liu y Lim, 1995; Zhong y Abur, 2005; Zhu y Abur, 2006). Estos métodos aumentan el vector de estado al agregarle como estados adicionales a estimar un número Np de parámetros que se sospechan erróneos. Se han propuesto varias formas de solución. La más común utiliza las ecuaciones normales del estimador de estado por mínimos cuadrados ponderados (WLS, Weighted Least Square), como un caso particular del criterio de máxima verosimilitud (ML, Maximum Likelihood), en donde se asume que la función de densidad de los errores es normal (Alsac et ál., 1998; Meliopoulos et ál., 2001). Otra forma de solucionar la estimación de parámetros con el vector aumentado es por medio de la teoría del filtro Kalman en el estimador por WLS, el cual usa diversos conjuntos de mediciones. El uso de la teoría del filtro Kalman es un método recursivo que va estimando los parámetros del sistema a medida que se añade un nuevo conjunto de mediciones, es decir, partiendo de un conjunto de mediciones dadas, el estimador basado en la teoría de Kalman estima los parámetros del sistema y sus respectivos valores de covarianza. En la estimación subsecuente k+1, el valor de los parámetros hallados en k, se utilizan como pseudo medidas y su covarianza es la hallada en la estimación k (Debs, 1974). Dicha técnica para la estimación de parámetros tiene en cuenta la variación que éstos tienen en función del tiempo.
Sin importar cuál de las dos metodologías descritas para el estimación de parámetros se use, la solución se deteriora a medida que se estima una mayor cantidad de parámetros (Zarco y Exposito, 2000). En Olarte y Diaz (2008) se propone una nueva metodología capaz de estimar los parámetros de todas las líneas de una red sin que se deteriore la solución. Ésta se basa en la solución de un estimador combinado de estados y parámetros, de mínimos cuadrados ponderados, aplicado a un sistema ficticio en donde todas las líneas comparten los mismos parámetros del modelo p. Por otra parte, las PMU (Phasor Measurement Units) fueron introducidas a mediados de los años ochenta; estos instrumentos miden en forma sincronizada los fasores de secuencia positiva de tensión de un nodo y los fasores de secuencia positiva de las corrientes de las líneas conectadas a él La sincronización de las medidas se logra utilizando el sistema de posicionamiento global (GPS). El primer proto-tipo de PMU se construyó en Virginia Tech, tomando como base el desarrollo previo que se había hecho en los años setenta del relé de distancia de componentes simétricas (Phadke, 2002).
Desde su aparición, la principal aplicación que se pensó para las PMU fue la estimación de estado (Phadke, 2002). Trabajos reciéntes (Zhou et ál., 2006) han mostrado que la precisión de la estimación de estado aumenta si se incluyen junto con las mediciones tradicionales de potencia y tensión, mediciones fasoriales sincronizadas. Es un hecho la tendencia creciente de instalación de unidades de medición fasorial (Huang y Dagle, 2008), de continuar así se espera en un futuro tener mediciones fasoriales de tensión en la mayoría los nodos de un sistema, lo cual conduciría a un cambio en el proceso de estimación de estado. Pensando en esta aplicación, los trabajos de investigación recientes se enfocan en establecer la ubicación óptima de PMU para mejorar la observabilidad de la red y la detección de datos erróneos (Chen y Abur, 2006; Xu y Abur, 2004). Pero el espectro de posibilidades de investigación con PMU es amplio; existen aplicaciones para medición de frecuencia, predictor de estabilidad de ángulo y tensión, protecciones adaptativas y mejoramiento de control, entre otras (Uhlen et ál., 2008; Le et ál., 2008; Xue, 2008). Adicionalmente, la precisión de estos dispositivos es en muchos casos superior a la alcanzada por los elementos tradicionales de medición de voltaje y potencia (Komarnicki et ál., 2008). Estas características hacen interesante el uso de mediciones fasoriales en la estimación de parámetros.
Este artículo está organizado así: inicialmente se presenta la solución de la estimación de estado por norma mínima. Posteriormente se expone la estimación simultánea de estados y parámetros, se exhibe los algoritmos de estimación de parámetros desarrollados y se ofrece algunos resultados de simulación. Finalmente, se exponen algunas conclusiones.
Estimación de estado por minimización de la norma
ón de estado puede formularse como un problema de minimización de la norma en un espacio vectorial dimensional. Dado un conjunto de mediciones z ∈ Rm, relacionadas con las variables de estado x ∈ Rnpor:
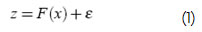
donde F es alguna función no lineal y e es un término que representa el error de medición. El problema de estimación de estado puede definirse como en Boyd (2004):
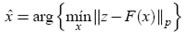
donde 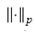 es cualquier norma fija en Rm.
es cualquier norma fija en Rm.
Esta formulación incluye los problemas de estimación más comunes; ejemplo, si la norma es la norma euclidiana usual,
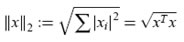
entonces el problema de norma mínima se convierte en el problema de mínimos cuadrados (least square, LS). El problema de mínimos cuadrados ponderados (weighted least square, WLS) puede plantearse en esta forma también:
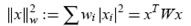
donde W es una matriz diagonal cuyos términos Wii dan pesos wi para la i-ésima medición.
El estimador por valor absoluto ponderado (weighted least absolute value, WLAV), otro método usado en sistemas de potencia, minimiza la siguiente función objetivo:
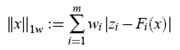
Este estimador puede además representarse como un problema de norma mínima, usando la norma uno. La formulación de norma mínima deja a un lado las preguntas acerca de la distribución de probabilidad de los errores de medición. Dado que el ruido y las características del error son muy pocas veces conocidas, este planteamiento del problema de estimación puede ser de gran valor práctico.
Solución de la estimación de estado por norma mínima
La solución del problema de estimación de estado se obtiene (Alsac et ál., 1998) a través de un proceso iterativo en el cual se busca una solución del problema de estimación de estado no lineal a través de una sucesión de subproblemas lineales. Éste es un procedimiento bien establecido (Schweppe y Handschin, 1974).
Estimación de estado en sistemas de potencia
El problema de estimación de estado en sistemas de potencia puede definirse como:
Dado un conjunto de mediciones que incluyen:
-Mediciones nodales: magnitud de voltajes VkM e inyecciones de potencia activa y reactiva Pk, Qk para el nodo k.
-Mediciones de líneas y transformadores: flujos de potencia activa y reactiva Pi j, Pji, Qi j y Qji para un elemento conectado entre i y j.
y un vector de estado que incluye magnitud de voltajes en nodos Vky ángulos de fase fk para el nodo k, encontrar los componentes del vector de estado que minimizan la norma del error. En este caso, el modelo matemático que relaciona los valores medidos y los calculados está dado por las ecuaciones de flujo e inyección de potencia en las líneas (Arrillaga y Arnold, 1990; Saadat, 1999).
Estimación simultánea de estados y parámetros
Una metodología ampliamente utilizada es la estimación simultánea de estados y parámetros por medio del aumento del vector de estado. Si se cuenta con suficientes mediciones, algunos parámetros se pueden incluir en el vector de estado. El modelo empleado en esta metodología es el siguiente:

En donde z es el vector de mediciones, F es un vector de funciones que relaciona los estados x y los parámetros p con las mediciones y e es el vector de error en las mediciones. Los valores estimados de x y de p se obtienen usando la siguiente expresión:
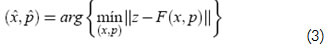
A medida que el número de parámetros incluidos en el vector de estado aumenta, la convergencia del proceso se deteriora, por lo cual se deben escoger con anterioridad los parámetros que se deseen estimar. Una forma de hacerlo es por medio del residuo de las mediciones en la estimación clásica, ya que en términos del SE los errores en los parámetros tienen el mismo efecto que un error de medición. Así por ejemplo, los estimados de las mediciones relacionados con alguna línea van a presentar un residuo menor si los parámetros son correctos. Lo anterior se puede ver en la siguiente ecuación, en donde se ha hecho una manipulación simple de la ecuación (2) teniendo en cuenta el valor verdadero de los parámetros y el valor de los parámetros utilizado en la estimación:
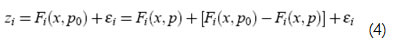
En donde z, F, x y e tienen el mismo significado explicado anteriormente, p es el valor verdadero de los parámetros, p0 es el valor erróneo de los parámetros utilizado en la estimación de estado y el subíndice i representa la i-ésima medición. El término entre los corchetes cuadrados actúa como un error adicional en la i-ésima medición cuando la diferencia entre p y p0 es notable.
El proceso de estimación puede resumirse en el siguiente algoritmo:

Algoritmos propuestos
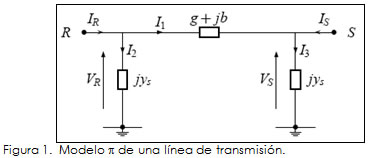
En esta sección se describen los algoritmos para la estimación de los parámetros de líneas de transmisión. La diferencia principal entre los algoritmos radica en las mediciones que utilizan. El primer álgoritmo utiliza potencias activas y reactivas y el segundo se vale de mediciones fasoriales. Los dos algoritmos propuestos identifican los parámetros de una línea de transmisión aumentando el vector de estado y solucionando por WLS. El vector de estado se aumenta con los tres parámetros del modelo p de la línea, r, x y ys. Por simplicidad en los cálculos en el modelo se utiliza la admitancia serie en lugar de la impedancia serie (Figura 1); al final del proceso se calcula el valor de la impedancia serie estimada.
Identificación de parámetros usando mediciones de potencia
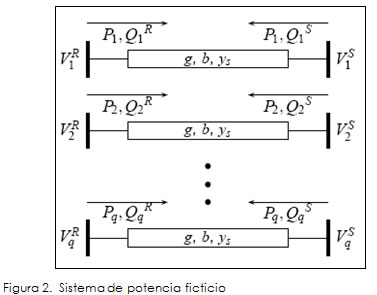
El algoritmo aprovecha la gran cantidad de datos de potencia y tensiones que en un sistema de potencia se pueden obtener en los extremos de un mismo elemento (línea o transformador) en diversos instantes. En cada tiempo se forma un grupo de seis mediciones, dos correspondientes a magnitud de tensión en los extremos del elemento, dos a flujo de potencia activa desde un extremo hacia el otro extremo del elemento, y las dos últimas al flujo de potencia reactiva desde un extremo hacia el otro. Con estas mediciones se construye el sistema ficticio de la Figura 2, el cual consta de q elementos, en donde cada uno corresponde a un conjunto de seis mediciones tomadas en instantes diferentes. El sistema de potencia mostrado es ficticio dado que es una composición de la misma línea q veces, además se supone que los parámetros son constantes. Por otra parte, en este sistema ficticio se ha forzado a que el ángulo de la tensión en todos los nodos R sea cero, ya que no se necesita encontrar los valores reales de las fases sino la diferencia angular entre los nodos. El resultado de la estimación de estado es un vector que contiene los tres parámetros y valores de las magnitudes y las fases del sistema, que sólo se tienen en cuenta para verificar la convergencia. Sin embargo, el resultado de la identificación puede contener un nivel significativo de error, por tanto se propone un proceso de remuestreo que reduce el error a valores típicamente menores al 1%. La idea es repetir la estimación de parámetros tomando datos de forma aleatoria a partir de valores históricos de las mediciones. Por último, se halla el promedio de los parámetros estimados.
Las ecuaciones que relacionan las mediciones (magnitudes de voltaje y potencias) con las variables de estado y los parámetros de una línea de transmisión se muestran a continuación, ecuaciones 5-11:
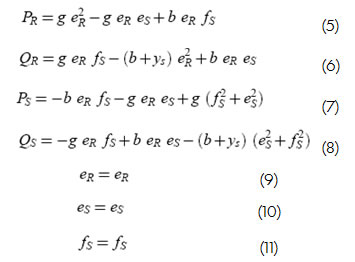
En donde e representa la parte real de las tensiones y f la parte imaginaria éstas. Con q conjuntos de mediciones se tendrían en total 6q ecuaciones que correspondenal sistema de potencia ficticio.
Mediciones fasoriales sincronizadas
Al emplear mediciones fasoriales sincronizadas se obtienen las partes reales e imaginarias de las tensiones en los extremos de cada línea y las corrientes que fluyen desde cada uno de los extremos hacia el otro, también en su parte real e imaginaria. En total se tiene un conjunto de siete mediciones por fracciónde tiempo en una línea de transmisión, cuatro mediciones correspondientes a corriente (parte real e imaginaria de dos corrientes) y tres mediciones correspondientes a tensión (parte real e imaginaria de una tensión y parte real de la otra tensión, pues se ha forzado la tensión del extremo R a tener ángulo cero).
Para q fracciones de tiempo se tiene un total de 7q medidas y se requiere estimar tres parámetros y 3q variables de estado. Esto, dado que los parámetros son los mismos para los q elementos, pero al añadir un nuevo conjunto de medidas, se añade un conjunto de tres variables de estado nuevas a estimar. Al igual que para el algoritmo basado en mediciones de potencia, en este proceso las variables de estado estimadas sólo sirven para verificar convergencia y asegurar un adecuado significado físico de las tensiones.
En coordenadas rectangulares, las ecuaciones que relacionan las variables de estado y los parámetros con las mediciones para una línea de transmisión se obtienen a continuación. De la figura (1) se puede deducir que:
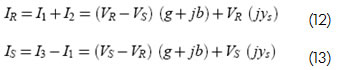
las cuales se pueden separar en parte real e imaginaria, como se muestra a continuación:
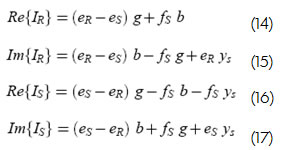
Por último, se presentan las ecuaciones que relacionan las variables de estado con ellas:
en donde e representa la parte real de las tensiones y f la parte imaginaria de éstes. El conjunto de ecuaciones (14)-(20), es el modelo matemático que representa una sola línea de transmisión. Si se tienen q conjuntos de mediciones, es decir q líneas de transmisión ficticias, se tendrán 7q ecuaciones en el modelo.
Resultados
El rendimiento del algoritmo propuesto se verificó a través de simulaciones sobre el sistema de prueba de 30 nodos de la IEEE. Se estimaron todos los parámetros de líneas del sistema. Las mediciones se simularon al adicionar señales de ruido a los valores exactos de los resultados del flujo de carga. Las señales de ruido que se añadieron fueron de dos tipos; la primera, de distribución normal, con el 95% de las mediciones de +- 0,5% del valor exacto, para simular un instrumento de medición clase 0,5, la segunda, una con una distribución uniforme de +-0,5% del valor exacto. La distribución del error que se añade a los resultados no tuvo influencia representativa en el resultado final. Se simularon distintas condiciones de carga para darle variabilidad a los conjuntos de datos. Por cada simulación realizada de una condición de carga se almacenaron potencias activas y reactivas, magnitud de tensión y fasores de tensiones y corrientes en ambos extremos de la línea.
Algoritmo con mediciones de potencia
Para mejorar los resultados de la estimación se utilizó el esquema de remuestreo, igual al que se propuso en (Olarte y Díaz, 2008) en el cual para un mismo elemento se hicieron 1.000 estimaciones de los valores de los parámetros. En cada estimación se construyeron conjuntos aleatorios de 25 datos (q = 25), el resultado fue almacenado. Al cabo de las 1.000 simulaciones el valor estimado final del parámetro se obtuvo como el promedio de las 1.000 estimaciones individuales. La precisión de los valores de los parámetros estimados con este esquema es más alta que con una sola estimación, aun si tienen varios conjuntos de datos. El tiempo de ejecución de todo el proceso de estimación con remuestreo fue de sólo algunos segundos. Toda la programación fue hecha en MATLAB.
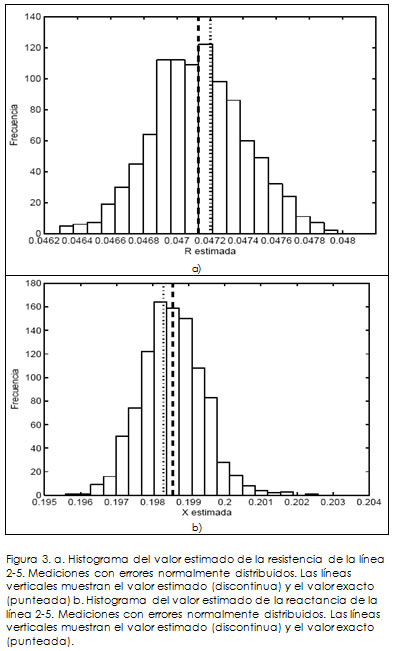
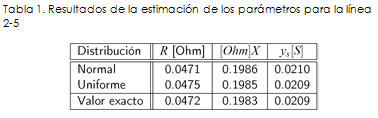
En la Figura 3 se pueden ver los histogramas de los valores estimados de los parámetros R y X de la línea de transmisión que conecta los nodos 2 a 5 del sistema de prueba IEEE de 30 nodos; en los histogramas se aprecia que los valores estimados son muy cercanos a los reales. En la Tabla1 se observa que no hay gran diferencia entre los valores estimados dependiendo de si el error que se añade a las mediciones es normalmente ouniformemente distribuido. Para las restantes líneas se lograron estimaciones en el valor de las reactancias en todos los casos por debajo del 1%. La susceptancia tuvo un error máximo del 5% y la resistencia del 3%.
Algoritmo con mediciones fasoriales
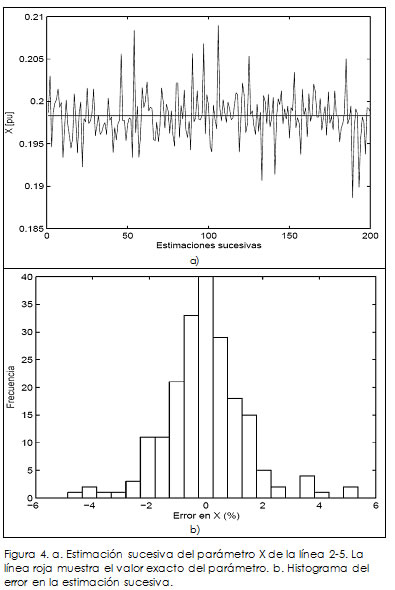
La primera prueba consistió en hacer estimaciones sucesivas con un solo conjunto de mediciones (q = 1) para simular una estima-ción en tiempo real. En la Figura 4a se observa el resultado de esta prueba, en donde se puede apreciar la variabilidad del valor estimado del parámetro X de la línea 2-5 al compararlo con el valor exacto representado por la línea roja. De lo anterior se concluye que no se obtiene buena precisión en el valor estimado del parámetro con un solo conjunto de mediciones. En la Figura 4b. se muestra un histograma del error en porcentaje de las estimaciones sucesivas del parámetro X de la línea 2-5, en la cual se observa claramente que el error toma valores hasta del 5%.
Ahora, si se toman conjuntos de tres mediciones, se obtienen los resultados señalados en la Figura 5. Claramente, el error de la estimación se reduce.
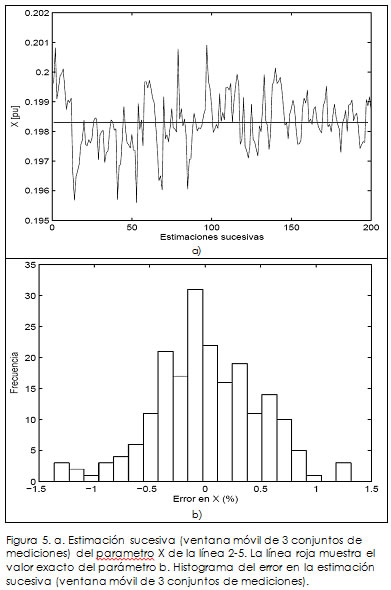
Por lo tanto, tomando más conjuntos de datos para la estimación, los errores de los valores estimados se minimizan.
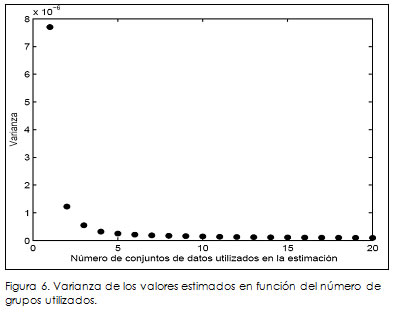
La gráfica 6 muestra la varianza de los valores estimados en función del número de conjuntos de datos utilizados. Se puede ver que la varianza no cambia significativamente tomando más de seis conjuntos de mediciones, abriendo posibilidades a la estimación en línea de parámetros. Para mejorar los resultados de la esti-mación se utilizó el mismo esquema de remuestreo expuesto. La precisión de los valores de los parámetros estimados con este es-quema es más alta que con una sola estimación, aun si se tienen varios conjuntos de datos. El tiempo de ejecución de todo el pro-ceso de estimación con remuestreo fue de solo algunos segundos en un computador de 1,8 GHz.
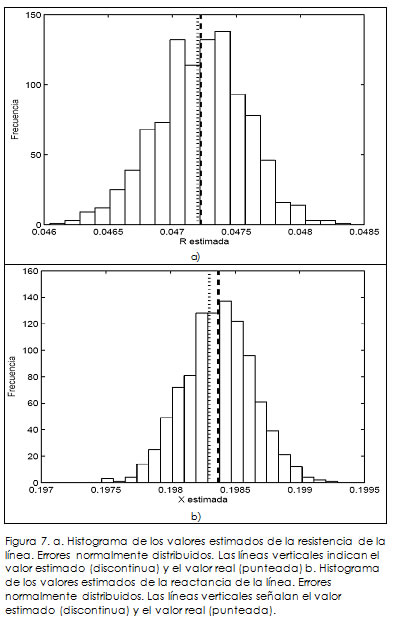
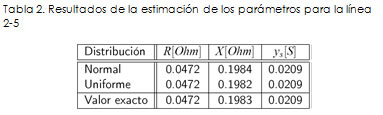
En los resultados de la estimación en las líneas de transmisión, la mayoría de los errores promedio de la estimación de la reactancia X estuvieron por debajo de 1%, excepto para la línea 21−22, el cual presentó un error promedio de 17,74%. Este considerable margen en esa línea se debe a que los parámetros de ella son muy pequeños comparados con las demás, por tanto, una pequeña variación del valor del parámetro representa una alta variación en el porcentaje de error. En la estimación de los parámetros de la resistencia y de la suceptancia en paralelo, en la mayoría de los casos el error promedio no supera el 4%. Como ejemplo se muestran los resultados para la estimación de los parámetros R y X de la línea que une los nodos 2 y 5; se tuvo en cuenta un error con distribución normal. La Figura 7 muestra los histogramas para el valor estimado de los parámetros R y X. En estos dos casos, el valor estimado es muy cercano al valor real. En la Tabla 2 se resume la estimación de los parámetros de la línea 2-5. Aquí se puede apreciar la precisión de los valores estimados al compararlos con los valores reales.
Conclusiones
Se desarrollaron dos algoritmos de estimación de parámetros de líneas de transmisión. Estos algoritmos no tienen problemas unméricos si el número de parámetros a estimar aumenta, ya que trata la estimación de parámetros como un problema local. Los algoritmos se diferencian en el tipo de mediciones con las cuales se va a hacer la estimación (mediciones convencionales de potencia y magnitud de tensión o mediciones fasoriales sincronizadas de tensiones y corrientes). Los algoritmos resuelven por mínimos cuadrados el problema de estimación simultánea de estados y parámetros de un sistema de potencia ficticio formado por q copias de la línea de transmisión, en donde cada copia corresponde a un conjunto de mediciones en una fracción de tiempo determinado. Los algoritmos se probaron usando mediciones del sistema de prueba IEEE de 30 nodos, las medidas fueron simuladas añadiendo errores normalmente y uniformemente distribuidos al resultado exacto de flujo de carga. Los resultados de la estimación de parámetros son prácticamente los mismos al comparar los resultados de ambas dis-tribuciones de error en las mediciones.
En el algoritmo basado en mediciones fasoriales sincronizadas se encontró que en la mayoría de casos los parámetros pueden ser estimados con buena precisión mediante un pequeño número de conjuntos de datos. Esto abre la posibilidad de tener estimación de parámetros en tiempo real. Se halló también que una ventana móvil de q ≥ 6, en la mayoría de los casos, era suficiente para hacer una estimación secuencial de parámetros de las líneas de transmisión. En el algoritmo basado en mediciones de potencia se hizo necesario implementar el esquema de remuestreo para mejorar los valores estimados de parámetros constantes. En todos los casos, el esquema de remuestreo puede ser usado para estimar los parámetros con alta precisión.
Al comparar el algoritmo basado en mediciones fasoriales sincronizadas con el que usa mediciones de potencia, se evidenció que la razón de redundancia es mayor usando mediciones fasoriales, ya que ahora se tiene una medición para el ángulo de la tensión. Con esta razón de redundancia mayor, se pueden utilizar menos conjuntos de datos en la estimación y aun así obtener buenos resultados.
Para el caso del algoritmo basado en mediciones fasoriales puede parecer que el requisito de tener unidades de medición fasorial (PMU) en los dos extremos de la línea es muy estricto. Sin embargo, las PMU se vuelven más competitivas con relés y otras unidades de medición. Los fabricantes de relés además están incorporando capacidades de sincrofasores en sus equipos. Por eso pronto puede set álgo común tener mediciones fasoriales sincronizadas disponibles para la mayoría de los elementos. Actualmente éstas ya están disponibles en subestaciones de transformación equipa-das con PMU. Las estimaciones de parámetros también pueden realizarse con equipos portátiles.
Reconocimientos
Este trabajo se realizó con el patrocinio de Codensa S.A, SENA, Colciencias y la Universidad Nacional de Colombia, mediante el proyecto 1101-426-20639.
Bibliografía
Abur, A., Celik, M. K., A fast algorithm for the weighted least absolute value state estimation., IEEE Transactions on Power Systems, Vol. 6, No. 1, 1991, pp. 1-8. [ Links ]
Al-Othman, A. K., Irving, M. R., Analysis of confidence bounds in power system state estimation with uncertainty in both measurements and parameters., Electric Power Systems Research Elsevier, 1(December), 2005. [ Links ]
Alsac, O., Vempati, N., Stott, B., Monticelli. A., Generalized state estimation., Power Systems, IEEE Transactions on, Vol. 13, No. 3, Aug, 1998, pp. 1069-1075. [ Links ]
Arrillaga, J., Arnold, C. P., Computer Analysis of Power Systems., John Wiley And Sons, 1990. [ Links ]
Aschmoneit, F. C., Peterson, N. M., Adrian, E. C., State estimation with equality constraints., Proc. 10th PICA Conf. Toronto Canada, May 1997, pp. 427-430. [ Links ]
Boyd, S., Convex Optimization. Cambridge University Press, 2004. [ Links ]
Chen, J., Abur. A., Placement of PMUs to enable bad data detection in state estimation., Power Systems, IEEE Transactions on, Vol. 21, No. 4, Nov., 2006, pp. 1608-1615. [ Links ]
Debs, A., Estimation of steady-state power system model parameters., IEEE Power Apparatus and Systems, 93, 1974, pp. 1260-1268. [ Links ]
Huang, Z., Dagle, J., SynchroPhasor measurements: System architecture and performance evaluation in supporting wide-area applications., Power and Energy Society General Meeting - Conversion and Delivery of Electrical Energy in the 21st Century, 2008 IEEE, July, 2008, pp. 1-3. [ Links ]
Komarnicki, P., Dzienis, C., Styczynski, Z. A., Blumschein, J., Centeno, V., Practical experience with PMU system testing and calibration requirements., Power and Energy Society General Meeting IEEE, 2008. [ Links ]
Korres, G., A robust method for equality constrained state estimation., IEEE Transactions on Power Systems, 17, May 2002, pp. 305-314. [ Links ]
Kotiuga, W., Vidyasagar, M., Bad data rejection properties of weighted least absolute value techniques applied to static state estimation., IEEE Transactions on Power Systems, 101(4), 1982, pp. 844-851. [ Links ]
Kusic, G. L., Garrison, D. L., Measurement of transmission line parameters from SCADA data., Power Systems Conference and Exposition, IEEE PES, Vol.1, Oct. 2004, pp. 440-445. [ Links ]
Le, F., Pal, B. C., Cory, B. J., Phasor measurement application for power system voltage stability monitoring., Power and Energy Society General Meeting - Conversion and Delivery of Electrical Energy in the 21st Century, 2008 IEEE, July 2008, pp. 1-8. [ Links ]
Liu, W.-H. E., Lim, S-L., Parameter error identification and estimation in power system state estimation. Power Systems, IEEE Transactions on, Vol. 10, No. 1, Feb., 1995, pp. 200-209. [ Links ]
Liu, W.-H. E., Wu, F. F., Lun, S.-M., Estimation of parameter errors from measurement residuals in state estimation [power systems]. Power Systems, IEEE Transactions on, Vol. 7, No. 1, Feb., 1992, pp. 81-89. [ Links ]
Meliopoulos, A. P. S., Fardanesh, B., Zelingher, S., Power system state estimation: modeling error effects and impact on system operation., System Sciences, 2001. Proceedings of the 34th Annual Hawaii International Conference on, Jan., 2001, pp. 682-690. [ Links ]
Olarte, A., Díaz, H., Transmission lines parameter estimation using state estimation algorithms., Power and Energy Society General Meeting - Conversion and Delivery of Electrical Energy in the 21st Century, 2008 IEEE, July, 2008, pp. 1-7. [ Links ]
Phadke, A. G., Synchronized phasor measurements -A historical overview., Transmission and Distribution Conference and Exhibition 2002: Asia Pacific. IEEE/PES, 1Vol.1, Oct. 2002, pp. 476-479. [ Links ]
Saadat, H., Power System Analysis., Mc Graw Hill, 1999. [ Links ]
Schweppe, F. C., Handschin, E. J., Static state estimation in electric power systems., Proceedings of the IEEE, 62, 1974, pp. 972 - 982. [ Links ]
Singh, H., Alvarado, F. L., Weighted least absolute value state estimation using interior point methods., IEEE Transactions on Power Systems, 9(3), Aug. 1994, pp.1478-1484. [ Links ]
Singhand, H., Alvarado, F. L., Liu, W-H E., Constrained LAV state estimation using penalty functions., IEEE Transactions on Power Systems, Vol. 12, No. 1, Feb., 1997, pp. 383-388. [ Links ]
Uhlen, K., Warland, L., Gjerde, J. O., Breidablik, O., Uusitalo, M., Leirbukt, A. B., Korba. P., Monitoring amplitude, frequency and damping of power system oscillations with pmu measurements., Power and Energy Society General Meeting - Conversion and Delivery of Electrical Energy in the 21st Century, 2008 IEEE, July 2008, pp. 1-7. [ Links ]
Van-Cutsem, T., Quintana, V. H., Network parameter estimation using online data with application to transformer tap position estimation., Generation, Transmission and Distribution [see also IEE Proceedings-Generation, Transmission and Distribution], IEE Proceedings C, 135(1), Jan., 1988, pp. 31-40. [ Links ]
Xu, B., Abur, A., Observability analysis and measurement placement for systems with PMUs. Power Systems Conference and Exposition, 2004., IEEE PES, Vol. 2, Oct., 2004, pp. 943-946. [ Links ]
Xue, Y., Some viewpoints and experiences on wide area measurement systems and wide area control systems., Power and Energy Society General Meeting - Conversion and Delivery of Electrical Energy in the 21st Century, 2008 IEEE, July, 2008, pp. 1-6. [ Links ]
Zarco, P., Exposito, A.G., Power system parameter estimation: a survey. Power Systems, IEEE Transactions on, Vol. 15, No. 1, Feb., 2000, pp. 216-222. [ Links ]
Zhang, B., Wang, S., Xiang, N., A linear recursive bad data identification method with real - time application to power system state estimation., IEEE Trans. Power Syst, 7 (3), Aug., 1992, pp. 1378-1395. [ Links ]
Zhong S., Abur, A., Combined state estimation and measurement calibration., Power Systems, IEEE Transactions on, 20(1), Feb., 2005, pp. 458-465. [ Links ]
Zhou, M., Centeno, V. A., Thorp, J. S., Phadke, A. G., An alternative for including phasor measurements in state estimators., Power Systems, IEEE Transactions on, 21(4), Nov. 2006, pp. 1930-1937. [ Links ]
Zhu, J., Abur, A., Identification of network parameter errors., Power Systems, IEEE Transactions on, 21(2), May., 2006, pp. 586-592. [ Links ]














