Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.30 no.1 Bogotá Apr. 2010
María Rosa Castro1, Marcelo Eduardo Echegaray2 Rosa Ana Rodríguez 3 y Stella Maris Udaquiola4
1 Ingeniera química. Jefe de Trabajos Prácticos, Instituto de Ingeniería Química, Facultad de Ingeniería, Universidad Nacional de San Juan, Argentina. mrcastro@ unsj.edu.ar 2 Ingeniero químico. Jefe de Trabajos Prácticos, Instituto de Ingeniería Química, Facultad de Ingeniería, Universidad Nacional de San Juan, Argentina.mechega@ unsj.edu.ar 3Ingeniera química. M.Sc., en Técnica Ambiental. Ph.D., en Ingeniería. Jefe de Trabajos Prácticos, Instituto de Ingeniería Química, Facultad de Ingeniería, Universidad Nacional de San Juan, Argentina. rrodri@unsj.edu.ar 4 Ph.D., en Ingeniera Química. Profesor Titular Exclusivo, Instituto de Ingeniería Química, Facultad de Ingeniería, Universidad Nacional de San Juan, Argentina. estelaudaquiola@unsj.edu.ar
RESUMEN
En la provincia de San Juan, Argentina, la elaboración del vino es una de las actividades económicas más importantes. Para este tipo de industria, es de fundamental importancia predecir la cantidad de producción en función de la cantidad de materia prima. El objetivo de este trabajo es la obtención de un modelo que relacione los kilogramos de uva molidos con los litros de vino producidos. Dicho modelo se usará para realizar predicciones de valores futuros, puntuales y por intervalos de confianza para un nivel determinado de molienda. A tal fin, se trabajó con datos obtenidos de una bodega ubicada en la provincia de San Juan. En primer lugar, se calculó el coeficiente de correlación muestral y se realizó un diagrama de dispersión, el cual indicó una marcada relación lineal entre los litros de vino obtenidos y los kilogramos de uva molidos. Posteriormente, se adoptaron dos modelos lineales y se efectuó el análisis de varianza, ya que los datos provenían de poblaciones normales con igual varianza. De este análisis se desprendió el modelo más adecuado, el cual fue validado con valores experimentales, obteniendo una buena aproximación de estos.
Palabras clave: industria vitivinícola, modelo probabilístico, regresión lineal.
ABSTRACT
Producing wine is a very important economic activity in the province of San Juan in Argentina; it is therefore most important to predict production regarding the quantity of raw material needed. This work was aimed at obtaining a model relating kilograms of crushed grape to the litres of wine so produced. Such model will be used for predicting precise future values and confidence intervals for determined quantities of crushed grapes. Data from a vineyard in the province of San Juan was thus used in this work. The sampling coefficient of correlation was calculated and a dispersion diagram was then constructed; this indicated a lineal relationship between the litres of wine obtained and the kilograms of crushed grape. Two lineal models were then adopted and variance analysis was carried out because the data came from normal populations having the same variance. The most appropriate model was obtained from this analysis; it was validated with experimental values, a good approach being obtained.
Keywords: wine industry, probabilistic model, lineal regression.
Recibido: junio 6 de 2008 Aceptado: septiembre 14 de 2009
Introducción
En la provincia de San Juan, Argentina, la elaboración del vino es una de las actividades económicas más importantes. El proceso de producción del vino varía enormemente de acuerdo al lugar, la bodega, y la calidad y variedad de vino. Mientras el proceso usual puede ser resumido a una forma simplificada, hay muchas diferencias en este proceso que pueden afectar el vino obtenido, como corrientes requeridas, residuos, tiempo de almacenamiento, energía, requerimientos de limpieza y efectos ambientales asociados. El proceso de vinificación puede dividirse en las operaciones uñitarias que se llevan a cabo durante él. La vendimia es el período en el que la bodega presenta su máximo funcionamiento, llevándose a cabo la cosecha y la molienda de la uva (Chapman, et ál. 2001).
El proceso de elaboración del vino comienza con la recolección de la uva. Ésta se realiza cuando el fruto se encuentra en el estado óptimo de maduración, ya que condiciona la calidad e incluso el tipo de vino. Es muy importante el estado sanitario de la uva y su integridad para evitar fermentaciones prematuras e intercambios entre mosto y raspón, que originarían aromas y gustos no deseados.
El transporte a la bodega se hace en remolques de fácil volcado o en cajas en el menor tiempo posible. El remolque debe ser de acero inoxidable, estar protegido con una lona y provisto de un doble fondo para evitar la maceración del mosto. Las cajas, de una capacidad aproximada de 20 kg de uva cada una, se transportan en el remolque y se descargan manualmente en la bodega. Este sistema evita que la uva se aplaste por su propio peso y que llegue por lo tanto en mejores condiciones a la bodega (Storm, 2001).
Las uvas se descargan en una tolva de acero inoxidable provisto en el fondo de un tornillo sinfín que las conduce hacia la prensa, estrujador o estrujadora - despalilladora.
Con el prensado se extrae el mosto de la uva fresca. Esta operación determinará la calidad del vino. Se persigue obtener el mayor mosto posible aplicando la mínima presión para evitar la rotura de pepitas y raspones que transmitirían sustancias de sabor desagradable al mosto. El prensado se debe ejecutar en el menor tiempo posible para reducir la incorporación de aire.
Es muy común realizar un estrujado antes del prensado para facilitar la extracción del mosto. El estrujado consiste en reventar la uva para liberar el jugo de las células de la pulpa haciéndolas pasar entre dos cilindros muy próximos entre sí que giran en sentido contrario. La distancia entre los dos rodillos debe causar la rotura de las pepitas. Una vez terminado el estrujado de la uva en las máquinas correspondientes, existe una cantidad de mosto libre que se puede separar por simple decantación o mediante máquinas escurridoras. El estrujado debe ser hecho de manera rápida con el fin de limitar la intensidad de los fenómenos de maceración y de oxidación. Después del escurrido, la uva recolectada pasa a las prensas para la separación del mosto que aún le queda. En el caso de no estrujar la uva, se hace un prensado directo, cargando la prensa con uvas enteras.
Posteriormente al prensado, se realiza el sulfitado, que consiste en la adición de dióxido de azufre (SO2). Esta sustancia se agrega para controlar los microorganismos evitando que la fermentación se produzca en forma tumultuosa, inhibiendo el crecimiento de las levaduras no productoras de alcohol y favoreciendo las productoras de él. Además protege el mosto de la oxidación por el oxígeno (O2) del aire, ya que éste desnaturaliza el aroma, destruye el afrutado y oscurece el vino blanco; también ayuda a la clarificación del mosto debido a que el retardo de la fermentación implica que durante este periodo el mosto puede decantar sus materias en suspensión (Oreglia, 1978).
Luego, el mosto obtenido, conteniendo hollejos y pulpa, se vuelca en grandes depósitos de madera o acero inoxidable, donde va fermentando debido a las levaduras, transformando los azúcares en alcohol etílico y otros elementos, además de desprender anhídrido carbónico . A su vez, al encontrarse el mosto en contacto con las partes sólidas de la uva, va extrayendo de éstas el color de los denominados antocianos, taninos, etcétera.
El gas carbónico resultante empuja hacia arriba los hollejos, formando en la parte superior una capa llamada sombrero, la cual se debe ir remojando para que continúe la extracción de color y otros elementos. Para ello se realiza el remontado, consistente en extraer líquido de la parte inferior del depósito mediante una manguera e introducirlo por la parte superior. Además, para que el sombrero no se haga excesivamente compacto, debe ser removido cada cierto tiempo. A esto último se le llama bazuqueo (Storm, 2001).
En función del tipo de vino que se quiera elaborar se hará este proceso con más o menos tiempo, habitualmente de 8 y 12 días, a una temperatura entre 26 a 29°C (Santamaría et ál., 1995; Jolibert, 1991). Posteriormente se realiza el descube, que consiste en trasegar únicamente el líquido a otro depósito. La parte sólida restante está impregnada de mosto y para extraerlo se utilizan prensas que aprietan estas masas hasta casi secarlas. El líquido resultante, denominado vino de prensa, es mucho más rico en color y taninos y no se mezcla con el anterior.
Tras la primera fermentación, se lleva a cabo la fermentación maloláctica, el paso de ácido málico a ácido láctico. Este líquido es mucho más suave y agradable que el anterior, por cuanto el vino gana en finura (Ziraldo, 2002) .
En los vinos nuevos se produce una clarificación espontánea, depositando en el fondo de las cubas "las madres" (lías, fangos). Es aconsejable que estos sedimentos no estén mucho tiempo junto al vino para ir disminuyendo la turbidez. Por esta razón se trasiega el vino a cubas limpias frecuentemente. Este proceso airea el vino, siendo esto conveniente al principio, para ayudar al buen acabado de la fermentación y la estabilización del vino, permitiendo la evaporación de sustancias volátiles resultantes de la fermentación y de gas carbónico. El trasiego también es usado para la homogeneización de vinos entre diferentes cubas con el fin de conseguir uniformidad.
Aunque en el trasegado muchos elementos en suspensión son retirados del vino, otros más ligeros no llegan a decantar por sí solos. Por ello se agregan al vino sustancias coloides que arrastran hacia el fondo impurezas en suspensión (Yair, 1996).
Con la filtración se separa la fase sólida insoluble de la fase líquida, sin modificar las características del vino. Durante la elaboración de éste se van a realizar tres filtraciones, con la misma finalidad de limpieza, pero con diferencia en el desarrollo, características y maquinaria empleada. Las dos primeras, filtración devastadora y filtración abrillantadora, se hacen con un solo filtro de tierras, mientras que la tercera, o filtración amicróbica, con filtro de membrana ( Datz y Kullmann, 2006).
La utilización de frío en la bodega se centra en dos puntos principales: control de la temperatura de fermentación y estabilización del vino por ultrarrefrigeración (Palacios et ál., 2009).
El proceso de embotellado constará de varias etapas: despaletizado de las botellas, lavado, llenado, taponado, capsulado, etiquetado, encartonado y embalado de las botellas en cajas, las cuales se organizan en pallets y se almacenan hasta su expedición.
Los vinos jóvenes son comercializados una vez embotellados; sin embargo, los vinos de crianza y reserva reposan en barricas de madera antes de ser embotellados y etiquetados.
Uno de los desafíos que se presenta en la producción en general, es el de conocer la relación existente entre la cantidad de materia prima utilizada y la cantidad de producto obtenido. Para ello se deben utilizar técnicas estadísticas tales como el análisis de regresión, que nos permitirá explorar la naturaleza de esta relación y obtenerla (Flanzy, 2003).
Teniendo en cuenta lo expuesto es que se planteó como objetivo de este trabajo la modelización e investigación de la relación existente entre dos variables muy importantes que se presentan en el proceso de vinificación: los kilogramos de uva molida frente a litros obtenidos de vino tinto fino. Se trabajó con los datos de cantidades de uva molida y litros de vinos obtenidos, proporcionados por una bodega de gran envergadura ubicada en la provincia de San Juan. Para el procesamiento estadístico de ellos se utilizó el software Statgraphics (Pérez López, 1998). En primer lugar, se calculó el coeficiente de correlación muestral que mide la fuerza de la asociación lineal de las variables y se hizo un diagrama de dispersión, el cual indicó una marcada relación lineal entre los litros obtenidos de vino y kilogramos de uva molidos. Posteriormente, se adoptaron dos modelos lineales y se realizó el análisis de varianza, ya que los datos provenían de poblaciones normales con igual varianza. De este análisis se desprendió el modelo más adecuado, el cual fue validado con valores experimentales.
Análisis estadístico de los datos
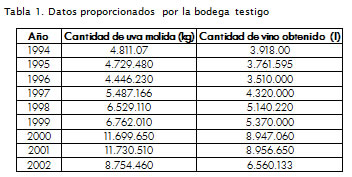
Para llevar a cabo este trabajo, se cuenta con los datos reales de kilogramos de uva molida y litros de vino fino obtenidos en una bodega de nuestro medio, entre los años 1994 a 2002.
Los datos proporcionados por la bodega se presentan en la Tabla 1 . Éstos fueron obtenidos siguiendo el proceso productivo descrito con anterioridad. Para el procesamiento de ellos se optó por el software Statgraphics (Pérez López, 1998), una herramienta utilizada para el procesamiento estadístico de datos ya que permite el análisis de los resultados, su interpretación y la elaboración de conclusiones.
Una estadística descriptiva de los datos sobre kilogramos de uva molidos frente a litros de vino obtenidos, arrojó los resultados des-plegados en la Tabla 2 .
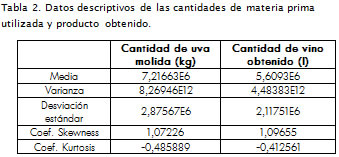
Se puede verificar la suposición de normalidad de las poblaciones comparadas controlando que los coeficientes de forma y apuntamiento se encuentren dentro del rango de valores aceptables (2,2). Del análisis de los coeficientes estandarizados de Skewness y Kurtosis surge el poder considerarse que los datos provienen de poblaciones normales (Box et ál., 2005).
Descripción gráfica de los datos numéricos
En la Figura 1 se ofrecen los diagramas de cajas y bigotes, lo cual da una idea visual sobre la variabilidad de los datos y al no existir algún dato sospechoso que se deba eliminar, para evitar la distorsión de las soluciones obtenidas.
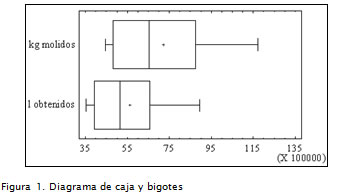
La base de la caja del diagrama se extiende desde el primer cuartil hasta el tercero. La caja representa la mitad central de los datos. La barra vertical que la fracciona en dos partes corresponde a la mediana, y el signo + señala el promedio de los datos (media muestral).
Los bigotes abarcan los datos que apartan como máximo 1,5 veces la diferencia entre el tercer cuartil y el primero (rango intercuartílico). Si algún dato supera estos límites se considera sospechoso y se debería estudiar su procedencia. En este caso en particular como la caja correspondiente a kilogramos molidos es más ancha que la correspondiente a litros obtenidos, indica que los datos de kilogramos molidos están más dispersos que los de litros obtenidos, y como los bigotes del primer diagrama son más largos, que tienen mayor variabilidad.
Además se puede observar en ambos gráfico que como la media está próxima a la mediana y ambas partes de la caja son aproximadamente iguales, los datos presentan simetría con respecto a un valor central.
Coeficiente de correlación muestral
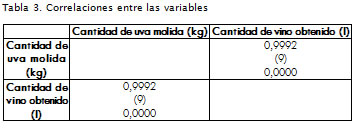
Se comienza el análisis de los datos calculando el coeficiente de correlación muestral, comprendido entre (-1,1) y mide la fuerza de la asociación lineal entre las variables. La Tabla 3 despliega las correlaciones entre las variables. En primer lugar, se puede observar el coeficiente de correlación muestral. Entre paréntesis se indica la cantidad de datos analizados. Debajo de cada coeficiente figura el valor P de la prueba, que establece si la relación encontrada es estadísticamente significativa. Valores P por debajo de 0,05 indican correlación significativa.
Con los datos originales se realiza un diagrama de dispersión (Figura 2); el examen de este diagrama indica que existe una marcada relación entre litros obtenidos y kilogramos molidos, y parece ser razonable la consideración tentativa del modelo lineal.

Elección del modelo
Se ajusta en primer término al modelo lineal (Montgomery et ál., 2004):
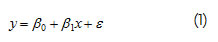
La salida de StatGraphics ofrece el siguiente modelo ajustado (Pérez López, 1998):
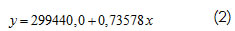
Sin embargo, a pesar de que el modelo en general es adecuado ya que el valor P de la prueba es 0 (Tabla 5 ), y por lo tanto es menor que el nivel de significación 0,05, el coeficiente de correlación es 0,999222, muy cercano a 1, y las pruebas de hipótesis:
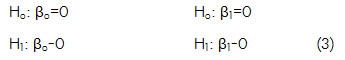
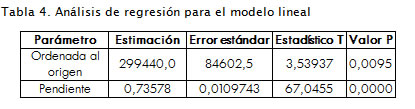
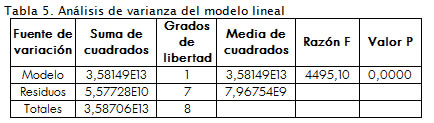
se rechazan (Tabla 4 ), es decir, a nivel poblacional la ordenada al origen y la pendiente de la recta de regresión son distro; el error estándar para la ordenada al origen no es del mismo orden que el error estándar de la pendiente, por lo tanto se decide ajustar a un modelo sin constante.
El modelo sin constante tiene la forma (Montgomery et ál., 2004):

La salida computacional que muestra el modelo ajustado es la siguiente:
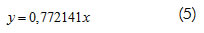
El coeficiente de correlación muestral obtenido es igual a 0,999512.
El análisis de varianza para el ajuste al modelo sin constante arroja un valor P igual a cero, por lo cual se concluye que la regresión es significativa (Tabla 7 ).
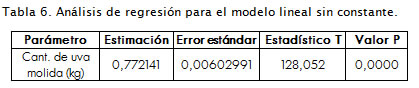
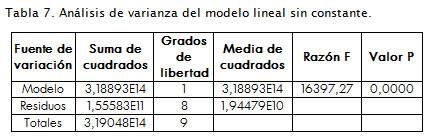
La Tabla 6 contiene la solución obtenida, las estadísticas T y los valores P para la prueba acerca de la significación del coeficiente de regresión β. Se observa que el valor P correspondiente a la prueba para β≠0 es igual a cero, lo que conduce al rechazo de la hipótesis nula Ho: β = 0 con un nivel de significación 0,05.
Un intervalo de confianza al 95% para el coeficiente estimado β, con un error máximo de estimación 0,00602991, es el que figura a continuación (0,758236, 0,786046).
Discusión
Comparando los parámetros estadísticos obtenidos en el modelo representado por la ecuación (2) y el segundo modelo ensayado, representado por la ecuación (5), se concluye que el modelo estimado:
lt obtenidos = 0,772141*kg molidos
representa apropiadamente los datos, y la Figura 3 muestra la concordancia entre los valores observados y predichos.
Puesto que el modelo encontrado representa adecuadamente los datos, se puede usar para efectuar predicciones de valores futuros, puntuales y por intervalos de confianza.
Validación del modelo adoptado
Con el objetivo de validar el modelo adoptado, se utilizó para predecir los litros de vino obtenidos en el año 2005 en función de los kilogramos de uva molidos.
Para 12.000.000 kg de uva molida, según el modelo lineal sin constante, se obtendrían 9.265.692 lt de vino. El intervalo de confianza a un 95% es (9.123.012, 9.408.372). Comparando el valor estimado con el valor real de 9.230.000 lt de vino, éste se encuentra contenido en él, lo que demuestra que el modelo al cual se arriba ajusta adecuadamente los datos.
En la Figura 4 se puede apreciar un gráfico de probabilidad normal para los residuos. Puesto que la mayoría de ellos están cercanos a la recta, se puede considerar que provienen de una población normal. Una estadística descriptiva para los residuos proporciona un promedio muestral próximo a 37036,0 y desviación estándar igual a 133809,0; los coeficientes de Sknewness y Kurtosis son 0,903952, -0,395964 respectivamente, y se encuentran en el intervalo (-2,2) (Box et ál., 2005).
Conclusiones
El modelo lineal logrado, aunque sencillo permite observar la dependencia de los litros obtenidos en un proceso de vinificación con respecto a los kilogramos de uva que ingresan a una bodega, realizando total abstracción del resto de las variables que en un proceso de esta envergadura se presentan. Es útil para representar los datos y es una alternativa válida para modelar matemáticamente este tipo de procesos, en los cuales todavía el arte de la elaboración del vino y el criterio del enólogo son primordiales a la hora de la obtención del producto. El modelo que en este trabajo se presenta está validado con rigurosidad y por lo tanto es muy apropiado para realizar predicciones de valores futuros, puntuales y por intervalos de confianza, siendo aplicable a bodegas de gran envergadura para la producción de vinos tintos finos, similar a la estudiada en este trabajo.
Nomenclatura
y: Litros de vino obtenidos
x: Kilogramos de uva molidos
β, β0,β1: Coeficientes de los distintos modelos lineales.
ε: Error
Ho, H1: Hipótesis
Bibliografía
Box, G., Stuart Hunter, W., Estadística para Investigadores. Introducción al diseño de experimentos y análisis de datos., Ed Reverté S.A., México, 2005. [ Links ]
Datz, C., Kullmann, C., Winery Design., The Neues Publishing Company, 2006. [ Links ]
Flanzy, C., Enología: Fundamentos Científicos y Tecnológicos., AMV Ediciones, 2003. [ Links ]
Jolibert, F., Consommations energetiques et filière vinicole., Bios, 5 (22), 1991, pp. 51-53. [ Links ]
Montgomery, D., Peck, E., Vining, G., Introducción al Análisis de Regresión Lineal., Ed. CECSA, México, 2004. [ Links ]
Oreglia, F., Enología Teórico-Práctica., Instituto Salesiano de Artes Gráficas, Buenos Aires, 1978. [ Links ]
Palacios, C., Udaquiola, S., Rodriguez, R., Modelo matemático para la predicción de las necesidades de frío durante la producción de vino.Vol. 38, 2009. [ Links ]
Pérez López, C., Métodos Estadísticos con Statgraphics para Windows., Ed. RA-MA, 1998. [ Links ]
Santamaría, P., López, R., Gutierrez, A., García-Escudero E. Influencia de la temperatura en la fermentación alcohólica., Zubía, No. 7, 1995, pp. 137-149. [ Links ]
Storm, D., Winery Utilities: Planning, Design and Operation., Ed. Kluwer Academia / Plenum Publisher, 2001. [ Links ]
Yair, M., Winery Technology & Operations: A Handbook for Small Wineries., Wine Appreciation Guild, 1996. [ Links ]
Ziraldo, D, Anatomy Of A Winery: The Art Of Wine At Inniskillin., Key Porter Books, 2002. [ Links ]














