Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.30 no.1 Bogotá Apr. 2010
Juan David Velásquez1 , Fernán Alonso Villa2 y Reinaldo C. Souza3
1 Ingeniero civil. M.Sc., en Ingeniería de Sistemas y Ph.D., en Ingeniería-Área Sistemas Energéticos, Universidad Nacional de Colombia, Medellín. Profesor asociado, Escuela de Sistemas, Facultad de Minas, Universidad Nacional de Colombia, Medellín. Director, Grupo de Computación Aplicada, Facultad de Minas, Universidad Nacional de Colombia. jdvelasq@unal.edu.co 2 Ingeniero de Sistemas en Informática. Estudiante de M.Sc., en Sistemas, Universidad Nacional de Colombia, Medellín. fernanvilla@gmail.com 3 Mestre em Sistemas de Engenharia Elétrica, Pontificia Universidade Católica do Rio de Janeiro, Brasil. Ph.D. in Statistics, University of Warwick, Reino Unido. Profesor titular de la Facultade de Engenheria Eletrica, Pontificia Universidade Catolica, Rio de Janeiro, Brasil.reinaldo@ele.puc-rio.br
RESUMEN
Las redes neuronales, y en particular los perceptrones multicapa (MLP), han sido reconocidos como una de las más poderosas técnicas para estimar series de tiempo; sin embargo, la técnica de redes cascada-correlación (CC) es un fuerte competidor para pronosticar series temporales pues incorpora mejoras a los problemas de identificabilidad estadística del modelo del MLP. En éste artículo se compara el rendimiento de las redes CC respecto de otras técnicas, entre ellas el MLP, ANN y Arima, usando vrias series de tiempo no lineales del mundo real, con el fin de determinar si las CC ofrecen buenos resultados en la práctica. Los resultados indican que las redes CC, en la mayoría de los casos, son superiores a los MLP, ANN y Arima, logrando errores menores en magnitud que los reportados en la literatura usando dichas técnicas, mientras que en relación a DAN2 se lograron errores cercanos e incluso mejores.
Palabras clave: cascada-correlación, redes neuronales, series de tiempo, predicción, entrenamiento, validación, perceptrón multicapa, DANN2, Arima.
ABSTRACT
Artificial neural networks, especially multilayer perceptrons, have been recognised as being a powerful technique for forecasting nonlinear time series; however, cascade-correlation architecture is a strong competitor in this task due to it incorporating several advantages related to the statistical identification of multilayer perceptrons. This paper compares the accuracy of a cascadecorrelation neural network to the linear approach, multilayer perceptrons and dynamic architecture for artificial neural networks (DAN2) to determine whether the cascade-correlation network was able to forecast the time series being studied with more accuracy. It was concluded that cascade-correlation was able to forecast time series with more accuracy than other approaches.
Keywords: cascade correlation, neural network, time series, forecasting, fit, validation, multilayer perceptron, DAN2, Arima.
Recibido: febrero 16 de 2009 Aceptado: marzo 15 de 2010
IntroducciónA través del tiempo se han desarrollado un gran número de téccas para la predicción y el modelado de series temporales, debido principalmente a la importancia de este problema en muchas áreas del conocimiento. Por ejemplo, dichos modelos son usados en el campo empresarial para pronosticar los cambios en la demanda de determinado producto, tomar decisiones sobre niveles de inventario, insumos, etcétera.
Ha sido comúnmente aceptado que muchas series temporales poseen comportamientos que no pueden ser modelados de la mejor forma usando un modelo lineal. Es así entonces como se han venido aplicando técnicas no lineales al modelado y la predicción de series de tiempo, entre ellas: Arima (autoregressive integrates moving average) (Box y Jenkins, 1976); ARCH (autoregressive heteroscedastic model) de Engle (1982); ANN (artificial neural networks), ampliamente discutidas por Hornik y Stinchcombe (1989) y DAN2, descrito por Ghiassi et al. (2005) y Saidane y Ghiassi (2005). De dichas técnicas, los modelos de redes neuronales, y en particular los perceptrones multicapa (MLP, por sus siglas en in-glés), han sido ampliamente usados en muchos casos prácticos, y se ha demostrado su utilidad y valor en la solución de este proble-ma. Velásquez y Montoya (2005) desarrollaron un modelo híbrido para la predicción del índice de precios al consumidor en Colom-bia, mientras que Velásquez y González (2005) modelaron la diná-mica del índice de tipo de cambio real colombiano. Su éxito se debe a que dichos modelos son aproximadores universales de funciones que están definidas en un dominio compacto (Hornik y Stinchcombe, 1989; Cybenko, 1989; Funahashi, 1989). No obs-tante, el proceso de especificación de un MLP es difícil debido a la gran cantidad de pasos metodológicos que requiere, a los criterios subjetivos en cuanto a cómo abordar cada paso, y a que los resul-tados obtenidos en cada etapa son críticos.
Uno de los aspectos que dificultan el proceso de especificación es la falta de identificabilidad estadística del modelo. Las diversas consideraciones sobre este tema son el punto inicial para plantear modificaciones sobre la especificación del perceptrón multicapa, de modo que se obtengan nuevas configuraciones que puedan modelar y pronosticar series no lineales de una forma más simple y permitan obtener mejores resultados en comparación con otros modelos.
Desde este punto de vista, la red neuronal artificial conocida como cascada-correlación (CC) propuesta por Fahlman y Lebiere (1990) presenta ventajas conceptuales muy interesantes con relación al problema de identificabilidad de los MLP. Además, modificando un MLP es posible obtener una red CC.
Aunque una red CC podría realizar la regresión de funciones no lneales con una precisión superior a un MLP tradicional, en la literatura más relevante no se han reportado comparaciones entre los MLP y las redes CC cuando se modelan o pronostican series temporales no lineales, y consecuentemente, esta hipótesis no ha sido demostrada en la práctica. Así, un objetivo de este artículo es el de establecer una base para la comparación de MLP y redes CC. En este orden de ideas, en la literatura tampoco se ha comparado el rendimiento de las CC con respecto a técnicas como DAN2 y ANN al pronosticar series de tiempo. Asimismo, otro objetivo es el de establecer si las redes CC tienen un rendimiento apropiado para el pronóstico de series.
En este artículo se presentan las redes CC como un modelo factible para el pronóstico de series temporales y posiblemente superior a los MLP. Además, se realiza el análisis de tres casos reales para determinar si realmente existen ganancias derivadas del uso de redes CC en comparación con MLP, y resultados obtenidos por otros autores al estimar series de tiempo con otros modelos de redes neuronales, tales como DAN2, dado que en la literatura más relevante no se encuentra una comparación empírica de dichas técnicas contra CC que permita establecer si es beneficioso pronosticar series de tiempo con redes CC.
A continuación se presenta el modelo del MLP y las dificultades de su proceso de especificación. Igualmente, las redes CC y las ventajas conceptuales que posee sobre los MLP. Seguidamente, se describen los casos de análisis utilizados y se analizan los resultados obtenidos. Finalmente, se concluye.
El modelo
Un perceptrón multicapa (MLP, por sus siglas en inglés) es un tipo de red neuronal que imita la estructura masivamente paralela de las neuronas del cerebro. Desde un punto de vista matemático, es un modelo que puede aproximar cualquier función continua definida en un dominio compacto con una precisión arbitraria previamente establecida (Hornik y Stinchcombe, 1989; Cybenko, 1989; Funahashi, 1989). En la práctica, los MLP se han caracterizado por ser muy tolerantes a información incompleta, inexacta o contaminada con ruido (Masters, 1993), por lo que han sido usados en la modelación empírica de series temporales no lineales; Zhang et ál. (1998) presentan una revisión general sobre el estado actual, mientras que aplicaciones específicas son presentadas por Heravi et ál. (2004) y Kuan y Liu (2000), entre muchos otros.
Una serie temporal se define como una secuencia de observaciones en el tiempo y1, y2, …, yT, para la cual se pretende construir una función que permita obtener yt en función de sus valores pasados, yt-1, yt-2,…,yt-p. Dicha función puede ser especificada como un MLP que puede ser representado matemáticamente como.
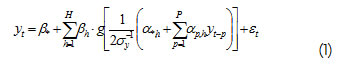
donde los parámetros Ω = [β*, βh, α*,h, αp,h], h = 1…H, p = 1…P son estimados usando el principio de máxima verosimilitud de los residuales, que equivale a la minimización de una función de costo definida usualmente como el error cuadrático medio. La ecuación (1) equivale a un modelo estadístico no paramétrico de regresión no lineal (Sarle, 1994). En (1) se asume que εt sigue una distribución normal con media cero y varianza desconocida σ2. H representa el número de neuronas en la capa oculta. P es el número de rezagos de la variable dependiente. Y g(·) es la función de activación de las neuronas de la capa oculta. En el contexto de las series temporales el modelo puede ser entendido como una combinación lineal ponderada de la transformación no lineal de varios modelos autorregresivos. En la Figura 1se exhibe una representación pictórica del modelo postulado en (1).
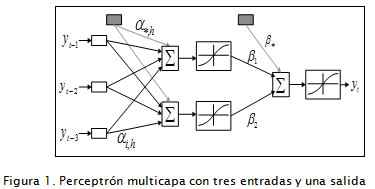
La especificación del MLP
El proceso de especificación de un MLP es difícil debido a la gran cantidad de pasos metodológicos que requiere ( la selección de las entradas, la determinación de las neuronas de la capa oculta, la estimación de los parámetros (Ortiz et ál., 2007), etc.) , a los criterios subjetivos en cuanto a cómo abordar cada paso, y a que los resultados obtenidos en cada paso son críticos.
Uno de los aspectos que dificultan el proceso de especificación es la falta de identificabilidad estadística del modelo. Esto se refiere a que los parámetros óptimos no son únicos para una configuración específica de un modelo (número de entradas, cantidad de neuronas en la capa oculta, funciones de activación, etc.), y un conjunto de datos dado, debiéndose a que:
-Se pueden obtener múltiples configuraciones idénticas en comportamiento cuando se permutan las neuronas de la capa oculta, manteniendo vinculadas las conexiones que llegan a dichas neuronas.
-Cuando las neuronas de la capa oculta tienen funciones de activación simétricas alrededor del origen, la contribución neta de la neurona a la salida de la red neuronal se mantiene igual si se cambian los signos de los pesos que entran y salen ella.
-Si los pesos de las conexiones entrantes a una neurona oculta equivalen a cero, es imposible determinar el valor del peso de la conexión de esa neurona oculta a la neurona de salida.
-Si el peso de la conexión de una neurona oculta hacia la neurona de salida es cero, es imposible identificar los valores de los pesos de las conexiones entrantes a la neurona oculta.
Las consideraciones anteriores sobre la identificabilidad del modelo son el punto inicial para plantear modificaciones sobre la especificación del MLP de manera tal que se obtengan nuevas configuraciones que puedan modelar y pronosticar series no lineales de una forma más simple y permitan obtener mejores resultados en comparación con otros modelos.
Las redes cascada correlación
La red neuronal artificial conocida como cascada-correlación (CC) propuesta por Fahlman y Lebiere (1990) está diseñada siguiendo el esquema de crecimiento de red;se comienza con una red mínima sin capas ocultas, es decir, con sólo algunas entradas y uno o más nodos de salida. Las neuronas ocultas son agregadas una a una en la red, obteniendo de esta forma una estructura multicapa. En la Figura 2 se presenta el esquema de una red CC. En el proceso de adición de neuronas ocultas a la red, cada nueva neurona recibe una conexión sináptica de cada una de las neuronas de entrada y también de las neuronas ocultas que la preceden. Luego de agregar la nueva neurona oculta, los pesos sinápticos de su entrada son congelados, mientras que los pesos de su salida son entrenados repetidamente. Este proceso es continuo hasta que se alcanza un rendimiento satisfactorio.
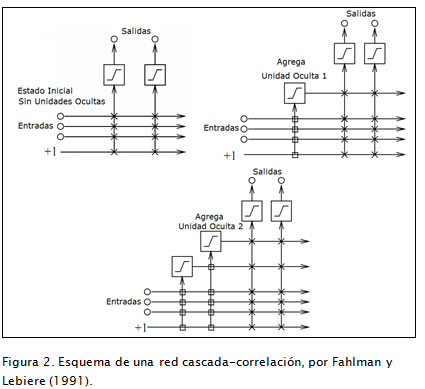
Las redes CC presentan ventajas conceptuales muy interesantes con relación al problema de identificabilidad de la especificación del MLP. A partir de un MLP puede obtenerse una red CC realizando las siguientes modificaciones:
-Se restringe a que la función de activación de las neuronas de la capa de salida sea lineal.
-Se agregan conexiones desde las neuronas de entrada hasta la neurona de salida. Esto equivale a introducir dentro del modelo una componente que es la combinación lineal de las entradas. Tal modificación facilita que el modelo pueda capturar la componente lineal del conjunto de datos estudiado.
-Desde la j-ésima neurona de la capa oculta se agregan conexiones de salida que entran a las neuronas j+1, j+2, … Esto tiene el efecto de evitar que las neuronas de la capa oculta puedan permutarse, por lo que se reduce la multiplicidad de modelos con desempeño similar.
Así, de una red CC puede obtenerse un MLP imponiendo algunas restricciones a los pesos de las conexiones.
Consecuentemente con lo anterior, una red CC podría realizar la regresión de funciones no lineales con una precisión superior a un MLP tradicional. Eso (el problema general de regresión) ya ha sido abordado en la literatura; pero el problema del modelado y la predicción de series temporales es más complejo que el de regresión, pues se debe tener en cuenta el orden de los datos así como las nuevas propiedades estadísticas que este ordenamiento induce sobre la información.
Casos de aplicación
En esta sección se presenta la comparación entre las redes CC y los modelos MLP y DAN2 para distintas series de tiempo reales y para varias configuraciones de los modelos de redes neuronales. Las series utilizadas son "Pasajeros de una aerolínea", de Box y Jenkins, "Usuarios de un servidor de Internet" y "Equipos contra la contaminación", ampliamente estudiadas en la literatura por diversos autores. Para la comparación, según sea el caso, se toma el MSE o SSE al pronosticar cada serie con diferentes modelos de redes CC; los mejores resultados obtenidos por Ortiz et ál. (2007) al pronosticarlas con MLP; los registrados por Ghiassi et ál. (2005) al pronosticarlas con modelos DAN2; y los reportados por otros autores. Así, se compara el desempeño de CC contra el del MLP y DAN2 a través del SSE o MSE, y con fines ilustrativos se presentan algunos resultados obtenidos en otras investigaciones. Las tres series mencionadas fueron elegidas debido al comportamiento no lineal que poseen, como se puede apreciar en las figuras 3, 4, 5.
Primer caso: Pasajeros de una aerolínea
Esta serie de tiempo contiene el registro del número total de pasajeros transportados al mes por una aerolínea, desde enero de 1949 hasta diciembre de 1960. Cada uno de los trece modelos, contenidos en la Tabla 1 fue estudiado por Faraway y Chatfield (1998) utilizando un modelo de redes neuronales (ANN), por Ghiassi et ál. (2005) mediante DAN2 y por Ortiz et ál. (2007) con un MLP. Para cada modelo los datos de la serie se transformaron utilizando la función logaritmo natural; se usaron los primeros 120 datos para entrenamiento y los 12 últimos para validación, tal como fue realizado por Faraway y Chatfield (1998). En la Figura 3 se muestran los valores reales y los pronosticados empleando el modelo 1 de CC de la Tabla 1 .
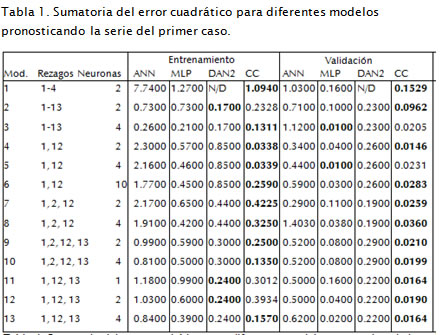
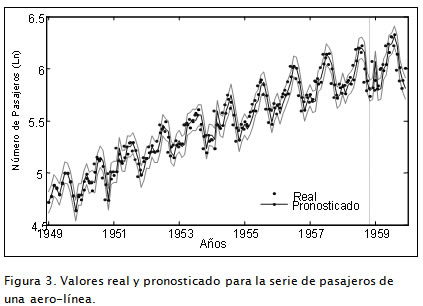
Faraway y Chatfield (1998), Ghiassi et ál. (2005) y Ortiz et ál. (2007) reportaron de cada uno de los modelos de la Tabla 1 la sumatoria del error medio cuadrático (SSE) para las muestras de entrenamiento y validación, al pronosticarlos con DAN2 y MLP, respectivamente. Se pronóstico la serie con los modelos respectivos de CC y se estimó el estadístico de ajuste para las muestras en entrenamiento y de validación.
En la Tabla 1 se resumen los resultados obtenidos; nótese que los errores logrados con CC para los modelos 1, 4, 6, 7, 9, 10 y 13, tanto en entrenamiento como en validación, son mejores que los reportados con ANN, MLP y DAN2.
Para los modelos 2, 11 y 12 (Tabla 1 ), en entrenamiento, los errores obtenidos con CC son 26,98%, 20,32% y 38,99% mayores que los reportados con DAN2, respectivamente. Sin embargo, estos errores son tolerables dado que están relativamente cercanos a los reportados con DAN2 y son menores que los proporcionados por ANN y MLP. Además, los errores alcanzados en validación resultan menores que los reportados con ANN, MLP y DAN2 para los tres modelos en cuestión.
De la Tabla 1 , los errores logrados con CC en entrenamiento para los modelos 3, 5 y 8 son menores que los reportados con ANN, MLP y DAN2, mientras que en validación los errores obtenidos con CC para los modelos 3, 5 y 8 son 51,22%, 56,71%, y 16,67% más altos que los logrados con MLP, respectivamente. No obstante, se puede considerar que estos errores de validación son tolerables, al ser menores que los hallados con DAN2 y ANN.
En la Tabla 2 se presentan 4 modelos estudiados por Ghiassi et ál., (2005) mediante DAN2; en los modelos 2 y 3 las redes CC fueron superiores a DAN2, tanto en entrenamiento como en validación. Sin embargo, en el modelo 1 y 4 DAN2 fue superior en entrenamiento y CC en validación.
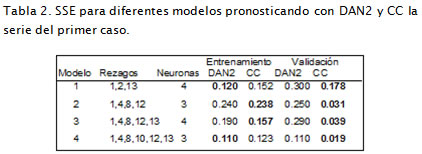
Claramente, para esta serie en particular, 7 de los 13 modelos de CC de la Tabla 1 fueron superiores que los modelos de ANN, MLP y DAN2; además, al pronosticar los 13 modelos todos los errores fueron cercanos a los reportados en la literatura. Entonces, los modelos de CC son una opción viable para pronosticar esta serie.
Segundo caso: Usuarios de un servidor de Internet
Esta serie temporal registra el número de usuarios que iniciaron sesión en un servidor de Internet durante 100 minutos, para un total de 100 observaciones. Fue estudiada por Makridakis et ál. (1998) mediante modelos Arima, Ghiassi et ál. (2005) con DAN2. Además, en Makridakis et ál. (1998) se afirma que esta serie refleja la no estacionalidad del proceso que representa. En los experimentos, de los 100 datos se tomaron los primeros 80 para entrenamiento, y los restantes para validación, tal como lo hicieron Ghiassi et ál. (2005). En la Figura 4 se presentan los valores reales y los pronosticados de la serie de tiempo con el modelo CC-1 de la Tabla 3 .
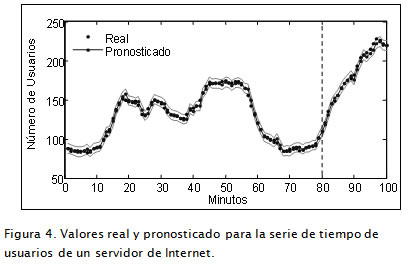
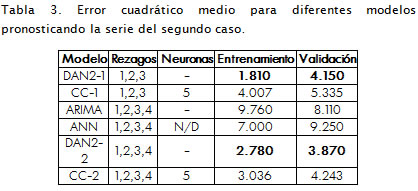
Se experimentó con varios modelos pronosticando la serie de este caso hasta obtener un error menor que el reportado en Ghiassi et ál. (2005) para ANN y Arima y que también fuera cercano a los obtenidos con DAN2, en la Tabla 3 se resumen los errores logrados y reportados, tanto en entrenamiento como en validación. Los rsultados indican que los errores hallados con los dos modelos de CC (CC-1 y CC-2) son menores que los reportados con ANN y Arima. Comparando los modelos similares de CC y DAN2, para el error de entrenamiento del modelo CC-1 es 54,83% más alto que el reportado para DAN2-1, mientras que para validación es 22,21% más alto. Asimismo, el error de entrenamiento del modelo CC-2 es 8,43% más alto, y en validación lo es 8,79%; los errores logrados tanto con CC-1 como en CC-2 son relativamente cercanos a los reportados con modelos similares de DAN2. Claramente, estos errores son aceptables, y los modelos mencionados de CC son adecuados para pronosticar en particular la serie de este caso.
Tercer caso: Equipos contra la contaminación
En la serie de este caso se encuentra almacenado el envío mensual de equipos contra contaminación desde enero de 1986 hasta otubre de 1996, para un total de 130 datos. La serie fue estudiada por Makridakis et ál. (1998) mediante modelos Arima, y por Ghiassi et ál. (2005) a través de DAN2. Además, los datos muestran una tendencia a fluctuar con el tiempo en una magnitud variable, demostrando una no estacionalidad en la varianza (Makridakis et ál., 1998); esto se puede apreciar en la Figura 5, donde se despliegan los valores reales y pronosticados usando el modelo CC2 de la Tabla 4 . En los experimentos se transformó la serie utilizando la función logaritmo natural (base - e); se usaron los primeros 106 datos para entrenamiento y los 24 últimos (dos años) para validación, tal como fue realizado por Makridakis et ál. (1998).
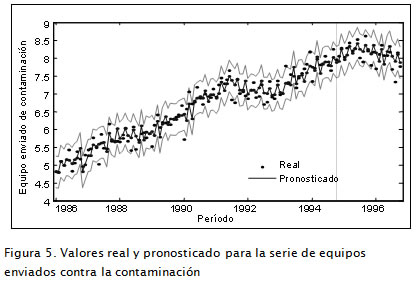
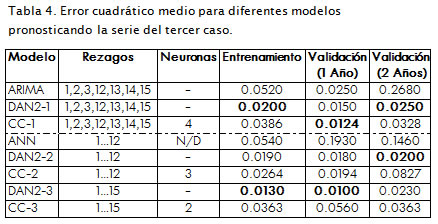
Similar al segundo caso, se experimentó con varios modelos pronosticando la serie de este caso hasta obtener un error menor que el reportado en Ghiassi et ál. (2005) para ANN y Arima y que también fuera cercano a los reportados con DAN2, en la Tabla 4 se resumen los errores alcanzados y reportados tanto para entrenamiento como para la validación de 12 y 24 meses, es decir, 1 y 2 años, respectivamente. Los resultados indican que los errores logrados con los dos modelos de CC son menores que los reportados con ANN y Arima. Comparando los modelos similares de CC y DAN2, el error de entrenamiento del modelo CC-1 es 48,19% más alto que el reportado para DAN2-1, mientras que para validación del primer año es 20,97% menor, y para la validación del segundo año es 23,78% mayor. Además, el error de entrenamiento del modelo CC-2 es 23,78% más alto, en validación de un año lo es 7,22% y de dos años 75,82%. Finalmente, los errores con CC-3 en entrenamiento, validación (1 año) y validación (2 años) son 64,19%, 82,14% y 36,64% mayores, respectivamente.
Los errores con CC-1, CC-2 y CC-3 son menores que los reportados con ANN y Arima, además, están relativamente cercanos a los reportados con modelos similares de DAN2. Claramente, estos errores son tolerables, y los modelos mencionados de CC resultan ser una opción razonable para pronosticar en particular la serie de este caso.
Conclusiones
En este trabajo se muestra que las redes neuronales, y en particular los MLP, han sido reconocidos como una de las técnicas más adecuadas para modelar y pronosticar series de tiempo; sin embargo, su proceso de especificación es difícil debido a la falta de identificabilidad estadística del modelo. Es así como el tipo de redes CC se presenta como una solución atractiva, toda vez que incorpora varias soluciones a dichos problemas.
Además, se ha probado experimentalmente pronosticando tres series de tiempo del mundo real, que las redes cascadacorrelación son una técnica apropiada para el pronóstico de series temporales. Dado que en la mayoría de modelos usados para los experimentos las CC mostraron ser superiores a los MLP, ANN y Arima, revelando errores menores en magnitud que los reportados en la literatura con estas técnicas, es decir, CC alcanzó un mejor rendimiento que el reportado con MLP, ANN y Arima. Además, varias veces se lograron errores cercanos, e incluso menores, que los reportados con DAN2. Consecuentemente, las redes CC son una arquitectura alternativa para modelar y predecir series temporales.
Esta investigación tiene un impacto asociado al desarrollo de nuevos conocimientos en el área de la predicción, que se ve impactada por la incorporación de la red cascada-correlación al conjunto de técnicas usadas para el modelado y la predicción de series de tiempo, así como por la aplicabilidad práctica que tiene. Ello es debido a que hay un valor agregado relacionado con la utilidad del modelo para representar la dinámica de series financieras y económicas.
Agradecimientos
Este artículo se realizó en el marco del proyecto de investigación "Modelado y predicción de series temporales no lineales usando redes cascada-correlación", financiado por la DIME y la Universidad Nacional de Colombia (Medellín).
Bibliografía
Box, G., Jenkins, G., Time series analysis, forecasting and control., San Francisco, Holden-Day., 1976. [ Links ]
Campbell, M. J., Walker, A. M., A survey of statistical work on the mackenzie river series of annual canadian lynx trappings for the years 1821-1934 and a new analysis., Journal of the Royal Statistical Society. Series A. Statistics in Society., Vol. 140, NO. 4, 1977, pp. 411-431. [ Links ]
Cybenko, G., Approximation by superpositions of a sigmoidal function., Mathematics of Control: Signals and Systems. Vol. 2, 1989, pp. 202-314 [ Links ]
Darbellay, G., Slama , M., Forecasting the short-term demand for electricity: do neural networks stand a better chance?., International Journal of Forecasting. Vol. 16, 2000, pp. 71-83. [ Links ]
Engle, R., Autoregressive conditional heteroscedasticity with estimates of the variance of UK inflation., Econometrica. Vol. 50, NO. 4, Jul., 1982, pp. 987-1008. [ Links ]
Fahlman, S. E., Lebiere, C., The Cascade-Correlation learning architecture. Advances in Neural Information Processing Systems. Advances in Neural Information Processing Systems. Vol. 2, 1990, pp. 524-532. [ Links ]
Faraway, J., Chatfield, C., Time series forecasting with neural networks: A comparative study using the airline data. Applied Statistic. Vol. 47, NO. 2, 1998, pp. 231-250. [ Links ]
Funahashi, K., On the approximate realization of continuous mappings by neural networks. Neural Neworks. Vol. 2, 1989, pp. 183-192. [ Links ]
Ghiassi, M., Saidane, H., Zimbra, D., A dynamic artificial neural network model for forecasting time series events., International Journal of Forecasting. Vol. 21, NO. 2, 2005, pp. 341-362. [ Links ]
Heravi, S., Osborn D., Birchenhall, C., Linear versus neural network forecasts for european industrial production series., International Journal of Forecasting. Vol. 20, 2004, pp. 435-446. [ Links ]
Hornik, K., Stinchcombe, M., White, H., Multilayer feedforward networks are universal approximators., Neural Networks. Vol. 2, NO. 5, 1989, pp. 359-366. [ Links ]
Kuan, C., Liu, T,. Forecasting exchange rates using feedforwad and recurrent neural networks. Journal of Applied Econometrics. Vol. 10, 1995, pp. 347-364. [ Links ]
Makridakis, S. G., Wheelwright, S. C., Hyndman, R. J., Forecasting: Methods and applications., New York John Wiley & Sons., 1998. [ Links ]
Masters, T., Practical neural network recipes in C++. New York, Academic Press, 1993. [ Links ]
Ortiz, D. M., Villa, F. A., Velásquez, J. D., Una Comparación entre Estrategias Evolutivas y RPROP para la Estimación de Redes Neuronales., Avances en Sistemas e Informática. Vol. 4, NO. 2, 2007, pp. 135-144. [ Links ]
Rao, T. S., Gabr, M., An introduction to bispectral analysis and bilinear time series models. Lecture Notes in Statistics. Vol. 24, 1984, pp. 528-535. [ Links ]
Saidane, H., Ghiassi, M., A dynamic architecture for artificial neural networks. Neurocomputing. Vol. 63, Ene., 2005, pp. 397-413. [ Links ]
Sarle, W., Neural networks and statistical models., The 19th Annual SAS Users Group Int. Conference. Cary, NC: SAS Institute, 1994, pp. 1538-1550. [ Links ]
Velásquez, J. D., González, L. M., Modelado del índice de tipo de cambio real colombiano usando redes neuronales artificiales., Cuadernos de Administración. Vol. 19, NO. 32, 2005, pp. 319-336. [ Links ]
Velásquez, J. D., Montoya, S. F. Modelado del índice de precios al consumidor usando un modelo híbrido basado en redes neuronales artificiales. Revista Dyna. Vol. 72, NO. 147, 2005, pp. 85-93. [ Links ]
Zhang, G., Patuwo, B., Hu, M., Forecasting with artificial neural networks: the state of the art., International Journal of Forecasting. Vol. 14, Nro. 1, 1998, pp. 35-62. [ Links ]
Zhang, G., Time Series forecasting using a hybrid ARIMA and neural network model., Neurocomputing., Vol. 50, 2003, pp. 159-175. [ Links ]














