Numerical modeling of the fracture process in reinforced concrete by means of the continuum strong discontinuity approach. Part I: formulation

¹ Civil Engineer. M.Sc., in Struture. Ph.d., in Structural Analysis, Universidad Politécnica de Cataluña, Spain. Professor, Faculty of Engineering, Universidad Nacional de Colombia, Bogotá. dllineros@unal.edu.co ² Civil Engineer. Ph.D., in Civil Engineering, Universidad Politécnica de Cataluña, Spain. Professor, Department of Strength of Materials and Structures, Universidad Politécnica de Cataluña. Spain. oliver@cimne.upc.edu ³ Mechanic and Electrical Engineer. M.Sc., in Science of Enginnering. Ph.D., in Science of Enginnering, Universidad Federal de Rio de Janeiro, Brasil. Researcher, CIMEC/Intec – CONICET, Santa Fe, Argentina. ahuespe@intec. unl.edu.ar

ABSTRACT

Reinforced concrete structures generally refers to beams, columns and walls which are constituted by complex lattices of steel bars embedded in a concrete matrix, exhibiting multiple cracks due to high external loads. This paper presents the formulation of a numerical model aimed at describing the fracture process in reinforced concrete, from the volumetric ratio of concrete and steel Crack formation and propagation in a composite material is described in the model by an enhanced strain field, such as that established in the continuum strong discontinuity approach and mixture theory. The composite material is constituted by a concrete matrix and one or two steel bar orthogonal packages. The steel and concrete are represented by a one-dimensional plasticity model and a scalar damage model having different tension and compression strength, respectively. The dowel action and the bond-slip effects between the bars and the matrix are described with additional models relating component material stress and strain. It is concluded that the proposed model can easily be implemented in the finite element method, due to several conventional nonlinear numerical process characteristics which remain. The model would also allow the problem to be analysed at macroscopic scale, thereby avoiding a finite element mesh having to be constructed for each component material and its interaction effects and reducing computational costs.

Keywords: computational mechanics, fracture mechanics, strong discontinuity, mixture theory, reinforced concrete.

Received: febreary 19th 2009

Accepted: jun 11th 2010

Introduction

The reinforced concrete fracture process can be predicted by means of a numerical model able to capture crack formation and propagation of all solid points. Implementing the model in the finite element method allows any structural member's geometry and loading regime to be represented.

Reinforced concrete structure numerical modeling can be done on different scales. The finite elements mesh represents each material separately on a mesoscopic scale, including special elements describing the interaction between concrete and steel. This kind of analysis usually requires fine mesh and consequently high computational costs. On the other hand, each material point inside a finite element on a macroscopic scale has a constitutive model of composite material representing the behavior of a set of steel bars embedded in a concrete matrix.

A lot of models have satisfactorily described the behavior of reinforced concrete (Feenstra and de Borst, 1995; Pietruszczak and Xu, 1995; Belletti, Cerioni et al., 2001; Jendele, Cervenka et al., 2001; Luccioni and Lopez, 2002; Belletti, Bernardi et al., 2003; Pietruszczak and Winnicki, 2003; Luccioni, Lopez et al., 2005; Yu and Ruiz, 2005; Ruiz, Carmona et al., 2006; Menin, Trautwein et al., 2009; Shi, 2009), with the followings restrictions. They do not use an algorithm for describing crack paths independently of the direction of the finite elements mesh. They lose the context of continuum mechanics when the fracture process begins, consequently requiring additional ad hoc relationships for defining the mechanical behavior between the faces of a crack. Unlike material bifurcation analysis, the criteria used for establishing the formation of a crack are explicitly independent of the condition regarding displacement jump. In some cases, a distributed cracking state is considered from the concrete's inelastic regime in which cracks maintain a constant spacing evaluated in an analytical form. Consequently, the formation of a macro-crack located in composite material cannot be captured. Other models require explicit relationships between traction and jump in the concrete matrix and the steel bars.

The formulation presented in this work was expected to overcome the previous restrictions by means of a homogenous macroscopic model of reinforced concrete, based on the mixture theory ruesdell and Toupin, 1960; Oller, 2003) which describes the formation of cracks in the context of continuum mechanics and applying the continuum strong discontinuity approach (CSDA) (Oliver, 1996a; Oliver, 2000; Oliver and Huespe, 2004a; Oliver, Huespe et al., 2006; Linero, Oliver et al., 2007; Oliver, Linero et al., 2008).

Constitutive models of the component materials

Concrete matrix behaviour can be described with an isotropic scalar damage model (Lemaitre, 1992; Lemaitre and Desmorat, 2005) in which its tensile strengths^c_t is different to its compression strength s^c_c as indicated Figure 1a..

The constitutive model's damage criteria particularly compares the evolution variable with a special strain field norm which has been modified by a factor associated with the sign of effective principal stress (Oliver, Cervera et al., 1990). The tangent constitutive equation for a model representing simple concrete is expressed thus:

where e^•c and s^•c; are the strain rate tensor and the stress rate tensor, respectively. The tangent constitutive tensor C^c_tg is a function of strain state e^c and of the loading history indicated by the internal variables of the damage model a^c.

The axial behaviour of the steel bars embedded in the concrete matrix is represented by the slipping bar model which combines a plasticity isotropic one-dimensional model with softening strain (Simó and Hughes, 1998; de Souza, Peric et al., 2008) and adherence between the steel bar rib and the surrounding concrete. The material mechanics properties are Young's modulus Ea , the yielding stress to tension or compression y s_y; and the hardening modulus H^a . Steel stress defined as adhs_adh is obtained from pull-out tests when adherence with the concrete has disappeared (Gambarova, Rosati et al., 1989; Hutchinson and Jensen, 1990; Naaman, Namur et al., 1991).

If there is perfect adherence then the slipping bar model coincides with the softening plasticity model and its inelastic stage begins after reahing the steel yielding stress, that is y adh s_y< s_adh , as shown in Figure 1b. On the other hand, if adherence disappears before reaching the yielding stress, that is y adhs_y> s_adh , then the slipping bar model indicates that the elastic regime is limited by stress adh s_adh , followed by perfect plastic stage associated with the slipping of the bars in the matrix (Figure 1c).

The tangent constitutive equation of the slipping bar model relates to normal stress rate σ& a and normal strain rate ε&a in the direction of the bar as:

where the tangent elasticity modulus E^a_tg depends on the plastic strain e^a_p , the internal variables of plasticity model a^a a and the relationship between limit stress y s_yy s_adh .

After that, a slight crack is formed, shear force being mainly supported steel reinforcement's ability to direct shear to the sides of the crack (Park and Paulay, 1975; Nawy, 2008). This phenomenon is named dowel action and it is represented by a softening scalar plasticity model which relates shear stress rate t^•a to engineering shear strain rate g^•a at the cross-section of the bars, as indicated in the tangent constitutive equation:

It can be observed in Figure 1d that tangent shear modulus a G^a_tg is equal to steel shear elasticity modulus G^a after reaching yielding shear stress y t_y . The inelastic regime determines the steel's next stage.

Constitutive model of reinforced concrete as a composite material

Each point on a solid has two sets of steel bars embedded in a concrete matrix; they are orientated in directions r and s respecttively, as shown in Figure 2. The mixture theory establishes that each infinitesimal volume of composite mial results from adding the substances forming it (Truesdell and Toupin, 1960; Oller, 2003). In a parallel system, each component's contribution to composite stress is a function of their volumetric participation and the strain of each component is the same. However, the strain in a specific orientation is evaluated when the one-dimensional behavior of the bars has been defined.

The compatibility between the composite material strain tensor and the strain of each component material were defined here by the following hypothesis. The strain tensor of matrixe^c was equal to the strain tensor of composite material e . The normal strain e^ar obtained from axial behavior of the bars in r direction was equal to the normal term of composite material strain tensor e_rr . The normal strain e^as obtained from the axial behavior of the bars in s direction was equal to normal term e_ss in s direction of the composite material strain tensor. Given that the bars crossing a crack had shear capacity, it was assumed that the engineering shear strain g^a of the bars was equal to term g_rs in the rs plane of the composite material strain tensor.

The following equations were derived from the previous compatibility conditions:

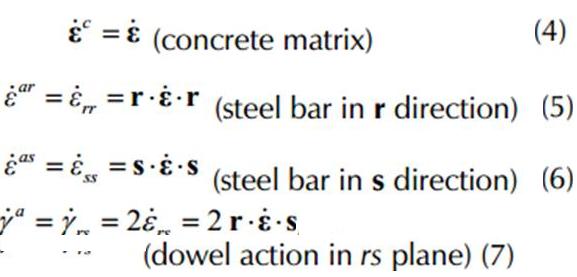
Given that the composite material strain rate tensor e^• is wellknown, the strain rate of each component material and of the interaction effects were computed with equations (4) to (7). These strain rates were put into the respective constitutive model to obtain the stress of each material and its interaction effects.

The stress rate tensor of concrete matrix s^•c was obtained by means of the isotropic damage model. On the other hand, the normal stress rate of the steel bars s^•ar and s^•as as oriented in r and s directions were obtained by applying the slipping bar model. The effect of the dowel action was observed in the shear stress rate of the steel bars t^•a obtained from the previously indicated model.

Each component's contribution to the composite material's behaviour was defined by the volumetric participation factor which corresponded to the volume ratio of the component material regarding the composite material's whole volume. The volumetric participation factor of the concrete matrix was named k^c, whereas k^arand k^aswere the volumetric participation factor of the steel bars orientated in r and s directions, respectively. If the composite material volume was the sum of its components, then it had fulfilled the condition that k^c+k^ar+k^as=1.

The stress rate tensor of composite material corresponded to the sum of the stress tensors of the concrete matrix and steel bars multiplied by its respective volumetric participation factor, thus:

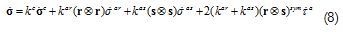
The tangent constitutive equation of composite material was obtained by substituting the compatibility equations of the strain rates of each component material in its respective tangent constitutive equation and replacing the result in the previous equation, thus:

where tangent constitutive tensor C_tgwas equal to:

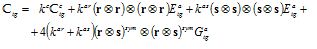(10)

The previous process defined the constitutive model of reinforced concrete as being a parallel system where each constitutive material had its own model Figure 3.

Kinematic description of composite materials by means of the CSDA in the continuum

Constructing a reinforced concrete constitutive model entails modelling composite materials using kinematics so that displacement rate vectors and consequently the strain rate tensor become fields associated with the composite material. A kinematic description due to continuum strong discontinuity approach (CSDA) (Oliver, 1996b; Oliver and Huespe, 2004b; Oliver and Huespe, 2004a; Oliver, Huespe et al., 2006) can thus be applied to predicting the formation and propagation of cracks in a solid.

This approach establishes the existence of a jump in the displacement field [[u]] on the failure surface which is able to generate unbounded values (in a distributional sense) in the strain field.

Let W be a solid exhibiting strong discontinuity on S of normal n which splits the body into domains W⁺and W^- , as shown in Figura 2a The displacement rate at material point x and time t was defined as:

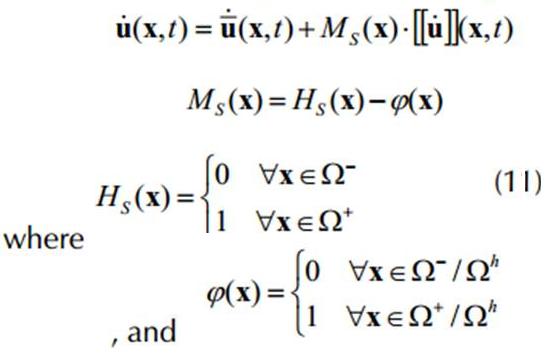
Furthermore, u^• and [|u^•|] corresponded to the continuous part and displacement rate jump in the discontinuity, respectively.

In the continuum, the unit jump function M_s(x) was computed as being the subtraction between Heviside’s function H_s(x) and an arbitrary continuous function φ(x). limited by a small band Ω^h in S , as indicated in Figure 4

The strain rate field was evaluated with the symmetrical differential operator on the displacement rate field, so that the strain was split into a compatible part in terms of continuous displacement and an enhanced part in terms of displacement jump.

Given that the gradient of Heaviside's function produced an unounded value equal to DH_s = d_sn , the strain rate could be indicated as the sum of a regular or bounded part, thus:

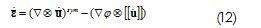
plus a singular or unbounded part equal to (d_sn X [|u^•|]) . Dirac's delta function S d_s was approximately equal to a regularised function d^h_s applied in a band Ω^h with width h≈0 which was inside discontinuity S . This regularised function was:

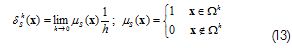
where μ_s was a collocation function on Ω^h therefore, the strain rate of composite material was equal to:

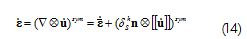
Band width h took a small value different to zero, before forming a strong discontinuity. This previous stage is named weak discontinuity and showed a bounded strain rate value, thus:

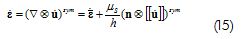
Bifurcation analysis in the material

In the tests where reinforcement was uniformly distributed throughout the whole member (after the elastic regime of the concrete), two stages were distinguished. Initially a lengthy distributed cracking stage showed many slight cracks having constant separation due to the steel's capacity and to good adherence between the concrete and the bars. In a second step, called discontinuous or located failure stage, it was observed that the opening of a few cracks prevailed on the others, whereas structural capacity decayed. In the context of continuum mechanics, the bifurcation analysis of the material led to determining the beginning and the direction of the cracks in the located failure stage.

The displacement rate field, the strain rate and the stress rate were defined on the composite material scale at a material point. This led to assuming that the discontinuous bifurcation analysis used in homogenous materials (Rice, 1976; Runesson et al., 1991) could be applicable to composite materials such as the rein-forced concrete presented in this work (Linero et al., 2009).

Considering that the tangent constitutive tensor of the composite material in domains W⁺y W^-, were the same, and replacing the constitutive equation of the composite material in the traction continuity condition, then:

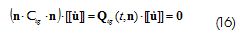
According to the aforementioned kinematics, a jump in the displacement rate field different from zero |u^•|]≠0 was a sufficient condition for the existence of a strong discontinuity mode. Therefore, fulfilling the previous equation, the localisation tensor Q_tg(t,n) must have been null at bifurcation time t=t_B and in the direction normal to discontinuity n=n_B, so that:

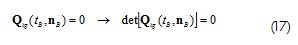
Conclusions

Formulating a constitutive model directly describing the strain and stress fields in a point of composite material such as reinforced concrete offers two important advantages.

It facilitates implementation in the finite elements method since many of the ingredients of the conventional numerical procedure are kept. Likewise, it allows the problem to be analysed on a structural or macroscopic scale thereby avoiding high computational costs because of the mesh for each component material and its effects of interaction.

The continuum strong discontinuity approach can be easily applied to materials reinforced with long bars, considering a common strain field such as that established by the mixture theory. The formulation presented here preserves the context of continuous mechanics, although each material point has a discontinuous nature due to the development of cracks and the mechanical difference between concrete and steel.

The slipping fibre model includes the mechanical behaviour of the bar and the difference between the strain of the concrete matrix and steel bars caused by slipping between both materials. This model maintains the strain compatibility of the component materials as a basic hypothesis of the mixture theory.

The dowel action is defined as being the shear capacity of the reinforcement bars crossing a crack. A one-dimensional law of steel shear behaviour is introduced into the formulation which is characterised by the material's mechanical properties and the geometric properties pertaining to the cross-section of the bars. This model can numerically simulate the fracture process in structural members of reinforced concrete such as shear wall, beams, plates, etc., mainly when the density of reinforcement makes the modelling of each bar difficult.

Acknowledgements

The authors gratefully acknowledge the financial support provided by the Spanish Ministry of Science and Technology (grants BIA2005-09250-C03-03 and BIA2004-02080). The first author would particularly like to acknowledge the support provided by the DIB, Universidad Nacional de Colombia.

Notation

C^c_tg Tangent constitutive tensor of simple concrete

C_tg: Tangent constitutive tensor of reinforced concrete

d_s,d_s^h: Non-regularised and regularised Dirac's delta functions about discontinuity S,

e^._rr, e^._ss,g^._rs: terms of strain rate tensor of reinforced concrete at plane rs, in engineering notation.

e^._rr, e^._ss,g^._rs: terms of strain tensor of reinforced concrete at plane rs, in engineering notation.

e^ar,e^.ar: Terms of Normal strain and normal strain rate in steel bars orientated in direction r

e^as,e^.as Normal strain and normal strain rate in steel bars orientated in direction

e^a_p,a^a : Plastic strain and internal variables of the slipping bar model

E^a, E^a_tg :Initial and tangent steel elasticity modulus according to the slipping bar model

e^-. : Regular part of the strain rate of reinforced concrete

e^.a : Steel normal strain rate according to slipping bar model

e^.c: Strain rate tensor of simple concrete

e,e^. Strain tensor and strain rate tensor of reinforced concrete

g^a,g^.a Shear strain and engineering shear strain rate of steel

j: Continuous function defined in a band Ω^h inside discontinuity S

G^a, G^a_tg Initial and tangent shear elasticity modulus of the steel

H^a Hardening modulus of the plasticity model applied to the steel

k^c,k^ar,k^as Volumetric participation factors of the concrete matrix, steel bars in r direction and steel bars in s direction

M_s, H_s: Unit jump function and Heaviside's function

n Unit vector normal to discontinuity surface S

W^h Band around discontinuity S of width h

W Domain of a whole solid

W⁺, W^-Sub-domains of a solid split by discontinuity surface S

Q_tg(t_B,n_B) Localisation tensor of reinforced concrete evaluated in bifurcation time and in the direction normal to discontinuity n_B

r Unit vector indicating the orientation of the first parallel bars package bars package

s_y Steel yielding stress to tension or compression

s_adhSteel stress when adherence with concrete has disappeared

s_t^c,s_c^c Simple concrete strength to tension and compression, respectively

S Strong discontinuity surface

s^.ar,s^.as Normal stress rate of the steel bars orientated in direction r and s, respectively.

s^.a Normal stress rate of the steel according to the slipping bar model

s^c Stress rate tensor of simple concrete

s,s^. Stress tensor and stress rate tensor of reinforced concrete

s Unit vector indicating the orientation of the second parallel bars package

t_y Steel shear yielding stress

t^.a Steel shear stress rate

u^-. Continuous part of the displacement rate vector of reinforced concrete

[[u]], [[ü]] Displacement jump vector and displacement jump rate vector of reinforced concrete

u^. Displacement rate vector of reinforced concrete