Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.30 no.2 Bogotá May/Aug. 2010
Lina M. Rangel Martínez1 y Jorge A. Alvarado valencia2
1Ingeniera Industrial. Profesora Catedrática, Facultad de Ingeniería, Departamento de Ingeniería Industrial, Pontificia Universidad Javeriana, Bogotá, Colombia. lrangel@javeriana.edu.co 2 Ingeniero Industrial. M. Sc., en Analytics. Profesor Asistente, Facultad de Ingeniería, Departamento de Ingeniería Industrial, Pontificia Universidad Javeriana, Bogotá, Colombia. jorge.alvarado@javeriana.edu.co
RESUMEN
La reciente aparición de modelos generatrices de líneas de espera con tiempos de atención heavy-tailed y su comprobación empírica implican la necesidad de conocer el comportamiento de las medidas clásicas de desempeño de una línea de espera bajo estas condiciones. El objetivo del estudio fue el de analizar el comportamiento de Lp(longitud promedio de la fila) y Wp(tiempo promedio de espera en fila) variando los parámetros capacidad del sistema, nivel de utilización promedio (r) y número de servidores para líneas de espera con tiempos de atención heavy-tailed, y contrastar dicho comportamiento con los resultados clásicos basados en procesos de Poisson, usando para ello la simulación de eventos discretos. Los resultados mostraron que la sensibilidad de los modelos con tiempos de atención heavy-tailed a variaciones en los parámetros es mayor que la de los modelos basados en procesos de Poisson. En particular, a partir de capacidades de sistema de 1.000 entidades ciertos procesos heay-tailed pueden considerarse infinitos, y la importancia del número de servidores es mayor en los procesos heavy-tailed analizados que en los procesos de Poisson. Por último, la utilización de Lp y Wpcomo medidas de desempeño es inadecuada para tiempos de atención heavy-tailed al generar resultados inestables y contraintuitivos.
Palabras clave: líneas de espera, distribuciones heavy-tailed, tiempos de servicio, distribución de Pareto, modelos generatrices.
ABSTRACT
Recent research showing theoretical generative models for heavy-tailed service time queues and its empirical validation implies the need for a better knowledge of the key performance indicators' behaviour under such assumption. The behaviour of the average length of the queue (Lp) and the average waiting-time (Wp) were analysed through simulation, varying system capacity, average service utilisation factor (r) and the number of servers in the systems as parameters. Comparisons were also made with service times based on Poisson processes. The results showed more sensitive variations of Lpand Wpfor heavy-tailed service times than for Poisson-based service times. Systems having a capacity of over 1,000 entities might be considered as being systems having infinity capacity and the number of servers has a greater importance in heavy-tailed ruled processes than in Poisson processes. There was a lack of adequacy of Lpand Wpas key performance indicators for heavy-tailed service times, leading to unexpected and unstable results.
Keywords: queuing system, heavy-tailed distribution, service time, Pareto distribution, generative model.
Recibido: junio 26 de 2009 Aceptado: julio 10 de 2010
Introducción
La evidencia empírica reciente sugiere que algunas de las distribuciones de probabilidad de tiempos de servicio en líneas de espera no presentan colas exponenciales, y por tanto, obtener valores extremos en tiempos de servicio deja de ser algo improbable (Stidham, 2002).
Ejemplos empíricos de la aparición de este tipo de distribuciones son: el procesamiento y respuesta de correo electrónico (Barabási, 2005), el tiempo de atención en un taller automotriz (Alvarado et al.,2008) y el tiempo de transmisión de un archivo en telecomunicaciones (Mitzenmacher, 2004).
Dos modelos teóricos han sido propuestos para explicar esta situación: el primero sugiere que si el tamaño del trabajo a procesar que llega a la fila es una variable aleatoria con colas no exponenciales (tal es el caso de los archivos en telecomunicaciones), el tiempo de procesamiento de ese trabajo tendrá como consecuencia colas no exponenciales (Willinger, 1995); el segundo plantea que cuando el servidor es un ser humano que debe utilizar su propio criterio para decidir cuál trabajo procesar primero, y no hay seres humanos físicamente en la fila, se genera un fenómeno denominado prioridades percibidas, que lleva a postergar durante largos tiempos el procesamiento de un trabajo que ya ha ingresado al servidor y por consiguiente los tiempos de atención tendrán colas no exponenciales (Barabási, 2005; Alvarado et al., 2008). De lo anterior se deduce la existencia de un importante conjunto de fenómenos que podría ser modelado con más precisión utilizando distribuciones con colas no exponenciales.
Las distribuciones con colas no exponenciales suelen ser denominadas distribuciones heavy-tailed, si bien el uso de esta expresión ha sido algo confuso en la literatura (Embrechts et al., 1997; Mitzenmacher, 2004). Este artículo se ceñirá a la siguiente definición, que expresa de manera clara la naturaleza no exponencial de la cola: dada una variable aleatoria no negativa X, su función de distribución acumulada 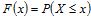 y su función acumulada complementaria, o cola,
y su función acumulada complementaria, o cola, 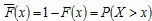 , una función de distribución para la variable aleatoria X, es denominada heavy-tailed si
, una función de distribución para la variable aleatoria X, es denominada heavy-tailed si 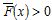 ,y
,y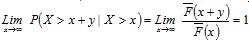 para y≥0(Sigman, 1999, pp. 261-262). En contraste, una cola exponencial presenta el comportamiento
para y≥0(Sigman, 1999, pp. 261-262). En contraste, una cola exponencial presenta el comportamiento 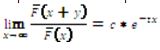 , siendo c y t constantes.
, siendo c y t constantes.
Entre el conjunto de las distribuciones heavy-tailed son ampliamente conocidas las distribuciones de Weibull (en análisis de confiabilidad) y de Pareto (en análisis financiero).
Uno de los mayores desafíos que presentan la mayoría de las distribuciones heavy-tailed para el análisis de líneas de espera es la no convergencia de la media y la varianza. Sin el cumplimiento del supuesto de media y varianza finitas, los resultados clásicos de la teoría de colas para modelos M/G/1/FIFO/CO/CO de Cohen (Cohen, 1973, pp. 343-353) y Pakes (Pakes, 1975, pp. 555-564) no son válidos. Dada la dificultad matemática de las distribuciones heavy-tailed, no se conocen soluciones cerradas para líneas de espera con tiempos de atención heavy-tailed, y sólo hasta años recientes Whitt (Whitt, 2000, pp. 71-87) probó que si el tiempo de servicio tiene una distribución de probabilidad heavy-tailed, la longitud de la fila y el tiempo de espera tendrán también una distribución heavy-tailed, con cotas superior e inferior para estos valores bajo ciertos parámetros, resultado válido sólo para los sistemas M/G/1/FIFO/∞/∞.Basados en estos antecedentes, la investigación tuvo como objetivo simular numéricamente el comportamiento de un modelo de líneas de espera donde el tiempo de atención esté regido por una distribución heavy-tailed bajo diversas condiciones de capacidad del sistema, utilización y número de servidores para analizar las variaciones de sus medidas de desempeño y la viabilidad misma de estas medidas (longitud promedio de la fila Lpy tiempo promedio de espera Wp).
Para facilitar el logro de este objetivo los resultados se compararon con los obtenidos para el modelo clásico de líneas de espera con tiempos de atención basados en procesos de Poisson.
Desarrollo experimental
El experimento utilizó simulación de eventos discretos, que es una buena alternativa cuando no se conocen aproximaciones o resultados cerrados para una línea de espera y se desea realizar un análisis exploratorio del modelo bajo rangos significativos de sus parámetros (Neuts, 1998; Stewart, 1994; Gross, 2009), como es el caso aquí analizado. La evaluación sistemática de variaciones en los factores que influyen en un fenómeno evaluados en un experimento controlado como es la simulación se suele llevar a cabo de manera eficiente mediante un diseño experimental estadístico (Kuehl, 2001).
Diseño experimental
Entre los factores que la teoría clásica de líneas de espera considera fundamentales en el análisis se escogieron para este trabajo la distribución de los tiempos de servicio, la capacidad del sistema, el nivel de utilización y la cantidad de servidores. La disciplina de la fila no se tuvo en cuenta por considerarse que estaba implícita en el modelo de prioridades percibidas, explicado en la introducción para tiempos de atención heavy-tailed. El número de clientes potenciales del sistema se mantuvo infinito, pues hacerlo finito tan sólo lograría limitar y enmascarar el efecto que la distribución heavy-tailed tendría sobre la longitud de la fila y el tiempo de espera. En cuanto a la distribución de probabilidad de los tiempos de llegada, se mantuvo la utilización de un proceso de Poisson para hacer más comparables los resultados con las ecuaciones cerradas de la teoría clásica de líneas de espera. Los factores y niveles definidos generaron un modelo mixto con tres factores fijos o constantes y uno aleatorio (los parámetros de las distribuciones), cuya combinación daba lugar a 1.575 posibles tratamientos. Se decidió realizar un experimento factorial completo dado que la capacidad computacional no era una limitación y ello permitía el análisis exploratorio más amplio posible.
Parámetros de las distribuciones de probabilidad de los tiempos de servicio
Se seleccionó como paradigmática de las distribuciones heavy-tailed la distribución de Pareto por ser una de las distribuciones de esta clase más conocidas y utilizadas, y por tener la importante propiedad de que dependiendo de los valores de sus parámetros, su media y su varianza pueden o no converger, lo cual permite una exploración más amplia de los efectos de las distribuciones heavy-tailed (Andriani y McKelvey, 2005, pp. 219-223). La distribución Pareto tiene la siguiente distribución de probabilidad:
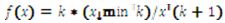 para
para 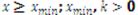
Siendo Xminun parámetro de posición (mínimo de la función) y k el parámetro de forma, cuyo valor determina si tanto la media como la varianza convergen: en el rango 0,1;tanto la media como la varianza divergen, en 0,2 la media diverge pero la varianza no, y en (2,∞)ambos valores convergen (Mitzenmacher, 2004, pp. 228).
Así mismo, cuanto mayor sea el valor de k se tendrán densidades de Pareto más concentradas en las proximidades del mínimo, es decir, densidades menos dispersas (Newman, 2005, pp. 325-327).
La función de probabilidad cumple con la condición de colas no exponenciales, puesto que su cola se rige por la expresión
Pr (X>x)=(x/xm)x
El interés se centró en determinar si existían variaciones importantes de Lpy Wpasociadas a la convergencia de la media y la varianza de una distribución heavy-tailed, por lo que se generaban tres intervalos de interés en la distribución Pareto, en los cuales se seleccionó aleatoriamente un punto que representara cada uno de los niveles de interés de la investigación, como se explica a continuación.
Primero, se estableció una relación entre la distribución exponencial (proceso de Poisson) y la distribución Pareto de manera tal que alguna de sus medidas de tendencia central diferente de la media fuese equivalente. Se decidió utilizar la mediana por ser una medida de tendencia central robusta. Siendo la mediana de la distribución exponencial b*lim(2)(Ross, 2006, p. 419) y la mediana de la distribución Pareto Xminx√2(Janicki y Simpson, 2005, p. 294), se realizó la siguiente equivalencia:
b*lim(2)-Xminx√2
De donde se obtiene la ecuación de equivalencia:
k=ln (2*Xmin/ b*ln (2))
En segundo lugar, se estableció una tasa media de servicio fija para todo el sistema µ con valor unitario, por lo que μ
En tercer lugar, y a partir de los rangos de convergencia de la distribución Pareto y la ecuación de equivalencia, se formaron rangos de convergencia basados en el parámetro b=1/μ = 1.
Por último, se generó un número aleatorio dentro de cada rango de convergencia de Xminy se establecieron estos tres valores como niveles aleatorios para el factor parámetro de la distribución del tiempo de servicio, obteniendo los valores para k a partir de la ecuación de equivalencia.
Número de servidores
Se realizaron variaciones en el rango de 1 a 15 servidores, tomando como referencia la propuesta mostrada en el texto bibliográfico de Hillier y Lieberman para modelos sin entradas Poisson (Hillier y Lieberman, 2005, pp. 802). De acuerdo con ello, los niveles seleccionados fueron: 1, 2, 3, 5, 7, 10 y 15 servidores.
Capacidad del sistema
La capacidad del sistema puede ser considerada como finita o infinita. Para definir los niveles del factor se hizo una transferencia de metodologías utilizadas en otras ciencias, como la neurociencia y la física, cuyos ámbitos de dominio y escalas de observación varían de acuerdo con potencias de 10. De esta manera, los niveles para la capacidad finita variaron desde 10 entidades (103) para un sistema pequeño, hasta 10.000 entidades (104). Se consideró que potencias superiores a cinco entrarían, para efectos prácticos, dentro de la categoría de servicios sin capacidad limitada.
Factor promedio de utilización del servicio ()
Los valores de este factor se variaron en el rango (0, 1) para abrir la posibilidad de alcanzar el estado estable.
En el rango que se definió, se estableció un salto constante de 0,2, obteniéndose 5 niveles para este factor.
Simulación
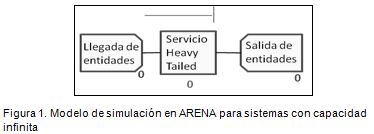
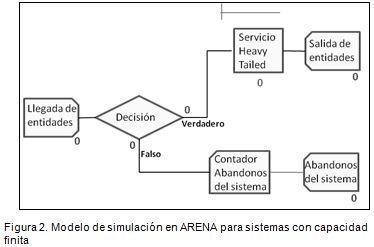
Todo modelo de línea de espera se representa por medio de tres instancias básicas: una fuente de generación de entidades que representa la llegada de éstas al sistema, un conjunto de servidores que atienden a las entidades, sobre los cuales se genera la cola, y una salida por donde se despachan las entidades una vez han sido atendidas. Considerando esta estructura, se realizaron los modelos para ser simulados (Figura 1). Adicional a esta estructura, se agregó una validación relacionada con la capacidad del sistema para restringir la entrada de entidades una vez éste se ha copado (Figura 2).
No se encontró literatura disponible que permitiese estimar un tamaño de muestra mínimo para un experimento con tres factores fijos con diferente cantidad de niveles y un factor aleatorio. La complejidad misma de definir tamaños de muestra adecuados cuando se presentan factores aleatorios es bien conocida (Montgomery, 2008). Se decidió realizar el mayor número de réplicas que el tiempo y la capacidad computacional permitieran. Puesto que los tamaños de muestra para diseños con cuatro factores fijos no superan las 1.000 unidades en los casos asintóticos (Kuehl, 2001), se consideró que la realización de 10.000 réplicas para cada uno de los 1.575 tratamientos daría un margen de seguridad suficiente para los resultados.
Con respecto a la duración de cada una de las réplicas, se buscó representar un mes de trabajo continuo en una empresa, es decir, 30 días de 24 horas, para un total de 720 horas/mes. Buscando una mayor precisión para el experimento, se aproximó este valor a 1.000 horas/réplica
Resultados
El análisis de los resultados arrojados para la prueba de análisis de varianza realizada en el experimento diseñado permite establecer la existencia de diferencias entre las medias de los factores.
Se encontraron interacciones significativas (valor p<0,001) entre los factores listados a continuación. Interacciones de segundo orden se encontraron entre: capacidad y número de servidores; capacidad y nivel de utilización; número de servidores y nivel de utilización. Se encontró interacción de tercer orden entre capacidad, servidores y nivel de utilización; e interacción de cuarto orden entre capacidad, servidores, nivel de utilización y parámetros de la distribución Pareto.
El análisis hecho para identificar el sentido de las interacciones es descriptivo, siempre y cuando la interacción como tal sea significativa desde un punto de vista estadístico.
Variaciones generales en las medidas de desempeño
Suponer distribuciones exponenciales de los tiempos de servicio lleva a una subestimación del verdadero valor de Lpy Wpsi en realidad el proceso presenta tiempos de atención heavy-tailed. Por ejemplo, para una línea de espera con capacidad finita, el máximo valor promedio alcanzado de Lpfue 98 entidades, mientras que con una distribución heavy-tailed bajo las mismas condiciones del sistema anterior, este valor ascendió a 437 entidades: un incremento del 345%.
En el caso Wpel valor promedio máximo alcanzado con capacidad finita es de 99 horas, mientras que con una distribución heavytailed bajo las mismas condiciones del sistema, este valor asciende a 273 horas: un incremento del 175%.
Efectos debidos a la capacidad del sistema
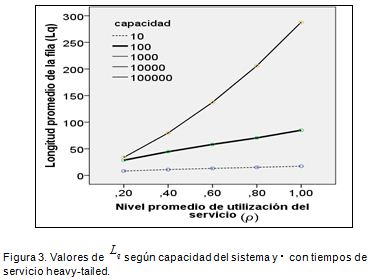
Al realizar modificaciones en la cantidad de servidores disponibles en un sistema o en su nivel de utilización, se encuentra que los valores de Lpno varían en sistemas con capacidades superiores a 100 entidades cuando se tienen tiempos de servicio heavy-tailed, es decir, que los sistemas con capacidades superiores a este valor, bajo esta distribución, pueden ser considerados como de capacidad infinita (Figura 3).
Esta situación ocurre igualmente para Wp pero solo cuando el factor de utilización es inferior a 0,6. Por encima de este valor, los resultados pierden estabilidad.
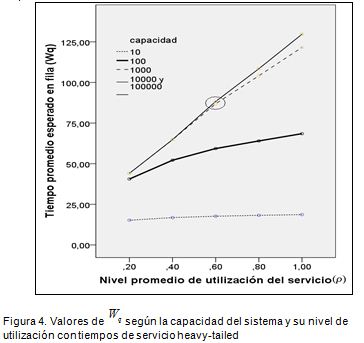
En la Figura 4 se observa una tendencia de crecimiento prácticamente lineal para Wp.
Para una capacidad de 10 entidades, el cambio de Wpal pasar de un sistema con r=0.2a uno con un nivel de utilización muy cercano a 1 es del 22%, mientras que para un sistema con capacidad infinita es de 194%.
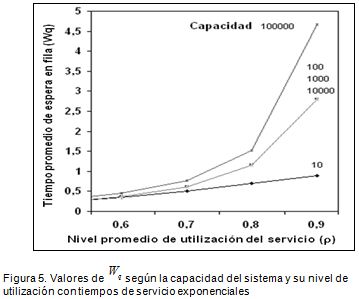
Caso contrario sucede en los sistemas con tiempos de servicio exponenciales, donde un sistema con capacidad para 10.000 entidades no puede ser considerado como infinito, pues Lpy Wptoman valores diferentes frente al sistema con 100.000 entidades (Figura 5). La tasa de crecimiento de Wpes mayor que en los sistemas heavy-tailed (compárese la forma de las figuras 4 y 5). Sin embargo, los valores de Lpy Wpen sistemas exponenciales es menor que en sistemas heavy-tailed.
Efectos debidos al número de servidores
Al aumentar la cantidad de servidores del sistema utilizando la distribución exponencial en los tiempos de servicio, los valores de Lpse reducen excepto en niveles de utilización altos, donde se pierde el estado estable. Estos resultados son los esperados de acuerdo a la teoría.
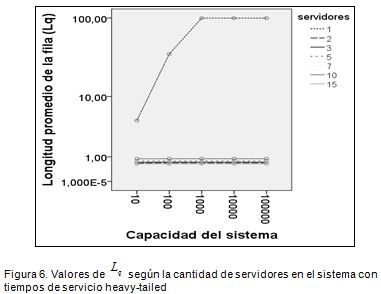
Para el caso de las distribuciones heavy-tailed se observa un comportamiento atípico cuando se tiene un único servidor en el sistema (Figura 6), pues sólo con aumentar a dos servidores, el valor de Lpse reduce en gran proporción y no varía de allí en adelante al aumentar el nivel de utilización. Esto implicaría que si se tienen distribuciones heavy-tailed importa menos el nivel de utilización del sistema, ganando relevancia la cantidad de servidores disponibles en él.
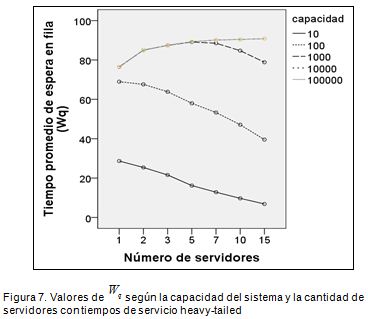
Cuando se tienen capacidades superiores a 1.000 entidades en sistemas con tiempos de servicio heavy-tailed , Wpno disminuye consistentemente como sería de esperarse al aumentar el número de servidores, sino que presenta un comportamiento contraintuitivo. Como puede apreciarse en la Figura 7 el valor de Wpse incrementa entre 1 y 5 servidores. Para una capacidad de 1.000 entidades, a partir de 5 servidores Wpcomienza a disminuir; para más de 1.000 entidades, el aumento atípico de Wpse mantiene.
Este comportamiento atípico en sistemas con distribuciones heavy-tailed puede ser consecuencia de la no convergencia de su media o varianza para ciertos valores.
Efectos debidos al factor de utilización r
En la medida en que aumenta el nivel de utilización del sistema, se incrementan de forma acelerada Lpy Wp, con independencia de la distribución de los tiempos de servicio, como era de esperar. Para capacidades mayores, se hacen más evidentes las variaciones de Lpy Wpconforme crece r .
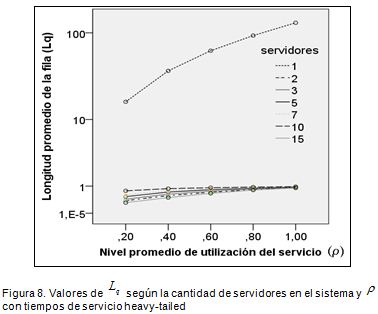
En sistemas con tiempos de servicio exponenciales los valores de Lpse hacen realmente representativos, es decir, mayores a una entidad, para niveles superiores a 0,7, independientemente de la cantidad de servidores en el sistema y su capacidad. Para los sistemas con distribuciones heavy-tailed las variaciones del indicador son representativas, y mayores a las obtenidas con tiempos de servicio exponenciales, desde un nivel de utilización de 0,2 únicamente cuando el sistema tiene 1 servidor (Figura 8), de manera similar a lo mostrado en la sección anterior, lo cual representa un comportamiento atípico. De 2 servidores en adelante los valores y variaciones de Lpson mínimas y no significativas.
Se encontró que en la medida en que se incrementa la capacidad del sistema junto con el nivel de utilización, no se desestabiliza el sistema en cercanías a un nivel P = 1para distribuciones de los tiempos de servicio exponenciales, mientras que con tiempos de servicio heavy-tailed el comportamiento de desestabilización se sigue presentando. Esto evidencia cómo los sistemas con distribuciones exponenciales son más predecibles y arrojan resultados más confiables con niveles de utilización y capacidades elevados.
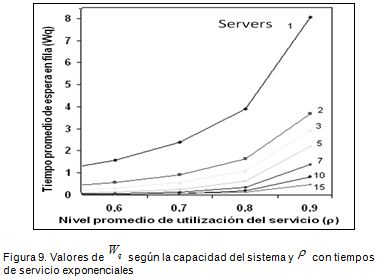
Las variaciones de Wpal incrementar el nivel de utilización del sistema de 0,2 a 1 se hacen cada vez más pequeñas en la medida en que se aumenta la cantidad de servidores disponibles en el sistema, hasta llegar a ser nulas para 15 servidores (Figura 9).
Este comportamiento evidencia que en sistemas con pequeñas capacidades el tiempo promedio que una entidad espera en la fila antes de ser atendida parece no depender de la tasa de llegada de entidades al sistema ni de la tasa de servicio.
Efectos debidos a los parámetros de la distribución
Las mayores variaciones de Lpy Wpdependen del nivel de utilización de los sistemas con tiempos de servicio exponenciales, más que de la capacidad del sistema y el número de servidores;
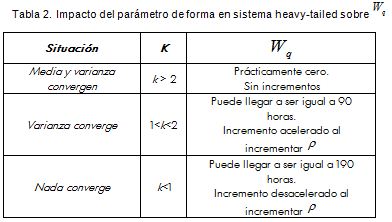
mientras que para sistemas con tiempos de servicio heavy-tailed, es el parámetro de forma (k) el que determina la magnitud de la variación, es decir, la convergencia de la media o de la varianza (Tablas 1 y 2).

Conclusiones
La investigación mostró que las medidas de desempeño clásicas de las líneas de espera presentan comportamientos atípicos e inestables cuando la distribución de los tiempos de atención tiene un comportamiento heavy-tailed. Esto puede deberse tanto a la tendencia de las distribuciones heavy-tailed a generar valores extremos con mayor frecuencia como a la no convergencia de la media o la varianza de la distribución heavy-tailed. De este modo se concluye que los indicadores basados en promedios tales como Lpy Wpno son los más adecuados para medir el desempeño de una línea de espera cuando la distribución de los tiempos de servicio es heavy-tailed. Puesto que los modelos generatrices teóricos de distribuciones heavy-tailed presentados en la introducción cubren una amplia gama de situaciones reales, es necesario para investigadores y profesionales considerar la posibilidad de la presencia de modelos heavy-tailed cuando se presenten valores extremos en las muestras, en vez de simplemente hallar una explicación para ellos y posteriormente, descartarlos.
Trabajos futuros pueden explorar nuevos y más robustos indicadores para líneas de espera cuyos tiempos de servicio puedan ser modelados con variables heavy-tailed.
Otro resultado clave de la investigación es la mayor sensibilidad de las distribuciones heavy-tailed a cambios en los parámetros tales como la capacidad del sistema y el número de servidores, lo cual debe tenerse en cuenta al momento de tomar decisiones en líneas de espera con tiempos de atención heavy-tailed. La realización de un análisis de riesgo en la toma de decisiones bajo estas condiciones es otra vía de investigación que se abre.
Apéndice: nomenclatura
Lp: Longitud promedio de la fila
Wp: Tiempo promedio de espera en fila
r : Nivel promedio de utilización
Xmin: Parámetro de posición de la distribución Pareto
k: Parámetro de forma de la distribución Pareto
b: Parámetro de la distribución exponencial
Bibliografía
Alvarado, J. A., Montoya, J. R., Rangel, L. M., Analyse par simulation de l'impact de la modélisation du temps de service avec une distribution heavy-tailed: étude de Cas d'un atelier de maintenance automobile., Mosim 2008, Proceedings of the 7eme conference international de modelisation et Simulation, Paris, 2008. [ Links ]
Andriani, P., McKelvey, B., Why Gaussian statistics are mostly wrong for strategic organization., Strategic Organization, Vol. 3, 2005, pp. 219–223. [ Links ]
Barabási, A. L., The origin of bursts and heavy-tailed in human dynamics., Nature, Vol. 435, 2005, pp. 435–439. [ Links ]
Cohen, J. W., Some results on regular variation for distributions in queuing and fluctuations theory., Journal of Applied Probability, Vol. 10, 1973, pp. 343–353. [ Links ]
Embrechts, P., Kluppelberg, C.,Mikosch, T., Modeling extremal events for Insurance and finance., New York, Springer-Verlag, 1997. [ Links ]
Gross, D., Fundamentals of queuing theory., 4th ed., New York, John Wiley & Sons, 2009. [ Links ]
Hillier, F., Lieberman, G. J., Operations Research., 8th ed., México, McGraw-Hill. 2005. [ Links ]
Janicki, H. P., Simpson, E., Changes in the size distribution of US Banks: 1960–2005., Economic Quarterly - Federal Reserve Bank of Richmond, Vol. 92, No. 4, 2005, pp. 291-316. [ Links ]
Kuehl, R., Diseño de experimentos: Principios estadísticos de diseño y análisis de investigación., México, International Thomson Editores, 2001. [ Links ]
Mitzenmacher, M., A brief history of generative models for power law and lognormal distributions., Internet Algorithms, Vol. 1, No. 2, 2004, pp. 226–251. [ Links ]
Montgomery, D., Design and analysis of experiments., 7th edition, 2008, Wiley. [ Links ]
Neuts, M. F., Computer experimentation in applied probability., Journal of applied probability, Vol. 25A,1988, pp. 31-43 [ Links ]
Newman, M., Power laws, Pareto distributions and Zipf's law., Contemporary Physics, Vol. 46, 2005, pp. 323-351. [ Links ]
Pakes, A. G., On the tails of waiting-time distributions., Journal of Applied Probability, Vol. 12, 1975, pp. 555–564. [ Links ]
Ross, S., A first course in probability., 7th ed., New Jersey, Pearson Prentice Hall, 2006. [ Links ]
Sigman, K., Apendix: A primer on heavy-tailed distributions., Queuing Systems, Vol. 33, No. 1-3, Dic., 1999, pp. 261–275. [ Links ]
Stidham, S., Analysis, Design, and Control of Queuing Systems., Operation research, Vol. 50, 2002, pp. 197-216. [ Links ]
Stewart, W. J., Introduction to the numerical solution of Markov chains, New Jersey, Princeton University Press, 1994. [ Links ]
Whitt, W., The impact of a heavy-tailed service-time distribution upon the M/GI/s waiting time distribution., Queuing Systems, Vol. 36, 2000, pp. 71-87. [ Links ]
Willinger, W., Traffic modelling for high-speed networks: theory versus practice., Stochastic Networks, IMA Volumes in Mathematics and its applications 71, Springer-Verlag, New York, 1995, pp.169-181. [ Links ]











 text in
text in 


