Fredy Orlando Ruiz Palacios¹y Carlos Eduardo Cotrino Badillo²

¹Ingeniero Electrónico, Pontificia Universidad Javeriana (PUJ), Bogotà, Colombia. M. Sc., Universidad Javeriana (PUJ), Bogotá, Colombia. Ph.D., en Investigación, Politecnico di Torino, Italia. Profesor Asistente, Pontificia Universidad Javeriana (PUJ), Bogotá, Colombia. ruizf@javeriana.edu.co ² Ingeniero Electrónico, Pontificia Universidad Javeriana, Bogotá, Colombia. M Sc, SUNY at Stony Brook. Profesor Asociado, Pontificia Universidad Javeriana (PUJ), Bogotá, Colombia. ccotrino@javeriana.edu.co

RESUMEN

En este trabajo se presenta el desarrollo de un modelo dinámico del clima en un invernadero ubicado en la Sabana de Bogotá. Se realiza la estimación de un modelo tipo caja negra obtenido a partir de datos experimentales. Se propone una estructura a partir de principios físicos que divide el sistema en dos volúmenes de control dados por el aire libre dentro del invernadero y el aire atrapado por el follaje. El modelo es seleccionado, dentro de una familia de sistemas líneales descritos en variables de estado, a través de métodos de identificación por subespacios. El modelo obtenido es capaz de explicar el comportamiento del clima en el aire y en el follaje con errores inferiores al 8%. Este desempeño es comparable al de otros estudios reportados en la literatura, con la ventaja de que el modelo empleado es lineal.

Palabras clave: estimación paramétrica, identificación por subespacios, dinámica del clima en invernaderos.

ABSTRACT

This paper presents the development of a climate dynamics model for a greenhouse located on the Bogota plateau. A black-box model was estimated from experimental data, considering a novel system structure derived from a first principles model and experimental tests. It considered two control volumes, one given by the air over the crop and a second one formed by the air trapped by crop foliage. The model was selected from a set of linear, discrete-time, statevariable systems using subspace identification methods. The estimated system was able to predict climate dynamics for both control volumes, having errors below 8%. Such performance was comparable to previous work reported in literature while the obtained model was a low-complexity linear system

Keywords: parametric estimation, subspace identification, greenhouse climate model.

Recibido: noviembre 24 de 2009 Aceptado: mayo 11 de 2010

Introducción

A pesar de la antigüedad de la actividad agrícola, sólo en las últimas décadas se han utilizado sistemas de información y control automático para optimizar la calidad y la productividad de las cosechas. En particular, desde los años sesenta se han estudiado estrategias de control para optimizar la producción de cultivos bajo invernadero y se han planteado modelos dinámicos que permiten predecir el comportamiento del clima dentro del invernadero. Estos estudios se han llevado a cabo principalmente en Europa, donde las temperaturas extremas que se presentan en invierno y verano hace necesario optimizar el costo de operación de los sistemas de calefacción y aire acondicionado empleados para no someter a las plantas a temperaturas extremas y posiblemente dañinas. En la Universidad de Wageningen, G. P. Bot ha desarrollado mo-delos dinámicos de invernaderos ubicados en Holanda, a partir de procesos biológicos (Bot, 1983). Adicionalmente, se han estudiado regímenes climáticos para ahorrar energía en los sistemas de con-trol (Bot, 2001; Körner, 2003; Tap et al., 1996). P. F. Martínez, de la Universidad Politécnica de Valencia, ha evolucionado métodos de identificación de invernaderos sometidos a clima mediterráneo empleando algoritmos genéticos para encontrar los parámetros de un modelo físico altamente no lineal (Herrero et al., 2003).

El Ghoumari (Ghoumari, 2003) presenta un sistema de control predictivo no lineal manejando restricciones. El modelo de clima fue desarrollado desde principios físicos y calibrado mediante Sequiential Quadratic Programming.

Peter Young, de Lancaster University, ha desarrollado métodos estadísticos de identificación y control (Young et al., 2001; Young et al., 1994), y los ha aplicado en el control automático del clima en invernaderos en Bedford, Reino Unido.

En este artículo se presenta una nueva metodología para la construcción del modelo dinámico del clima en invernaderos. El modelo es estimado dentro de un conjunto de sistemas lineales e invariantes con el tiempo, a partir de datos experimentales. Los resultados obtenidos, determinados como el error entre las señales medidas y la predicción hecha por el modelo, indican que un modelo lineal de tercer orden es capaz de describir la dinámica del clima con una precisión cercana a la lograda con modelos no lineales que tienen en cuenta los fenómenos físicos que condicionan la evolución del sistema, pero con una estructura de baja complejidad.

Configuración experimental

El invernadero estudiado se encuentra en El Rosal (Cundinamarca), a una altura de 2.586 msnm y una temperatura media anual de 14 °C. Tiene unas dimensiones de 77 m de largo por 82 m de ancho; una altura de 2,9 m en los extremos y 4,3 m en la parte central. El área es de 6.314 m² y el volumen de 23.000 m³. La ventilación lateral es variable manualmente y la ventilación cenital fija cubre un área de 370 m², 5,6% del área total de la estructura. La cubierta es de polietileno semitransparente (Figura 1).

El invernadero no presenta variables manipulables, y el estudio se enfoca en la construcción de un modelo del efecto de las perturbaciones (clima exterior) sobre el clima dentro del invernadero.

Para medir y almacenar las variables ambientales se utilizaron equipos Spectrum Technologies - WatchDog 450; con precisiones de +/- 0,6 °C y +/- 3% HR para la temperatura y humedad relativa. La radiación solar se midió con un equipo Spectrum Technologies - PAR Quantum Sensor. Se mide la radiación PAR entre 400 y 700 nm y esta medida se transforma en flujo de energía en el espectro completo (W/m²), transformación posible porque el espectro característico de la luz solar es bien conocido (Kania et. al., 2002; Wang et. al., 2000).

Dentro del invernadero se instalaron cuatro instrumentos de medida para registrar temperatura y humedad del aire, ubicados a 2,5 m del suelo y en posiciones equidistantes dentro del recinto. Otros cuatro instrumentos fueron instalados dentro del follaje, a 1,2 m del suelo, a lo largo de una línea de siembra. Durante el experimento las ventanas laterales permanecieron abiertas un 50%, punto normal de operación del invernadero. Para medir las condiciones ambientales en el exterior se instaló un equipo de registro en un punto de la finca alejado de las construcciones, para evitar la influencia en la medida de fuentes de calor o humedad que alteren las condiciones de medida. Este sistema se ubicó a 1,5 m del suelo.

El intervalo de muestreo se fijó en cinco minutos en todos los experimentos. Este período se seleccionó con base en la velocidad de respuesta de los instrumentos y los tiempos usados por otros autores (Cunha et al., 1997; Körner et al., 2004; Salgado et al., 2005; Wang et al., 2000).

Para realizar el proceso de identificación es necesario acondicionar las señales al formato requerido, empleando los siguientes procedimientos:

 Transformar la humedad relativa a humedad absoluta, necesario para plantear la ecuación de conservación de masa de agua en términos de la humedad absoluta, Χ y no de la relativa, HR, que es función no lineal de la temperatura y de la humedad absoluta.

Este paso desacopla la medida de humedad de la temperatura.

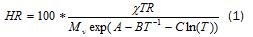
T es la temperatura en Kelvin, R es la constante universal de los gases, M_ves el peso molecular del agua, A, B y C son constantes.

 Para realizar una aproximación de parámetros concentrados, en el proceso de identificación se emplea el promedio de las medidas de temperatura y humedad de los cuatro puntos medidos a nivel de aire.

 Dado que se usa un medidor de radiación PAR (Q_par), es necesario obtener la potencia radiada en el espectro completo (Q_rad). Para esto se usa la hipótesis de que toda la radiación proviene del sol, válida porque no existe iluminación artificial en el invernadero.

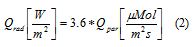
3.6 es un factor de escala con las unidades adecuadas, (Kania et al., 2002).

Selección del modelo

Esta sección describe un modelo de parámetros concentrados y la estructura de los modelos usados en el proceso de identificación de invernaderos.

Modelo teórico

Para describir los procesos climáticos internos del invernadero se construyen modelos a partir de las leyes de conservación de energía y masa. En sentido estricto, la evolución del clima en cada punto del invernadero es diferente y por lo tanto es un sistema de parámetros distribuidos, descrito por ecuaciones diferenciales parciales con condiciones de frontera dadas por cada interfaz con el medio exterior (Molina-Aiz, F., 2004). Sin embargo, un modelo de este tipo genera un sistema de infinitas dimensiones, de alta complejidad, y que no es útil para realizar análisis interpretativos ni para el diseño de sistemas de control.

Asumiendo una temperatura uniforme dentro del invernadero T_m, el volumen de control, delimitado por el aire encerrado en el invernadero, presenta la siguiente ecuación de conservación de energía:

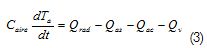(3)

Donde C_airees la capacidad térmica del aire del invernadero; Q_radel flujo de energía proveniente de la radiación solar; Q_asel flujo de calor debido al gradiente térmico existente entre el aire y el suelo; Q_acel flujo de calor a través de la cubierta, generado por el gradiente térmico entre el aire exterior y el interior; y Q_vel flujo de calor debido al intercambio de aire entre el interior y el exterior.

Para el modelo de temperatura del suelo se define un segundo volumen de control. Éste se toma como una capa de tierra que interactúa con el aire y con el subsuelo (Bot, 1983). La ecuación para la temperatura del suelo T_mes:

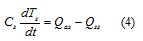
Donde C_mes la capacidad térmica del suelo y Q_sses el flujo de calor debido al gradiente térmico entre el suelo y el subsuelo. Este modelo considera que el subsuelo es una variable de entrada, no manipulable, y que evoluciona de manera independiente al clima del invernadero.

La humedad absoluta Xes la cantidad de vapor de agua presente en el aire, medida como masa de vapor de agua por unidad de volumen; y su comportamiento en un volumen limitado se describe a partir del balance de masa de vapor de agua en la frontera del volumen (Tap, 1996):

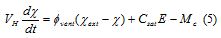
donde V_mes el volumen efectivo del invernadero; Φ_aire(X_ΔXΔ-X)es el flujo de vapor de agua hacia o desde el exterior; E es la transpiración del cultivo generada por fenómenos biológicos; C_airees la constante de saturación de agua en el aire y M_ces la condensación de vapor en las paredes del invernadero y en las hojas del cultivo.

(3), (4) y (5) conforman un sistema de ecuaciones diferenciales no lineales acopladas y son la formulación en variables de estado del clima dentro del invernadero.

La dificultad de la formulación de un modelo teórico para un invernadero específico radica en la complejidad de estimar cada

uno de los términos que forman el sistema de ecuaciones, ya que cada uno de los flujos de calor y de vapor de agua es descrito por una función no lineal de las condiciones climáticas internas y externas, parametrizada por la geometría del invernadero, el tipo de siembra y otros factores biológicos.

Modelo paramétrico

En esta sección se construye, a partir de datos experimentales, un modelo dinámico lineal, en tiempo que describe el clima en el invernadero. El modelo se parametriza como un único sistema dinámico de múltiples entradas y salidas en variables de estado, debido a que se dispone de métodos de identificación eficientes y robustos para este tipo de sistemas.

El modelo está formado por un conjunto de ecuaciones diferencia de primer orden:

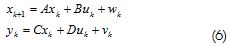
donde k es la variable independiente tiempo, w_k∈R''el vector de las m entradas del proceso en el instante k, y_k∈R'el vector de las l salidas del proceso en el instante k,x_k∈R' el vector de las n variables de estado del proceso en el instante k, y w_k∈R' y v_k∈R'son las señales vectoriales estocásticas, no medibles, que representan el ruido de proceso y la medida del sistema. Se asume que son secuencias vectoriales de ruido blanco, estacionarias y de media cero, con:

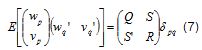
Las matrices A,B,C,Dparametrizan el modelo, Q,R,Sson las matrices de covarianza de las secuencias de ruido. Estas siete matrices deben ser estimadas a partir de los datos experimentales disponibles.

Selección de variables

Aunque la mayoría de autores consideran que el ambiente dentro del invernadero es uniforme verticalmente (Bot, 1983; Herrero et al., 2003; Piñón et al., 2002; Trigui et al., 2001), para este invernadero se encontró que se manifiestan gradientes importantes entre el aire que se encuentra cerca a las plantas y el aire sobre el cultivo.

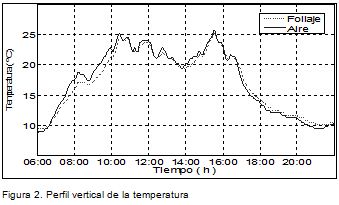
La Figura 2 muestra el comportamiento de la temperatura en un punto del invernadero. El aire cercano al follaje presenta un retardo, tanto en el calentamiento como en el enfriamiento. Además los cambios rápidos de temperatura que sufre el aire superior son atenuados dentro del follaje. Estos dos elementos sugieren la hipótesis de que el follaje tiene un efecto de filtro pasa bajo que aumenta el orden del sistema.

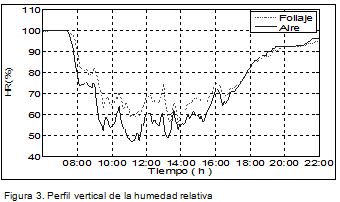
El comportamiento de la humedad es diferente, el follaje siempre exhibe una humedad mayor a la del aire, causada por la evapotranspiración de las plantas. Las variaciones temporales son similares en los dos puntos. No se puede decir que la humedad en el follaje sea una versión filtrada de la humedad del aire, más bien, es

es la misma señal con un desplazamiento que varía con las condiciones ambientales. La evapotranspiración del cultivo es el flujo de agua hacia el am-biente en forma de vapor. Cuando el déficit de presión de vapor se acerca a cero la hoja no emite vapor al aire. Este comportamiento es coherente con el comporta-miento observado en el experimento (Figura 3).

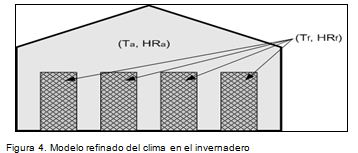
Aunque existen gradientes importantes en dirección vertical, es viable una aproximación de parámetros concentrados. Para ello se propone un modelo compuesto por dos volúmenes de control (Figura 4). El primero es el aire atrapado en el invernadero fuera del follaje y corresponde al aire interior usado en la mayoría de aproximaciones. El segundo volumen corresponde al aire encerrado por el follaje. En la interfaz entre los dos volúmenes ocurren intercambios de calor por conducción y convección y flujos de masa de vapor de agua a causa de gradientes de presión parcial. La estructura del modelo a identificar es la siguiente:

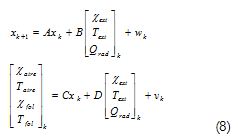
Las entradas del sistema son la temperatura externa T_aire, la humedad absoluta externa X_airey la radiación solar Q_rad. Las salidas son la temperatura T_airey humedad X_airedel aire dentro del invernadero y la temperatura T_foly humedad X_folatrapada por el follaje.

Dado que el comportamiento del microclima dentro del follaje depende considerablemente del tipo de siembra y la variedad de flor que se encuentre plantada, la temperatura y la humedad del aire dentro del follaje, se toma un punto y se usa directamente en el proceso de identificación. Adicionalmente, este enfoque se justifica porque el modelo físico indica que la relación es unidireccional, el clima del aire sobre el cultivo afecta el microclima del follaje, pero, como el volumen de aire encerrado es mucho menor que el volumen total del invernadero, la influencia en sentido inverso es despreciable.

Resultados experimentales

Para la identificación del modelo del clima usando la estructura planteada en (8), se tomaron dos conjuntos de datos durante diferentes días. El primero, llamado conjunto de identificación, está compuesto por 1.650 muestras de cada variable, tomadas durante 138 horas continuas. Este conjunto se emplea para estimar el orden del sistema n y las matrices A, B, C y D. El segundo, denominado conjunto de validación, contiene 860 muestras de cada variable, tomadas durante 72 horas continuas. Este conjunto es usado para medir la calidad de los modelos estimados, comparando su capacidad explicativa con datos que no fueron empleados para su construcción.

Estimación del orden

En la identificación por subespacios (Overchee et al., 1996), el orden del sistema a identificar corresponde a los valores singulares no nulos de la proyección oblicua del subespacio generado por las salidas futuras y paralelo al subespacio de las entradas futuras, sobre el espacio de las entradas y salidas pasadas. De manera intuítiva, la dimensión de este subespacio corresponde a la información de las salidas futuras que no puede ser explicada por las entradas futuras y que por lo tanto depende de las entradas y salidas pasadas. La Figura 5 muestra los valores singulares obtenidos para el conjun-to de identificación. Este resultado sugiere que el orden del siste-ma que ha generado los datos es n=3.

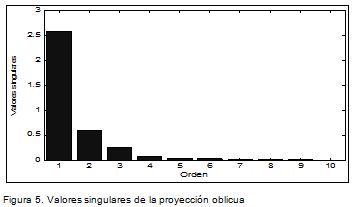
El modelo físico descrito en la sección anterior y los experimentos preliminares también sugieren un orden n=3, dos ecuaciones diferenciales para el comportamiento del aire sobre el cultivo y una más para el comportamiento de la temperatura del follaje, que resulta ser una versión filtrada de la temperatura del aire superior. La humedad dentro del follaje presenta una dinámica muy similar a la del aire superior, pero con un desplazamiento variable que depende de la temperatura, del déficit de presión de vapor y de la radiación solar.

Comportamiento del modelo

Empleando el algoritmo por subespacios robusto para identificación combinada determinística-estocástica propuesto por Overchee et al. (1996), se identifica un modelo de orden 3.

Para medir la calidad del modelo se usa el error porcentual de simulación:

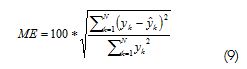
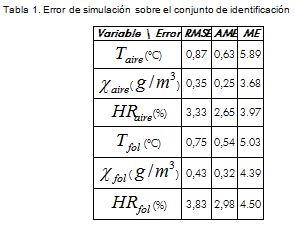
donde Y_kes la salida del sistema físico, Y^-_kes la salida estimada por el modelo identificado y N es la duración del experimento.La Tabla 1 resume el comportamiento del modelo estimado sobre el conjunto de identificación. En ésta, además del ME, se incluyen los errores cuadrático medio (RMSE) y absoluto medio (AME).

El error porcentual obtenido es inferior al 6% para todas las variables estimadas. La humedad, absoluta y relativa, presenta un error casi dos puntos inferior al de la temperatura.

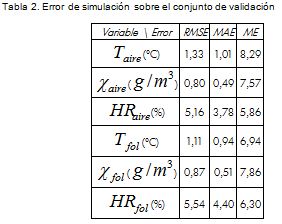
A continuación se evalúa la validez del modelo identificado, simulando el comportamiento del clima en el invernadero con los datos del conjunto de validación. Los resultados se exponen en la Tabla 2.

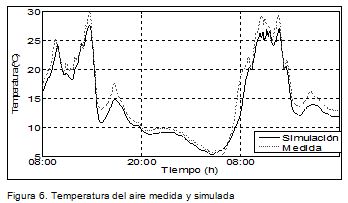
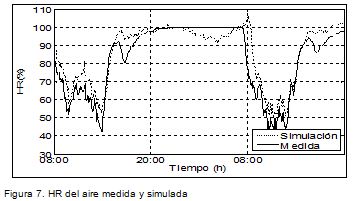
El comportamiento de la temperatura, tanto del aire como del follaje, es descrito adecuadamente por el modelo identificado. Nótese que el error RMS es de 1,33 °C, mientras que la precisión del instrumento de medida es de 0,6 °C. La Figura 6 muestra el comportamiento de la temperatura del aire en un intervalo del conjunto de validación. El modelo describe correctamente la evolución, excepto en los periodos de temperaturas altas, en los que el modelo predice temperaturas inferiores a las que realmente se presentan.

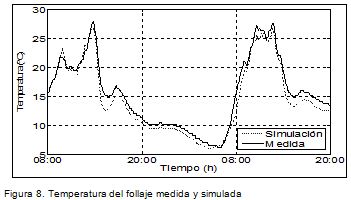
La temperatura y la humedad dentro del follaje son descritas adecuadamente por el modelo (Figura 8) para el comportamiento de la temperatura.

El modelo obtenido presenta un desempeño comparable a los resultados existentes en la literatura (ver, por ejemplo, Cunha, 2003; Herrero et al., 2003; Salgado y Cunha, 2005; Wang et al., 2000). En los trabajos citados se obtienen modelos que presentan errores RMSE alrededor de 1,5 °C para T_airey 5% X_fol. El modelo propuesto en este trabajo ofrece algunas ventajas adicionales. En primer lugar, es un sistema lineal de bajo orden; segundo, es capaz de describir adecuadamente el microclima del follaje.

Conclusiones

Se ha ofrecido el desarrollo de un modelo dinámico del clima en un invernadero ubicado en la Sabana de Bogotá. El modelo obteni-do presenta errores de simulación en los mismos órdenes de magnitud que trabajos previos, con la diferencia de que la estructura usada es lineal. Aunque no se usaron directamente en el proceso de identificación, la construcción de modelos con base en principios físicos es un paso fundamental en el proceso de identificación, ya que permite entender la estructura del sistema dinámico en estudio e interpretar los resultados obtenidos en el proceso de identificación y compararlos con el comportamiento físico de la planta.

La selección del conjunto de modelos posibles en un problema de identificación es un paso fundamental, y en este proyecto tanto la representación en variables de estados de sistemas lineales como el empleo de los algoritmos por subespacios fueron adecuados para encontrar los parámetros del sistema dinámico multivariable.

La modificación propuesta de la estructura del sistema, separando la dinámica del aire atrapado por el follaje de la del aire superior, permitió incrementar la calidad del sistema, sin sufrir un gran aumento del costo computacional. La estructura utilizada no se ha encontrado en la literatura utilizada y por tanto es un nuevo aporte que ofrece este trabajo.

Un siguiente paso en el área de agricultura de precisión es el de usar el sistema obtenido para diseñar estrategias de control basadas en modelos que optimicen la producción de cultivos bajo invernaderos.

Por otro lado, si se desea mejorar la calidad del modelo es necesario incluir más información en el proceso de identificación. En este proyecto no se midieron variables que influyen en el proceso del clima como la velocidad y dirección del viento y la temperatura del suelo y el subsuelo.

Bibliografía

Bot, G. P. A., Greenhouse climate: from physical process to a dynamical model., Ph D. thesis, Agricultural University of Wageningen, Holland, 1983.        [ Links ]

Cunha, J.B., De Moura Oliveira, J. P., Optimal management of greenhouse environments., EFITA Conference, 2003.        [ Links ]

Cunha, J. B., Greenhouse climate models: An overview., EFITA Conference, 2003.        [ Links ]

Cunha, J. B., Couto, C., Ruano, A. E., Real-time parameter estimation of dynamic temperature models for greeenhouse environmetal control., Control Engineering Practice, 1997         [ Links ]

Ghoumari, M. Y.El., Optimización de la producción de un invernadero mediante control predictivo no lineal., Ph.D. thesis, Universidad Autónoma de Barcelona, Spain, 2003.        [ Links ]

Herrero, J.M., Martínez, M., Blasco, X., Ramos, C., Rodriguez, S., Identificación paramétrica del modelo no lineal de un invernadero mediante algoritmos genéticos., XXIV Jornadas de Automática, 2003.        [ Links ]

Kania, S. Giacomelli, G., Solar radiation availability for plant growth in Arizona controlled environment agriculture systems., Proc. 30th National agricultural plastics congress, 2002.        [ Links ]

Körner, O., Crop based climate regimes for energy saving in greenhouse cultivation., PhD thesis, Agricultural University of Wageningen, Holland, 2003.        [ Links ]

Körner, O., Challa, H., Temperature integration and process based humidity control in chrysanthemum., Computers and electronics in agriculture, No. 43,2004, pp. 1–21.         [ Links ]

Overchee, V., Moor, B. L., Subspace identification for linear systems., Kluwer Academic Publishers, Dordrecht, Holland, 1996.        [ Links ]

Molina-Aiz, F., Valera, D., Alvarez, A., Measurement and simulation of climate inside Almeria-type greenhouses using computational fluid dynamics., Agricultural and Forest Meteorology, No. 125, 2004, pp. 33-51.         [ Links ]

Piñon, S., Peña, M., Alvarez, h., Kuchen, B., Control predictivo con restricciones para el clima de un invernáculo., DYNA, Revista de la Facultad de Minas de la Universidad Nacional de Colombia, No. 135, 2002, pp.11–25.        [ Links ]

Salgado, P., Cunha, J. B., Greenhouse climate hierarchical fuzzy modeling., Control Engineering Practice, No. 13, 2005,pp. 613–628.         [ Links ]

Tap, R.F., van Willigenburg, L. G., van Straten, G., Experimental results of receding horizon optimal control of greenhouse climate., Proc. Math. and Contr. Applic. in Agric. and Hort, No. 406,1996, pp. 229–238.         [ Links ]

Triguia, M., Barringtona, S., Gauthierb, L., A strategy for greenhouse climate control, part i: Model development., Journal of Agricultural Engineering Research, 2001.        [ Links ]

Wang, S., Boulard, T., Predicting the microclimate in a naturally ventilated plastic house in a Mediterranean climate., Journal of Agricultural Engineering Research, Vol. 75, No. 1, 2000,pp. 27–38.        [ Links ]

Young, P., Chotai, A., Data-based mechanistic modeling, forecasting and control., IEEE Control systems magazine, Vol. 21, No. 5, 2001, pp.14–27.        [ Links ]

Young, P. C., Lees, M. J., Chotai, A., Tych, W., Chalabi, Z. S., Modeling and PIP control of a glasshouse micro-climate., Control Engineering Practice, Vol. 2, No. 4, 1994, pp.591–604.        [ Links ]