Martin Darío Arango Serna¹, Conrado Augusto Serna² y Giovanni Pérez Ortega³

¹Industrial Engineer, Unaula. Specialist in finance, development and evaluation, Universidad de Antioquia, Medellín, Colombia. University Teaching Specialist, Universidad Politécnica de Valencia, España. M.Sc., in Computer Engineering, Universidad Nacional de Colombia. Ph.D., Industrial Engineering, Politécnica de Valencia, España. Engineering School Organization, School of Mines, Universidad Nacional de Colombia, Medellín, Colombia. mdarango@unal.edu.co

² Industrial Engineer, Universidad Nacional de Colombia. M.Sc., administrative Engineering, Universidad Nacional de Colombia, Medellín, Colombia. Instituto Tecnológico Metropolitano. casernau@unal.edu.co

³ Administrative Engineer, Universidad Nacional de Colombia. Higher education specialist, Universidad Industrial de Santander, Santander, Colombia. M.Sc., in Development, Universidad Pontificia Bolivariana. Engineering School Organization, School of Mines, Universidad Nacional de Colombia, Medellín,Colombia. gperezo@unal.edu.co

ABSTRACT

Using fuzzy set theory as a methodology for modelling and analysing decision systems is particularly interesting for researchers in industrial engineering because it allows qualitative and quantitative analysis of problems involving uncertainty and imprecision. Thus, in an effort to gain a better understanding of the use of fuzzy logic in industrial engineering, more specifically in the field of production planning, this article was aimed at providing a materials requirement planning (MRP) problem with uncertainty in the automotive industry; this was solved using fuzzy parametric linear programming.

Keywords: fuzzy mathematical programming, parametric linear programming, materials requirement planning (MRP), decision analysis.

Received: august 3th 2009

Accepted: november 15th 2010

Introduction

Decision-making is possibly one of the most important issues in which mathematics is applied in different levels of human activity; this is true if we consider that the first step for trying to solve a decision- making problem consists in formulating a mathematical model of the systems or the situation to be analysed. However, in real conditions, decision-making is imprecise, at least due to the uncertainty concerning such situation. If one wishes to create rational-suitable mathematical models of the real world, then they must be able to incorporate uncertainty and suggest how to process imprecise information (Pandian et al., 2002). It is thus possible to use the concepts and techniques of fuzzy set theory and manage imprecision in an quantitative way, since most conventional procedures do not treat imprecision and implicitly assume a fixed structure, when, in fact, decisionmaking needs flexible and robust models to deal with real life situations.For example, imprecision and uncertainty in industry are included in information about flux times, labour, materials performance, lead times, and so on. This data, which is easy to define and include in a model having absolute measurements, is always imprecise, partly due to the uncompleted information and the uncertainty that could exist with internal and external factors. It is thus attractive to solve this kind of problem through fuzzy set application.

Dan B Rinks used "if-then" linguistic rules in aggregated planning models in 1981. This technique was complemented and improved with the works of I. Burhan Turksen (Mula, 2004). Reynoso et al., (2002) presented a first draft of MRP II based on fuzzy logic and possibility theory for imprecision and uncertainty treatment of demand. Ben-Arieh et al., (2004) presented a Petri net model combining modelling, planning and evaluating performance capacity for assembly operations. This modelling tool can represent aspects related to the associated degree of difficulty in assembly sequences. Hop (2006) worked on a balancing model of a product line process using fuzzy processing times and fuzzy binary lineal programming formula for its solution. Mula (2006) developed a new lineal programming model, named MRPDet, for production planning in middle time in a materials requirement planning (MRP) manufacturing environment with capacity constraints, multi-product, multi-level and multi-period. Niu and Dartnall (2008) analysed a MRP-II-fuzzy model which included considering all the information allowing all possibilities which can occur in order-making processes. Lan et al., (2008) considered a new kind of multi-period planning problem having service levels, in which a producer has a defined number of plants and subcontracted workers for satisfying her/his product demand accordingto requested customer service level. Arango et al., (2009) have presented six fuzzy mathematical programming models applied to production planning with capacity constraints, in which uncertainty has been considered in both objective functions and constraint parameters.

Fuzzy lineal programming

The objective in a lineal programming problem in a deterministic scenario is to minimise or maximise a lineal objective function by considering lineal constrains. However, in practice, a decision-maker cannot be in a position for precisely specifying objectives or constraint functions, but it is possible to define them in imprecise terms. In such situation, it is preferred to use fuzzy lineal programming for obtaining better results in the models through the flexibility of the decision-making process (Pandian et al., 2002).

Table 1 shows a ty-pical lineal programming tool and its fuzzy equivalent.

In model (2), A‾_ij, B‾_i, C‾_j are fuzzy numbers, Xi are fuzzy variables and adding-subtracting operations are subjected to fuzzy arithmetic, Also, the "<=" symbol denotes a fuzzy unequal comparison. This model assumes that both the objective function and the constraints can include fuzzy numbers and fuzzy variables.

A fuzzy decision-making model is characterised by containing a set of possible alternatives "X" and a goal set Z_i (i = 1, 2, .., p), with constraint set B_j (j = 1, 2,., n); each of these is expressed by a fuzzy set "X". For this kind of decision-making model, Zadeh (1975), in his pioneer works, proposed that a fuzzy decision is determined by a right complement between fuzzy sets B_j (j = 1, 2,., n) and Z_i (i = 1, 2, .., p). So, fuzzy set D can be defined as: D = (Z₁ ∩ Z₂ ∩ . . . ∩ Z_p) ∩ (B₁ ∩ B₂ ∩ . . . ∩ B_n), being equal to µ_D : X → [0, 1] where µ_D(x) = mín. µ_Zi (x), µ_Bj (x), known in fuzzy set theory as a min (minimum) operator. Once fuzzy decision D is known,x^* Є X could be defined to be an optimum solution if µ_D(x^*) = máx. µ_D(x).

One consideration is to take a model with a fuzzy objective where the membership function is as follows:

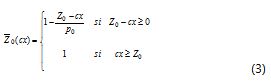
Where Z₀ is the desire level for the objective function value, and p₀ is the maximum acceptable violation of level Z₀. Likewise, constraint membership functions can be defined as:

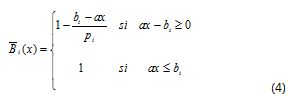
Where pi is maximum violation value of constraint i.

Chanas (1983) has argued that due to less knowledge about the fuzzy feasible region, it is not easy to establish desired level Z₀ and its tolerance to p₀; it is thus suggested first solving the model without considering the objective function to be a fuzzy one. With this approximation, the problem becomes a parametric lineal programming problem, defined as:

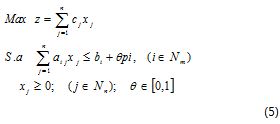
Where θ (0<=θ<=1) is a parameter interpreted as being the violation degree of the constraint, and p_i (p₁, p₂,., p_m) is the tolerance vector for each m constraint and can be defined by the decision-maker. α = 1- θ, is decision-maker satisfaction level. For each value of θ it is possible to obtain an optimum solution x*(θ) with the respective optimum value Z*(θ) where condition B‾_i(x*(θ))≥ 1-θ = α  is valid. Furthermore, for all non-null solutions, there is at least an i , so that B‾_i(x*(θ))= 1-θ . Thus, the common degree of satisfaction for the constraints is the minimum ofB‾_i(x*(θ)) , defined as B‾_c(x*(θ))=miniB‾_i(x*(θ))= 1-θ.

When solving the parametrical programming model (5) (see Hillier, 2002), a set of solutions is obtained maximising the objective function, depending on parameter θ (Safi et al., 2007). This is, for every θ, an optimal solution x*(θ) is obtained with respective Z*(θ) value that jointly satisfies constraints in degree 1- θ. This optimum solution is presented to the decision-maker who chooses Z₀ and the corresponding p₀ value. With this information it is possible to build the membership function for the objective function:

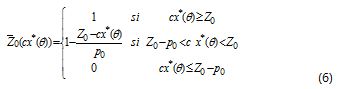
The optimal solution for this methodology is obtained by taking x*(θ*) with optimum value z*(θ*) where θ* is chosen so that μD(θ*) = maxθ μD(θ) = max θ (min (Z0(θ), Bc(θ) which is the min operator (see (Figure 1)).

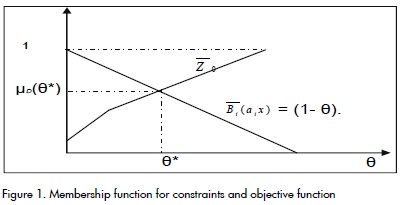
For this purpose, Jiménez et al., (2007) have used the T-rule of the algebraic product between Z0(θ) and Bc(θ) for finding the θ* value. This procedure is described in more detail in the following practical example.

MRP with uncertainty model formulation

The main objective of the production plan is to satisfy demand at lower cost. However, demand forecasting is not always accurate, thereby affecting the behaviour of the whole production system. For example, when demand is underestimated, it could generate stockouts which can lead to loss of sales, delays and definitely a bad service; on the other hand, overestimating demand can lead to having a large amount of stocks and raw materials in inventory. Companies thus use safety stocks and provide for adjustments in demand. However, the methods used for such purpose are very subjective in many cases, thus making it really important to use fuzzy models in production planning (Arango et al., 2008).

The parametric lineal programming model proposed below was aimed at minimising total costs for an MRP involving multilevel and multi-period capacity constraints. The costs considered in the models were those for delay, warehousing, ordering and capacity auditioning; it should be clarified that only marginal costs were used for this model, e.g. only costs were included that could change as a result of a particular decision made. Raw material costs were not included due to expenditure on such materials being independent of the chosen plan. Likewise, costs associated with regular work time were excluded in most situations. Moreover (at least in the short term), labour planning in terms of hiring and dismissing has little incidence on planned costs which is why such costs could be separated from the model.

In this case, uncertainty referred to constraints on inventory balance and available capacity, so that, θ (0 ≤ θ ≤ 1), represented the level at which inventory constraints and capacity were violated. Additionally to this new variable, a certain tolerance level p has been taken into account defined by p^d and p^c, representing, respectively, maximum demand and the higher percentage by which resource k would not be available. One of the model's most important set of constraints was the group of material requirement constraints, defined as follows:

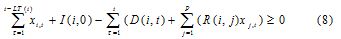
Such constrains set required that the sum of the initial inventory and production for every period was greater than or equal to the total of the sum of external demand and the demand of the sub-assemblies used in the products. Demand needed to be satisfied by the amount produced in recent or previous periods to t- LT(i) for each period, since work had to be started LT periods before it could be used to satisfy demand. Product R(i, j)*x_j,_t anticipated the demand for product i that resulted when it was a component of product j; this produc was null in almost all cases. The past constraint could also be negative for allowing delayed orders.I_i,t was thus defined as the inventory (negative or positive) of product i in period t, which was determined by:

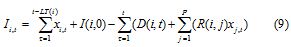
From this definition, the constraint set of the requirement balance of material and demand was re-evaluated to allow the existence of delays in orders. Instead of using equation 10, the constraint in equation 11 had to be used.

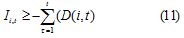
This allowed a negative inventory value. Replacing I_i,t for the expressio defining it, the constraint of material requirement and demand was reduced to:

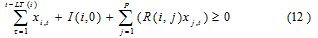
if I⁺_i,t is defined as the amount of product i in inventory and I^-_i,t the amount of product i delayed in period t, the following constrain had to be accomplished.

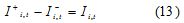
The next group in importance were the capacity constrains:

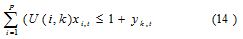
According to the right side of the equation, the capacity of resource k could be exceeded, with an associated cost and with some limitations; the extra fraction of resource k in period t was represented asy_k,t.

The next section describes an industrial process with the required information for solving the proposed MRP model to analyse the model solution through fuzzy lineal programming techniques.

Description of a selected industrial process

Vehicle assembly consists of three steps: piecing together, painting and assembly, which are sub-divided into several sub-processes and activities. Door mounting can be highlighted here as, although it is not the most complex process, it can be very representative due to its importance in final assembly. Table 2 shows the expected minimum and maximums in the 12 week study

The product explanation and subsequent analysis is only for the left door (as the right door has the same components). Table 3 shows a list of corresponding materials where S_ij represents the parent i from which part j is a component (S_4,11 then glasses - reference 11-, is a component of the glass system - reference 4) and R_ij represents the amount of products i necessary for making parent product j; delivery times (ts) are specified in weeks, initial inventory (Inv), warehousing costs (Ca) of component i by week, order costs (Cp), costs for delaying component i (Ct).

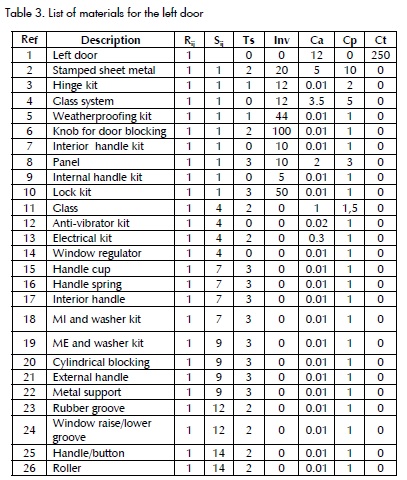
Capacity constraints only refer to the assembly line to which the selected vehicle belongs. There is 15% estimated door-mounting capacity regarding total assembly line capacity. If the company has a single labour 8 hours/week shift, there is a 40-hour weekly assembly line in which 6 hours are destined to door-mounting. The past is the actual description of company shifts. If average assembly line production capacity is 9 vehicles per hour , then door assembly time is one minute or 0.0166 hours per door.

The company can use extra labour hours for increasing available capacity. The costs involved in using every extra hour are $3,800. For practical purposes, line capacity can only be increased by 10% through extra hours. Also, pc is defined as the percentage representting assembly line non-availability. For practical purposes pc=0.01. pd is defined by the difference between maximum and minimum demand (see Table 2).

Model solution

This model can be solved in two steps.

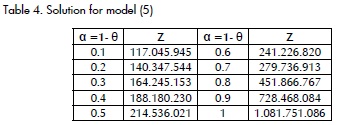
First step: model (5) is solved through parametric lineal programming and values Z₀ and P₀ are fixed. Decision-makers are thus interested in having a constraint satisfaction level set above α= 0.4, which is why Z₀=18818.023 and p₀=89.357 are defined (see Table 4).

Second step: once Z₀ and p₀ have been fixed, a membership function for the objective function is set, obtaining:

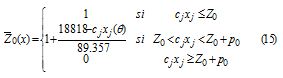
This model's graphical representation is depicted in Figure 2.

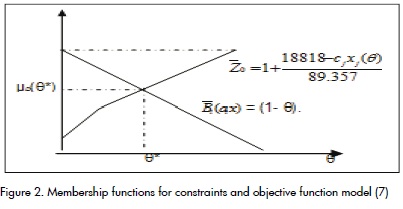
The compatibility index for each solution having the desired decision- making levels must be calculated to find an optimal solution, having a desired level satisfying both constraints and objective function membership (Jiménez et al., 2007).

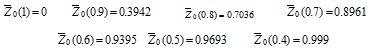
θ* must be chosen to find the correspondent optimal solution so that μ_D(θ*) = max_θ μ_D(θ) = max _θ (min (Z₀(θ), B_c(θ)). Jiménez et al., (2007) used the T-rule for the algebraic product between Z₀(θ) and B_c(θ) to find the value of θ*, as follows:

According to these results, it can be observed that θ*= 0.7 can lead to obtaining a higher satisfaction level (0.6272) regarding objective function.

Z= 28098.990; Satisfaction level = 0.6272

Result analysis

Even if the cost incurred in the solution obtained with this methodology is high regarding the desired goal, when considering capacity and demand as uncertainty values, then costs could be much higher. Plan cost Z=28098.990 is an intermediate solution balancing decision-making pessimistic and optimistic criteria, besides having a satisfaction level near to 63% regarding the lower cost that can be obtained in ideal and deterministic conditions.

Figure 3 shows the solution for μ_D(θ) and the maximum satisfaction level that can be obtained with a fuzzy solution.

It should be noticed that if a decision-maker has more accurate information, then satisfaction level will be higher. So, the usefulness of the methodology shown here is the admission of associated uncertainty levels in coefficient formulation, the goals involved in the objective function and the constraints and in the problem's resources.

Conclusions

A 0.62 satisfaction level cannot be very attractive in industrial planning; however, if considering the uncertainty factors inherent in production, this number takes on great meaning, patly due to the simplicity of its calculation and easy interpretation

The methodology presented here is just one example of the different applications for fuzzy sets and fuzzy logic for facilitating decision-making analysis related to production. These techniques should lead to practice and be validated by results obtained through conventional methods aimed at establishing the most appropriate way of making decisions in environments involving uncertainty.

A good aspect of the methodology presented here is that the complexity of an MRP model with capacity constraints is not affected by considering the uncertainty and imprecision of some of its parameters; fuzzy parametric programming can thus be an effective tool for Industrial planning.

Even if fuzzy logic is not the answer to all production system problems, this constitutes an easy-to-understand and easy-to-manage tool that can be used in most optimisation programmes. When considering membership instead of probabilistic functions, it is also more realistic regarding real production plants where uncertainty and imprecision are presented in almost all decision-making.