Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en
SciELO
Similares en
SciELO -
 Similares en Google
Similares en Google
Compartir
Ingeniería e Investigación
versión impresa ISSN 0120-5609
Ing. Investig. v.30 n.3 Bogotá sep./dic. 2010
Implementing FEM-DtN for an incompressible material on an unbounded domain
Liliana Camargo1 and Jairo Duque2
1 Mathematics, Universidad del Valle, Cali, Colombia. Universidad del Valle. lilicaz85@gmail.com.
2 Dr. rer. nat., Universidad del Valle, Cali, Colombia. jjduque@univalle.edu.co.
ABSTRACT
This paper presents the implementation of the finite element method combined with Dirichlet-to-Neumann (D†N) mapping (derived in terms of an infinite Fourier series) for studying the solvability of an exterior problem arising in linear incomepressible 2D-elasticity. A reliable numerical experiment is also presented showing the accuracy of D†N mapping; only a few Fourier series terms were needed to get a good approximation to the solution. The stable Taylor-Hood element was used for finite element discretisation.
Keywords: mixed finite element method, Taylor-Hood element, D†N technique, linear elasticity, inf-sup condition.
Received: september 4th 2009
Accepted: november 15th 2010
Introduction
This article presents a procedure for studying the Galerkin approximation to an incompressible material on unbounded exterior domain Ω. This procedure used Dirichlet-to-Neumann mapping (D†N), (Han and Bao, 1997; Gatica, Gatica and Stephan, 2003; Kako and Touda, 2004), consisting of introducing an artificial boundary by drawing circumference ΓR in R2 with radius R in domain Ω; Ω was then divided in bounded part Ωi and unbounded part ΩR. Exact and approximate boundary conditions were given on artificial boundary ΓR to solve the problem on bounded domain (Figure 1).
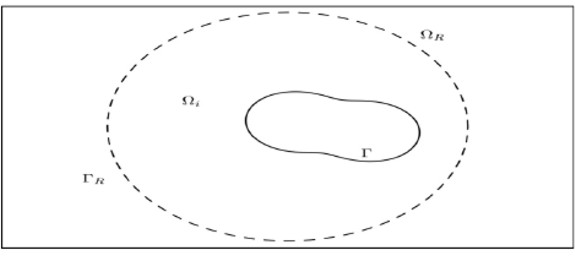
Figure 1. Domain Ω = Ωi ΩR and artificial boundary γR
Ω С R2 was an unbounded and simply connected domain with Lipschitz continuous boundary Γ. Because of Dirichlet boundary conditions on 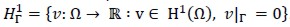 space was defined. Hence, the problem of linear elasticity consisted in finding (u,p) ∈
space was defined. Hence, the problem of linear elasticity consisted in finding (u,p) ∈ 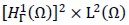 so that:
so that:
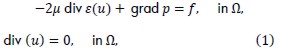
Here u: Ω → R was the displacement and ?? was the pressure of a material subjected to some external force ƒ, µ > 0 was the Lamé constant and ε(u) the strain tensor given by 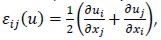 for i, j =1,2. It was assumed for this material that the stress-strain ratio was valid for small deformations, as discussed in Necas (Necas 1986; Necas, 1981; Zeidler, 1988). It was supposed that force ƒ had compact support in this work and was defined inside region Ωi.
for i, j =1,2. It was assumed for this material that the stress-strain ratio was valid for small deformations, as discussed in Necas (Necas 1986; Necas, 1981; Zeidler, 1988). It was supposed that force ƒ had compact support in this work and was defined inside region Ωi.
Next, notation 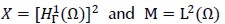 was adopted with norms L2 (Ω) and H1(Ω), respectively. Standard integration by parts led to the following variational formulation of the problem (1)
was adopted with norms L2 (Ω) and H1(Ω), respectively. Standard integration by parts led to the following variational formulation of the problem (1)
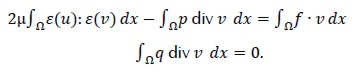
Notice that problem (1?) defined on unbounded domain Ω and Ωi was the computational domain for the finite element method used here which was obtained by introducing artificial boundary ΓR. The variational formulation of problem (1) in Ωi had to be deduced next. Integration by parts was used, by virtue of stress tensor σ (u, p):= 2 με(u) - pI, where I was the identity matrix of R2x2, this gave div (σ(u, p) = 2μ div ε (u ) + grad p, leading to weak formulation.
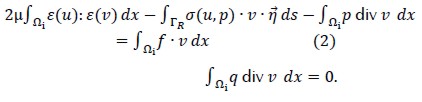
Boundary integral 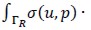
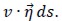 was then analyzed. The next goal was to obtain one expression representing tensor σ (u, p) on artificial boundary ΓR. The following decomposition of displacement u
on unbounded domain ΩR =
was then analyzed. The next goal was to obtain one expression representing tensor σ (u, p) on artificial boundary ΓR. The following decomposition of displacement u
on unbounded domain ΩR = 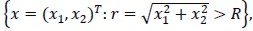
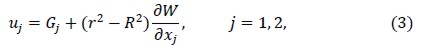
was then considered, where G1 , G2 and W were the harmonic functions to be determined. In particular, function ???? satisfied the following boundary-value problem
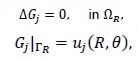
Gj is bounded, when r → + ∞.
Notice that values for Gj and ujcoincided along ΓR. Using the separation of variables method the following representations of Gj were obtained using Fourier series development
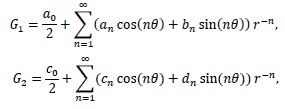
where coefficients an, bn cn and dn were given by:
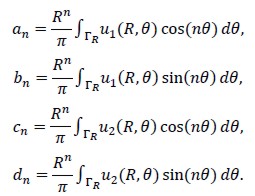
Using condition div (u)= 0 and representation (3) the following equation was obtained 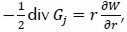 , and so .
, and so .
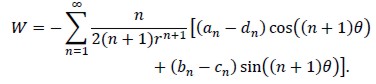
Similarly, using the balanced equation in ΩR, grad p = 2μ div ε(u) grad p = grad 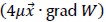 was obtained and hence
was obtained and hence 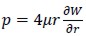 Next
Next  could be estimated along ΓR. To this end, it was first recalled that the values of uj and Gj coincided on ΓR, and pressure p was known in terms of W, leading to
could be estimated along ΓR. To this end, it was first recalled that the values of uj and Gj coincided on ΓR, and pressure p was known in terms of W, leading to
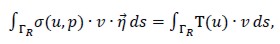
Where
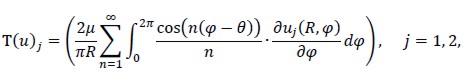
just depending on the variation of u along ΓR. Operator T(u) represented Dirichlet to Neumann mapping. It was stated that variational formulation (2) was the weak formulation of the problem
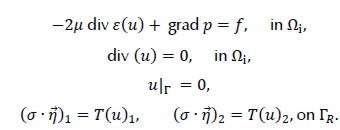
Existence and uniqueness of solutions
Bilinear forms 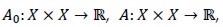
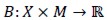 and linear functional F: X→ R defined by
and linear functional F: X→ R defined by
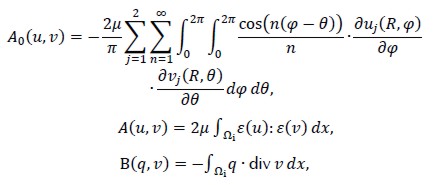
and 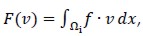 , respectively, were considered. Variational formulation of (2) would then read: Find (u,p) ∈ X x M so that
, respectively, were considered. Variational formulation of (2) would then read: Find (u,p) ∈ X x M so that
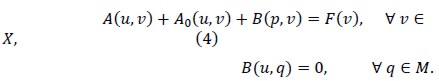
The proof of existence and uniqueness was based on Brezzi's theorem, since the form A(u,v) + A0 (u,v) was continuous andcoercive, and operator B satisfied the inf-sup condition (Han and Bao, 1997; Camargo, 2008).
Finite element method
The finite element method presented in this article did not approximate the solution of the problem (4), but provided the solution to the problem obtained by truncating operator T(u) in the corresponding Fourier series. If 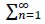 were replaced by
were replaced by  for integer value N, the variational formulation of the approximate problem would read: Find ( uN , pN ) ∈ X x M so that
for integer value N, the variational formulation of the approximate problem would read: Find ( uN , pN ) ∈ X x M so that
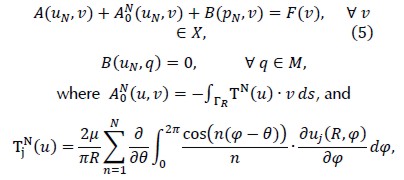
with j = 1, 2. The study of existence and uniqueness of the problem (5) was similar to the exact problem (Han and Bao, 1997; Camargo, 2008). Furthermore, the following error estimate of the approximation ( uN , pN ) held.
Theorem 1. 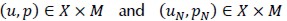 were the solutions to variational problems (4) and (5), respectively. In addition, it was supposed that
were the solutions to variational problems (4) and (5), respectively. In addition, it was supposed that 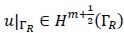 with ∈ Z. Then the following abstract error estimate would hold
with ∈ Z. Then the following abstract error estimate would hold
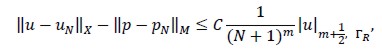
where C was a constant independent of N and M.
Next, Xh С X and Mh С M were the spaces of finite element corresponding to Taylor-Hood element (Brezzi, 1991). The regular partition of domain Ωi was denoted by Th using curved triangular elements T having diameter hT , where 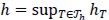 . Then, the finite element method of (5) would read: Find
. Then, the finite element method of (5) would read: Find 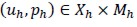 o that
o that
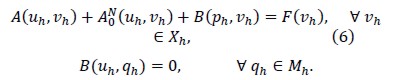
Notice that the Taylor-Hood element satisfied the inf-sup condition (Brezzi, 1991) and again, by Brezzis theorem, the unique solvability of the variational formulation (6) was obtained.
Theorem 2. 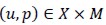 was the solution to problem (4) and
was the solution to problem (4) and 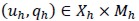 was the solution to problem (6), then the following error estimate would hold
was the solution to problem (6), then the following error estimate would hold
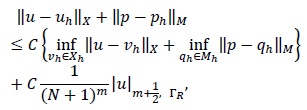
where C was a constant independent of h and N.
Proof. Let 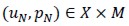 be the solution of problem (5) for any integer N ≥ 0 and consider errors
be the solution of problem (5) for any integer N ≥ 0 and consider errors 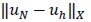 and
and 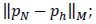 then according to the standard technique of mixed finite element method,
then according to the standard technique of mixed finite element method, 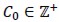 would exist independently of N and diameter h of triangulation Ωi so that
would exist independently of N and diameter h of triangulation Ωi so that
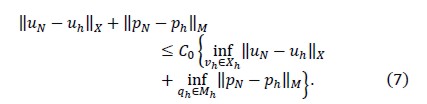
Therefore,
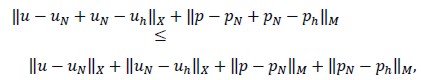
and (7) would yield
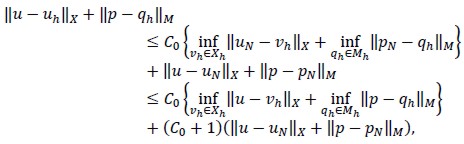
concluding the theorem proof.
Implementing the DD†N technique
Let Ω be unbounded domain 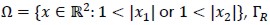 the circumference with radius R = 2 and.
the circumference with radius R = 2 and.
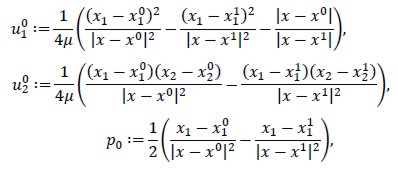
Where 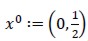 and
and 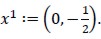 then,
then, 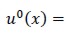
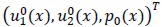 would be the unique solution for the following boundary value problem
would be the unique solution for the following boundary value problem
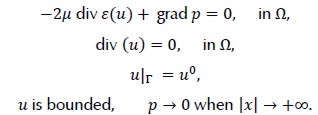
Given n ∈ N, let 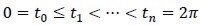 a partition uniform of
a partition uniform of 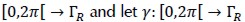 be the parametrisation of a circle defined by y(t)= R(cos (t), sen(t))T. The annular region bounded by
be the parametrisation of a circle defined by y(t)= R(cos (t), sen(t))T. The annular region bounded by 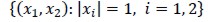 was then denoted by Ωh and closed polygonal line Γh with vertices
was then denoted by Ωh and closed polygonal line Γh with vertices 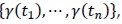 and Th was regular triangulation of Ωh with triangles T of diameter hT so that
and Th was regular triangulation of Ωh with triangles T of diameter hT so that 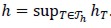 .
.
Reference triangle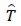 with vertices
with vertices 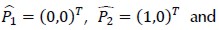
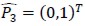 was then considered and the family of similar bijective transformations
was then considered and the family of similar bijective transformations 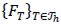 introduced so that
introduced so that 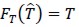 for all T ∈ Th. It is well-known that
for all T ∈ Th. It is well-known that 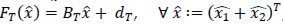 whe-re
whe-re 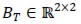 and
and  depend on the vertices of triangle T. Therefore, given integer l > 0 and subset S of R2 Pi( S) denoted the space of polynomials defined in ?? having two variables and great degrees of freedom at most L.
depend on the vertices of triangle T. Therefore, given integer l > 0 and subset S of R2 Pi( S) denoted the space of polynomials defined in ?? having two variables and great degrees of freedom at most L.
Next,
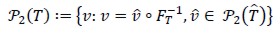
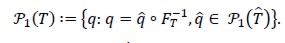
was defined to specify Xh and Mh and discretised X and M using
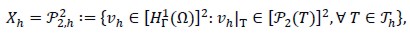
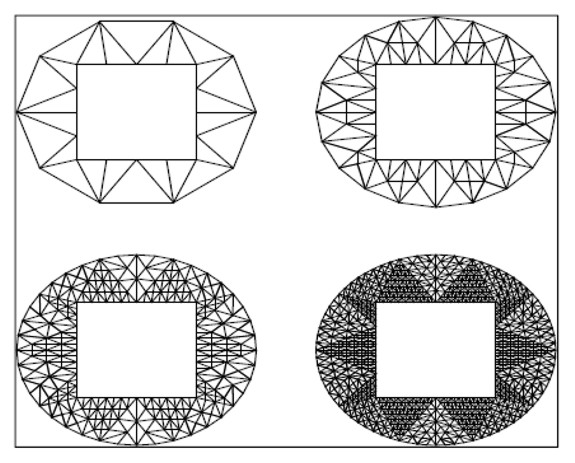
Figure 2. Sequence To,h, … T3,h of meshes used in the implementation
and
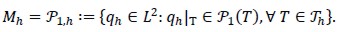
Spaces Xh and Mh were Hood and Taylor finite element subspaces satisfying inf-sup condition. Several triangulations were used in our numerical experiment. Numerical experimentation was started with initial mesh To,h which had 26 elements. Each uniformly refined mesh T1,h ,…,T3,h was generated by dividing each triangle into four smaller triagles.The result can be seean in figure 2.
Table 1. Degrees of freedom and norm L2 of errors when N = 7
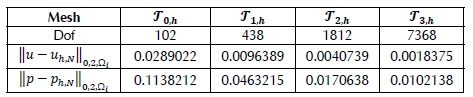
Table 1 . show norm L2 of errors u - uh,N¸ p - ph, N when N =7 for meshes To,h,…,T3,h
Table 2. Norm L2 of errors for T3,h when N = 0, 1, 3, 5, 7
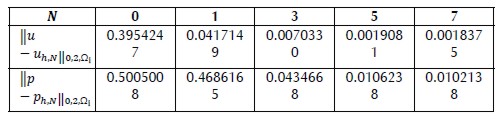
Table 2 shows norm L2 of errors u - uh,N¸ p - ph, N5 for mesh T3,h when N = 0, 1, 3, 5, 7.
Figure 3 shows values of 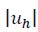 and ph for meshes T0, h, T1, h,, T3, h, and ?N = 7. As Figure 3 shows, N = 7 produced a good approximation and only a few terms were needed in bilinear form A0 to obtain good results.
and ph for meshes T0, h, T1, h,, T3, h, and ?N = 7. As Figure 3 shows, N = 7 produced a good approximation and only a few terms were needed in bilinear form A0 to obtain good results.
Conclusions
D†N mapping was used this paper to approximate the solution of an unbounded exterior problem. An artificial boundary was introduced into the domain to approximate the solution on a bounded computational domain by using a finite element method
.The Taylor-Hood element defined in terms of a Fourier series on the artificial domain was implemented in this work as finite element method. The numerical calculations showed that good convergence had been obtained just by truncating the Fourier series to seven terms. However, our discretisation produced a dense stiffness matrix, corresponding to the boundary operator; special preconditioners have to be used to obtain good convergence by very refined meshes.

Figure 3. 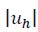 and ph for the meshes To,h,…,T1,h and T3,h when N = 7.
and ph for the meshes To,h,…,T1,h and T3,h when N = 7.
Brezzi F., Fortin M., Mixed and hybrid finite element methods.,Springer-Verlag, 1991. [ Links ]
Camargo, L., Aplicación DN-FEM a un problema elástico lineal.,BSc Mathematics thesis, Universidad del Valle, 2008. [ Links ]
Gatica G. N., Gatica L. F., Stephan E. P., A FEM–DN formulation for a non-linear exterior problem in incompressible elasticity., Mathematical Methods in the Applied sciences, 26, 2003, pp. 151–170. [ Links ]
Han H., Bao W., The artificial boundary conditions for incompressible materials on an unbounded domain.,Numerische Mathematik, 1997. [ Links ]
Kako T., Touda K., Numerical simulation of voice generation based on finite element method in unbounded region.,Department of computer science, Japan, 2004. [ Links ]
Necas, J. Introduction to the theory of nonlinear elliptic equations., John Wiley & Sons, 1986. [ Links ]
Necas, J., Hlavacek, I., Mathematical theory of elastic and elastoplastic bodies: an introduction., Elsevier scientific publishing company, 1981. [ Links ]
Zeidler, E., Nonlinear functional analysis and its applications IV., Springer-Verlag, New York, 1988. [ Links ]











 texto en
texto en 


