Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.31 no.1 Bogotá Jan./Apr. 2011
Numerical modelling of elastic behaviour of concrete reinforced with steel short fies in plane stress conditions
Fabián A. Lamus1, Manuel A. Caicedo2, Dorian L. Linero3
1 B.Sc., Civil Engineering, Universidad Industrial de Santander, Colombia .M.Sc., Structural Engineering, Universidad Nacional de Colombia. Ph.D.,student in Science and Technology of Materials, Universidad Nacional de Colombia. Auxiliar profesor, Universidad Nacional de Colombia, Bogotá falamusb@unal.edu.co
2 B.Sc., Civil Engineering. M.Sc., Structural Engineering, Universidad Nacional de Colombia, Bogota. Student Ph.D, in Structural analysis, Universidad Politécnica de Cataluña, Spain. macaicedos@unal.edu.co.
3 B.Sc. Civil Engineering. M.Sc., Structural Engineering, Universidad Nacional de Colombia. Ph.D., Structural Analysis, Universidad Politécnica de Cataluña,Colombia, Bogota. dllineros@unal.edu.co.
ABSTRACT
This work describes a numerical model of fie reinforced concrete elastic behaviour implemented using the finite elements method (Hughes, 2000). In structures made of this material, each point is formed by steel fies embedded into a simple concrete matrix. The reinforced concrete is represented inside a finite element as an orthotropic material having random material direction based on the vanishing diameter fie model (Dvorak and Bahei-el-Din, 1982) and the mixing theory modified for short length reinforcement (Oller, 2003). Statistical analysis consisted of repeating the problem's numerical simulation where the direction of fies was modified by a random function to set up a sampling database from the results and measure their variability. A sensitivity study of finite element size and the number of sampling data was then carried out in terms of total strain energy. Finite element size and sampling data are recommended. The average structural response of a reinforced concrete beam with different quantities of steel fies where minimum data dispersion was observed is given as an example of applying the above.
Keywords: Computational mechanics, mixture theory, fie reinforced concrete.
Received: June 23th 2009. Accepted: October 26th 2010
Introduction
The use of steel fie reinforced concrete (SFRC) for building structures has growth during the last few decades because of its mechanical behaviour and building advantages. Unlike plain concrete, the fies reduce the opening of micro-cracks in concrete and increase composite mechanical resistance and ductile ty. Steel reinforcement contributes towards resistance to impact, fire and aasion (ACI, 1989; ACI, 1996; ACI 1998). SFRC is currently used for building beams, columns, plates and industrial floors, likewise in arches and segments in tunnel coating.
The reinforced materials have different features compared to homogeneous materials because the fies' behaviour is modified according to their volumetric ratio and the direction in which they are orientated.
This paper presents a numerical model based on the finite elements method for simulating SFRC mechanical behaviour in the elastic range for plane stress.
Description of model for concrete reinforced with short fies
It can be supposed that SFRC in a structural element is a material consisting of steel fies with random directions embedded in a plain concrete homogenous matrix. Model formulation took the following fundamental hypotheses into account: fies are evenly distributed in the matrix, both materials' behaviour is elastic and their strains are small and adherence between matrix and fies guarantees strain compatibility and internal action transfer. The model was limited to structural elements represented by plane stress.
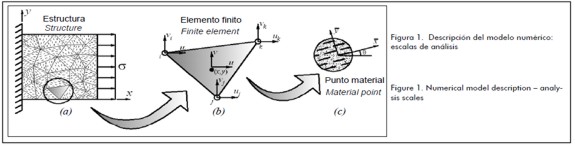
By applying the short fies mixture theory (Oller 2003) and the vanished diameter fie model (Dvorak and Bahei-el-Din, 1982) it was established that each particle of composed material had a volumetric ratio of matrix k(m) and fies k(a) with definite orientation. The latter produced composite orthotropic behaviour where the material’s major axis was parallel to the fies’ direction (as indicated in Figure 1(c)).
A parallel system formed by material components was considered in the direction parallel to fies 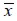 (Matthews and Rawlings,1994), where longitudinal concrete strains
(Matthews and Rawlings,1994), where longitudinal concrete strains 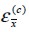 and steel
and steel 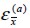 were equal to composite strain
were equal to composite strain 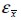 . Likewise, normal stress in composite
. Likewise, normal stress in composite 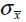 was the sum of normal stresses from component materials weighted by respective volumetric ratios, i.e.
was the sum of normal stresses from component materials weighted by respective volumetric ratios, i.e.
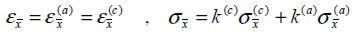 | (1) |
where steel and concrete volumetric ratios k(a) and k(c) respectively, were calculated as the volume of each component divide by the composite material’s total volume:
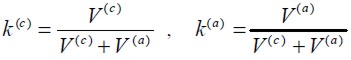 | (2) |
When material was linear elastic, the elasticity modulus for the composite material in the parallel direction to fies 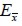 , in terms of Young modulus for concrete
, in terms of Young modulus for concrete 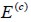 and Young modulus for steel
and Young modulus for steel 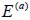 was:
was:
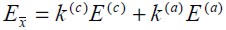 | (3) |
For reinforced material with fies where diameters were smaller than their lengths, the vanished diameter fies model could be applied. Mechanical fie contribution was thus simplified to longitudinal capacity (Dvorak and Bahei-el-Din, 1982). Consequently, the elasticity modulus perpendicular to the fie and the Poisson’s ratio of the composite material were approximately equal to the elasticity modulus and to Poisson's ratio of concrete matrix respectively, as shown below:
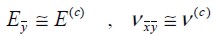 | (4) |
Equation (1) considered that normal stress in the fies was uniform along its axis; however, in materials reinforced with short fies such assessment was not entirely true. In a composed material subjected to normal stresses in the direction parallel to the fies (Figure 2 (a)), both the fie and matrix were subjected to unequal longitudinal strains around the ends of the fies (Matthews and Rawlings,1994). Consequently, the normal stress changed in the fie, as shown in Figure 2(b), and a shear stress appeared in the fie-matrix interface.
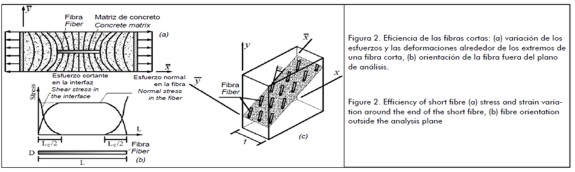
Normal stress in the fie was zero at the ends and reached maximum value at distance 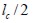 . Normal stress was kept constant from this distance to the ends of the fie. Therefore
. Normal stress was kept constant from this distance to the ends of the fie. Therefore 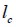 was the fie length required to keep normal stress maximum and constant. This critical length
was the fie length required to keep normal stress maximum and constant. This critical length 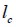 was estimated for equating shear force developed in interface
was estimated for equating shear force developed in interface 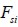 and tensile force in the fie when it reached normal failure stress
and tensile force in the fie when it reached normal failure stress 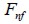 , so that:
, so that:
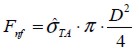 | (5) |
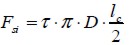 | (6) |
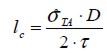 | (7) |
where 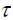 was shear stress on fie surface when subjected to failure stress
was shear stress on fie surface when subjected to failure stress 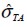 , was fie strength and
, was fie strength and 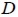 was fie diameter.
was fie diameter.
Short fie contribution to composite material stiffness was less
than continuous fie contribution due to variation in normal
stress and longitudinal strain near to its ends. This phenomenon
was represented by efficient factor 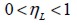 affecting the steel elasticity modulus, thus:
affecting the steel elasticity modulus, thus:
where L, D and R were fie length, diameter and spacing while 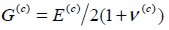 was the shear elasticity modulus of concrete.
was the shear elasticity modulus of concrete.
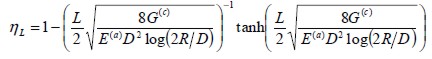 | (8) |
Simplifying the three-dimensional problem in plane stress condition limited fie orientation randomness in the analysis plane.
However, by means of another efficient factor 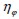 , fie orientation outside the plane could be included.
, fie orientation outside the plane could be included.
Figure 2(c) shows that the fie's longitudinal axis had random direction φ regarding material plane 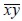 , so that composite material contribution to elasticity modulus in the analysis plane was
, so that composite material contribution to elasticity modulus in the analysis plane was 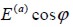 . Therefore, the efficient factor according to direction
. Therefore, the efficient factor according to direction 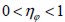 could be calculated as:
could be calculated as:
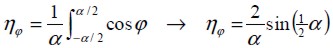 | (9) |
where a was in the value range which could be taken by direction φ.
If fie length L was less than element thickness then the fie could take a direction between 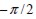 and
and 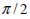 establishing angle range a equal to
establishing angle range a equal to 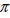 . In the opposite case, if element thickness were less than fie length, then fie orientation could only take values between -β and β and a would be equal to 2β(
. In the opposite case, if element thickness were less than fie length, then fie orientation could only take values between -β and β and a would be equal to 2β(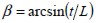 and t solid thickness).
and t solid thickness).
The elasticity modulus for reinforced material with short fies in direction 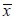 was calculated by a modification of the mixture theory, Equation (3), would thus become:
was calculated by a modification of the mixture theory, Equation (3), would thus become:
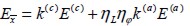 | (10) |
An orthotropic material had different mechanical properties in all three orthogonal directions of a coordinate system for material as indicated in Figure 1(c). Under plane stress, coordinate axis 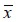 and
and 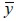 were the parallel and perpendicular directions to the fie respectively, forming angle θ regarding global coordinate axis x and y.
were the parallel and perpendicular directions to the fie respectively, forming angle θ regarding global coordinate axis x and y.
The constitutive equation for orthotropic, linear and elastic material 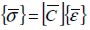 linked stress components
linked stress components 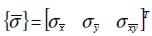 a n d s t r a i n c o m p o n e n t s
a n d s t r a i n c o m p o n e n t s 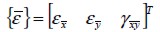 defined in material directions where
defined in material directions where 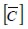 was the elastic constitutive matrix of material, in plane stress conditions corresponding to (Weaver and Johnson, 1984; Oñate and Zárate 1995)
was the elastic constitutive matrix of material, in plane stress conditions corresponding to (Weaver and Johnson, 1984; Oñate and Zárate 1995)
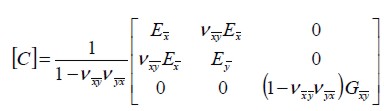 | (11) |
In the last matrix, Poisson ratio 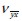 and shear elasticity modulus
and shear elasticity modulus 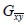 were:
were:
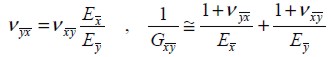 | (12) |
In the global coordinate system, the relationship between stress
components 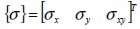 and strain components
and strain components 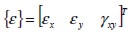 was defined as
was defined as 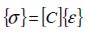 where global elastic constitutive matrix [C] was:
where global elastic constitutive matrix [C] was:
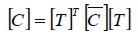 | (13) |
where [ T ] was a transformation matrix in terms of angle θ between axis 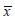 and x; thus (Weaver and Johnston, 1984):
and x; thus (Weaver and Johnston, 1984):
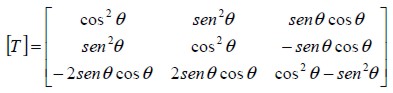 | (14) |
This paper presents a numerical model describing the elastic behaviour of reinforced concrete with short fies in random direction. The model has two analysis levels: deterministic analysis through which the structural response for each data tested was obtained and stochastic analysis establishing the dispersion of results for the set of random events.
Deterministic analysis of SFRC by finite element method
A two-dimensional model using the finite element method was implemented in the first level of analysis thereby obtaining strain energy and strain and stress distribution in a linear elastic material reinforced with short fies. Linear triangular elements were used in this model, associated with SFRC material having defined fie direction and quantities, as indicated in Figure 1(b).
For finite element e, angle 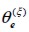 between global axis x and material axis
between global axis x and material axis 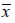 was established by a random value between
was established by a random value between 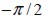 and
and 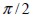 . Numerical simulation of the solid would thus have many different fie directions as the mesh has finite elements (Figure 1(a)). The actual directions of the fies in the middle was better represented by smaller finite element mesh where random fie framework was obtained in smaller sized places, as shown by some validation of the results.
. Numerical simulation of the solid would thus have many different fie directions as the mesh has finite elements (Figure 1(a)). The actual directions of the fies in the middle was better represented by smaller finite element mesh where random fie framework was obtained in smaller sized places, as shown by some validation of the results.
Stochastic analysis of random fie orientation in SFRC
Stochastic mechanics analyses random variable dispersion obtained from deterministic mechanical laws in each event or test data (Ostoja-Starzewski, 2008).
Each event 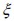 corresponded to a deterministic analysis of the problem where a random value for fie direction
corresponded to a deterministic analysis of the problem where a random value for fie direction 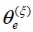 had been chosen for each finite element. The results arising from such event were indicated by
had been chosen for each finite element. The results arising from such event were indicated by 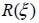 .
.
Stochastic analysis repeated the deterministic problem forming a set of events in test space size m and studied results dispersion, defined as:
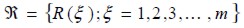 | (15) |
Each time a deterministic problem was solved a different solution was obtained. For example, the strain energy of a specimen subjected to uniform pressure would be different in each event; however, every value for energy would be greater than the strain energy given when fies had a perpendicular direction to load and this was less than the strain energy when fies were parallel to it.
It would be expected that results' dispersion would decrease when testing space m and finite element mesh density increased for the SFRC model. Consequently, the orthotropic behaviour of random material direction for SFRC at each material point would become isotropic in structural element volume. The model was implemented in PEFiCA finite element openâcode software (Linero,2009).
Elasticity modulus equal to isotropic material
As a validation example for the model, a square panel having side L and SFRC thickness t was analysed. This panel was submitted to a distributed load per unit of area q applied to one of its sides, as shown in Figure 3(a).
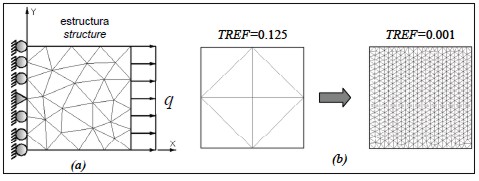
Figure 3. Uniform pressure panel: (a) general scheme, (b) finite elemen meshes
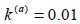 volumetric ratio for steel was used, representing habitual steel fie content in structural concrete matrix. The ratio between elasticity modulus in material directions
volumetric ratio for steel was used, representing habitual steel fie content in structural concrete matrix. The ratio between elasticity modulus in material directions 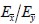 was about 1.05.
was about 1.05.
The energy strain of a solid in event  was the result of addingthe strain energies for each finite element mesh, calculated as:
was the result of addingthe strain energies for each finite element mesh, calculated as:
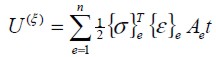 | (16) |
where n was the number of finite elements and 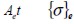 , and
, and 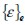 were finite element volume, stress vector and strain vector, respectively.
were finite element volume, stress vector and strain vector, respectively.
The analytical form of strain energy for an isotropic and elastic
panel having dimensions 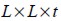 , subjected to pressure q, was:
, subjected to pressure q, was:
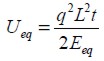 | (17) |
where 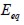 , was the equivalent elasticity modulus for isotropic material.
, was the equivalent elasticity modulus for isotropic material.
Equalizing the strain energy calculated in event 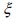 from equation (16) with equivalent energy of an isotropic model indicated in equation (17), the elasticity modulus equivalent to isotropic material in event
from equation (16) with equivalent energy of an isotropic model indicated in equation (17), the elasticity modulus equivalent to isotropic material in event 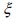 could be expressed as:
could be expressed as:
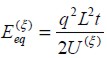 | (18) |
Average value 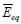 and standard deviation
and standard deviation 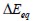 for the equivalent elasticity modulus in the whole events was:
for the equivalent elasticity modulus in the whole events was:
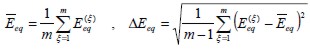 | (19) |
The problem was simulated using 5 meshes having different density and testing fields m until 250 events to obtain modulus 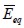 and its dispersion. The relative size of finite element TREF was defined as the ratio between finite element area
and its dispersion. The relative size of finite element TREF was defined as the ratio between finite element area 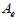 and modelled structure area
and modelled structure area 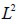 , so meshes had maximum density
, so meshes had maximum density 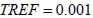 and minimum density
and minimum density 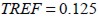 ,as shown in Figure3 (b).
,as shown in Figure3 (b).
The average and standard deviation for the equivalent elasticity
modulus of the composite material divided by Young modulus
for concrete 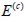 is indicated in Figure 4.
is indicated in Figure 4.
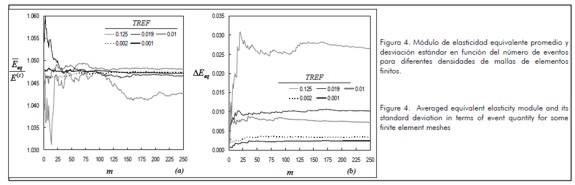
This Figure shows that dispersion decreased when test field size was increased. For example, if 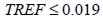 and test size was 30 events, then the standard deviation for the equivalent elastic modulus was less than 1.0%. Likewise, mesh density reduced result dispersion as indicated by 3.0% standard deviation for lower density mesh and 0.2% in the refined mesh.
and test size was 30 events, then the standard deviation for the equivalent elastic modulus was less than 1.0%. Likewise, mesh density reduced result dispersion as indicated by 3.0% standard deviation for lower density mesh and 0.2% in the refined mesh.
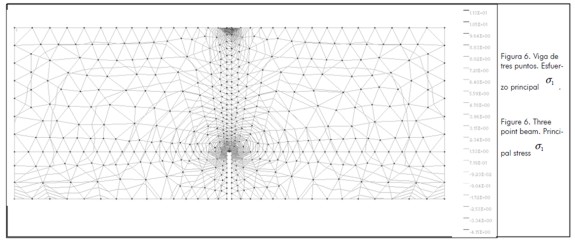
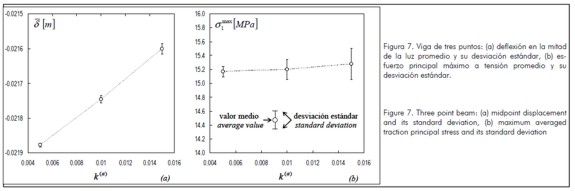
Application example: three point beam
The elastic behaviour of an SFRC beam with a notch in the middle of the span was simulated; this was subjected to point load 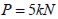 , as indicated in Figure 5 (Ferrara and Gettu, 2000). The beam was
, as indicated in Figure 5 (Ferrara and Gettu, 2000). The beam was 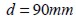 high,
high, 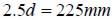 long and thick. The notch was 2.5mm wide and 23.13mm deep.
long and thick. The notch was 2.5mm wide and 23.13mm deep.
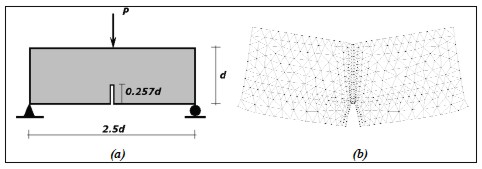
Figure 5. Three point beam: (a) overall scheme, (b) deformed shape of finite element mesh
The mechanical characteristics of the plain concrete matrix were as follows: Young’s modulus 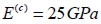 , Poisson ratio
, Poisson ratio 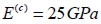 and compression resistance
and compression resistance 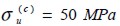 . By comparison, the short steel fies had Young’s modulus
. By comparison, the short steel fies had Young’s modulus 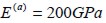 , Poisson ratio
, Poisson ratio 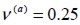 and yielding stress
and yielding stress 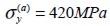 , likewise its volumetric participation coefficient
k(a) was 0.01, its length l was 60 mm and its diameter D was 2mm.
, likewise its volumetric participation coefficient
k(a) was 0.01, its length l was 60 mm and its diameter D was 2mm.
Applying equation (9) to 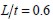 , an efficient factor for fie plane direction
, an efficient factor for fie plane direction 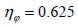 was obtained.
was obtained.
Each fie’s cross section area was 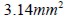 ; then, for volume ratio
; then, for volume ratio 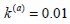 , total transversal section area was
, total transversal section area was 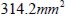 and concrete matrix cross section area was
and concrete matrix cross section area was 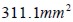 . If the whole cross section were assumed to be square, then minimum spacing between two neighbouring parallel fies R would be equal to the square side, i.e.
. If the whole cross section were assumed to be square, then minimum spacing between two neighbouring parallel fies R would be equal to the square side, i.e. 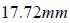 . When
. When 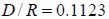 and
and 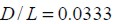 ratios were obtained, the efficient factor for stress variations at fie extremes
ratios were obtained, the efficient factor for stress variations at fie extremes 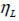 was 0.8176.
was 0.8176.
The panel was divided into 883 linear triangular elements, corresponding to factor TREF= 0,00113 and 25 events were carried out with fie random orientation. Figure 5(b) and Figure 6 illustrate the deformed shape and main stresses  for the beam for one of the events.
for the beam for one of the events.
The chosen number of test data followed down standard deviation shown in the uniaxial test for relative finite element size TREF between 0.001 and 0.002, as indicated in Figure 4.
An average deflection value 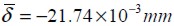 having 0.05% standard deviation and
having 0.05% standard deviation and 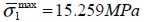 averege stress value, with 0.85% standard deviation were obtained from stochastic analysis of deflection results in the middle of span δ and maximum main tensile stress
averege stress value, with 0.85% standard deviation were obtained from stochastic analysis of deflection results in the middle of span δ and maximum main tensile stress 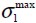 .
.
Deflections and average stresses having very small dispersions were obtained when analysing the three point beam with 0.005 and 0.015 volumetric ratios, as indicated in Figure 7.
Conclusions
The model presented in this paper represented SFRC structural elements’ elastic behaviour by means of two levels of analysis: deterministic, where each finite element was associated with a composite material having random material orientation and stochastic analysis where deterministic analysis event results were collected and their dispersion compared to average values was studied.
SFRC elastic behaviour was obtained from component materials’ four properties: Young's modulus and Poisson ratio for plain concrete matrix and Young's modulus and volumetric ratio for steel fies.
The model showed that orthotropic behaviour for random material direction at each point of the body could be represented as approximated isotropic behaviour for the structural element.
Test field size determined response dispersion in stochastic analysis. Standard deviation was reduced when computing average equivalent elasticity module test date size was increased; however, such reduction had an asymptote determined by mesh density. A lower density test field would be needed for the thinner mesh to obtain lower constant standard deviations.
Experimental testing of structural elements can be simulated with this model to determine displacement, strain and average stress with their respective standard deviations. The behaviour of a notched beam having a point load in the middle was simulated to show such application with three reinforcement fie ratios, obtaining standard deviations for deflection of less than 0.1%.
Acknowledgements
The authors are grateful to the Universidad Nacional de Colombia’s Research Division, Bogotá, for financial support provided by Project DIB-7006.
Nomenclature
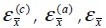 Concrete, steel and composite materia longitudinal strain in direction to the fiber.
Concrete, steel and composite materia longitudinal strain in direction to the fiber.
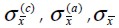 Concrete, steel and composed material
normal stress in direction to the fiber.
Concrete, steel and composed material
normal stress in direction to the fiber.
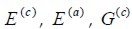 Young’s modulus of concrete, steel and shear elasticity modulus of concrete.
Young’s modulus of concrete, steel and shear elasticity modulus of concrete.
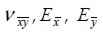 Poisson’s ratio, parallel and perpendicular to the composite material fiber elasticity modulus
Poisson’s ratio, parallel and perpendicular to the composite material fiber elasticity modulus
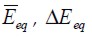 Average value and standard deviatio module of equivalent elasticity modulus for whole made events.
Average value and standard deviatio module of equivalent elasticity modulus for whole made events.
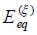 Equivalent elasticity modulus for an isotropic material in the event
Equivalent elasticity modulus for an isotropic material in the event 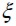 .
.
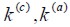 Volumetric ratios of the concrete matrix and the steel fibers.
Volumetric ratios of the concrete matrix and the steel fibers.
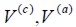 Concrete and Steel fibers volume contained into the referenced volume of composite material.
Concrete and Steel fibers volume contained into the referenced volume of composite material.
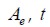 Area and thickness of a finite element.
Area and thickness of a finite element.
L, D, R,Length, diameter and average spacing of the short fiber.
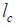 Transition length of the short fiber.
Transition length of the short fiber.
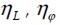 Efficient factor for the short fiber behavior and efficient factor for the fibers orientation probability out the concrete panel plane.
Efficient factor for the short fiber behavior and efficient factor for the fibers orientation probability out the concrete panel plane.
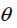 Fiber orientation angle in the plane xy between axis x and
Fiber orientation angle in the plane xy between axis x and 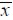 .
.
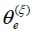 Angle of fiber orientation into the plane for the finite element (e) in the event
Angle of fiber orientation into the plane for the finite element (e) in the event 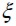 .
.
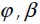 Angle of fiber orientation out the plane xy in the solid and maximum angle of fiber orientation out the plane xy if itself thickness is less than the fiber total length.
Angle of fiber orientation out the plane xy in the solid and maximum angle of fiber orientation out the plane xy if itself thickness is less than the fiber total length.
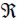 Testing results field obtained in the analysis.
Testing results field obtained in the analysis.
m Number of events 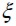 for the results field.
for the results field.
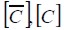 Constitutive elastic matrix in material coordinates and in global coordinates respectively.
Constitutive elastic matrix in material coordinates and in global coordinates respectively.
[ T ] Transformation matrix in terms of angle θ .
q Applied load per unit of area over one of the solid sides.
TREF Relative size of the finite element.
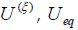 Solid strain energy for an event
Solid strain energy for an event 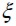 and equivalent energy analytically calculated for an isotropic elastic solid
and equivalent energy analytically calculated for an isotropic elastic solid
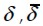 Deflection and average deflection in the middle of the span.
Deflection and average deflection in the middle of the span.
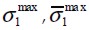 Maximum principal tensile stress for
composite and its average value respectively
Maximum principal tensile stress for
composite and its average value respectively
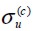 Compression resistance of the concrete used in the beam test.
Compression resistance of the concrete used in the beam test.
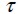 Shear stress acting over the fiber surface when it is subjected to the failure stress.
Shear stress acting over the fiber surface when it is subjected to the failure stress.
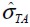 Tensile strength of the fiber.
Tensile strength of the fiber.
References
ACI, Technical Report ACI 544.2R., Measurement of Properties of Fiber Reinforced Concrete., United States of America, 1989. [ Links ]
ACI, Technical Report ACI 544.1R., State of the Art Report on Fiber Reinforced Concrete., United States of America, 1996. [ Links ]
ACI, Technical Report ACI 506.1R., Committee Report on Fiber Reinforced Shotcrete., United States of America, 1998. [ Links ]
Dvorak, G., Bahei-el-Din, Y., Plasticity analysis of fibrous composites., Journal of Applied Mechanics, Vol. 49, 1982, pp. 327-335. [ Links ]
Ferrara, L., Gettu, R., Non-local damage analysis of three-point bending tests on SFRC notched beams., Fifth RILEM symposium on fibre-reinforced concrete (FRC), 2000, pp. 357-367. [ Links ]
Hughes, T. J. R., The finite element method., New York, Dover, 2000. [ Links ]
Linero, D., PEFiCA - Programa de elementos finitos a código abierto. versión 1.0., Bogotá, Universidad Nacional de Colombia, 2010. [ Links ]
Matthews, F. L., Rawlings, R. D., Composite materials: engineering and Science., Cambridge, Woodhead Publishing Limited, 1994. [ Links ]
Oller, S., Simulación numérica del comportamiento mecánico de los materiales compuestos., Barcelona, CIMNE, 2003. [ Links ]
Oñate, E., Structural Analysis with the Finite Element Method., CIMNE - Springer, 2009. [ Links ]
Oñate, E., Zárate, F., Cálculo de estructuras por el método de los elementos finitos., Barcelona, Centro Internacional de Métodos Numéricos en Ingeniería, 1995. [ Links ]
Ostoja-Starzewski, M., Microestructural randomness and scaling in mechanics of materials., Boca Raton, USA, Chapman & Hall/CRC, 2008. [ Links ]
Weaver, J., Johnson, C., Finite elements for structural analysis., New Jersey, Prentice Hall, 1984. [ Links ]











 text in
text in 


