Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.31 no.1 Bogotá Jan./Apr. 2011
Simulación numérica del comportamiento elástico del concreto reforzado con fibras cortas de acero en condición plana de esfuerzos
Numerical modelling of elastic behaviour of concrete reinforced with steel short fibres in plane stress conditions
Fabián A. Lamus1, Manuel A. Caicedo2, Dorian L. Linero3
1 B.Sc., Ingeniería Civil de la Universidad Industrial de Santander, M.Sc. en Estructuras de la Universidad Nacional de Colombia. Estudiante del Doctorado en Ingeniería - Ciencia y Tecnología de materiales, Universidad Nacional de Colombia. Docente auxiliar, Universidad Nacional de Colombia, Bogotá. falamusb@unal.edu.co.
2 B.Sc. Ingeniería Civil y M.Sc. en Estructuras, Universidad Nacional de Colombia. Estudiante del Doctorado en Análisis Estructural, Universidad Politécnica de Cataluña, España. macaicedos@unal.edu.co.
3 B.Sc., Ingeniero Civil y M.Sc. en Estructuras, Universidad Nacional de Colombia. Ph.D. en Análisis Estructural, Universidad Politécnica de Cataluña, España. Profesor Asistente, Facultad de Ingeniería, Universidad Nacional de Colombia, Bogotá. dllineros@unal.edu.co.
RESUMEN
Este trabajo describe un modelo numérico implementado en el método de los elementos finitos (Hughes, 2000), el cual permite simular el comportamiento elástico del concreto reforzado con fibras cortas de dirección aleatoria. En estructuras hechas de dicho material cada punto está compuesto por fibras cortas de acero embebidas en una matriz de concreto simple. En el interior de un elemento finito el concreto reforzado se representa como un material ortótropo de dirección material aleatoria, basado en el modelo de fibras con diámetro despreciable (Dvorak y Bahei-el-Din, 1982) y la teoría de mezclas modificada para refuerzo de corta longitud (Oller, 2003). El análisis estadístico realizado consiste en: repetir la simulación numérica del problema cambiando la dirección de las fibras mediante una función aleatoria, construir la base de datos de muestreo a partir de los resultados obtenidos y medir la dispersión de estos últimos. A continuación, en este trabajo se estudia la sensibilidad del tamaño de los elementos finitos y del número de datos de muestreo en el cálculo de la energía total de deformación y se establecen algunos valores recomendables. Como ejemplo de aplicación se obtuvo la respuesta estructural promedio de una viga de concreto reforzado con diferentes cuantías de fibras cortas de acero, observando una dispersión mínima de los datos.
Palabras claves: mecánica computacional, teoría de mezclas, concreto reforzado con fibras.
Recibido: junio 23 de 2009. Aceptado: octubre 26 de 2010
Introducción
En las últimas décadas la utilización del concreto reforzado con fibras cortas de acero (CRFC) en la construcción de obras civiles ha aumentado notoriamente debido a su comportamiento mecánico y a sus ventajas constructivas. A diferencia del concreto simple, la presencia de las fibras reduce la abertura de las microfisuras en el concreto y aumenta la resistencia mecánica y la ductilidad del compuesto. Asimismo, el acero de refuerzo contribuye a la resistencia al impacto, al fuego y a la abrasión (ACI, 1989; ACI, 1996; ACI, 1998). En la actualidad el uso del CRFC se extiende a la construcción de vigas, columnas, placas de entrepiso y pisos industriales en edificaciones, como también arcos y dovelas en el revestimiento de túneles, entre otros.
Los materiales reforzados presentan características diferentes con respecto a los materiales homogéneos debido a que las fibras modifican su comportamiento dependiendo de su participación volumétrica y del sentido en que se encuentren orientadas.
En este trabajo se desarrolla un modelo numérico implementado en el método de los elementos finitos para simular el comportamiento mecánico del CRFC en el rango elástico, en un estado plano de esfuerzos.
Descripción del modelo de concreto reforzado con fibras cortas
En un elemento estructural se puede suponer que el concreto reforzado con fibras cortas es un material compuesto que está constituido por fibras de acero de orientación aleatoria embebidas en una matriz homogénea de concreto simple. En la formulación del modelo se tienen las siguientes hipótesis fundamentales: 1) las fibras se distribuyen uniformemente en la matriz, 2) el comportamiento de ambos materiales es elástico y sus deformaciones son pequeñas, y 3) la adherencia entre la matriz y las fibras asegura la compatibilidad de deformaciones y la transferencia de acciones internas. Asimismo, el modelo está limitado a elementos estructurales representados mediante un estado plano de esfuerzos.
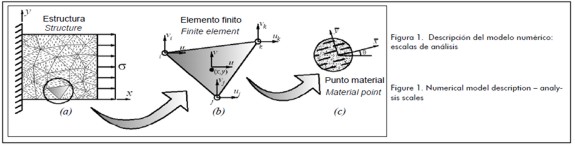
Con la aplicación de la teoría de mezclas para fibras cortas (Oller, 2003) y el modelo de fibras con diámetro despreciable (Dvorak y Bahei-el-Din, 1982) se establece que cada partícula de material compuesto contiene una fracción de participación volumétrica de la matriz y k(m) de las fibras k(a) con orientación definida. Lo anterior produce un comportamiento ortótropo del compuesto, cuyo eje material mayor es paralelo a la dirección de las fibras, como se indica en la Figura 1(c).
En la dirección paralela a las fibras 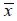 se considera que los materiales componentes constituyen un sistema en paralelo (Matthews y Rawlings, 1994), en el cual las deformaciones longitudinales del concreto
se considera que los materiales componentes constituyen un sistema en paralelo (Matthews y Rawlings, 1994), en el cual las deformaciones longitudinales del concreto 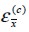 y del acero
y del acero 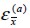 son iguales a la deformación del compuesto
son iguales a la deformación del compuesto 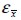 . Asimismo, el esfuerzo normal del compuesto
. Asimismo, el esfuerzo normal del compuesto 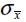 corresponde a la suma de los esfuerzos normales de los materiales componentes
corresponde a la suma de los esfuerzos normales de los materiales componentes 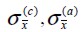 ponderada por los coeficientes de participación volumétrica correspondientes, es decir:
ponderada por los coeficientes de participación volumétrica correspondientes, es decir:
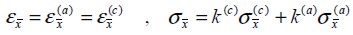 | (1) |
Donde los coeficientes de participación volumétrica del acero y del concreto, k(a) y k(c) respectivamente, se calculan como los cocientes entre el volumen de cada uno de los componentes y el volumen total del material compuesto:
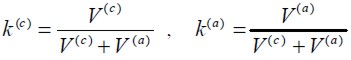 | (2) |
Si el material es lineal elástico el módulo de elasticidad para el material compuesto en la dirección paralela a las fibras 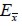 , en términos del módulo de Young del concreto
, en términos del módulo de Young del concreto 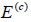 y del acero
y del acero 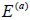 es igual a:
es igual a:
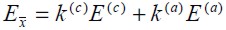 | (3) |
Para materiales reforzados con fibras de diámetro mucho menor que su longitud se puede aplicar el modelo de la fibra con diámetro despreciable, el cual simplifica el aporte mecánico de la fibra a su capacidad axial (Dvorak y Bahei-el-Din, 1982). En consecuencia, el módulo de elasticidad perpendicular a la fibra y la relación de Poisson del material compuesto son aproximadamente iguales al módulo de elasticidad y a la relación de Poisson de la matriz de concreto respectivamente, como se indica a continuación:
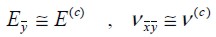 | (4) |
La ecuación (1) considera que el esfuerzo normal en las fibras es uniforme a lo largo de su eje; sin embargo, en materiales reforzados con fibras cortas esta apreciación no es completamente válida. En un material compuesto solicitado a esfuerzos normales paralelos a la fibra (figura 2 (a)), la matriz y la fibra experimentan deformaciones longitudinales diferentes alrededor de los extremos de la fibra (Matthews y Rawlings, 1994). En consecuencia, el esfuerzo normal de la fibra varía, como se muestra en la Figura 2 (b), y aparece un esfuerzo cortante en la interfaz fibramatriz.
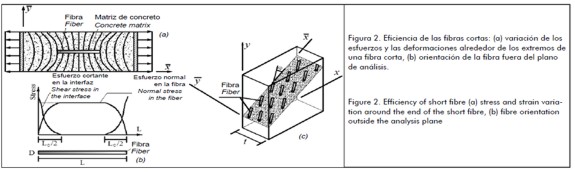
El esfuerzo normal en la fibra es cero en sus extremos y aumenta hasta un valor máximo a una distancia 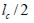 . A partir de esta distancia a los extremos de la fibra el esfuerzo normal se conserva constante. Por lo tanto
. A partir de esta distancia a los extremos de la fibra el esfuerzo normal se conserva constante. Por lo tanto 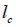 corresponde a la longitud de la fibra necesaria para que el esfuerzo normal adquiera un valor máximo constante. Ésta longitud crítica
corresponde a la longitud de la fibra necesaria para que el esfuerzo normal adquiera un valor máximo constante. Ésta longitud crítica 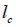 se determina igualando la fuerza cortante desarrollada en la interfaz
se determina igualando la fuerza cortante desarrollada en la interfaz 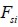 y la fuerza de tensión en la fibra cuando ésta alcanza el esfuerzo de falla
y la fuerza de tensión en la fibra cuando ésta alcanza el esfuerzo de falla 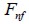 , de la forma:
, de la forma:
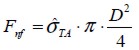 | (5) |
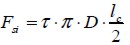 | (6) |
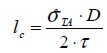 | (7) |
donde 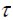 es el cortante actuante sobre la superficie de la fibra cuando ésta se encuentra sometida a la tensión de falla,
es el cortante actuante sobre la superficie de la fibra cuando ésta se encuentra sometida a la tensión de falla, 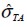 es la resistencia de la fibra y
es la resistencia de la fibra y 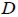 es su diámetro.
es su diámetro.
Debido a la variación del esfuerzo normal y la deformación longitudinal cerca de sus extremos, la fibra corta aporta menos a la rigidez del compuesto que la fibra continua. Este fenómeno se representa mediante un factor de eficiencia 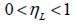 que multiplica al módulo de elasticidad del acero de la forma:
que multiplica al módulo de elasticidad del acero de la forma:
donde L, D y R corresponden a la longitud, el diámetro y la
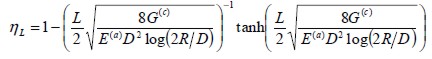 | (8) |
separación de las fibras, mientras que 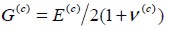
es el módulo de elasticidad a cortante del concreto.
Por otra parte, la simplificación del problema tridimensional a una condición plana de esfuerzos limita el carácter aleatorio de la orientación de las fibras al plano de análisis. Sin embargo, mediante otro factor de eficiencia 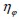 se puede incluir la orientación de la fibra fuera del plano.
se puede incluir la orientación de la fibra fuera del plano.
Como se indica en la figura 2(c), el eje longitudinal de la fibra tiene una orientación aleatoria φ respecto al plano material 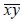 , de manera que el aporte de su módulo de elasticidad al material compuesto en el plano de análisis es igual a
, de manera que el aporte de su módulo de elasticidad al material compuesto en el plano de análisis es igual a 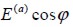 . Por lo tanto, el factor de eficiencia debido a la orientación
. Por lo tanto, el factor de eficiencia debido a la orientación 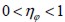 puede calcularse como:
puede calcularse como:
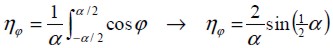 | (9) |
donde a está en el rango de valores que puede tomar la orientación φ .
Si la longitud de la fibra, L, es menor que el espesor del elemento, la fibra podrá tomar una orientación entre 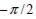 y
y 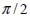 determinando así un rango de ángulos a igual a
determinando así un rango de ángulos a igual a 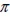 . En caso contrario, si el espesor del elemento es menor que la longitud de la fibra, la orientación de esta última podrá tomar valores sólo entre -β y β y a será igual a 2β, siendo
. En caso contrario, si el espesor del elemento es menor que la longitud de la fibra, la orientación de esta última podrá tomar valores sólo entre -β y β y a será igual a 2β, siendo 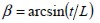 y t el espesor del sólido.
y t el espesor del sólido.
El módulo de elasticidad del material reforzado con fibras cortas en la dirección 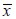 se obtiene como una modificación de la ecuación (3) de la teoría de mezclas, así:
se obtiene como una modificación de la ecuación (3) de la teoría de mezclas, así:
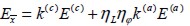 | (10) |
Un material ortótropo cuenta con propiedades mecánicas diferentes en las tres direcciones ortogonales entre sí que conforman un sistema coordenado propio del material, como se indica la figura 1(c). En condición plana de esfuerzos los ejes coordenados 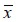 y
y 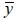 corresponden a la dirección paralela y perpendicular a la fibra respectivamente, las cuales forman un ángulo θ con respecto a los ejes coordenados globales x y y.
corresponden a la dirección paralela y perpendicular a la fibra respectivamente, las cuales forman un ángulo θ con respecto a los ejes coordenados globales x y y.
La ecuación constitutiva de un material lineal elástico ortótropo 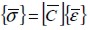 relaciona las componentes del esfuerzo
relaciona las componentes del esfuerzo 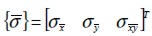 y de deformación
y de deformación 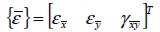 definidas en las direcciones materiales, siendo
definidas en las direcciones materiales, siendo 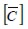 la matriz constitutiva elástica material, que en condición plana de esfuerzos (Weaver y Johnson, 1984; Oñate y Zárate, 1995; Oñate, 2009) corresponde a:
la matriz constitutiva elástica material, que en condición plana de esfuerzos (Weaver y Johnson, 1984; Oñate y Zárate, 1995; Oñate, 2009) corresponde a:
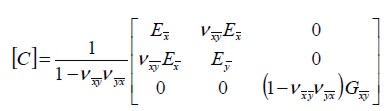 | (11) |
En la matriz anterior la relación de Poisson 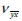 y el módulo de elasticidad a cortante
y el módulo de elasticidad a cortante 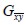 son iguales a:
son iguales a:
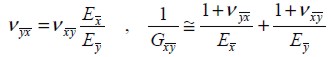 | (12) |
En el sistema coordenado global la relación entre las componentes de esfuerzo 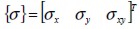 y de deformación
y de deformación 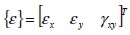 , se define como
, se define como 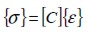 , donde la matriz constitutiva elástica global es [C] igual a:
, donde la matriz constitutiva elástica global es [C] igual a:
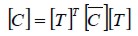 | (13) |
donde [ T ] es una matriz de transformación en términos del ángulo θ formado entre los ejes 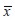 y x (Weaver y Johnson, 1984) de la forma:
y x (Weaver y Johnson, 1984) de la forma:
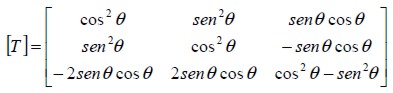 | (14) |
Este trabajo presenta un modelo numérico que describe el comportamiento elástico del concreto reforzado con fibras cortas de orientación aleatoria. Tal modelo incluye dos niveles de análisis: el análisis determinista, mediante el cual se obtiene la respuesta estructural para cada dato de muestreo, y el análisis estocástico, que establece la dispersión de los resultados del conjunto de eventos aleatorios pertenecientes al espacio de muestreo.
Análisis determinista del CRFC por medio del método de los elementos finitos
En el primer nivel de análisis se implementó un modelo bidimensional en el método de los elementos finitos, el cual permite obtener la energía de deformación y la distribución de deformaciones y esfuerzos en un material reforzado elástico lineal con fibras cortas. En este modelo se utilizó un elemento triangular lineal asociado a un solo material reforzado con fibras cortas de dirección y cantidad definida, como lo indica la figura 1(b).
Para un elemento finito e, el ángulo 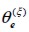 conformado entre el eje global x y el eje material
conformado entre el eje global x y el eje material 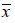 se establece con el valor aleatorio entre
se establece con el valor aleatorio entre 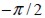 y
y 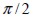 , de ahí que la simulación numérica del sólido tendrá tantas direcciones de fibra diferentes como elementos finitos tenga la malla (figura1(a)). La dirección real de las fibras en el medio se representará mejor con mallas de elementos finitos más pequeños, donde el carácter aleatorio de la fibra se obtenga en regiones de menor tamaño, como se demostrará más adelante en algunos resultados de validación.
, de ahí que la simulación numérica del sólido tendrá tantas direcciones de fibra diferentes como elementos finitos tenga la malla (figura1(a)). La dirección real de las fibras en el medio se representará mejor con mallas de elementos finitos más pequeños, donde el carácter aleatorio de la fibra se obtenga en regiones de menor tamaño, como se demostrará más adelante en algunos resultados de validación.
Análisis estocástico del CRFC de la orientación aleatoria de la fibra
El objetivo de la mecánica estocástica es el de analizar la dispersión de una variable aleatoria obtenida de las leyes de la mecánica determinista en cada evento o dato de muestreo (Ostoja-Starzewski, 2008).
Cada evento 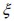 corresponde a un análisis determinista del problema donde se ha escogido un valor aleatorio de la orientación de la fibra
corresponde a un análisis determinista del problema donde se ha escogido un valor aleatorio de la orientación de la fibra 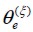 por elemento finito. La colección de los resultados obtenidos en este evento se indica de la forma
por elemento finito. La colección de los resultados obtenidos en este evento se indica de la forma 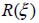 .
.
El análisis estocástico repite el problema determinista conformando un grupo de eventos en el espacio de muestreo de tamaño m y estudia la dispersión del campo de los resultados definido como:
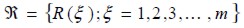 | (15) |
De esta forma, cada vez que se resuelve el problema determinista se llega a una solución distinta. Por ejemplo, la energía de deformación de una probeta sometida a presión uniforme es diferente en cada evento, no obstante todo valor de energía es mayor que la energía de deformación dada cuando las fibras están orientadas perpendicularmente a la carga y es menor que la energía de deformación si las fibras son paralelas a ella.
En el modelo del concreto reforzado con fibras cortas se espera que la dispersión de los resultados disminuya con el aumento del tamaño del espacio de muestreo m y con el incremento de la densidad de la malla de elementos finitos. En consecuencia, el comportamiento ortótropo de dirección material aleatoria que tiene el CRFC en cada punto material se convierte en un comportamiento isótropo en el volumen del elemento estructural. El modelo se implementó sobre el programa de elementos finitos a código abierto PEFiCA (Linero, 2010).
Módulo de elasticidad equivalente a un material isótropo
Como ejemplo de validación del modelo se analizó un panel cuadrado de lado L y espesor t hecho de concreto reforzado con fibras cortas, sometido a una carga distribuida por unidad de área q sobre uno de los lados, como se ilustra en la figura 3(a).
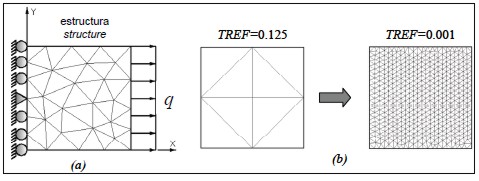
Figura 3. panel sometido apresión uniforme: (a) esquema genral, (b)mallas de elementos finitos.
Se ha utilizado un coeficiente de participación volumétrica del acero 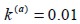 , el cual representa un contenido habitual de fibras de acero en matrices de concretos estructurales. Dicha cuantía corresponde a una relación entre los módulos de elasticidad en las direcciones materiales
, el cual representa un contenido habitual de fibras de acero en matrices de concretos estructurales. Dicha cuantía corresponde a una relación entre los módulos de elasticidad en las direcciones materiales 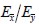 cercanos a un valor de La energía de deformación del sólido en un evento
cercanos a un valor de La energía de deformación del sólido en un evento 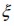 es el resultado de la sumatoria de las energías de deformación de cada uno de los elementos finitos de la malla obtenida de la forma:
es el resultado de la sumatoria de las energías de deformación de cada uno de los elementos finitos de la malla obtenida de la forma:
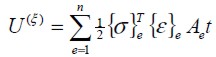 | (16) |
siendo n el número de elementos finitos, y 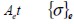 , y
, y 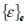 el volumen, el vector de esfuerzo y de deformación del elemento, respectivamente.
el volumen, el vector de esfuerzo y de deformación del elemento, respectivamente.
Por otro lado, de forma analítica la energía de deformación de un panel elástico isótropo equivalente de dimensiones 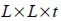 sometido a una presión q uniforme, es igual a:
sometido a una presión q uniforme, es igual a:
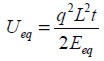 | (17) |
donde 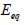 es el módulo de elasticidad equivalente a un material isótropo.
es el módulo de elasticidad equivalente a un material isótropo.
Igualando la energía de deformación calculada en un evento 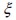 a partir de la ecuación (16) con la energía equivalente de un modelo isótropo indicada en la ecuación (17), se puede expresar el módulo de elasticidad equivalente a un material isótropo en el evento
a partir de la ecuación (16) con la energía equivalente de un modelo isótropo indicada en la ecuación (17), se puede expresar el módulo de elasticidad equivalente a un material isótropo en el evento 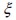 como:
como:
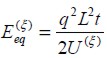 | (18) |
El valor promedio 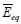 y la desviación estándar
y la desviación estándar 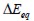 del módulo de elasticidad equivalente del conjunto de eventos realizados corresponden a:
del módulo de elasticidad equivalente del conjunto de eventos realizados corresponden a:
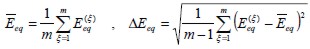 | (19) |
Para obtener el módulo 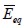 y su dispersión se simuló el problema con 5 mallas de diferente densidad y con campos de muestreo m hasta de 250 eventos. El tamaño relativo del elemento finito TREF está definido como el cociente entre el área del elemento finito
y su dispersión se simuló el problema con 5 mallas de diferente densidad y con campos de muestreo m hasta de 250 eventos. El tamaño relativo del elemento finito TREF está definido como el cociente entre el área del elemento finito 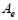 y el área de la estructura modelada
y el área de la estructura modelada 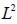 , de tal forma que la malla utilizada más densa corresponde a
, de tal forma que la malla utilizada más densa corresponde a 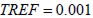 y en la malla menos densa
y en la malla menos densa 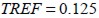 , como lo muestra la figura3 (b).
, como lo muestra la figura3 (b).
El valor promedio y la desviación estándar del módulo de elasticidad equivalente dividido entre el módulo de Young de la matriz de concreto 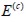 se indican en la figura 4 .
se indican en la figura 4 .
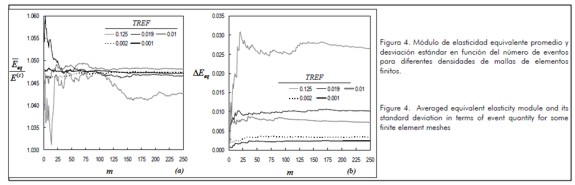
Allí se demuestra que, a medida que crece el tamaño del campo de muestreo, disminuye la dispersión de 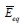 . Por ejemplo, para
. Por ejemplo, para 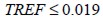 y tamaño de muestras m de 30 eventos la desviación estándar del módulo elástico equivalente es menor al 1%. Asimismo, la densidad de la malla reduce la dispersión de los resultados, como lo indican la desviación estándar del 3% en la malla menos densa y del 0,2% en la malla más fina.
y tamaño de muestras m de 30 eventos la desviación estándar del módulo elástico equivalente es menor al 1%. Asimismo, la densidad de la malla reduce la dispersión de los resultados, como lo indican la desviación estándar del 3% en la malla menos densa y del 0,2% en la malla más fina.
Ejemplo de aplicación: viga de tres puntos
Se simuló el comportamiento elástico de una viga de concreto reforzado con fibras cortas con una entalla en la mitad de la luz, sometida a una carga puntual 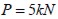 , como se indica en la figura 5 (a) (Ferrara y Gettu, 2000). La viga tiene una altura
, como se indica en la figura 5 (a) (Ferrara y Gettu, 2000). La viga tiene una altura 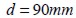 , una longitud
, una longitud 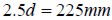 , un espesor de
, un espesor de  y el ancho de la entalla fue de 2,5 mm y el largo de ésta de 23,13 mm.
y el ancho de la entalla fue de 2,5 mm y el largo de ésta de 23,13 mm.
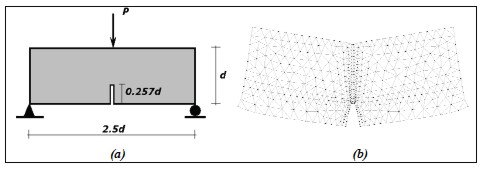
Figura 5. Viga de tres puntos: (a) esquema general, (b) malla de elementos finitos deformada
Las características mecánicas de la matriz de concreto simple son las siguientes: módulo de Young 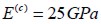 , relación de Poisson
, relación de Poisson 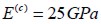 y resistencia a la compresión
y resistencia a la compresión 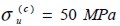 . En cambio, las fibras cortas de acero tienen un módulo de Young
. En cambio, las fibras cortas de acero tienen un módulo de Young 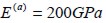 , una relación de Poisson
, una relación de Poisson 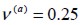 y un esfuerzo de fluencia
y un esfuerzo de fluencia 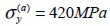 ; asimismo, su coeficiente de participación volumétrica k(a) es igual a 0,01, su longitud l es de 60 mm y su diámetro D es de 2 mm.
; asimismo, su coeficiente de participación volumétrica k(a) es igual a 0,01, su longitud l es de 60 mm y su diámetro D es de 2 mm.
Aplicando la ecuación (9) para una relación 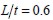 , se obtiene un factor de eficiencia por la dirección de la fibra fuera del plano
, se obtiene un factor de eficiencia por la dirección de la fibra fuera del plano 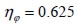 .
.
El área de la sección transversal de cada fibra es de 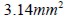 , por lo tanto para una cuantía
, por lo tanto para una cuantía 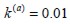 el área total de la sección transversal es igual a
el área total de la sección transversal es igual a 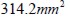 y el área transversal de la matriz de concreto es de
y el área transversal de la matriz de concreto es de 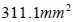 . Suponiendo una sección transversal total cuadrada, la separación mínima entre dos fibras vecinas paralelas R será igual al lado de tal cuadrado, es decir
. Suponiendo una sección transversal total cuadrada, la separación mínima entre dos fibras vecinas paralelas R será igual al lado de tal cuadrado, es decir 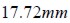 . Obtenidas las relaciones y
. Obtenidas las relaciones y 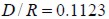 , y
, y 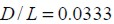 el factor de eficiencia por variación de esfuerzos en los extremos de la fibra
el factor de eficiencia por variación de esfuerzos en los extremos de la fibra 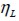 es igual a 0,8176.
es igual a 0,8176.
Se dividió el medio con 883 elementos triangulares lineales correspondientes a un factor TREF= 0,00113 y se realizaron 25 eventos de orientación aleatoria de fibras. En uno de los eventos, la geometría deformada y los esfuerzos principales 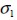 de la viga se ilustran en las figuras 5(b) y 6 .
de la viga se ilustran en las figuras 5(b) y 6 .
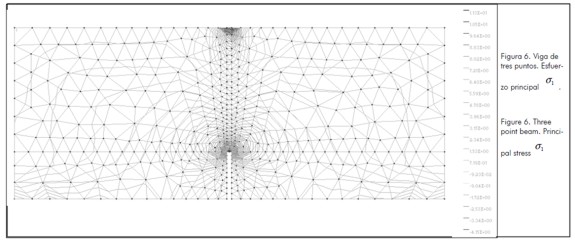
El número de muestras elegido obedece a la baja desviación estándar observada en el ensayo uniaxial para tamaño relativo de elemento finito TREF entre 0,001 y 0,002, como lo indica la figura 4 .
De un análisis estocástico de los resultados de la deflexión en la mitad de la luz δ y del esfuerzo principal máximo en tracción 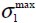 se obtuvo un valor promedio de la deflexión
se obtuvo un valor promedio de la deflexión 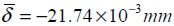 con una desviación estándar del 0.05%, y un valor medio del esfuerzo
con una desviación estándar del 0.05%, y un valor medio del esfuerzo 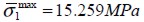 con una desviación estándar del 0.85% .
con una desviación estándar del 0.85% .
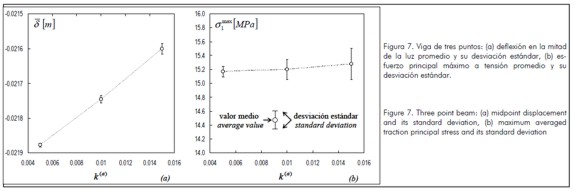
Adicionalmente, analizando la viga de tres puntos con coeficientes de participación volumétrica de 0,005 y de 0,015, también se obtuvieron deflexiones y esfuerzos medios con dispersiones muy pequeñas, como lo indica la figura 7 .
Conclusiones
El modelo presentado permite reproducir el comportamiento elástico de elementos estructurales de concreto reforzado con fibras cortas mediante dos rangos de análisis: un análisis determinista, en el cual cada elemento finito está asociado a un material compuesto de dirección material aleatoria, y un análisis estocástico, donde se coleccionan los eventos obtenidos de los resultados del análisis determinista y se estudia su dispersión con respecto a los valores promedio.
El comportamiento elástico del CRFC se obtiene de cuatro propiedades de los materiales componentes: el módulo de Young y la relación de Poisson de la matriz de concreto simple, y el módulo de Young y el coeficiente de participación volumétrica de las fibras de acero.
Mediante el modelo descrito se demuestra que el comportamiento ortótropo de dirección material aleatoria de cada punto del cuerpo se puede representar como un comportamiento isótropo aproximado del elemento estructural.
En el análisis estocástico el tamaño del campo de muestreo determina la dispersión de la respuesta. En la obtención del módulo de elasticidad equivalente promedio, a medida que aumenta tamaño del campo de muestreo la desviación estándar se reduce, sin embargo esta disminución tiene una asíntota determinada por la densidad de la malla. A mallas más finas se requiere un campo muestral menor para obtener desviaciones estándar constantes más bajas.
Por medio de este modelo se pueden simular ensayos experimentales de elementos estructurales con el fin de determinar desplazamientos, deformaciones y esfuerzos promedios, con sus respectivas desviaciones estándar. Como aplicación se simuló el comportamiento de una viga entallada con una carga puntual en el centro de la luz, con tres cantidades diferentes de fibras de refuerzo, obteniendo desviaciones estándar menores al 0,1% en su deflexión.
Agradecimientos
Los autores agradecen la financiación recibida por la Dirección Nacional de Investigación de la Universidad Nacional de Colombia, mediante el proyecto DIB – 7006.
Nomenclatura
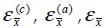 Deformaciones longitudinales del concreto, del acero y del material compuesto en dirección de la fibra.
Deformaciones longitudinales del concreto, del acero y del material compuesto en dirección de la fibra.
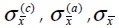 Esfuerzo normal del concreto, del acero y del material compuesto en dirección de la fibra.
Esfuerzo normal del concreto, del acero y del material compuesto en dirección de la fibra.
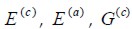 Módulo de Young del concreto y del acero y módulo de cortante del concreto.
Módulo de Young del concreto y del acero y módulo de cortante del concreto.
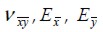 Relación de Poisson y módulos de elasticidad paralelo y perpendicular a la fibra del material compuesto.
Relación de Poisson y módulos de elasticidad paralelo y perpendicular a la fibra del material compuesto.
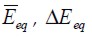 Valor promedio y desviación estándar del módulo de elasticidad equivalente del conjunto de eventos realizados.
Valor promedio y desviación estándar del módulo de elasticidad equivalente del conjunto de eventos realizados.
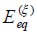 Módulo de elasticidad equivalente a un material isótropo en el evento
Módulo de elasticidad equivalente a un material isótropo en el evento 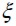 .
.
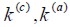 Fracciones de participación volumétrica de la matriz de concreto y de las fibras de acero.
Fracciones de participación volumétrica de la matriz de concreto y de las fibras de acero.
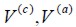 Volúmenes de concreto y de las fibras de acero contenidos en un volumen de referencia del material compuesto.
Volúmenes de concreto y de las fibras de acero contenidos en un volumen de referencia del material compuesto.
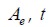 área y espesor del elemento finito.
área y espesor del elemento finito.
L, D, R Longitud, diámetro y separación promedio de la fibra corta.
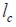 Longitud de interfase de la fibra corta, distancia en la cual alcanza su esfuerzo de tensión promedio.
Longitud de interfase de la fibra corta, distancia en la cual alcanza su esfuerzo de tensión promedio.
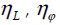 Factores de eficiencia del comportamiento como fibra corta y de probabilidad de orientación de las fibras fuera del plano del panel de concreto.
Factores de eficiencia del comportamiento como fibra corta y de probabilidad de orientación de las fibras fuera del plano del panel de concreto.
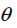 ángulo de orientación de la fibra en el plano xy formado entre los ejes x y
ángulo de orientación de la fibra en el plano xy formado entre los ejes x y 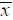 , y fuera del plano xy, respectivamente.
, y fuera del plano xy, respectivamente.
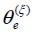 ángulo de orientación de la fibra dentro del plano para el elemento finito (e) en el evento
ángulo de orientación de la fibra dentro del plano para el elemento finito (e) en el evento 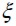 .
.
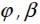 ángulo de orientación de la fibra fuera del plano xy del sólido y ángulo máximo de orientación de la fibra fuera del plano xy, si el espesor del mismo es inferior a la longitud total de la fibra.
ángulo de orientación de la fibra fuera del plano xy del sólido y ángulo máximo de orientación de la fibra fuera del plano xy, si el espesor del mismo es inferior a la longitud total de la fibra.
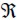 Campo de resultados obtenido del análisis.
Campo de resultados obtenido del análisis.
m Cantidad de eventos 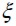 en el campo de resultados.
en el campo de resultados.
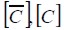 Matriz constitutiva elástica en coordenadas materiales y en coordenadas globales, respectivamente.
Matriz constitutiva elástica en coordenadas materiales y en coordenadas globales, respectivamente.
[ T ] Matriz de transformación en términos del ángulo θ.
q Carga aplicada por unidad de área sobre uno de los lados del sólido.
TREF Tamaño relativo del elemento finito.
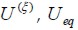 Energía de deformación del sólido en un evento
Energía de deformación del sólido en un evento 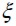 y energía equivalente calculada analíticamente para un sólido elástico isótropo.
y energía equivalente calculada analíticamente para un sólido elástico isótropo.
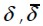 Deflexión y deflexión promedio en la mitad de la luz de la viga.
Deflexión y deflexión promedio en la mitad de la luz de la viga.
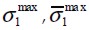 Esfuerzo principal máximo a tracción del compuesto y su valor promedio, respectivamente.
Esfuerzo principal máximo a tracción del compuesto y su valor promedio, respectivamente.
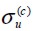 Resistencia a la compresión del concreto empleado en el ensayo de la viga.
Resistencia a la compresión del concreto empleado en el ensayo de la viga.
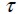 Esfuerzo cortante actuante sobre la superficie de la fibra cuando ésta se encuentra sometida a la tensión de falla.
Esfuerzo cortante actuante sobre la superficie de la fibra cuando ésta se encuentra sometida a la tensión de falla.
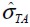 Resistencia de la fibra a tracción.
Resistencia de la fibra a tracción.
Referencias
ACI, Technical Report ACI 544.2R., Measurement of Properties of Fiber Reinforced Concrete., United States of America, 1989. [ Links ]
ACI, Technical Report ACI 544.1R., State of the Art Report on Fiber Reinforced Concrete., United States of America, 1996. [ Links ]
ACI, Technical Report ACI 506.1R., Committee Report on Fiber Reinforced Shotcrete., United States of America, 1998. [ Links ]
Dvorak, G., Bahei-el-Din, Y., Plasticity analysis of fibrous composites., Journal of Applied Mechanics, Vol. 49, 1982, pp. 327-335. [ Links ]
Ferrara, L., Gettu, R., Non-local damage analysis of three-point bending tests on SFRC notched beams., Fifth RILEM symposium on fibre-reinforced concrete (FRC), 2000, pp. 357-367. [ Links ]
Hughes, T. J. R., The finite element method., New York, Dover, 2000. [ Links ]
Linero, D., PEFiCA - Programa de elementos finitos a código abierto. versión 1.0., Bogotá, Universidad Nacional de Colombia, 2010. [ Links ]
Matthews, F. L., Rawlings, R. D., Composite materials: engineering and Science., Cambridge, Woodhead Publishing Limited, 1994. [ Links ]
Oller, S., Simulación numérica del comportamiento mecánico de los materiales compuestos., Barcelona, CIMNE, 2003. [ Links ]
Oñate, E., Structural Analysis with the Finite Element Method., CIMNE - Springer, 2009. [ Links ]
Oñate, E., Zárate, F., Cálculo de estructuras por el método de los elementos finitos., Barcelona, Centro Internacional de Métodos Numéricos en Ingeniería, 1995. [ Links ]
Ostoja-Starzewski, M., Microestructural randomness and scaling in mechanics of materials., Boca Raton, USA, Chapman & Hall/CRC, 2008. [ Links ]
Weaver, J., Johnson, C., Finite elements for structural analysis., New Jersey, Prentice Hall, 1984. [ Links ]











 text in
text in 


