Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.31 no.1 Bogotá Jan./Apr. 2011
Two Two-dimensional wood drying stress simulation using control control-volume mixed finite element methods ( CVFEM)
Carlos Salinas1, Cristian Chávez2, Yerko Gatica3,Rubén Ananias4
1Ph. D., in Science. Associate Professor, Department of Mechanical Engineering, Universidad del Bio-Bio, Chile. casali@ubiobio.cl
2 M.Sc. Candidate in Science and Technology of Wood, Universidad del Bio-Bio, Chile. crchavez@alumnos.ubiobio.cl
3Ph.D. Candidate Science & Industry Wood, Universidad del Bio-Bio, Chile. ygatica@ubiobio.cl
4Ph. D. in Wood Science. Associate Professor, Department of Wood Engineering, Universidad del BioBio, Chile. ananias@ubiobio.cl
ABSTRACT
The work was aimed at simulating two-dimensional wood drying stress using the control-volume finite element method (CVFEM). Stress/strain was modeled by moisture content gradients regarding shrinkage and mechanical sorption in a cross-section of wood. CVFEM was implemented with triangular finite elements and lineal interpolation of the independent variable which were programmed in Fortran 90 language. The model was validated by contrasting results with similar ones available in the specialised literature. The present model's results came from isothermp><b>al (20ºC) drying of quaking aspen (Populus tremuloides): two-dimensional distribution of stress/strain and water content, 40, 80, 130, 190 and 260 hour drying time and evolution of normal stress ( -2,5<σxx<1.2, MPa ),from the interior to the exterior of wood.
Keywords: simulation, drying, wood, stress, creep,CVFEM.
Received: August 21th 2009. Accepted: Feuary 10th 2011
Introduction
The work describes modelling and simulating solid wood drying focused on mass transfer (sorption) and stresses caused by drying. A collection of relevant work was found in Turner and Mujumdar (1997). The paper deals with two major aspects: moisture transport, modelled based on the water potential concept which has been widely discussed in previous work (Salinas et al., 2004 and 2011) and drying stress distribution associated with moisture content (this work's main objective).
Theory says that wood shrinkage during drying induces mechanical stress developing throughout the structure (McMillen, 1963); such stress is affected by changes in moisture content, mechanical restraint, anisotropy and the viscoelastic behaviour of wood (Young, 1957). It has been noted that moisture gradients have favour the development of hydro-mechanicl stress, this bing as much or more important than plastic deformation (Keey et al., 2000).
The proposed model has thus been focused primarily on strain caused by mass transport (moisture content) in wood. Perre et al., (1993), Chen et al., (1997), Stevensson and Martensson (2002), Kang et al., (2004) and Pang (2007) have all proposed one-dimensional models for determining the drying stress caused by shrinkage and mechanical sorption. Likewise, twodimensional models for the strains have been proposed by authors such as Turner and Ferguson (1995), Stevensson and Martensson (1996), Ferguson (1998), Perre and Turner (2001), Thuvander et al., (2002), Cheng et al., (2007), as well as threedimensional models by Ormarsson et al., (2003), Remond et al., (2006), and Niemz Keuneke (2008).
This paper studied the strain and stress caused by moisture gradients during drying based on work by Turner Ferguson (1995). It was thus proposed to integrate the partial differential equation model using the control-volume finite element method (CVFEM) developed by Baliga Patankar (1983). In particular, changes were made to the geometrical and physical parameters for analysing stability and consistency. These algorithms were validated by comparing this study's results with similar studies in the pertinent literature applied to the isothermal drying of solid quaking aspen wood (Populus tremuloides). Numerical data for transient twodimensional distribution of stress/strain is given.
Physical model
A model for the strain/stress produced when drying solid wood is presented. Non-uniform transient effects induced by variation of moisture content (M) was modelled: stress (sij), strain (eij) and displacement (u = (u, v) or ui con (i = 1,2)).
A two-dimensional cross-section of wood was studied in transverse plane (Figure 1); its properties are given in Table 1. An isothermal process was assumed for the orthotropic transport of moisture during drying and plane strain for strain/stress, the product of free deformation (shrinkage) and mechanical sorption caused by moisture gradients below fie saturation point (FSP).
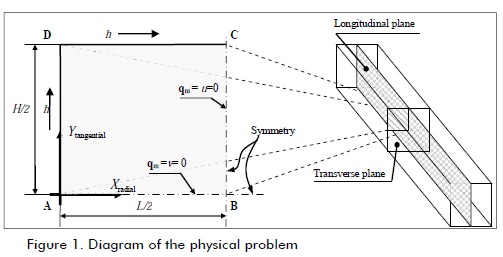
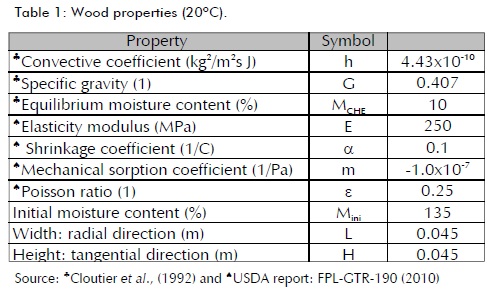
Initial and boundary conditions were as follows. An initial moisture M= Mini, with Neumann-type boundary conditions with non-flow on the symmetry axis (x = L/2 and y = 0) and convection on surfaces x = 0 and y = H/2 were considered for moisture transport. A non-deformed initial state (si =gij=ui =0) was assumed with Dirichlet boundary conditions on the symmetry axis (u=0 at x=L/2 and v=0 at y=0) and free on surfaces x=0 and y=H/2 for tstrain/stress.
The rheological model was based on work performed by Ferguson (1997 1998) where creep was described as:
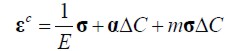 | (1.1) |
leading to the next kind of deformation: elastic (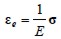 ), free shrinkage (
), free shrinkage ( 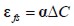 ) and mechanical sorption (
) and mechanical sorption (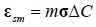 ).
).
Mathematical model
The mathematical moisture transport model used in this work was based on the water potential concept (ψ), like the model proposed by Cloutier Fortin (1994) and implemented in numerical form in Salinas et al., (2004). Taking moisture content (M) as independent variable in the above can be summarised in the following expression:
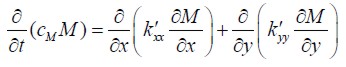 | (1.2) |
where 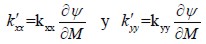 conductivities of M
conductivities of M , capacity
, capacity 
CM ,Kxx y Kyy were functions of moisture content M and temperature T.
The mathematical model for two-dimensional deformation resulting from applied mechanical equiliium at every point in the absence of body force can be described as:
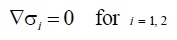 | (1.3) |
where 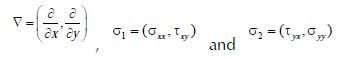
The products of non-uniform distribution of moisture were induced stress due free deformation and mechanical sorption. Such stresses was modelled by five implicit-function parameters: initial strain 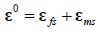 , shrinkage a, mechanical sorption m, stress s, change in concentration DC and Poisson ratio n:
, shrinkage a, mechanical sorption m, stress s, change in concentration DC and Poisson ratio n:
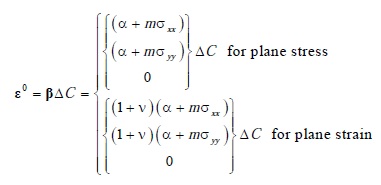 | (1.4) |
Thus, stresses were determined from the following expression:
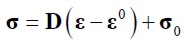 | (1.5) |
where σo represented initial stress data and D the constitutive matrix.
 | (1.6) |
The problem was integrated using the Initial Strain Method, Zienkiewicz Taylor (2000). DC was thus defined as moisture variation between time 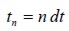 and
and 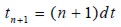 , , where dt was the time interval considered, i.e.
, , where dt was the time interval considered, i.e. 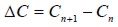 and similarly
and similarly 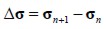 and
and 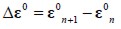 . Thus:
. Thus:
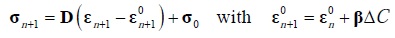 | (1.7) |
Numerical model
The numerical model applied to the displacement equation for the problem directly related to stress/strain is shown below; a similar procedure has been performed for the moisture transport equation (1.2) given in Salinas et al., (2011).
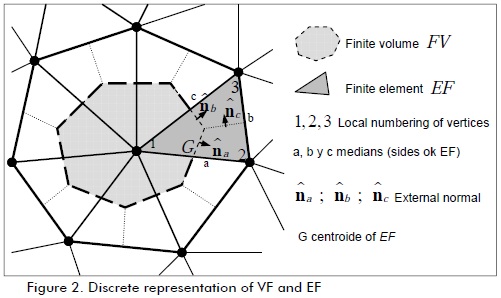
Considering that domain ε formed nl finite volume (FV)(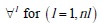 ) contour Ωl and similarly, each VF was composed by nk partial contributions of finite element (FE) with boundary
) contour Ωl and similarly, each VF was composed by nk partial contributions of finite element (FE) with boundary 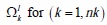 (see Figure 2), then
(see Figure 2), then
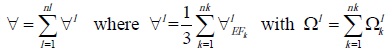 | (1.7) |
Consequently, the integral of (1.3) in subdomain  , according to Green's theorem, was equal to flux divergence on boundary Ω1, i.e.
, according to Green's theorem, was equal to flux divergence on boundary Ω1, i.e.
 | (1.9) |
Where
were stresses with i=1,2: stresses in x and y direction, respectively and  the external normal unit vector for Ω1.
the external normal unit vector for Ω1.
Joint solution (system of equations) led to discrete values for the independent variable involved (displacement u).
Each VF was formed by partial contributions of nk EF (Figure 2). Thus, the partial contribution of EF k to VF focused on local node 1 (global l) was:
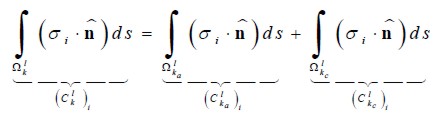 | (1.10) |
Where subscript a and b represented contour segments 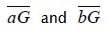 , respectively.
, respectively.
Considering the value of σi at the midpoint for each segment was equal to 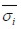 as dominant in that segment and incorporating the definitions given in (1.3), then:
as dominant in that segment and incorporating the definitions given in (1.3), then:
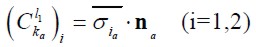 | (1.11) |
where 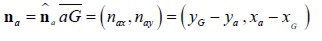 On the other hand, redefining stresses σi as functions of linear strains εii and angular stress ϒij as:
On the other hand, redefining stresses σi as functions of linear strains εii and angular stress ϒij as:
 | (1.12) |
where 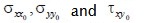 were initial stresses.
were initial stresses.
Deformation εii and ϒij described in terms of displacement 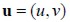 were:
were:
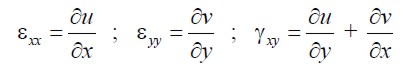 | (1.13) |
Where as, for the previous integration, a linear variation of u within the EF, of the form:
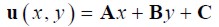 | (1.14) |
where A,B,C were constants defined in terms of nodal displacements u1,u2 y u3, equal to:
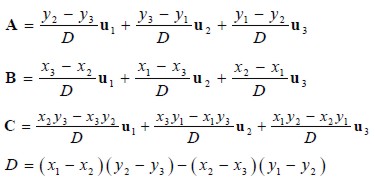
Displacement variation would thus be:
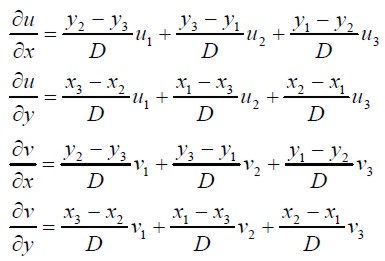 | (1.15) |
Introducing the definitions given by equations (1.12) to (1.15), contribution 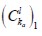 may be expressed in terms of nodal values of displacement as:
may be expressed in terms of nodal values of displacement as:
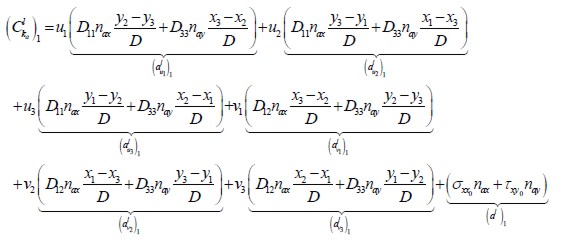 | (1.16) |
A similar expression may be obtained for  .
.
Similar expressions for segment contributions  equal to
equal to  , given by (1.16), for segments
, given by (1.16), for segments 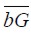 and
and 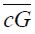 equal to
equal to 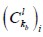 and
and 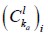 can be obtained simply by exchanging normal vector na by nb or nc as appropriate.
can be obtained simply by exchanging normal vector na by nb or nc as appropriate.
Taking the definitions given in (1.10) and incorporating developments (1.16):
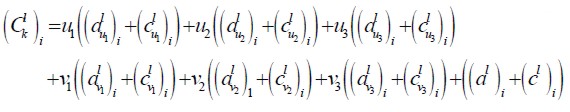 | (1.17) |
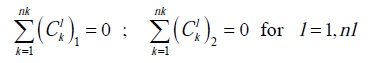 | (1.18) |
The following system of equations was written:
Two algeaic equations were thus obtained for each l value; one for each component of the average displacement 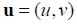 in each subdomain εl, all of which constitutes a
in each subdomain εl, all of which constitutes a 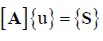 2nL x 2nL type linear system of equations.
2nL x 2nL type linear system of equations.
Results
Diffusion of heat and thermal stress in a steel plate
The transient simulation of plane stress was considered in a twodimensional plate undergoing non-uniform transient heating (Figure 3); properties are given in Table 2. Magnitudes were L = 0.6 (m) length and H = 0.2 (m) height. The following were considered for boundary condition purposes: constrained displacement in direction Y in segment AD (v = 0 at y = 0), constrained in direction X on section BC (u = 0 at x = L) and free CD and LD segments. Naturally, point B was constrained in X and Y ((u,v) = (0,0) in B). The above problem has been dealt with by Boley and Weiner (1960).
Figure 3. Two-dimensional plate with transient non-uniform temperature variation

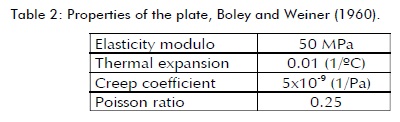
Transient non-uniform temperature distribution T (ºC) as an exponential function of y (m) coordinate and time t (h) given by:
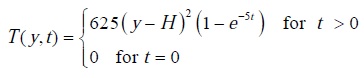 | (1.19) |
Product of non-uniform distribution of temperature occurring with stress induced by sustained expansion (creep). Such effect can be modelled with the same model and stress presented for moisture. Initial deformation ε0 was based on the following parameters: thermal expansion a, creep coefficient m, stress s, temperature variation DT and for plane strain Poisson ratio n.
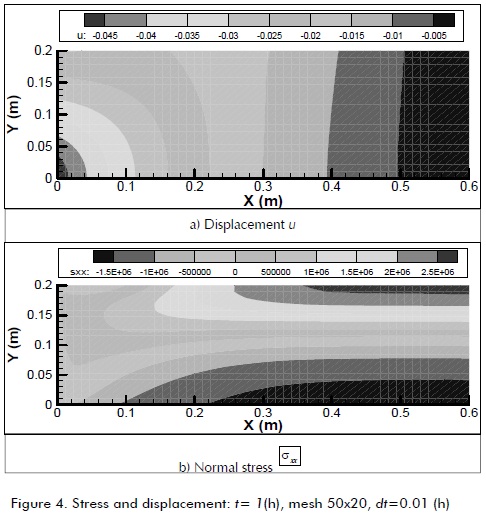
Figure 4 shows the mapping of the strain/stress state for t = 1 (h) (steady state). Consistency in imposing boundary conditions can be seen in such mapping (displacement given in Figure 4a). The effects of restriction on free deformation in the development of normal stresses can be seen in Figure 4b
Analysis of convergence and consistency regarding mesh type contrasted with analytical solution is shown in Figure 5, showning that transient convergent results can be achieved with 52x20 uniform mesh.
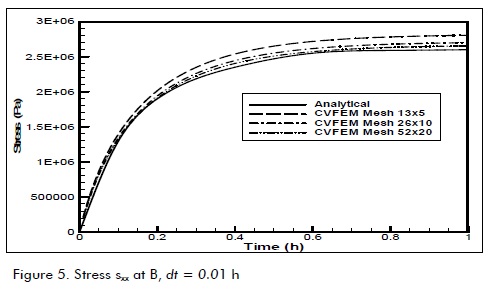
Figure 6 shows analysis of consistency in terms of time compared to convergent solution in segment BC. Good convergence was observed for 0.001 (h) time steps.
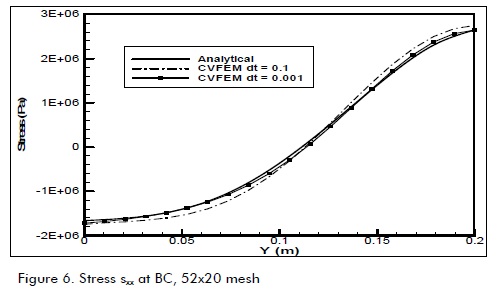
Moisture transport and drying stress in quaking aspen wood
Non-uniform transient simulation of moisture transport in wood inducing stress and strain was considered. Each integration time for moisture distribution was thus determined (as described in Salinas et al., 2004), giving free deformation, and then (ε0) encouraging displacement and stress was calculated (the latter was then calculated as being uncoupled, according to Zienkiewicz and Taylor’s initial deformation method, 2000). Consistency analysis revealed that meshes having refinement exponential to surface convection could capture moisture gradients having a smaller number of discrete elements.
Figure 7 shows spatial distribution for drying times regarding stress/strain calculation. Figure 7a shows moisture content transient and spatial distribution having the greatest gradients (concentration of iso-lines) around 60% M. Orthotropic drying pattern was reflected in the lack of drying front symmetry. Figure 7b shows radial displacement (u), showing the correct implementation of boundary conditions, largest displacements being concentrated at the edges, constrained to one degree of freedom.
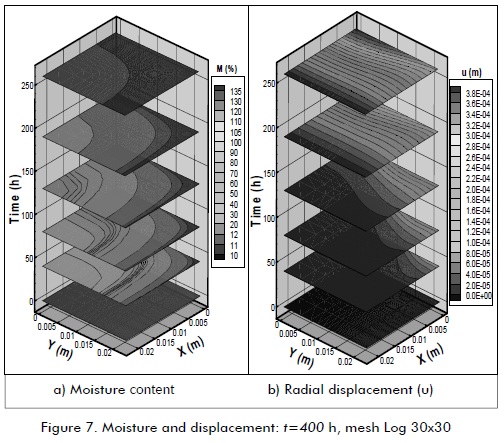
Figure 8a shows in detail the residual normal stress of radial drying out. It can been observed that the main efforts were concentrated on A, B and C (see Figure 1), being in tension in A and C (surface) and compression in B (centre). The shear stresses shown in Figure 8b were concentrated on the diagonal, slightly shifted towards point D (surface).
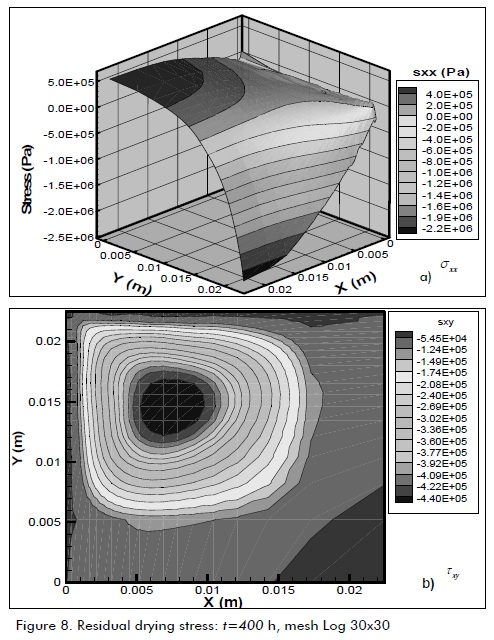
Figure 9 highlights in detail the transient evolution of normal radial stress on section BC where its complex evolution according to simulated drying stress stages can been appreciated. Figure 9a shows the first stage of drying characterised by increasing development of tension on the wood surface by contrast with compression in the centre of it. As a complement, Figure 9b shows the second stage characterised by increasing reversal stress
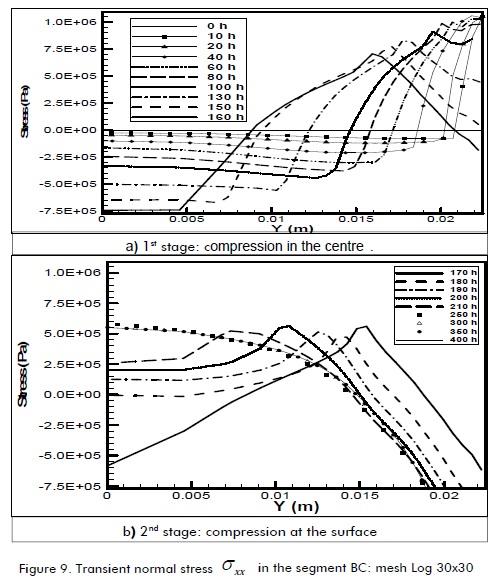
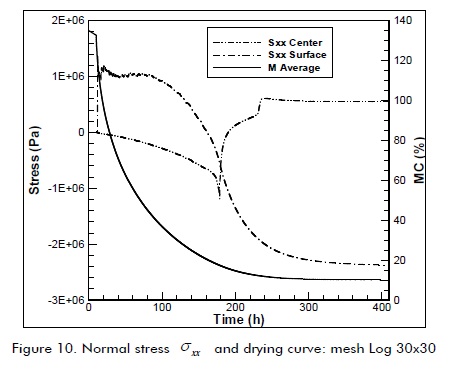
Figure 10 shows the transient changes in kind of stress in the centre and at the surface of the domain of calculation (point B and C, Figure 1); it shows the dynamics of change in normal radial stress intensity correlated with moisture content. There was marked tension and compression at the beginning of drying, on the surface and in the centre, respectively. This contrasted with final stress at the end of drying in which normal stresses were reversed. The latter is an important qualitative feature of the physical problem being simulated. It highlighted the singular strong transient stress developed during drying at t = 195 (h) with CH = 10%.
Conclusions
The results presented in Figures 4-7 led to concluding that the algorithm developed here generated effective simulations of stress/strain caused by free deformation and sustained stress. Consistency analysis of mesh size and time steps inferred that simulation can be achieved with 20x52 mesh and 0001 time steps (h).
The results presented in Figures 8-10 led to concluding that the qualitative features present in wood drying had been simulated (i.e. regions subjected to tension and compression during transitional drying, resulting in residual drying stress characterised by tension on the surface and compression in the centre of the wood). Moreover, accepting the validation of numerical analysis on the thermal plate, the quantitative values of simulated wood drying should be very similar to physical properties. Naturally, it would be desirable to corroborate experimental data, which has been left for future work.
References
Baliga B. R., Patankar S. V., A new finite element formulation for convection diffusion problems., Numerical Heat Transfer, Vol. 3, 1980, pp. 393-409. [ Links ]
Boley B. A., Weiner J. H, Theory of Thermal Stresses., John Wiley and Sons, Inc., New York, 1960. [ Links ]
Chen G, Keey, R.B, Walker J.F.C., The drying stress and check development on high-temperature kiln seasoning of sapwood Pinus radiate boards., Holz als Roh-und Werkstoff, Vol. 55, Nº 2, 1997, pp. 59-64. [ Links ]
Cheng, W., Morooka, T., Wu, Q., Liu, Y., Characterization of tangential shrinkage stresses of wood during drying under heated steam above 100 ºC., Forest Prod. J, Vol. 57, Nº 11, 2007, pp. 39-43. [ Links ]
Cloutier, A., Fortin, Y., Dhatt, G., A wood drying finite element model based on the water potential concept., Drying Technology, Vol. 10, No. 5: 1992, pp. 1151-1181. [ Links ]
Cloutier A., Fortin Y., Wood drying modeling based on the water potential concept: Effect of the hysteresis in the M-y relationship, Drying Tech., Vol. 12, Nº 8, 1994, pp. 1793-1814. [ Links ]
Ferguson, W.J., A control volume finite element numerical solution of creep problems., Int. J. Num. Meth. Eng, Vol. 40, No. 18, 1997, pp. 3463-3475 [ Links ]
Ferguson, W.J., A numerical prediction of the effect of airflow and wet bulb temperature on the stress development during convective wood drying., In mathematical modeling and numerical techniques in drying technology, Ed. I. Turner, A.S. Mujumdar, 1997, pp. 259-277. [ Links ]
Ferguson, W. J., The control volume finite element numerical solution technique applied to creep in softwoods., Int. J. Solid Structures, Vol. 35, No. 13, 1998, pp.1325-1338. [ Links ]
Kang, W., Lee, N., Jung, H., Simple analytical methods to predict one-an two-dimensional drying stresses and deformations in lumber., Wood Sci. Technol., Vol. 38, Nº 6, 2004, pp. 417- 428. [ Links ]
Keey, R., Langrish, T., Walker, J., Kiln-drying of lumber., Springer-verlag, N.Y. 2000. [ Links ]
Keunecke, D.S.H, Niemz, P., Three-dimensional elastic behaviour of common yew and Norway spruce., Wood Science and Technology, Vol. 42, Nº 8, 2008, pp. 633-647. [ Links ]
Mcmillen, J., Stresses in wood during drying., Res. Rap. 1652 USDA Forest Service. Forest Products Lab. Madison, WI., 1963. [ Links ]
Martensson, A., Stevensson, S., Application of a material model describing drying stresses in Word., 5th IUFRO International wood drying conference, 1996, pp. 93-102. [ Links ]
Ormarsson, S., Cown, D., Dahlblom, O., Finite element simulations de moisture related distortion in laminated timber products of norway spruce and radiata pine., 8th IUFRO International wood drying conference, 2003, pp. 27-33. [ Links ]
Pang, S., Mathematical modeling of kiln drying of softwood timber: Model development, validation and practical application., Drying Technology, Vol. 25, 2007, pp. 421-431. [ Links ]
Perre, P., Moser M., Matin, M., Advances in transport phenomena during convective drying with superheated steam and moist air., Int. J. Heat and Mass Transfer, Vol 36, Nº. 11, 1993, pp. 2725-2746. [ Links ]
Perre P., Turner, I., Determination of the material property variations across the growth ring of softwood for use in a heterogeneous drying model., Holzforschung, Vol. 55, Nº. 4, 2001, pp. 417-425. [ Links ]
Remond, R., Passard, J., Perre, P., The effect of temperature and moisture content on the mechanical behaviours of wood: a compressive model applied to drying and bending., European Journal of Mechanical Solid, Vol. 26, 2006, pp 558- 575. [ Links ]
Salinas, C., Ananias, R. A., Alvear, M., Simulación del secado convencional de la madera., Maderas Ciencia y Tecnología, Vol. 6, Nº. 1, 2004, pp. 3-18. [ Links ]
Salinas, C., Chávez, C., Gatica, Y., Ananias, R., Simulación del secado convencional de madera usando CVFEM., Revista Técnica de Ingeniería, Universidad de Zulia, vol. 34. Nº1, abril 2011. [ Links ]
Stevensson, S., Martensson, A., Simulation of drying stresses in wood Part III Convective air drying of sawn timber., Holz Roh Werkst, Vol. 60, 2002, pp. 72-80. [ Links ]
Thuvander, F., Kifetew, G., Berglund, L.A., Modeling of cell wall drying stresses in wood., Wood Sci. Technol., Vol. 36, 2002, pp.241-254. [ Links ]
Turner, I.W., Ferguson, W., An unstructured mesh cell-centered control volume method for simulating heat and mass transfer in porous media: Application to softwood drying, part I: The isotropic model., Appl. Math. Modeling, Vol. 19, 1995a, pp. 654-667. [ Links ]
Turner, I.W., Ferguson W., An unstructured mesh cell-centered control volume method for simulating heat and mass transfer in porous media: Application to softwood drying. Part II. The anisotropic model., Appl. Math. Modeling, Vol. 20, 1995b, pp. 669-674. [ Links ]
Turner, I., Mujumdar, A.S., Mathematical modeling and numerical techniques in drying technology., Marcel Dekker Inc., New York, ISBN 0-8247-9818-X, 1997, pp. 1-20. [ Links ]
USDA., Wood Handbook: Wood as un engineering material., report: FPL-GTR-190, 2010. [ Links ]
Young, R. The perpendicular to grain mechanical properties of red oak as related to temperature, moisture content and time., USDA, FPL-2079, Madison, USA,1957. [ Links ]
Zienkiewicz, O.C., Taylor R.L., The Finite Element Method., Fifth edition, published by Butterworth-Heinemann, Vol. 2. Solid Mechanics, 2000, pp. 365. [ Links ]











 text in
text in 


