Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.31 no.1 Bogotá Jan./Apr. 2011
Neural fuzzy digital filtering: multivariate identifier filters involving multiple inputs and multiple outputs (MIMO)
Juan Carlos García Infante1, José de J. Medel Juárez2, Juan Carlos Sánchez García3
1 Ph.D., Advanced Technology and Applied Science at the CICATA Legaria. Associated to SEPI, ESIME Culhuacán, Mexico.jcnet21@yahoo.com
2 Ph.D., Science in Automatic Control at the CINVESTAV. Associated to CIC, Mexico. jjmedelj@yahoo.com.mx
3 Ph.D., Digital Systems at the UAM Iztapalapa, Mexico. Associated to SEPI, ESIME Culhuacán, México. jcsanchezgarcia@gmail.com
ABSTRACT
Multivariate identifier filters (multiple inputs and multiple outputs - MIMO) are adaptive digital systems having a loop in accordance with an objective function to adjust matrix parameter convergence to observable reference system dynamics. One way of complying with this condition is to use fuzzy logic inference mechanisms which interpret and select the best matrix parameter from a knowledge base. Such selection mechanisms with neural networks can provide a response from the best operational level for each change in state (Shannon, 1948). This paper considers the MIMO digital filter model using neuro fuzzy digital filtering to find an adaptive parameter matrix which is integrated into the Kalman filter by the transition matrix. The filter uses the neural network as backpropagation into the fuzzy mechanism to do this, interpreting its variables and its respective levels and selecting the best values for automatically adjusting transition matrix values. The Matlab simulation describes the neural fuzzy digital filter giving an approximation of exponential convergence seen in functional error.
Keywords: digital filter, fuzzy control, neural network, MIMO, adaptive digital system.
Recibido: November 25th 2009
Aceptado: January 24th 2011
Introduction
An artificial neural network is a computational model which imitates a natural process such as a biological system. It has processing elements called neurons as in the human ain which are all interconnected, thereby constructing a neural network structure (Nikola, 1996; Medel et al., 2008). A fuzzy neural network classifies, searches for and associates information (Huang et al., 2006), giving a specific value in accordance with a desired reference signal. It constructs control volume described as
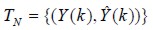
where 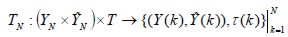 within membership intervals is delimited into a knowledge base (Schneider and Kandel, 1996).
within membership intervals is delimited into a knowledge base (Schneider and Kandel, 1996).
Fuzzy neural filter
Responses set into the knowledge base represent all possible correct filter responses (Gustafsson, 2000; Margaliot and Langholz, 2000; Zadeh, 1965) in accordance with an objective law, previously defined by actual natural references. The filtering mechanism selects the best response from the knowledge base when the state changes, using fuzzy (if-then) rules. The neural fuzzy filter is based on a back-propagation algorithm because its parameters are dynamically updated (Ali, 2003; Amble, 1987; Haykin, 1996), having different levels for each iteration (Huang, Zhu and Siew, 2006) using error described as E(k) (minimising it using 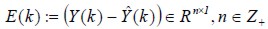 criterion in MIMO structure, this being the distance between the desired signal Y(k) and actual filter output
criterion in MIMO structure, this being the distance between the desired signal Y(k) and actual filter output 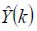 (García et al., 2008; Marcek, 2008). Figure 1 shows the filtering (Passino, 1998).
(García et al., 2008; Marcek, 2008). Figure 1 shows the filtering (Passino, 1998).
Error ((E(k))) has a limit interval [0, ε] and e is described as being a positive value in accordance with 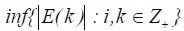 (i, is the index with k intervals) (Margaliot and Langholz, 2000)
( M o r a l e s , 2 0 0 2 ) . D e s c r i b e d a s : s u p
(i, is the index with k intervals) (Margaliot and Langholz, 2000)
( M o r a l e s , 2 0 0 2 ) . D e s c r i b e d a s : s u p 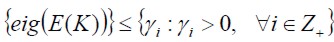 , where
, where 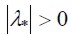 , sup
, sup 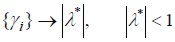 .
.
A neural fuzzy filter considers the following elements and concepts described in (Aaham, 1991; Ali, 2003; Gustafsson, 2000; Mamdani, 1974; Morales, 2002):
Fuzzy inference input. Filter input has metric sense description during this desired signal stage from reference system Y(k) (Ash, 1970);
Rule base: This is an inference set of filter input interprets using binary logic IF connector;
Inference mechanism: This is the expert consequence regarding the rule base for selecting membership function described as Ã(K) using the logic THEN connector (Yamakawa, 1989);
Activation function: This is the response filter stage transformed into a natural response. It is the best desired signal approximation value, previously described in the knowledge base; and
Natural updating: The filter process acquires the correct linguistic value and updates filter parameter values to a natural condition regarding the reference system, considering error difference between Y(K) and 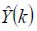 dynamically using functional error criterion J(K) (being the functional error matrix describing the real observed convergence value relationship and its estimation. I n r e c u r s i v e f o r m , t h i s i s :
dynamically using functional error criterion J(K) (being the functional error matrix describing the real observed convergence value relationship and its estimation. I n r e c u r s i v e f o r m , t h i s i s : 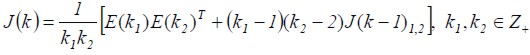 ).
).
Functional error is a dimensional quadratic matrix where 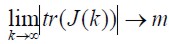 , having convergence in m if
, having convergence in m if 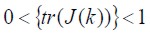 . The function is expressed in accordance with the second probability moment, its infimum value being described in (1).
. The function is expressed in accordance with the second probability moment, its infimum value being described in (1).
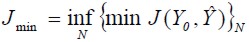 | (1) |
The neural fuzzy filter needs the knowledge base to select the corresponding response in accordance with the desired signal. Filtering first uses established fuzzy rules to infer or interpret the desired signal vector expressed as Y(K)(Takagi and Sugeno, 1986). The filter mechanism selects the correct variable in its data form and selects the level (the variable could be A temperature, B velocity or C pressure, respective levels being low, medium or high). The rules mechanism then selects the corresponding parameter Ã(K) to adjust the filter, thereby giving the correct vector response 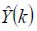 at filter output (Rajem and Gopal, 2006).
at filter output (Rajem and Gopal, 2006).
Parameter matrix properties
Multivariate neural fuzzy filter parameters 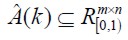 must fulfil conditions in accordance with the transition matrix:
It has dynamic transition matrix restriction operation: 1)
must fulfil conditions in accordance with the transition matrix:
It has dynamic transition matrix restriction operation: 1)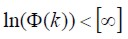 , 2)
, 2)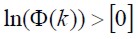 ,3)
,3)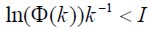 . Where ,
. Where , 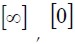 and I are a matrix described as infinity, null and identity, respectively. The estimator is described using the
transition matrix in (2):
and I are a matrix described as infinity, null and identity, respectively. The estimator is described using the
transition matrix in (2):
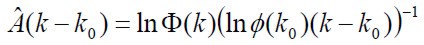 | (2) |
Change speed is limited within transition function (3 ):
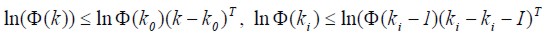 | (3) |
The transition matrix is bounded in 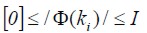 .
.
In accordance with the value for 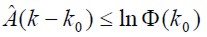 , the estimated parameter matrix complies with the difference in (4):
, the estimated parameter matrix complies with the difference in (4):
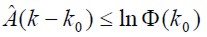 | (4) |
The Kalman filter (5) considered (4):
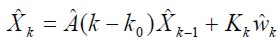 | (5) |
where Kalman matrix gain (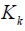 ) is a functional identification error, defined by the second probability moment between the desired signal and output recursive filter signal and
) is a functional identification error, defined by the second probability moment between the desired signal and output recursive filter signal and 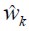 , represents noise.
, represents noise.
Results
The MIMO neural fuzzy filter considered Kalman filter structure (Hayking, 1996), the transition matrix being based on knowledge according to functional error criteria (Ash, 1970). A statistical software system considered evolution times bounded by PC with AMD Sempron 3100+ processor performance at k intervals, average evolution time being 0.004 sec ± 0.0002 sec. This paper used the first order differential and discrete ARMA model (6) to represent a reference system.
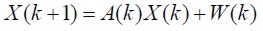 | (6) |
Output (7):
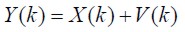 | (7) |
Where 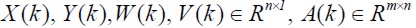
X(k) was the internal state vector, A(k) represented matrix parameters, W(k) was vector noise within the system, Y(k) was the reference vector desired system signal at filter input and V(k) was output vector noise.
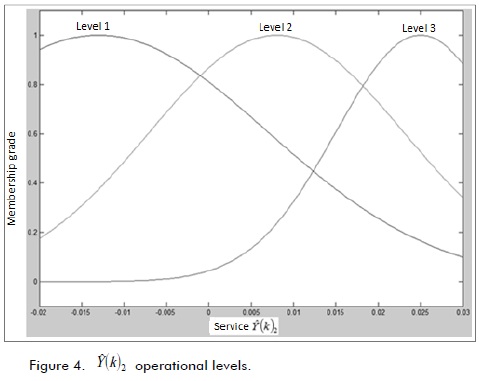
Operational levels were described for operation regarding functional error. Filtering gives each variable a linguistic description expressed as low, medium and high levels. Figure2 shows matrix parameter estimation given by 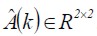
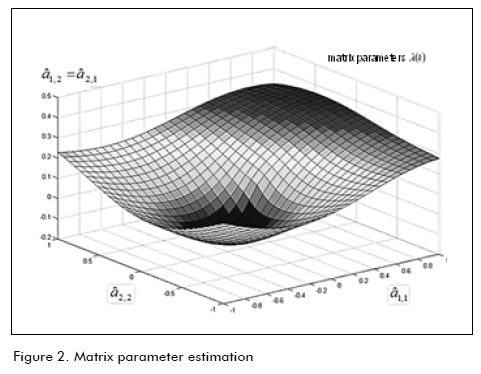
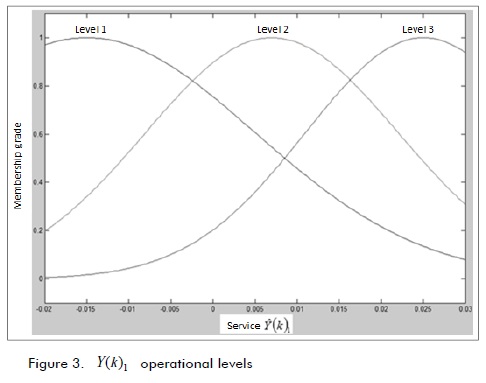
Considering matrix parameter estimation Ã(K) in (5), Figure 3
shows projected response levels at filter output  with desired signal Y(k)1. Figure 4 presents projection variables
with desired signal Y(k)1. Figure 4 presents projection variables  and Y(k)2.
and Y(k)2.
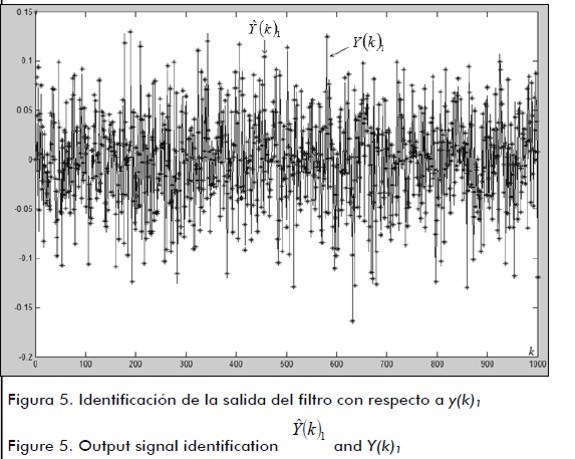
Figures 5 and 6 show identification 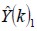 and desired signal Y (k)1 and,
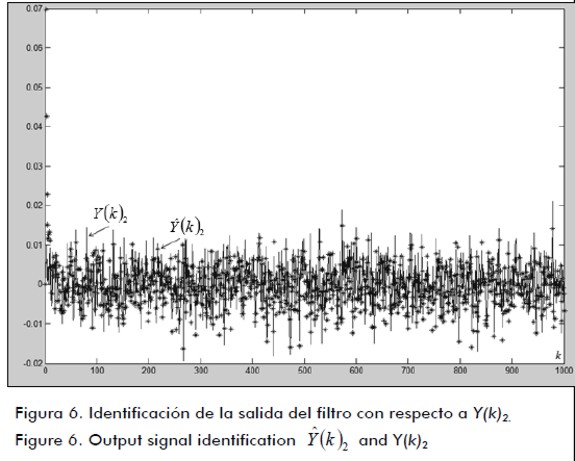
and desired signal Y (k)1 and,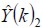 , with Y(k)2 , respectively.
, with Y(k)2 , respectively.
Figures 7 and 8 show the histogram for 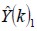 and desired signal Y(k)1 and the histogram for
and desired signal Y(k)1 and the histogram for 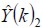 , and Y(k)2, respectively.
, and Y(k)2, respectively.
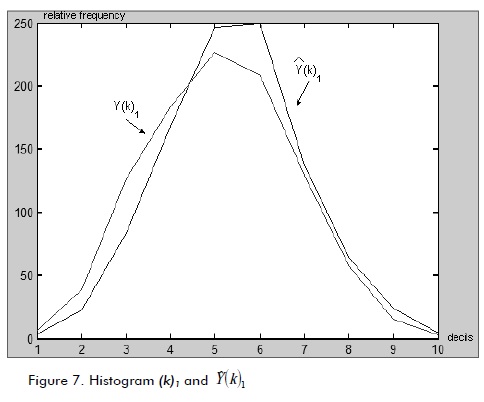
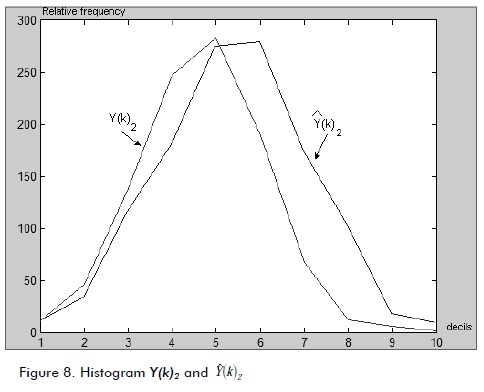
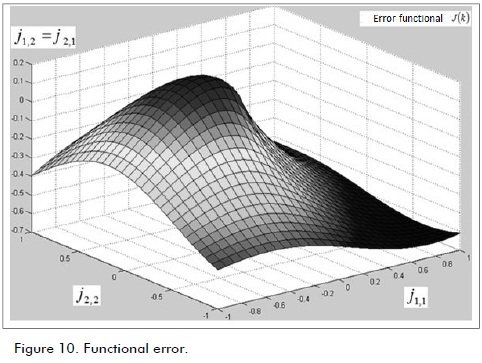
Figure 9 shows the natural error signal described by E(K). Figure 10 shows the minimisation of the natural error signal described as J(K), i.e. the functional error matrix in accordance with Figure 9.
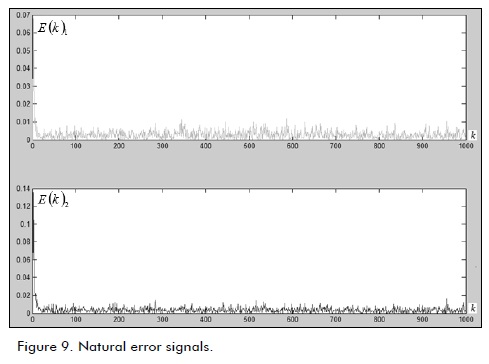
Filter response evolution time was less than the proposed 0.09 sec reference time state change delimited by the processor, considered in (7). Convergence time was 0.0862 sec. which was less than the LDmax evolution time described in (García et al., 2008).
Conclusions
This paper has described a multivariable neural fuzzy digital filter (having multiple inputs and multiple outputs - MIMO) applied to dynamic systems. Its operational adaptive conditions were analysed based on functional error identification and transition matrix within Kalman filter structure in which a back-propagation model integrated into fuzzy mechanisms enabled matrix parameter selection. In simulation, the adaptive inference mechanism classified and deduced filter response in accordance with the desired signal, selecting transition matrix weighting for identification requirements.
Characterising and constructing membership functions from the probabilistic knowledge base as a set of decision rules led to integrating neural network architecture by automatically selecting parameters. The results illustratively described filter output 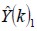 ,
,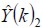 (see Figures 5 and 6). Natural error (see Figure 9)
and functional error J(K)(see Figure 10) showed the convergence levels. Future work will consider evolutionary properties
for estimation instead of fuzzy logic.
(see Figures 5 and 6). Natural error (see Figure 9)
and functional error J(K)(see Figure 10) showed the convergence levels. Future work will consider evolutionary properties
for estimation instead of fuzzy logic.
References
Abraham, K., Fuzzy Expert Systems., Florida, CRC Press, 1991. [ Links ]
Ali, H.S., Fundamentals of Adaptive Filters., New Jersey, John Wiley & Sons, 2003. [ Links ]
Amble, T., Logic Programming and Knowledge Engineering.,USA, Addison Wesley, 1987. [ Links ]
Ash, R., Real Analysis and Probability., USA, Ed. Academic Press, 1970. [ Links ]
García, J.C., Medel, J. J., Guevara, P., RTFDF Description for ARMA Systems., WSEAS Journal: Transactions on Systems and Control, Vol. 2, Issue 10, 2007, pp. 491-496. [ Links ]
García, J.C., Medel, J.J., Guevara, P., Filtrado Digital Difuso en Tiempo Real., Revista Computación y Sistemas, Vol. 11, No. 4, 2008, pp. 390-401. [ Links ]
García, J.C., Medel, J.J., Guevara, P., Real-time neuro-fuzzy digital filtering: Approach., Computer and Simulation in Modern Science, WSEAS press selected papers, Vol. 1, 2008, pp. 122-125. [ Links ]
Haykin, S., Adaptive Filtering., USA, Prentice Hall, 1996. [ Links ]
Huang, G., Zhu, K., Siew, C., Real-Time Learning Capability of Neural Networks., IEEE Transactions on Neural Networks, Vol. 17, 2006, pp. 863-878. [ Links ]
Gustafsson, F., Adaptive Filtering and Change Detection., Inglaterra,John Wiley and Sons, 2000. [ Links ]
Mamdani, E., Applications of Fuzzy Algorithms for Control of Simple Dynamic Plant., Proc. IEEE, Vol. 121, 1974, pp. 1585-1588. [ Links ]
L. Manuel, Teoría de la Medida e Integral de Lebesgue, Universidad Nacional del Rosario, 2003. [ Links ]
Margaliot, M., Langholz, G., New Approaches to Fuzzy Modeling and Control Design and Analysis., Singapore, World Scientific, 2000. [ Links ]
Medel, J.J., Guevara, P., Caracterización de Filtros Digitales en Tiempo-real para Computadoras Digitales., Computación y Sistemas, Vol. VII, No. 3, 2004. [ Links ]
Medel, J.J., García, J.C., Guevara, P., Real-time Fuzzy Digital Filters (RTFDF) Properties for SISO Systems., Automatic Control and Computer Sciences, AVT, Vol. 42, No. 1, 2008, pp. 26-34. [ Links ]
Medel, J.J., García, J.C., Sánchez, J.C., Real-time Neuro-Fuzzy Digital Filtering: Basic Concepts., WSEAS Transactions on Systems and Control, 2008, Vol. 3, Issue 8, pp. 654-663. [ Links ]
Marcek, D., Stock Price Forecasting: Statistical, Classical and Fuzzy Neural Networks., Modeling Decisions for Artificial Intelligence, Springer Verlag, 2004, pp. 41-48. [ Links ]
Morales, G., Introducción a la Lógica Difusa., México, Cinvestav -IPN, 2002. [ Links ]
Nikola, K., Foundations of Neural Networks, Fuzzy Systems, and Knowledge Engineering., Hong Kong, The MIT Press, 1996. [ Links ]
Passino, K.M., Fuzzy Control, USA, Addison Wesley, 1998. [ Links ]
Rajen, B., Gopal, M., Neuro-Fuzzy Decision Trees., International Journal of Neural Filters, Vol. 16, 2006, pp. 63-68. [ Links ]
Shannon, M., A Mathematical Theory of Communication., Bell Systems Technical Journal, Vol.27, 1948, pp. 379-423 and pp. 623-656. [ Links ]
Schneider, M., Kandel, A., Fuzzy expert systems tools., Inglaterra, John Wiley & Sons, 1996. [ Links ]
Takagi, T., Sugeno, M., Fuzzy Identification of Systems and its Applications to Modelling and control., IEEE Transactions and Systems, man, and cybernetics, Vol. 15, 1986, pp. 116-132. [ Links ]
Yamakawa, F., Fuzzy Neurons and Fuzzy Neural Networks., 1989. [ Links ]
Zadeh, L., Fuzzy Sets., Information and control, Vol. 8, 1965, pp. 338-353. [ Links ]











 text in
text in