Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.31 no.1 Bogotá Jan./Apr. 2011
Filtrado digital neuronal difuso: caso MIMO
Neural fuzzy digital filtering: mul- multivariate identifier filters involving tivariate multiple inputs and multiple out-outputs (MIMO) Juan Carlos García Infante1, José de J. Medel Juárez2, Juan Carlos Sánchez García3
1 Ph.D., en Tecnología Avanzada y Ciencia Aplicada en el CICATA Legaria. Vinculado a SEPI, ESIME Culhuacán, México. jcnet21@yahoo.com
2 Ph.D., en ciencias en Control Automático en el CINVESTAV. Vinculado a CIC, México. jjmedelj@yahoo.com.mx
3 Ph.D., en Sistemas Digitales en la UAM Iztapalapa, México. Vinculado a SEPI, ESIME Culhuacán, México. jcsanchezgarcia@gmail.com
RESUMEN
Los filtros identificadores multivariables (MIMO) son sistemas digitales adaptivos que cuentan con retroalimentación para que, de acuerdo a una función objetivo, ajusten su matriz de parámetros con la que se aproximan a la dinámica observable del sistema de referencia. Una forma de que un identificador cumpla con esas condiciones, es la de la lógica difusa por medio de sus mecanismos de inferencia que interpretan y seleccionan en una base de conocimiento la mejor matriz de parámetros. Estos mecanismos de selección mediante las redes neuronales permiten encontrar la respuesta con el mejor nivel de operación para cada cambio de estado (Shannon, 1948). En este artículo se considera en el modelo MIMO del filtrado digital, el proceso neuronal difuso para la estimación matricial de parámetros adaptiva, que se integra en el filtro de Kalman a través de la matriz de transición. Para ello se utilizó la red neuronal del tipo retropropagación en el mecanismo difuso, interpretando sus variables y sus respectivos niveles, seleccionando los mejores valores para ajustar automáticamente los valores de la matriz de transición. La simulación en Matlab presenta al filtrado digital neuronal difuso dando el seguimiento, observándose un funcional de error decreciente exponencialmente.
Palabras clave: filtro digital, control difuso, red neuronal, MIMO, adaptivo.
ABSTRACT
Multivariate identifier filters (multiple inputs and multiple outputs - MIMO) are adaptive digital systems having a loop in accordance with an objective function to adjust matrix parameter convergence to observable reference system dynamics. One way of complying with this condition is to use fuzzy logic inference mechanisms which interpret and select the best matrix parameter from a knowledge base. Such selection mechanisms with neural networks can provide a response from the best operational level for each change in state (Shannon, 1948). This paper considers the MIMO digital filter model using neuro fuzzy digital filtering to find an adaptive parameter matrix which is integrated into the Kalman filter by the transition matrix. The filter uses the neural network as backpropagation into the fuzzy mechanism to do this, interpreting its variables and its respective levels and selecting the best values for automatically adjusting transition matrix values. The Matlab simulation describes the neural fuzzy digital filter giving an approximation of exponential convergence seen in functional error.
Keywords: digital filter, fuzzy control, neural network, MIMO, adaptive digital system.
Recibido: noviembre 25 de 2009. Aceptado: enero 24 de 2011
Introducción
Una red neuronal artificial es un modelo computacional que imita un proceso natural como un sistema biológico, que tiene elementos de procesamiento llamados neuronas, como en el cerebro humano, todas ellas interconectadas, conformando una estructura de red neuronal (Nikola, 1996; Medel et al., 2008). Una red neuronal difusa clasifica, busca y asocia información (Huang, et al., 2006), dando un valor de respuesta correspondiente que esté de acuerdo con la señal deseada del proceso de referencia, construyendo el volumen de control descrito como
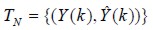
donde 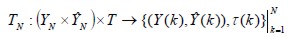 dentro de los
dentro de los
intervalos de membresía delimitados en la base de conocimiento (Schneider y Kandel, 1996).
Filtro neuronal difuso
El conjunto de respuestas dentro de la base de conocimiento representa todas las posibles respuestas correctas del filtro (Gustafsson, 2000; Margaliot y Langholz, 2000; Zadeh, 1965) de acuerdo a una ley objetivo previamente definida por el proceso de referencia natural; el mecanismo de filtrado seleccionará la mejor respuesta de la base de conocimiento en cada estado empleando reglas difusas (if-then).
El filtro neuronal difuso está basado en el algoritmo de retropropagación, ya que sus parámetros se actualizan dinámicamente (Ali, 2003; Amble, 1987; Haykin, 1996) y en diferentes niveles a cada iteración (Huang et al., 2006), en base al error descrito como E(k) (reduciéndolo por medio del criterio 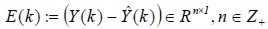 , ésta es la estructura MIMO) que es la diferencia entre la respuesta deseada Y(k) y la salida del filtro actual
, ésta es la estructura MIMO) que es la diferencia entre la respuesta deseada Y(k) y la salida del filtro actual 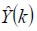 (García et al., 2008; Marcek, 2008). La figura 1 muestra el proceso del filtrado (Passino, 1998):
(García et al., 2008; Marcek, 2008). La figura 1 muestra el proceso del filtrado (Passino, 1998):
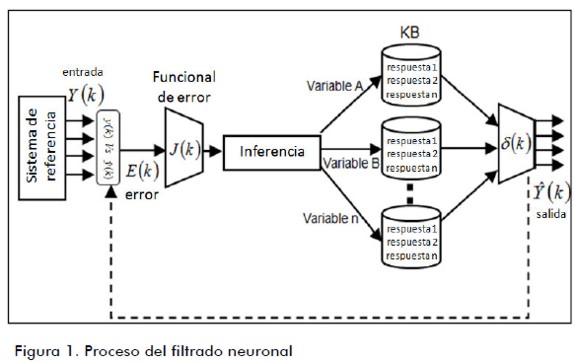
El error (E(k)) está limitado en el intervalo [0, ε] y ε es descrito como un valor positivo de acuerdo con 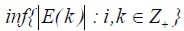 donde i es el índice, con k intervalos (Margaliot y Langholz, 2000; Morales, 2002). Descrito de la forma: sup
donde i es el índice, con k intervalos (Margaliot y Langholz, 2000; Morales, 2002). Descrito de la forma: sup 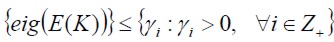 , t a l q u e
, t a l q u e 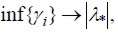 , donde ,
, donde , 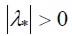 , sup
, sup 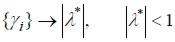
El filtro neuronal difuso está basado en los siguientes elementos, considerando los conceptos descritos en (Abraham, 1991; Ali, 2003; Gustafsson, 2000; Mamdani, 1974; Morales, 2002):
Entrada de inferencia difusa: en esta etapa la señal deseada Y(k) desde el sistema de referencia a la entrada del filtro tiene una descripción en un sentido métrico (Ash, 1970).
Base de reglas: son intervalos de rango dinámico que hacen una interpretación o inferencia en la entrada del filtro empleando el conector lógico binario conocido como Si (IF).
Mecanismo de inferencia: es la acción experta con respecto a la base de reglas, conocida como consecuencia para seleccionar la función de membresía correspondiente descrita como Â(K) por medio del conector lógico binario Entonces (THEN) (Yamakawa, 1989).
Función de activación: ésta es la etapa de filtrado, la cual es la respuesta digital del filtro transformada en una respuesta natural. Es el valor que tiene la mejor aproximación a la señal deseada, sustentada en una base de conocimiento definida previamente.
Realimentación natural: finalmente, el proceso de filtrado toma el valor lingüístico correcto y actualiza los parámetros del filtro a una condición natural con respecto al sistema de referencia, considerando la diferencia de error existente entre Y(K) y 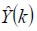 de forma dinámica, utilizando el criterio descrito como funcional de error (es la matriz del funcional del error J(K) que describe la relación de convergencia entre el valor observado real y su estimación. En forma recursiva es:
de forma dinámica, utilizando el criterio descrito como funcional de error (es la matriz del funcional del error J(K) que describe la relación de convergencia entre el valor observado real y su estimación. En forma recursiva es: 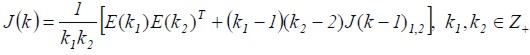 .)
.)
El funcional de error es una matriz cuadrática dimensional donde, 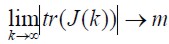 es la matriz de referencia y el sistema es convergente a m si
es la matriz de referencia y el sistema es convergente a m si 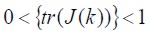 . El funcional es expresado con respecto al segundo momento de probabilidad, teniendo un valor ínfimo descrito en (1 ).
. El funcional es expresado con respecto al segundo momento de probabilidad, teniendo un valor ínfimo descrito en (1 ).
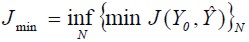 | (1) |
En resumen el filtrado neuronal difuso tiene previamente toda la información requerida dentro de su base de conocimiento para seleccionar la respuesta correspondiente al valor de la señal deseada en la entrada del filtro. Primero, el proceso de filtrado emplea las reglas difusas establecidas para hacer una inferencia o interpretación del vector de la señal deseada expresada como Y(K) (Takagi y Sugeno, 1986). El mecanismo del filtro selecciona dentro de su estructura de datos la variable activada y su nivel correspondiente (la variable, por ejemplo, puede ser A: temperatura, B: velocidad y C: presión, y su respectivo nivel: bajo, medio y alto); entonces el mecanismo de reglas selecciona el parámetro correspondiente Â(K) para ajustar el filtro y dar el vector de respuesta correcto 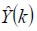 a la entrada del filtro (Rajem y Gopal, 2006).
a la entrada del filtro (Rajem y Gopal, 2006).
Propiedades de la matriz de parámetros
Para hacer la descripción de un filtro neuronal difuso en su forma multivariable con variaciones de tiempo, el parámetro 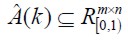 debe cumplir condiciones de acuerdo a la matriz de transición:
debe cumplir condiciones de acuerdo a la matriz de transición:
Tiene restricciones en su operación de acuerdo a las propiedades dinámicas de la matriz de transición: 1)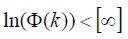 , 2)
, 2)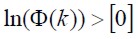 ,3)
,3)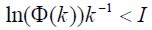 . Donde ,
. Donde , 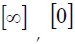 y I son las matrices descritas como infinito, nula y la identidad de forma respectiva. El estimador por medio de la matriz de transición es descrito en (2).
y I son las matrices descritas como infinito, nula y la identidad de forma respectiva. El estimador por medio de la matriz de transición es descrito en (2).
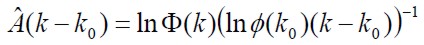 | (2) |
Cuyas velocidades de cambio están acotadas dentro de la función de transición (3 ).
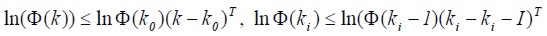 | (3) |
La matriz de transición se encuentra acotada en 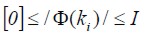 .
.
De acuerdo al valor del 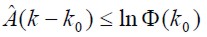 , la matriz de parámetros estimada cumple con la desigualdad (4).
, la matriz de parámetros estimada cumple con la desigualdad (4).
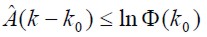 | (4) |
Y el identificador de Kalman usando a (4), se presenta en (5).
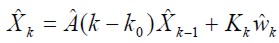 | (5) |
Donde 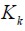 es la matriz de ganancias de Kalman descrita por la varianza del error de identificación definido por la diferencia de la señal deseada respecto de la señal de salida del filtro, descrito de manera recursiva,y
es la matriz de ganancias de Kalman descrita por la varianza del error de identificación definido por la diferencia de la señal deseada respecto de la señal de salida del filtro, descrito de manera recursiva,y 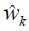 es el ruido que excita al proceso de referencia.
es el ruido que excita al proceso de referencia.
Resultados
La simulación del filtro neural difuso MIMO se realiza considerando al filtro de Kalman (Haykin, 1996) con una matriz de transición descrita por la base del conocimiento de acuerdo al criterio del funcional del error (Ash, 1970). Los tiempos de evolución que delimitan un sistema de tipo soft (estadístico) implantado en una computadora con procesador AMD Sempron 3100+ con intervalos k, teniendo un promedio en el tiempo de evolución de 0,004 seg ± 0,0002 seg. El sistema ARMA básicamente representa un sistema de referencia en un espacio de estados discreto expresado por la diferencia de primer orden en (6).
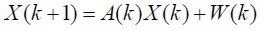 | (6) |
Y su salida es descrita en (7).
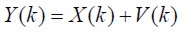 | (7) |
Donde 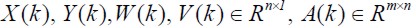
X(k) es el vector de estados internos, A(k) es la matriz de parámetros, W(k) es el conjunto de ruidos que perturban al sistema, y(k) es el conjunto de vectores de señales deseadas del sistema de referencia a la entrada del filtro y V(k) es el vector de ruidos de salida. Los diferentes niveles de operación están descritos para operar con respecto al funcional del error1. El proceso de filtrado establece para cada variable una descripción lingüística expresada por los niveles: bajo, medio y alto. La figura 2 muestra la estimación de la matriz de parámetros descrita en este caso por una matriz 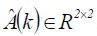
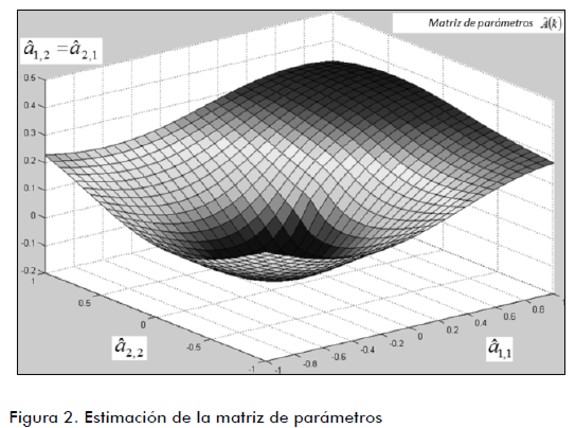
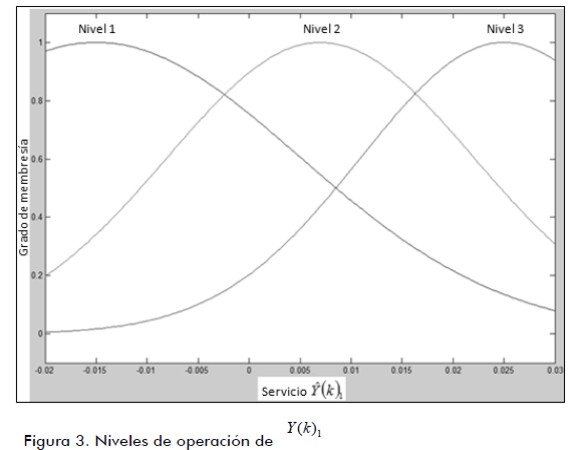
De acuerdo a la estimación de parámetros descrita con la variable Â(K), la figura 3 muestra la proyección de los niveles de respuesta a la salida del filtro descrita con la variable 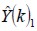 respecto de la señal deseada del sistema de referencia Y(k)1. En cuanto a los valores de Â(K), la figura 4 muestra la proyección de los niveles a la salida del filtro con respecto a la variable
respecto de la señal deseada del sistema de referencia Y(k)1. En cuanto a los valores de Â(K), la figura 4 muestra la proyección de los niveles a la salida del filtro con respecto a la variable 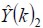 y a la señal deseada del sistema de referencia descrita como Y(k)2 .
y a la señal deseada del sistema de referencia descrita como Y(k)2 .
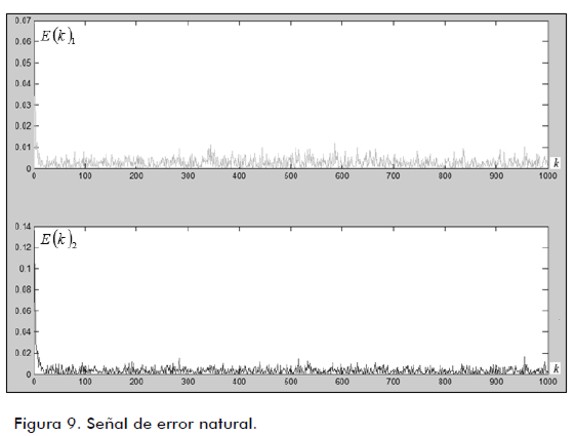
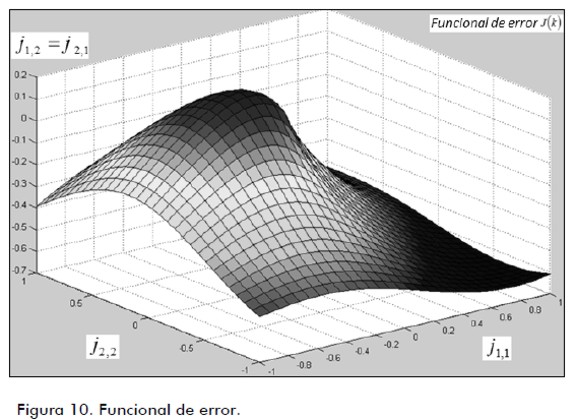
La figura 5 muestra la estimación de La figura 7 exhibe el histograma de La figura 9 revela la señal de error natural descrita como E(K) de acuerdo a cada señal deseada y la diferencia con la señal de salida respectiva; y la figura10, la minimización de la señal de error natural descrita como J(K) que es la matriz del funcional del error de acuerdo a la figura 9. Según el análisis de los resultados, el tiempo de evolución de la respuesta del filtro es menor que el tiempo de cambio de estado del proceso de referencia propuesto con el valor 0,09 seg, delimitado por el procesador, de acuerdo a la condición descrita en (7). El tiempo de convergencia es de 0,0862 seg, el cual es menor que la condición de tiempo de evolución de la referencia descrito como LDmax (García et al., 2008), de acuerdo a las propiedades descritas en las definiciones de este trabajo. Conclusiones En el artículo se describe al filtrado digital neural difuso multivariable (MIMO Multiple Inputs and Multiple Outputs), aplicado a sistemas dinámicos. Se realiza un análisis de su operación como un filtro adaptivo en función del error de identificación por medio de la matriz de transición dentro del filtro de Kalman. Para la selección adaptiva de la matriz de parámetros se consideró como herramienta el proceso formado por la red neuronal de retropropagación con los mecanismos difusos de selección de la matriz de parámetros, describiendo con la simulación el mecanismo de inferencia adaptiva, el cual clasifica y deduce las respuestas del filtro de acuerdo a la señal deseada y basada en el criterio de error, para seleccionar los valores de los pesos de la matriz de transición dentro del filtro identificador. Se establece cómo construir y caracterizar las funciones de membresía de la base de conocimiento descrita en forma probabilística con el conjunto de reglas de decisión, integrando la arquitectura de la red neuronal de retropropagación para la selección automática de los parámetros de la matriz de transición. Los resultados se mostraron de forma ilustrativa, describiendo a la salida del filtro como Referencias Abraham, K., Fuzzy Expert Systems., Florida, CRC Press, 1991. [ Links ] Ali, H.S., Fundamentals of Adaptive Filters., New Jersey, John Wiley & Sons, 2003. [ Links ] Amble, T., Logic Programming and Knowledge Engineering.,USA, Addison Wesley, 1987. [ Links ] Ash, R., Real Analysis and Probability., USA, Ed. Academic Press, 1970. [ Links ] García, J.C., Medel, J. J., Guevara, P., RTFDF Description for ARMA Systems., WSEAS Journal: Transactions on Systems and Control, Vol. 2, Issue 10, 2007, pp. 491-496. [ Links ] García, J.C., Medel, J.J., Guevara, P., Filtrado Digital Difuso en Tiempo Real., Revista Computación y Sistemas, Vol. 11, No. 4, 2008, pp. 390-401. [ Links ] García, J.C., Medel, J.J., Guevara, P., Real-time neuro-fuzzy digital filtering: Approach., Computer and Simulation in Modern Science, WSEAS press selected papers, Vol. 1, 2008, pp. 122-125. [ Links ] Haykin, S., Adaptive Filtering., USA, Prentice Hall, 1996. [ Links ] Huang, G., Zhu, K., Siew, C., Real-Time Learning Capability of Neural Networks., IEEE Transactions on Neural Networks, Vol. 17, 2006, pp. 863-878. [ Links ] Gustafsson, F., Adaptive Filtering and Change Detection., Inglaterra,John Wiley and Sons, 2000. [ Links ] Mamdani, E., Applications of Fuzzy Algorithms for Control of Simple Dynamic Plant., Proc. IEEE, Vol. 121, 1974, pp. 1585-1588. [ Links ] L. Manuel, Teoría de la Medida e Integral de Lebesgue, Universidad Nacional del Rosario, 2003. [ Links ] Margaliot, M., Langholz, G., New Approaches to Fuzzy Modeling and Control Design and Analysis., Singapore, World Scientific, 2000. [ Links ] Medel, J.J., Guevara, P., Caracterización de Filtros Digitales en Tiempo-real para Computadoras Digitales., Computación y Sistemas, Vol. VII, No. 3, 2004. [ Links ] Medel, J.J., García, J.C., Guevara, P., Real-time Fuzzy Digital Filters (RTFDF) Properties for SISO Systems., Automatic Control and Computer Sciences, AVT, Vol. 42, No. 1, 2008, pp. 26-34. [ Links ] Medel, J.J., García, J.C., Sánchez, J.C., Real-time Neuro-Fuzzy Digital Filtering: Basic Concepts., WSEAS Transactions on Systems and Control, 2008, Vol. 3, Issue 8, pp. 654-663. [ Links ] Marcek, D., Stock Price Forecasting: Statistical, Classical and Fuzzy Neural Networks., Modeling Decisions for Artificial Intelligence, Springer Verlag, 2004, pp. 41-48. [ Links ] Morales, G., Introducción a la Lógica Difusa., México, Cinvestav -IPN, 2002. [ Links ] Nikola, K., Foundations of Neural Networks, Fuzzy Systems, and Knowledge Engineering., Hong Kong, The MIT Press, 1996. [ Links ] Passino, K.M., Fuzzy Control, USA, Addison Wesley, 1998. [ Links ] Rajen, B., Gopal, M., Neuro-Fuzzy Decision Trees., International Journal of Neural Filters, Vol. 16, 2006, pp. 63-68. [ Links ] Shannon, M., A Mathematical Theory of Communication., Bell Systems Technical Journal, Vol.27, 1948, pp. 379-423 and pp. 623-656. [ Links ] Schneider, M., Kandel, A., Fuzzy expert systems tools., Inglaterra, John Wiley & Sons, 1996. [ Links ] Takagi, T., Sugeno, M., Fuzzy Identification of Systems and its Applications to Modelling and control., IEEE Transactions and Systems, man, and cybernetics, Vol. 15, 1986, pp. 116-132. [ Links ] Yamakawa, F., Fuzzy Neurons and Fuzzy Neural Networks., 1989. [ Links ] Zadeh, L., Fuzzy Sets., Information and control, Vol. 8, 1965, pp. 338-353. [ Links ]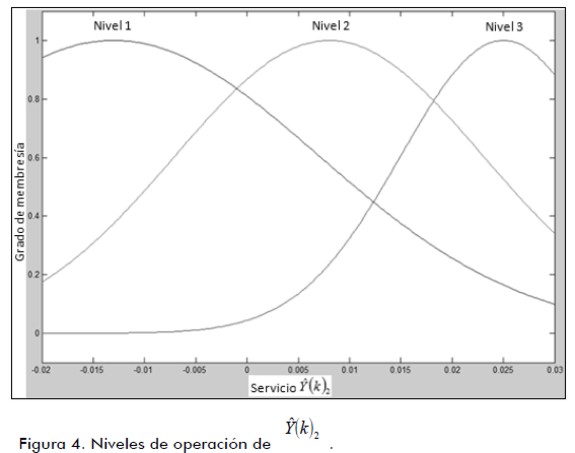
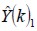 , con respecto a la señal deseada Y(k)1 a la entrada del filtro, y la figura 6 la estimación de
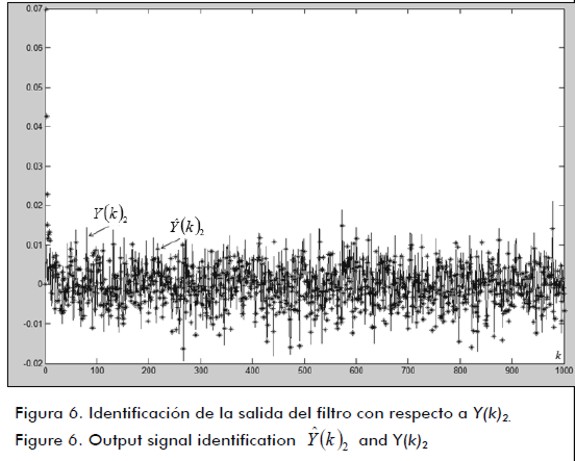
, con respecto a la señal deseada Y(k)1 a la entrada del filtro, y la figura 6 la estimación de 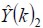 , con respecto a la señal deseada Y(k)2 a la entrada del filtro.
, con respecto a la señal deseada Y(k)2 a la entrada del filtro.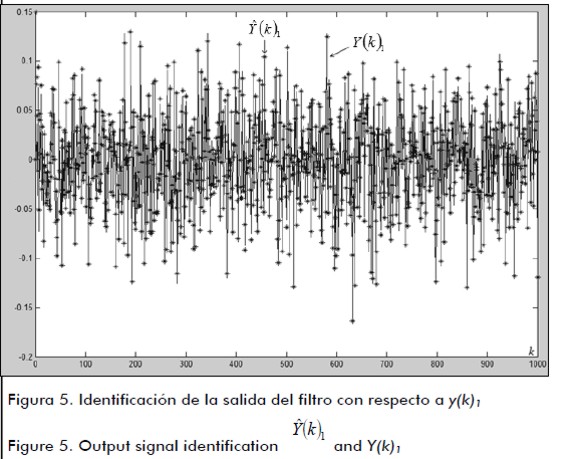
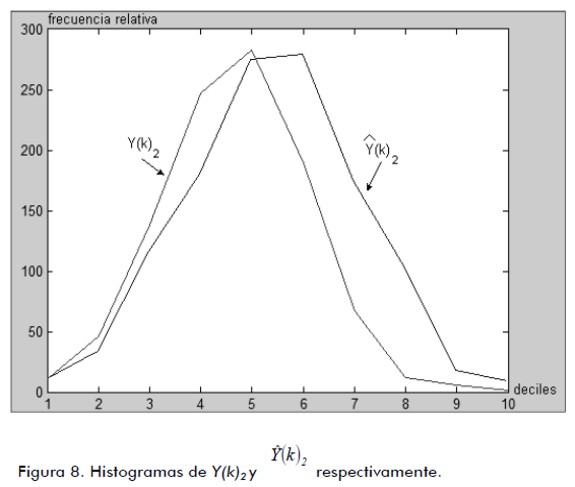
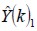 , y de la señal deseada Y(k)1 y la figura 8 el histograma de
, y de la señal deseada Y(k)1 y la figura 8 el histograma de 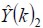 , y de la señal deseada Y(k)2 .
, y de la señal deseada Y(k)2 .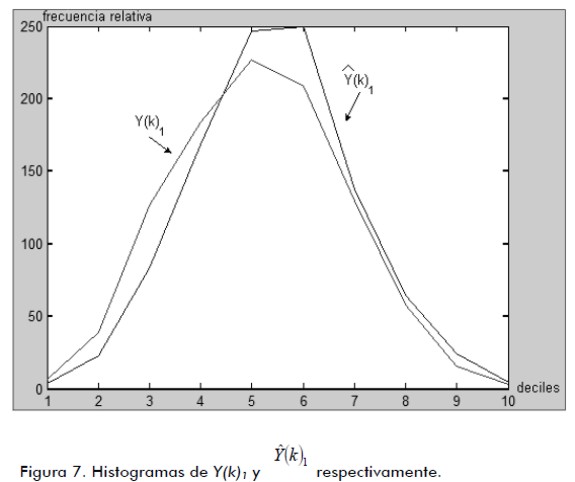
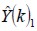 con respecto a la señal deseada expresada como Y(K)1 como se ve en la figura 5, así como
con respecto a la señal deseada expresada como Y(K)1 como se ve en la figura 5, así como 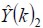 y en la figura 6 , minimizando el error natural (figura 9) y el funcional del error J(K) (figura 10). Como trabajo futuro se necesita ver el proceso de estimación con un sistema evolutivo, y comparar sus con los actuales.
y en la figura 6 , minimizando el error natural (figura 9) y el funcional del error J(K) (figura 10). Como trabajo futuro se necesita ver el proceso de estimación con un sistema evolutivo, y comparar sus con los actuales.











 text in
text in 


