Elkin Florez¹, Yamid Carranza², Yesid Ortiz³

¹ Ingeniero Mecánico, Universidad Francisco de Paula Santander, Colombia. Magíster en Ingeniería Mecánica, Universidad de los Andes, Colombia. Magíster en Ingeniería Química y de Procesos, Universidad de Rovira i Virgili, España. Doctor en Ingeniería Mecánica, Aeronáutica y de Fluidos. Universidad Politécnica de Cataluña, España. Profesor asociado, Universidad de Pamplona. eflorez@unipamplona.edu.co

² Ingeniero Mecánico, Universidad Tecnológica de Pereira, Colombia. Magister en Ingeniería Mecánica , Universidad de los Andes, Colombia. Estudiante de doctorado, Politécnico de Monterrey, México. Profesor Asistente, Universidad Tecnológica de Pereira, Colombia. yamidc@utp.edu.co

³ Ingeniero Mecánico, Universidad Francisco de Paula Santander, Colombia. Magíster en Ingeniería Mecánica, Universidad de los Andes, Colombia. Profesor Asistente, Universidad Tecnológica de Pereira, Colombia. yosanchez@utp.edu.co

RESUMEN

Se presenta una solución numérica del flujo sobre un escalón en dos dimensiones utilizando el método de la ecuación reticular de Boltzmann (LBEM). A diferencia de los métodos numéricos tradicionales basados en la discretización de las ecuaciones macroscópicas del continuo (conservación de la masa y Navier-Stokes), los LBEM se fundamentan en modelos microscópicos y mesoscópicos de las ecuaciones cinéticas. Se muestran los resultados obtenidos para este flujo en el estado estacionario y para un amplio rango de números de Reynolds (100 ≤ Re ≤ 1000), y se han comparado con estudios previos. Se ha investigado la aparición y localización de los principales vórtices en el flujo, tanto en la pared inferior como en la superior, y su comportamiento en función del número de Re. Se han implementado al modelo LBEM dos tipos comunes de condiciones de frontera: condición de Drichlet a la entrada (perfil de velocidad parabólico) y condición de Newman a la salida (derivada nula de la velocidad). Los resultados obtenidos muestran gran exactitud del método utilizado para un amplio rango de números de Reynolds, al ser comparados con resultados experimentales y numéricos de otros autores.

Palabras clave: flujo de fluidos, método de la ecuación reticular de Boltzmann, simulación numérica

ABSTRACT

Numerical solutions of 2-D laminar flow over a backwardfacing step using the lattice Boltzmann equation method (LBEM) are presented in this article. Unlike conventional numerical schemes based on macroscopic continuum equation (mass conservation and Navier-Stokes) discretisation, the LBEM is based on microscopic models and mesoscopic kinetic equations. The simulations were validated for a wide range of Reynolds numbers (100 ≤ Re ≤ 1,000), comparing them to previous studies. Several flow features, such as primary and secondary vortex location at the bottom and top of the wall, respectively, were investigated regarding Reynolds number. Two typical classes of boundary condition were implemented in the LBEM model: the Drichlet condition at the inlet flow (parabolic speed profile) and the Newman condition at the outlet flow (zero gradient speed). The results showed that the LBEM gave accurate results over a wide range of Reynolds number; these were compared with other numerical methods and experimental data.

Keywords: fluid flow, lattice Boltzmann equation method, numerical simulation.

Recibido: febrero 16 de 2010

Aceptado: mayo 25 de 2011

Introducción

Los flujos por canales donde existe separación y recirculación de la capa límite se encuentran con frecuencia en muchos problemas de flujos en ingeniería. Ejemplos típicos son los flujos en un intercambiador de calor y en ductos. Entre estos tipos de problemas, el flujo sobre un escalón puede ser considerado como la más sencilla geometría con un rico contenido físico que se pone de manifiesto en los vórtices que se presentan y sus respectivas recirculaciones, todas éstas dependiendo del número de Reynolds (Re) y del parámetro que relaciona la altura del escalón con la altura del canal.

En la literatura es posible encontrar muchos estudios numéricos de un flujo 2D incompresible y estable para el flujo alrededor de un escalón en un canal (BFS). En estos estudios se puede determinar una controversia sobre si es posible o no obtener una solución estable para un Re ≥ 800. Este hecho ha sido discutido en detalle (Gresho et al.,1993), donde se concluyó que el flujo sobre un escalón es estable y computable a Re = 800. Otros autores (Keskar y Lyn, 1999; Barton, 1997; Sheu y Tsai, 1999; Biagioli, 1998; Erturk, 2008) han presentado soluciones del flujo BFS por encima de Re = 800, utilizando diversos métodos de discretización de las tradicionales ecuaciones de Navier-Stokes.

No es necesario mencionar que los LBEM están en desarrollo a un alto ritmo y se han convertido en un poderoso método para la simulación de flujos de fluido (Moahamad y Kuzmin, 2010). Sin embargo, hay aún muchas temáticas que necesitan más investigaciones y evaluaciones críticas. Además, el método no es muy utilizado por algunos autores debido a las limitaciones y restricciones que generan los parámetros inherentes en los LBEM. Algunos de éstos son: el tratamiento adecuado de las condiciones de frontera, condiciones iníciales, y el tiempo de relajación, que son los temas estudiados en este trabajo.

Los LBEM están definidos como un esquema en diferencias finitas y tiempo explícito de la ecuación de Boltzmann continua en el espacio de fase y tiempo (He y Luo, 1997). Los LBEM cuentan con una retícula cartesiana en el espacio, a consecuencia de la simetría del conjunto de la velocidad discreta y el hecho de que el espaciado reticular Dx está relacionado con el paso de tiempo Δt por Δx Δt = c, donde c es la unidad base de la velocidad discreta. Esto hace de los LBEM un esquema muy simple que consiste en dos pasos esenciales: la colisión y la advección. Los modelos de colisión hacen referencia a las diversas interacciones entre las partículas del fluido y la advección simplemente traslada las partículas desde una celda de la red a otra vecina de acuerdo con sus velocidades. La simplicidad y la naturaleza cinética de los LBEM son unas de las características que los hacen atractivos.

El método de la ecuación reticular de Boltzmann se basa en la idea original de los autómatas celulares de gases en redes (Frisch, 1986). Para simular el movimiento del fluido dentro de la retícula se utiliza un esquema mesoscópico, donde el paso del tiempo es unitario y existe una fase-espacio discreta. En el dominio reticular cada celda representa un elemento volumen del fluido, y este elemento de volumen consiste de un grupo de partículas para las cuales su movimiento está especificado por una función de distribución de partículas (fdp). En el modelo clásico la fdp es la distribución de Maxwell-Boltzmann. En cada paso de tiempo las partículas se mueven, de acuerdo al modelo seleccionado, hacia las celdas adyacentes (paso de propagación) y colisionan con otras partículas que vienen o viajan hacia la misma celda en diferentes direcciones (paso de colisión). Las variables macroscópicas como la densidad y la velocidad son calculadas a partir de las fdp (Maxwell, 1997; Dieter, 2000).

Con el fin de conocer la eficacia del LBEM, en el presente trabajo se ha resuelto numéricamente el flujo sobre un escalón para números de Reynolds de 100 ≤ Re ≤ 1000, y se ha determinado la exactitud del método, comparando y haciendo una breve discusión con los datos, tanto numéricos como experimentales, obtenidos por otros autores.

Metodología

El principio que guía los LBEM es la construcción de un sistema dinámico en una retícula simple y simétrica (en su mayoría cuadrados en 2D y en 3D cúbicos) el cual involucra una serie de cantidades que pueden ser interpretadas como la pdf de partículas ficticias sobre los vínculos de la retícula. Estas cantidades luego evolucionan en un tiempo discreto según ciertas reglas que se seleccionan para lograr un comportamiento macroscópico deseable que surge con relación a las grandes escalas con el espaciado reticular (Lalleman y Luo, 2000). La ecuación reticular de Boltzmann está dada por (He y Luo, 1997; Dieter, 2000; Succi, 2001):

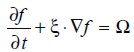[1]

donde Ω es la función de colisión, término que puede simplificarse bastante utilizando la aproximación de Bhatnagar-Gross-Krook (BGK), con un solo tiempo de relajación τ (SRT), el método más sencillo utilizado para resolver la ecuación (1 ). éste consiste en reemplazar el término de colisión por un término que relaciona la diferencia entre la función f y la función de equilibrio de Maxwell-Boltzmann, y un tiempo de relajación.

El argumento básico para el uso de estos tipos de métodos cinéticos simplificados en la simulación de flujos de fluidos macroscópicos es el de que la dinámica macroscópica de un fluido es el resultado de la conducta colectiva de muchas partículas microscópicas en el sistema y que la dinámica macroscópica no es sensible a los detalles subyacentes en la física microscópica. Mediante el desarrollo de una versión simplificada de las ecuaciones cinéticas complejas, como lo es la ecuación de Boltzmann, es posible evitar que sigue a cada partícula como en simulaciones de dinámica molecular (Chen y Doolen, 1998). El LBEM se puede escribir como

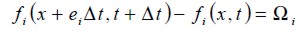[2]

Donde f_i(x,∪,t), son las funciones de distribución de las partículas, con x y ∪ como la posición y la velocidad de la partícula, respectivamente, sobre el espacio fase (x, ∪) y tiempo t. Aquí las cantidades macroscópicas, como la velocidad y la densidad, se pueden obtener a partir de los momentos de f (x,∪,t). El operador de colisión Ω del lado derecho de la ecuación (2) utilizando la aproximación BGK puede ser reemplazado por (Dieter, 2000):

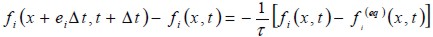[3]

donde fi^(eq)(x,t) es la función de distribución de equilibrio, ei son los vectores de velocidades discretas y Τ; es el tiempo de relajación, el cual está relacionado con la viscosidad cinética del fluido mediante (He y Luo, 1997):

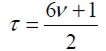[4]

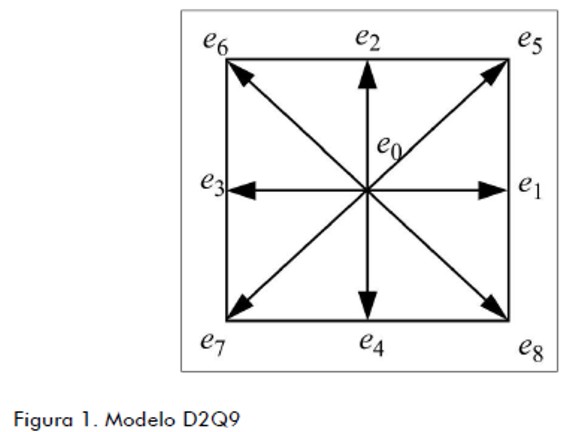
La figura 1 muestra el modelo estándar D2Q9 (bidimensional y nueva velocidades discretas) de la celda utilizada en el presente trabajo, donde la función de distribución de equilibrio para flujos isotérmicos y estables está definida por (Quian, 1992):

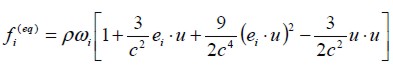[5]

donde ρ y u son la velocidad macroscópica y la densidad, respectivamente, y ω_i son los factores de peso constantes, que para el modelo D2Q9 están dados por:

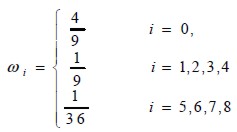[6]

Las velocidades discretas, ei, para el modelo D2Q9 (figura 1) están definidas como sigue:

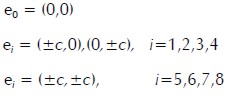donde c=Δx/Δt=Δy/Δt, Δx y Δt son el espacio de la celda y el paso de tiempo, respectivamente, que son un unitarios. Las cantidades hidrodinámicas básicas se obtienen mediante la sumatoria de los momentos en el espacio-velocidad.

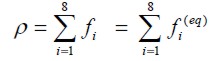[7]

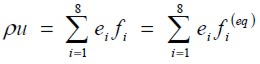[8]

La viscosidad macroscópica se obtiene a partir de:

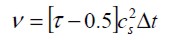[9]

donde c_s el la velocidad del sonido e igual a c/Ö3 (Mohamad et al., 2010).

La evolución del sistema para el modelo BGK está determinada por dos pasos principales: propagación (movimiento hacia las celdas vecinas) y colisión (redistribución de las f’^s de cada celda), calculados mediante:

Collision step:

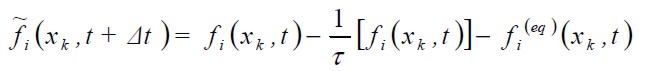[10]

Streaming step:

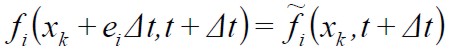donde ƒⁱ, representa el paso de poscolisión. Este paso es totalmente local, y el de propagación no exige grandes prestaciones computacionales (Quian, 1992; Maxwell, 1997).

Modelo del flujo por medio de un escalón

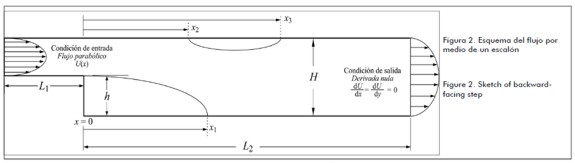
En la figura 2 se muestra el esquema del flujo considerado. En este estudio la entrada del flujo está ubicada aguas arriba del escalón y se localiza a una distancia L₁ = 4h detrás del escalón y la salida ubicada a una distancia L₂ = 35h El número de nodos en la dirección horizontal es N_x = (L₁ + L₂). La longitud del canal a la salida se seleccionó teniendo en cuenta que los puntos de recirculación del flujo no sean afectados por la misma condición de salida del flujo. La altura del canal utilizada es de H = 2h.= N_y-2, donde N_y es el número de nodos en la dirección vertical del canal. La malla utilizada o retícula es totalmente uniforme en todo el dominio. La distancia x1 determina el punto donde se presenta la recirculación del flujo en la pared inferior y las distancias x₂ y x₃ definen los puntos de recirculación en la pared superior. Todas las distancias son referenciadas al escalón, en x=0 según la figura (2).

Condiciones a la entrada del flujo

Barton (1997) estudió el efecto de la longitud del canal antes del escalón (entrada del flujo) y demostró que las soluciones que se obtienen del flujo sólo son afectadas para bajos números de Reynolds. En esta investigación la longitud de la entrada del canal, antes del escalón, fue seleccionada igual a; L₁ = 4h. La condición impuesta es la de un flujo totalmente desarrollado tal como un flujo de Poiseuille entre dos placas planas, que equivale a la imposición de un perfil parabólico para la velocidad (U = u_x, u_y = 0). Las funciones de distribución ( f_i ) desconocidas en los nodos de la entrada son calculadas utilizando las f’s que arriban a éstos desde el interior del dominio y el valor correspondiente de la velocidad en cada nodo. Para el modelo D2Q9, y tomando como ejemplo el nodo x_A que muestra la figura 3, después del paso de propagación la f₀ f₂, f₃, f₄, f₆, y la f₇ son conocidas, debido a que arriban de los nodos siguientes a x_A, y las funciones f₁, f₅, y f₈ se calculan utilizando las ecuaciones (7) y (8) y la condición de igualdad para la función de distribución de no equilibrio en la dirección normal a la entrada del flujo. éstas se determinan de la siguiente forma:

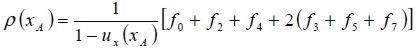[11]

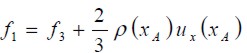[12]

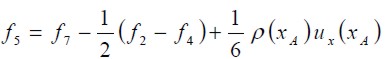[13]

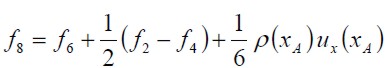[14]

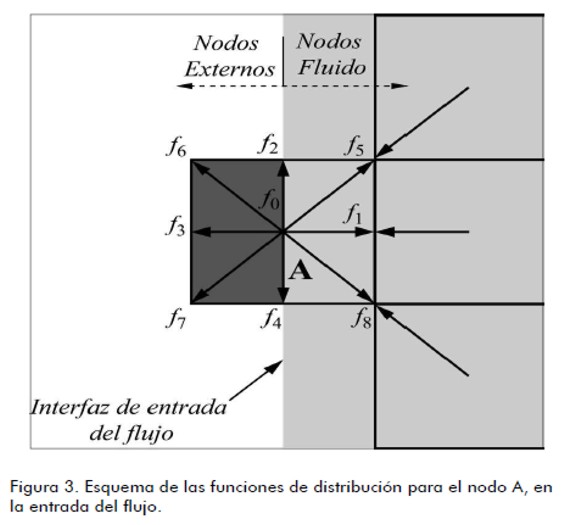
Un paso de colisión es necesario a los fines de obtener 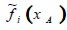para i = 1,5 y 8. Tanto en la esquina superior como en la inferior el cálculo de las f ’s desconocidas requiere un tratamiento especial para evitar la pérdida de partículas.

Condiciones a la salida del flujo

Aquí se comprobaron dos tipos de condiciones. Primero se implementó la misma condición que a la entrada (condición de Drichlet) imponiendo un perfil parabólico de velocidad, con la diferencia de que a la salida, las f ’s a calcular son f₃, f₆ y f₇. También, se implementó la condición de derivada nula para la velocidad (condición de Newman), donde el valor de la velocidad en el nodo perteneciente a la salida tiene el mismo valor que el nodo inmediatamente anterior en la dirección x. Estas condiciones han demostrado no afectar considerablemente el flujo (Zou y He, 1997; Bouzide et al., 2001; Latt, 2008).

Condiciones de pared fija

Para tratar el paso de propagación en presencia de fronteras de pared fija se utiliza la aproximación lineal propuesta por Bouzidi (2001), conocida como Bounce-back, en la que se ubica la pared en la mitad del camino entre el nodo sólido y el nodo fluido. Suponiendo que rl es un nodo fluido tal que r_l + e_i es un nodo sólido, y llamando a e_{i ’} la velocidad invertida o de dirección inversa de e_i (e_{i ’} = -e_i), se tiene que

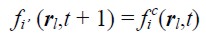[15]

En el lado derecho de la ecuación (15), la f c es tomada después de la colisión y antes de la propagación. La f ( ·¸ t + 1) del lado izquierdo de la ecuación se usaría en valores después de la colisión y de la propagación, la cual corresponde a un paso de tiempo LBM completo. Lo anterior indica que la dinámica de los nodos sólidos y los nodos fluido, vecinos de la pared, difieren únicamente en el paso de propagación (Flórez, 2008).

Resultados y discussion

El diagrama de flujo utilizado para el desarrollo del código computacional con el cual se obtuvieron los resultados es el propuesto por Flórez (2008). El lenguaje de programación utilizado es Fortran 90. Los valores definidos en unidades reticulares según Latt (2008), fueron seleccionados teniendo en cuenta la teoría existente y las restricciones del método, éstos son: tiempo de relajación τ = 0,54, velocidad máxima a la entrada del canal U_max = 0,057, el número de Reynolds, Re = 2h·U_max/3v, donde v es obtenida de la ecuación (3), el número de nodos utilizados N_x y N_y son función del Re a simular. Los respectivos valores son: Re = 100 N_x = 850, N_y = 52, Re = 200 N_x = 1.700, N_y = 102, Re = 300 N_x = 2.550, N_y = 152, Re = 400 N_x = 2.550, N_y = 152 y, para Re > 500 N_x = 4.250, N_y = 252.

Como se muestra en la ecuación (16), donde r define la coordenada del nodo y t el paso del tiempo, la velocidad promedio calculada mediante todo el dominio fue el criterio de convergencia utilizado en todas las simulaciones. Buscando una gran exactitud en los resultados la tolerancia utilizada estuvo definida por tol = 10 ^-7.

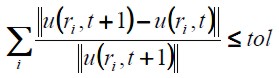[16]

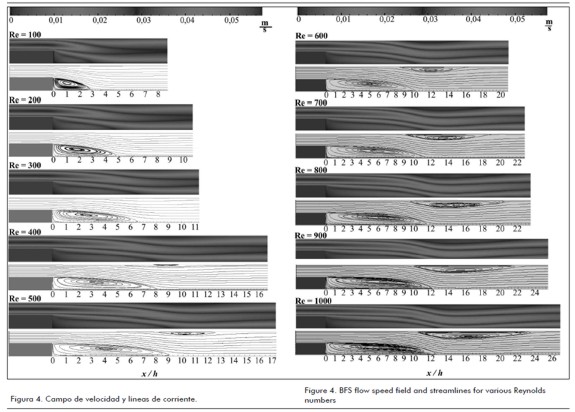
La figura 4 muestra los campos de velocidad y las respectivas líneas de corriente del flujo por medio de un escalón para 100 ≤ Re ≤ 1.000. En los campos de velocidad se puede ver cómo se distribuye la magnitud de la velocidad dentro del canal a medida que el número de Re se incrementa. Las líneas de corriente exhiben la formación de las regiones de recirculación. Es de notar que en esta figura la escala en la dirección x e y se ha manipulado para poder observar con claridad la diferencia en los detalles para todo el rango de números de Re. Y es importante mencionar que las líneas de corriente permiten observar de forma clara la aparición de la recirculación en la pared superior para Re ≥ 400. En todo el rango de números de Re, 100 ≤ Re ≤ 1.000 los resultados han sido comparados con los obtenidos numérica y experimentalmente por otros autores. En la mayoría de los casos este flujo ha sido investigado hasta un Re de 800.

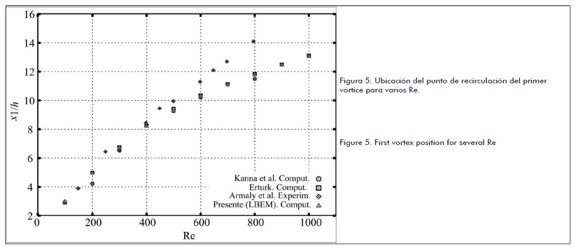
La figura 5 muestra el punto de recirculación del primer vórtice sobre la pared inferior del canal comparado con los resultados computacionales obtenidos por (Kanna et al., 2006) y (Erturk, 2008) y los resultados experimentales obtenidos por (Armaly et al., 1983).

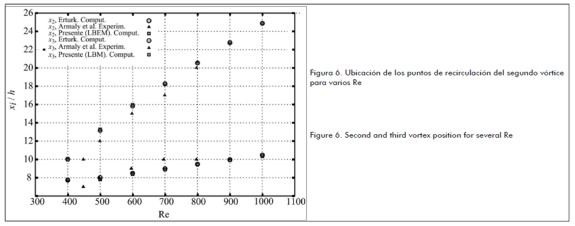
En la figura 6 se muestran los puntos de recirculación del vórtice que se genera en la pared superior del canal y es comparada, al igual que en la figura 5, con los resultados numéricos y experimentales de otros autores.

En la tabla 1 se presentan los resultados numéricos obtenidos de las coordenadas de los puntos de recirculación, logrados en la simulación del flujo mediante el uso de los LBM.

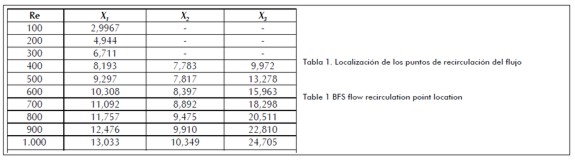
El cálculo de la coordenada de los puntos de recirculación se realizó en toda la dirección x. Se utilizó la velocidad del nodo fluido inmediatamente después de la pared inferior (y = 2), para determinar la coordenada x₁ de la primera recirculación, y del nodo fluido inmediatamente anterior de la pared superior (y = N_y -1) para determinar las coordenadas x₂ y x₃ de la segunda recirculación.

Conclusiones

Se ha presentado una solución numérica del flujo bidimensional por medio de un escalón y en estado estable utilizando el método de la ecuación reticular de Boltzmann. En la simulación se utilizó un perfil de velocidad parabólico a la entrada del flujo y la condición de derivada nula a la salida. La salida se ubicó a una distancia, aguas abajo, del escalón, lo suficientemente alejada de él para que los vórtices que se generan en el flujo no se viesen afectados por la condición de salida. Se utilizaron varios tamaños de malla, desde 850 x 52 para Re = 100, hasta 4.250 x 252 para Re = 1.000. El método de la ecuación reticular de Boltzmann ha demostrado dar resultados numéricos bastante exactos para la simulación de flujos laminares estables con presencia de vórtices.

Se ha revelado un punto importante en la recirculación que genera el flujo en la pared superior. Esta recirculación reflejó un comportamiento de un solo vórtice para todos los números de Re, a diferencia de la simulación para el Re = 800, donde se revelaron tres vórtices en la misma recirculación (ver figura 4.). Los autores creen que dicho comportamiento es debido a que el número de Re = 800 es un punto de transición del flujo y que a partir de este Re el flujo no es totalmente estable.

Referencias

Armaly, B. F., Durst, F., Pereira, J. C. F., Schonung, B., Experimental and theoretical investigation of backward-facing step flow., Journal of Fluid Mechanics, 127, 1983, pp. 473-96.         [ Links ]

Barton, I. E., The entrance effect of laminar flow over a backward -facing step geometry., Int J. Numer. Methods Fluids, 25, 1997, pp. 633-44.         [ Links ]

Biagioli, F., Calculation of laminar flows with second-order schemes and collocated variable arrangement., Int J. Numer. Methods Fluids, 26, 1998, pp. 887-905.         [ Links ]

Bouzidi, M., dÂ'Humieres, D., Lallemand, P., Luo, L., Lattice Boltzmann Equation on a Two-Dimensional Rectangular Grid., Journal of Computational Physics, 172, 2001, pp. 704-717.         [ Links ]

Dieter, A. Wolf-Gladrow., Lattice-Gas Cellular Automata and Lattice Boltzmann Models, Springer (ed.), 2000, pp. 40-65        [ Links ]

Erturk, E., Numerical solution of 2D steady imcompressible flow over a backward-facing step, Part I: High Reynolds number solutions., Computer & fluids, 37, 2008, pp. 633-55.         [ Links ]

Florez, S. E., Cuesta, I., Salueña, C., Flujo de Poiseuille y la cavidad con pared movil calculado usando el método de la ecuación de lattice Boltzmann., Ingeniería & Desarrollo, 24, 2008, pp. 117-32.         [ Links ]

Frisch, U., Hasslacher, B., Pomeau, Y., Lattice-gas automata for the Navier-Stokes equation., Phys. Rev. Lett, 56, 1986, pp.1505-1515.         [ Links ]

Gresho, P.M., Gartling, D.K., Torczynski, J.R., Cliffe, K.A., Winters K.H., Garratt T.J., Is the steady viscous incompressible two-dimensional flor over a backward-facing step at Re =800 stable?., Int J. Numer., Methods Fluids, 17, 1993, pp. 501-41.         [ Links ]

He, X., Luo, L-S., Theory of the lattice Boltzmann method: From the Boltzmann equation to the lattice Boltzmann equation., Phys. Rev. E, 56 (6), 1997, pp. 6811-17.         [ Links ]

Kanna, P. R., Das, M. K., A short note on the reattachment length for BFS problem., Int J. Numer. Methods Fluids, 50, 2006, pp. 683-692.         [ Links ]

Keskar, J., Lyn, D.A., Computation of laminar backward-facing step flow at Re = 800 with spectral domain decomposition method., Int. J. Numer, Methods Fluids, 29, 1999, pp. 411- 427.         [ Links ]

Latt, J., Choice of units in lattice Boltzamnn Simulation., Lattice Boltzmann Howtos: http://www.lbmethod.org/howtos:main. 2008.         [ Links ]

Maxwell, B. J., Lattice Boltzmann methods in Interfacial Wave Modelling., Ph. D. Tesis. Edinburgh's University, 1997.         [ Links ]

Quian, Y., d'Humieres, D., Lallemand, P., Lattice BGK models for Navier-Stokes Equation., Europhys. Lett., 17, 1992, pp.479-84.         [ Links ]

Sheu, T., Tsai, S., Consistent Petrov Galerkin finite element simulation of channel flows., Int J. Numer. Methods Fluids: 31,1999, pp. 1297-310.         [ Links ]

Succi, S., The lattice Boltzmann Equation for Fluid Dynamics and Beyond. Oxford (ed.), 2001, pp. 64- 93.         [ Links ]

Zou, Q., He, X., On pressure and velocity boundary conditions for the lattice Boltzmann BGK model. Phys Fluids: 9, 1997, pp. 1591-1598.         [ Links ]