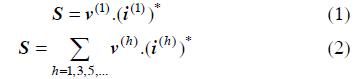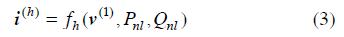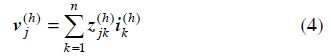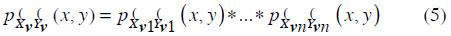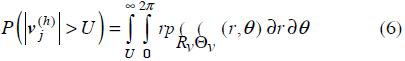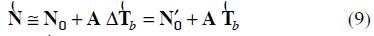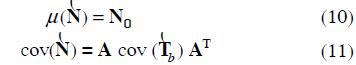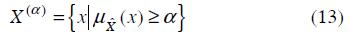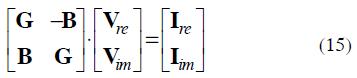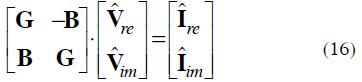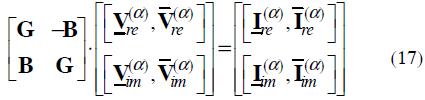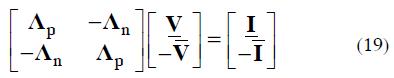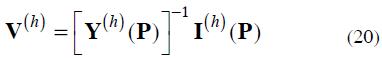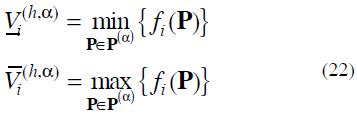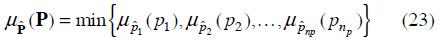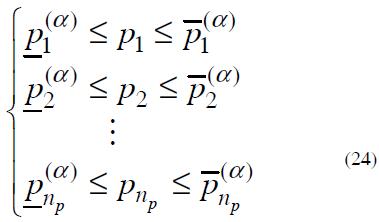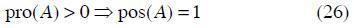Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Ingeniería e Investigación
versão impressa ISSN 0120-5609
Ing. Investig. v.31 supl.2 Bogotá out. 2011
An overview of approaches for modelling uncertainty in harmonic load-flow
Revisión general de las metodologías para el modelado de las incertidumbres en el cálculo del flujo de cargas armónicas
A. A. Romero1, H. C. Zini2, and G. Ratta3
1 Received the Electrical Engineer degree in 2002, at the ''Universidad Nacional de Colombia (UNC)'' and his Ph.D. at the ''Instituto de Energía Eléctrica, Universidad Nacional de San Juan'' (IEE-UNSJ) in 2009. Currently, he is with the IEE-UNSJ, Argentina. (e-mail: aromero@iee.unsj.edu.ar).
2 Received his electrical engineering degree from the IEE-UNSJ, Argentina, in 1985, and its PhD. degree at the IEE-UNSJ in 2002. Currently he is with IEE-UNSJ, Argentina (e-mail: zini@iee.unsj.edu.ar).
3 Received his Electromechanical Engineering degree from Universidad Nacional de Cuyo-Argentina in 1974. Currently, he is director of the IEE-UNSJ, Av. Libertador San Martín 1109 Oeste, San Juan Capital, Argentina (email: ratta@iee.unsj.edu.ar).
ABSTRACT
Harmonic distortion is a growing problem in all power systems (PS) around the world due to the increasing use of electronic power devices and nonlinear loads (NLL). Several methods have been developed for the computational analysis of PS harmonic load-flow (HLF). These approaches allow harmonic distortion to be estimated at each PS bus when NLLs (the harmonic sources) are distributed throughout a whole network. Some widely accepted deterministic formulations are used in HLF analysis; however, harmonic distortion in PS is a time-varying phenomenon because both linear loads (LL) and NLLs change non-predictably all the time. Moreover, network configuration also varies and such considerations make HLF calculation a mathematical problem which must be able to model the uncertainty associated with input data. Some approaches based on probability theory and others using fuzzy sets and possibility theories have been proposed for modeling such uncertainty. This paper was thus aimed at providing an overview regarding these approaches. The main HLF formulations within probabilistic and possibilistic frameworks have thus been introduced and some numerical comparisons have been made to clarify some concepts raised.Index terms: fuzzy set, harmonic distortion, power system harmonics, probability, statistical analysis, uncertainty.
RESUMEN
Debido a la creciente utilización de dispositivos basados en electrónica de potencia y de otras cargas de características no lineales, es que la distorsión armónica en las señales de tensión y de corriente es un problema que va en aumento en todos los sistemas de suministro de energía eléctrica en el mundo. En este contexto, varios métodos han sido desarrollados para el cálculo y análisis computacional del flujo de cargas armónicas en las redes eléctricas. Tales métodos permiten estimar la distorsión armónica en cada barra del sistema eléctrico cuando las cargas no lineales, que son las fuentes de armónicos, se encuentran distribuidas en toda la red. Entre de los métodos para calcular el flujo de cargas armónicas existen algunas formulaciones deterministas que son bien conocidas y ampliamente aceptadas. Sin embargo, la distorsión armónica en el sistema es variable en el tiempo porque tanto las cargas lineales como las no lineales cambian de una manera no predecible, y además, la configuración de la red eléctrica también varía. Esta última consideración hace que el cálculo del flujo de cargas armónicas sea un problema matemático que debe ser capaz de incluir en el modelado las incertidumbres asociadas a los datos de entrada. Para modelar tales incertidumbres se han propuesto en la literatura algunas metodologías de cálculo basadas en la teoría de la probabilidad, y otras basadas en las teorías de los conjuntos difusos y de la posibilidad. Por lo tanto, el objetivo de este artículo es el de ofrecer un panorama completo en lo referente a tales metodologías de cálculo. En particular, las principales formulaciones probabilistas y posibilistas serán presentadas. Finalmente, algunas comparaciones numéricas serán desarrolladas en un sistema eléctrico estándar con el propósito de dar claridad a algunos de los conceptos acá desarrollados.Palabras claves: Conjuntos difusos, distorsión armónica, armónicos en sistemas de potencia, probabilidad, análisis estadísticos, incertidumbre.
1. Introduction
Harmonics exist due to nonlinear loads (NLLs), (IEEE, 1992b). NLLs are increasing in all power systems (PS) due to the widespread use of electronic devices; harmonic distortion in both voltage and current is thus growing (IEEE, 1993a).
Mathematical models and computational programmes have been developed to study harmonics-related problems, for example, to evaluate the effect of connecting large NLLs or capacitor banks, to design harmonic filters, to investigate causes and solutions for existing harmonic overload, to investigate compliance with standards, etc.
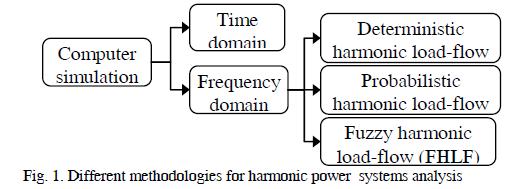
Figure 1 depicts the basic approaches to harmonic calculation; i.e. the second column refers to the approaches used for modelling system behaviour from an electric (physical) point of view, whereas the third column refers to whether and how randomness and uncertainty are modelled.
Time domain analysis is usually carried out using programmes for electromagnetic transient calculations, such as EMTP, which resolve the system of differential and the algebraic equations describing the dynamics of the components (transformers, lines, reactors, capacitors, etc.) and the constraints imposed by Kirchoff's laws. The outputs of these programmes are given in voltage or current waveforms; harmonic components are computed by Fourier analysis of a period for such waveforms after they have reached steady
Due to the computational effort involved, time domain techniques are almost exclusively applied to studying small nonlinear circuits or specific electronic power devices.
Harmonics in large PSs are almost exclusively calculated using frequency domain analysis-based methods, known as harmonic load-flow (HLF). An HLF generalises the methods developed for AC power-flow, representing the harmonic components through phasors associated with sinusoidal magnitude at harmonic frequencies (Herraiz et al, 2003).
A DHLF calculation assumes that all the relevant parameters are known. It should be noted, however, that such studies only provide a static image of a complex and varying situation. In fact, both linear (LL) and NLLs are constantly changing in a non-predictable way which makes harmonic distortion become a stochastic phenomenon. Taking this situation into account, and recognising the high cost involved in completely avoiding any risk associated with excessive harmonic levels, IEC and IEEE standards regarding harmonic distortion have been formulated on a probabilistic basis, stating, for example, that certain levels of harmonic distortion should not be exceeded more than 5% of the time.
Different methodologies modelling the stochastic nature of harmonic distortion, using probability theory, have been developed, thus giving rise to probabilistic HLF (PHLF).
Probability theory is, in principle, the natural tool for modelling random behaviour. However, there are some issues concerning its practical application to PS studies; i.e., probabilistic models assume that uncertain parameters can be described through probability distribution functions. Nevertheless, there is a lack of information for determining these distributions or their parameters in many practical cases.
Information regarding LL and NLL level and characteristics in practice frequently comes from experts' judgment. For example, an expert may describe a load by saying that it could be between 80 MVA and 100MVA, 90 MVA being the most ''possible'' value. Regarding the power factor, the expert might estimate it as being within a range, say from 0.87 to 0.9. She could estimate that between 70% and 80% of total load is linear and 30%-40% of such percentage might be due to induction motors, and so on. Such information is generally incomplete, imprecise, contradictory, or deficient in some other way.
In order to apply probabilistic methods, such uncertain parameters have to be assigned probability distribution functions having a certain mean, variance, etc. Clearly, this can only be done quite arbitrarily.
Such difficulties also exist in many other areas of electric engineering, meaning that novel possibility theory has been found to be a useful alternative to probability theory in dealing with this kind of uncertain information.
Like models based on probability, those based on possibility rely on measurements quantifying uncertainty or likelihood, and allow calculating how these are propagated from the input parameters of a system into its output. Possibility theory can be suitably formulated in terms of fuzzy numbers (FN), hence taking advantage of many of the developments in this area. In addition, models based on possibility theory are usually simpler and computationally more efficient than their probabilistic counterparts.
Possibility and fuzzy set theories are currently being used and investigated for HLF calculation, thus giving place to the so-called fuzzy harmonic load-flow (FHLF).
This paper thus tries to provide an overview of both probabilistic and fuzzy methods and makes numerical comparisons to enhance clarity regarding the main differences in such formulations.
2. Deterministic Harmonic Load Flow (DHLF)
A complete review of the main approaches regarding DHLF is presented in reference (Herraiz et al, 2003); other key articles concerning the subject describe frequency domain models for electric PS components (IEEE Publication, 1998; Arrillaga et al, 1995).
DHLF formulation can be classified according to the hypothesis on which its models have been based. The two main alternatives concern whether to consider the influence of the harmonics in the applied voltage on the current flowing through nonlinear devices and whether to consider harmonic components in power balance equations, i.e. whether equation (1) or (2) should be applied to express load power consumption.
According to the hypotheses, the following three main deterministic formulations may be stated: harmonic penetration (HP), iterative harmonic penetration (IHP) and complete HLF (CHLF). HP designates those methodologies neglecting harmonic interaction and influence of the harmonic components on power balance.
On the other hand, IHP and CHLF refer to different approaches for dealing with the nonlinear set of equations arising when a harmonic interaction is modelled. IHP and CHLF formulations are clearly more accurate than the simpler HP. However, comparisons reported in (Herraiz et al, 2003) and (Sainz,1995) have revealed that errors due to the influence of harmonics in (2) are usually negligible. Moreover, because they require precise knowledge about NLL characteristics and parameters, CHLF and IHP are mainly applied to detailed studies where few NLLs are the dominant harmonic sources.
Experience has thus shown that the non-interactive HP method is sufficient for ordinary harmonic studies and will therefore be set out below.
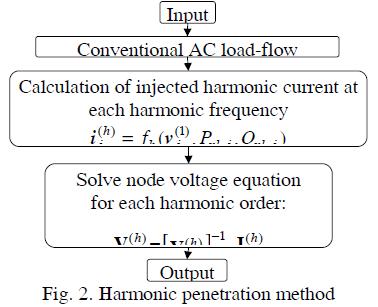
A. Harmonic penetration (HP)
The HP method assumes that voltage distortion does not influence the harmonic content in the current flowing through nonlinear devices and that power balance is not influenced by harmonic components. Such assumptions led to a linear model thus rendering a methodology, particularly simple from the numerical point of view.
Due to the first assumption, NLLs connected at node j, can be modelled by means of expressions like:
where i(h)is the hth harmonic component of the current flowing through the NLL, ƒh is a function depending on load characteristic, 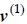 the power frequency component of the applied voltage, and Pnl, and Qnl NLL power consumption. While Pnl, and Qnl are known data, the bus voltage at power frequency is obtained through a conventional AC power-flow, which is the first step in the HP methodology. In this conventional AC power-flow, LL and NLLs are modelled as a whole PQ load4 , neglecting power consumption due to the harmonic components (expression (1) is applied).
the power frequency component of the applied voltage, and Pnl, and Qnl NLL power consumption. While Pnl, and Qnl are known data, the bus voltage at power frequency is obtained through a conventional AC power-flow, which is the first step in the HP methodology. In this conventional AC power-flow, LL and NLLs are modelled as a whole PQ load4 , neglecting power consumption due to the harmonic components (expression (1) is applied).
After the conventional AC load-flow is computed, each NLL is replaced by a current source connected from earth to the bus, equal and opposite to that calculated using equation (3). This leads to a linear circuit where each harmonic bus voltage order could be calculated by solving the circuit equations with the corresponding harmonic sources and impedance modelling the linear components, calculated at the corresponding harmonic frequency.
The HP methodology is illustrated in Figure 2, where V( ) is
the vector of harmonic node voltages of order h; Y( ) the system bus admittance matrix evaluated at the frequency of the h"1 harmonic order with the NLLs replaced by current sources; and V ) the vector of injected harmonic currents of order h. Entries of v ) are zeros for buses without NLLs.
3. Probalistic Harmonic Load Flow (PHLF)
The first contribution to probabilistic modelling of AC power-flows was presented around the mid-1970s in(Allan et al, 1974). In this pioneering proposal, loads were considered as independent random variables and a DC model was used for the PS. This first proposal has since then been largely improved, but it was not until the mid-1980s that these ideas were applied to HLF. A complete review of stochastic modelling techniques for HLF is presented in (Baghzouz, 2002; Ribeiro, 2009).
Several probabilistic methodologies have been proposed based on different probabilistic hypothesis, models and techniques, (Esposito et añ, 2001a; Esposito et al, 2001b). In addition to these probabilistic features, they also differ in the underlying electric model implemented to describe the harmonic behaviour of the network. Both modelling areas are not independent, however, as the feasibility of some probabilistic approaches is conditional on the nature and complexity of the electrical model.
Three main PHLF approaches can be recognised in the pertinent literature: analytic methods based on the HP method, analytic methods based on a linearization of the HLF, and Monte Carlo simulations (MCS).
A. Analytic methods based on the HP formulation
It has been shown above that neglecting harmonic interaction leads to a linear model where the hth harmonic component of the voltage at node j can be written as
where: 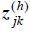 is the harmonic transfer impedance between nodes j and k (self-impedance when j = k), and
is the harmonic transfer impedance between nodes j and k (self-impedance when j = k), and 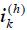 is the hth harmonic component of the current source that models the NLL connected to node k.
is the hth harmonic component of the current source that models the NLL connected to node k.
In PHLF, the injected currents 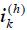 are random phasors,
are random phasors, 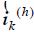 which models the stochastic behavior of the NLLs.
which models the stochastic behavior of the NLLs.
Since the modulus and phase of 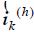 (or its real and imaginary part) are usually random dependent variables, its stochastic behavior is described by joint probability density functions (JPDF)
(or its real and imaginary part) are usually random dependent variables, its stochastic behavior is described by joint probability density functions (JPDF) 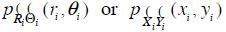 where
where 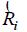 and
and 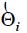 are the modulus and phase of
are the modulus and phase of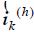 and
and 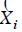 and
and 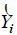 are its real and imaginary parts.
are its real and imaginary parts.
Let 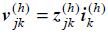 be the hth harmonic component of v(jh) due to the current
be the hth harmonic component of v(jh) due to the current 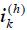 injected by nonlinear load at node k.
injected by nonlinear load at node k.
Since 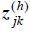 is a constant (nonrandom) phasor, the JPDF of the modulus and phase of
is a constant (nonrandom) phasor, the JPDF of the modulus and phase of 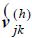 can be easily obtained by properly scaling and shifting that of
can be easily obtained by properly scaling and shifting that of 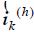 according to the modulus and phase of
according to the modulus and phase of 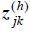 .
.
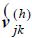 have been obtained, the total harmonic bus voltage
have been obtained, the total harmonic bus voltage 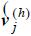 can be written as the sum of n random phasors:
can be written as the sum of n random phasors: 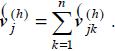
At this point, and to keep numerical complexity reasonable, most of the proposals assume statistical independence ( amongst the random variables 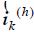 , clearly implying the independence of
, clearly implying the independence of 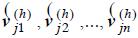 . The JPDF of the real and imaginary parts of
. The JPDF of the real and imaginary parts of 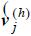 can thus be theoretically obtained by convoluting bi-variable functions; i.e.:
can thus be theoretically obtained by convoluting bi-variable functions; i.e.:
where 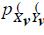 and
and 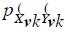 are de JPDF of the real and imaginary part of
are de JPDF of the real and imaginary part of 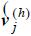 and
and 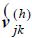 respectively.
respectively.
Such convolutions are usually avoided because they are numerically very extensive. If a relatively large number of phasors have to be added and none of them is dominant, then the central limit theorem can be applied.
The probability of the modulus of the harmonic voltage is obtained by integrating the JPDF of 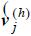 :
:
where 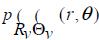 is the
is the 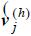 JPDF.
JPDF.
B. Analytic methods based on DHLP linearisation
An alternative analytical approach known as first-order PHLF, (Esposito et al, 2001a) is essentially based on the linearisation of the system of real equations established in DHLF formulation (see section 2) around the expected (mean) values.
Although linearisation clearly implies a loss of accuracy, this approach allows modelling probabilistic dependence between random variables, which is not possible in the previously described methodology.
The mean and variance of the magnitude for each harmonic node voltage are calculated from the DHLF system of equations, and from the mean and covariance matrices of the input variables. Let the DHLF system of equations be expressed in a compact form as:
( where, 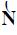 is the vector of random output variables, including the magnitude of the harmonic node voltages for all harmonic order, and
is the vector of random output variables, including the magnitude of the harmonic node voltages for all harmonic order, and 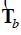 is the input vector, which includes random and deterministic variables, i.e. generator voltage magnitude and power frequency generated active power, active and reactive power of linear loads at the fundamental frequency and the total active and apparent power of nonlinear loads, etc.
is the input vector, which includes random and deterministic variables, i.e. generator voltage magnitude and power frequency generated active power, active and reactive power of linear loads at the fundamental frequency and the total active and apparent power of nonlinear loads, etc.
Let μ( 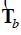 ) be the vector of expected values for components of
) be the vector of expected values for components of 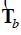 , and N0 the solution of (7) with μ(Tb) at the right hand side:
, and N0 the solution of (7) with μ(Tb) at the right hand side:
By linearizing (7) around N0 and considering (8), then:
( with 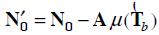 , A is the inverse of the Jacobian matrix of ƒ (N) evaluated at N0, and
, A is the inverse of the Jacobian matrix of ƒ (N) evaluated at N0, and 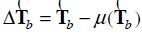 .
.
Equation (9) expresses each random element of the vector 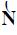 as a linear combination of the random elements of the vector
as a linear combination of the random elements of the vector 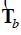 ; hence, the mean and covariance of
; hence, the mean and covariance of 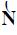 can be written as:
can be written as:
A further improvement for this methodology, called PHLF for percentile evaluation, (Esposito et al, 2001b), goes a step further by also calculating the third and fourth moments (skew and kurtosis) of the probability distribution functions. This set of parameters is enough to completely characterise the Pearson distributions which, according to some measurement systems, seem to be the best fitting of the probability distribution functions for harmonic voltages in their higher percentiles.
C. Numerical analysis using the Monte Carlo simulation
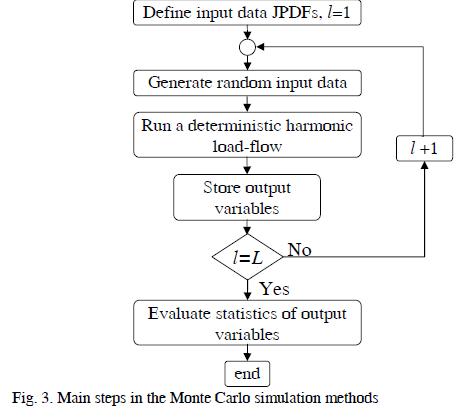
MCS is a well-known technique which is widely used in many different areas. It consists of running a large number of DHLF simulations with different input variables which are randomly selected according to their probabilistic distribution functions. The set of output variables so obtained is a sample from which the probabilistic distribution of the whole population can be estimated. Clearly, the confidence of the results increases with the number of simulations. Figure 3 shows the main steps in MCS.
MCS methods are very flexible since any system parameter can be assumed to be a random variable with adequate formulations and because it is possible to consider probabilistic dependence among them.
It is clear that any DHLF can be implemented, and several hypotheses can be advanced regarding dependence between different sets of random variables. Both aspects strongly influence the computational effort which is, however, usually very high since a large number (thousands) of deterministic simulations are necessary for obtaining accurate results, (Anders, 1989).
D. Final remarks regarding the PHLF
Analytical methods impose some constraints for providing accurate results: random variables have to be independent, and no highly dominant NLL should exist; these two conditions are not always met in practical situations.
Linearization-based analytical methods do not impose particular constraints and allow modelling random LLs. Errors due to linearisation depend on the standard deviation of the input variables which must then be limited.
MCS are very flexible; in principle, methods based on them could manage any kind of stochastic variables, and could be associated with any physical model of the harmonic behaviour of a network (HP, IHP or CHLF). It is, however, recognised that MCS are computationally very demanding.
It should be noted that whatever probabilistic method is applied, the accuracy of the results strongly depends on the accuracy of the probability distribution functions assigned to the random input variables. This is typically one of the most critical issues in HLF studies, especially regarding the composition of LLs and the nature and operating mode of medium and low power electronic devices.
4. Fuzzy Harmonic Lad Flow
Fuzzy set theory has begun to be applied in different areas of electric engineering that involve complex input parameters known with uncertainty. Even though HLF has this characteristic, research regarding application of fuzzy sets to this area is rather new. The first bibliographic reference on the subject was (Hong et al, 2000); more in-depth approaches substantially improving the former were published in(Romero et al, 2008b; Romero et al, 2011). This section briefly presents the main features of the FHLF proposals analysed in the current state of the art overview; however, to enhance clarity, some basic aspects of fuzzy set and possibility theories will be briefly set out.
A. Possibility measures and fuzzy numbers
A membership function maps x elements of a given universal set X, into real numbers in [0, 1]; thus, a membership function can be denoted as follows:
The support of a FN 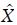 within universal set X is the crisp set that contains all the elements x of X that have non-zero membership grades in
within universal set X is the crisp set that contains all the elements x of X that have non-zero membership grades in 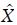 i.e.
i.e. 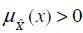 . The core of
. The core of 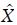 within a universal set X is the crisp set characterised by complete and full membership of set
within a universal set X is the crisp set characterised by complete and full membership of set 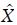 , i.e.
, i.e. 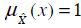 .
.
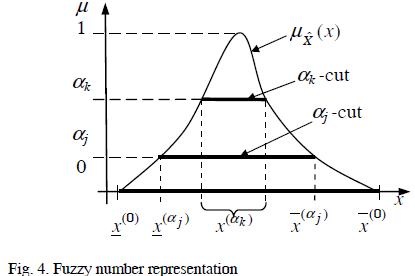
One of the most important concepts of FN is the concept of α-cut. Given a FN 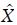 defined on X and any number α ∈[0,1], the α-cut of
defined on X and any number α ∈[0,1], the α-cut of 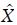 , denoted
, denoted 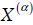 , is the crisp set:
, is the crisp set:
i.e., the α-cut of a FN is the crisp set X(α) containing all the elements of universal set X whose membership degrees in X are greater than or equal to the specified value of α. This concept is illustrated in Figure 4.
FNs and probability distributions play analogous roles in possibility and probability theories, respectively, (Klir et al, 1995). The generic FN shown in Figure 4 introduces the notation used in the following sections.
B. Hong et al. FHLF approach (Hong et al, 2000) (FHLF).
In the DHLF case, the hth harmonic bus voltages can be obtained by solving the system of equations (see Figure 2):
Alternatively, and dropping superscript (h) for the sake of simplicity, (14) can be written as:
where, Ire = Re(I) , Iim = Im(I) and similarly for Vre and Vim , G = Re(Y) and B = Im(Y).
FHLF assumes that both the LLs and the impedances modelling the PS are certain (crisp, non-fuzzy) parameters (i.e. matrices Y, G and B are deterministic) while the injected currents modelling the NLLs are uncertain and modelled through FNs, quantifying the uncertainty of its real and imaginary part, thus making Vre and Vim uncertain.
This situation is modelled by simply replacing the vectors of crisp parameters Ire and Iim by FN vectors, which will be denoted as 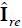 and
and 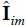 , and also Vre and Vim by
, and also Vre and Vim by 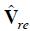 and Vim. Thus, (15) becomes the fuzzy system of equations:
and Vim. Thus, (15) becomes the fuzzy system of equations:
A simple way to solve fuzzy equation systems is by solving each system of interval equations corresponding to its (theoretically infinite) α-cuts.
Designating 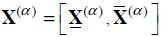 the vector of the α-cuts
the vector of the α-cuts
of components of 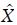 , where
, where  and
and  are the vectors of the lower and upper limits of the intervals. Thus, using this notation, the interval equation associated with the α-cut of equation (16), becomes:
are the vectors of the lower and upper limits of the intervals. Thus, using this notation, the interval equation associated with the α-cut of equation (16), becomes:
In spite of its simplicity, different solutions can be conceived for the interval and fuzzy equations depending on the exact meaning given to the equal sign in this context. Some relevant kinds of solution sets were described in (Romero et al, 2008b), however here only the simplest solution known as the interval algebraic solution, (IAS)' (CSS in the fuzzy case, (Bukcley et al, 1991) is the one applied in (Hong et al, 2000).
The IAS for a system of n interval equations can be found by solving a linear system of 2n crisp equations providing the limits of the interval solution (Friedman et al, 1998). Specifically, if:
is the set of interval equations, the IAS satisfies the following equation:
where, Λp is the matrix of the positive entries of Y (all its negative entries replaced by zeros), and Λn is the matrix of the negative entries of Y (all its positive entries replaced by zero), i.e., ( Y = Λp + Λn ).
This system of crisp equations can always be formulated, regardless of whether the solution exists; if it does not exist, some of the intervals turn out to be impossible (i.e.  .
.
Reference (Friedman et al, 1998) suggests reversing these improper intervals to get a meaningful result, called 'weak solution'; however, such a result is not a solution in any mathematical sense, and it can either over- or under-estimate real uncertainty in harmonic voltage.
Reference (Romero et al, 2008b) demonstrated that the IAS set is not exactly the desired result in the context being analysed because, when the right-hand side intervals model inputs known to have uncertainties (e.g. harmonic currents injected in different buses), all vectors on the right-hand side are possible, and all the associated voltages are of interest. Moreover, even though LLs could have a major influence on the HLF, (Chang, 2003), uncertainties in their power and composition are not modelled and cannot be handled in the proposed formulation. Fuzzy real and imaginary parts of harmonic voltages are obtained instead of the more useful fuzzy magnitudes.
C. The possibilistic harmonic load flow (NFHLF)
The analysis of Hong et al.,'s FHLF approach presented in (Romero et al, 2008b) reveals the aforementioned drawbacks, which were then addressed through research published in, (Romero et al, 2008a; Romero et al, 2008b; Romero et al, 2011).
In those papers, a new FHLF (hereafter noted as NFHLF to differ from that of Hong et al.) has been founded on the proposed possibility theory. NFHLF relies on nonlinear programming techniques and allows for efficiently modelling uncertainties regarding input parameters (LL and NLL) by means of possibility distributions. Expression (14) can be expressed as:
where, the diagonal elements of Y(h) as well as the components of I(h) depend on the characteristics of the LLs and NLLs, described by a set of parameters organised in array P.
From (20), the magnitude of each node voltage can be defined as a function of parameters P, i.e.:
with 
When parameters in P are uncertain and described through their joint possibility distribution functions  , the possibility distribution function of vi(h) ,
, the possibility distribution function of vi(h) ,  can be obtained. In particular the limits of each a-cut of
can be obtained. In particular the limits of each a-cut of  can be calculated by solving two optimisation problems:
can be calculated by solving two optimisation problems:
where,  and
and  are the lower and upper limits of the α of
are the lower and upper limits of the α of  and P(α) is the corresponding α-cut of the joint possibility distribution associated to the fuzzy vector
and P(α) is the corresponding α-cut of the joint possibility distribution associated to the fuzzy vector  .
.
When parameters p1, p2, ..., pnp are independent, the joint possibility distribution function  is:
is:
and its α-cuts P(α) are the rectangular domains:
where  and
and  are the lower and upper limits of the α-cut of
are the lower and upper limits of the α-cut of  .
.
As parameters, pk, k=1...np,, have to completely define admittance to ground and injected currents modelling the LL and NLLs, then a proper circuit for modelling the harmonic behaviour of the loads was presented in reference (Romero et al, 2011). Moreover a set of fuzzy parameters for describing the available information regarding load magnitude and composition was selected and described in detail and the relationship between the model and circuit parameters were formulated.
5. Comparative analysis in a 14-bus test system
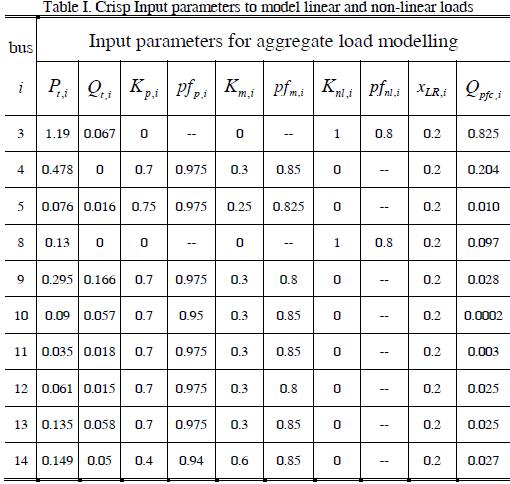
This section presents the results of numerical simulations aimed at showing some comparisons between main proposals exposed in this paper. The following issues are pointed out: Specific load models, compatible with FHLF modelling capability, have been implemented for this test to achieve proper comparison. In effect, the frequency dependence of impedances used to model LLs has been represented according to the aggregate harmonic load model presented in (Romero et al, 2011). However, it was assumed that input parameters defining the electric model of the bus linear load were crisp values (non-fuzzy) in all the simulations shown. Such input parameters are reported in Table 1.
While NFHLF results were harmonic voltage magnitudes' possibility distributions, FHLF output was the possibility of these voltages' real and imaginary components. To compare the results, possibilities of the voltage magnitude have been calculated from real and imaginary FHLF output, assuming possibilistic independency.
MCS were computed to obtain a benchmark for suitable comparison of the results obtained from each fuzzy methodology, i.e. the FHLF and the NFHLF.
The tests were carried out on the IEEE 14-bus harmonic test system. The one-line diagram of this PS and the main parameters of the network are summarised in reference (Chang, 1999). Generators, lines and transformers have been modelled according to the recommendation in (Ranade, 1996). Harmonic filters (all single-tuned) have been modelled as shunt impedances.
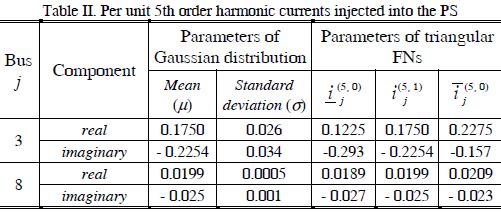
Regarding the uncertain parameters for modelling NLLs, the 14-bus test system contained two harmonic sources, namely two six-pulse converters, one at bus 3 and the other at bus 8. Moreover, considering that all power consumption at buses 3 and 8 was due to these NLLs, then, it was assumed that power consumed by these NLLs varied by 5% concerning their crisp values reported in Table 1. From these uncertain parameters and fr om the mathematical expressions for modelling the nonlinear devices, (Arrillaga et al, 1995), then, the harmonic currents injected at buses 3 and 8 were computed.
Moreover, triangular FNs have been used to model possibility distributions of real and imaginary components of harmonic currents, whereas Gaussian distributions truncated at two standard deviations have been chosen to model the probabilistic ones in the MCS. Table 2 shows possibilistic and probabilistic distribution parameters.
A. Results
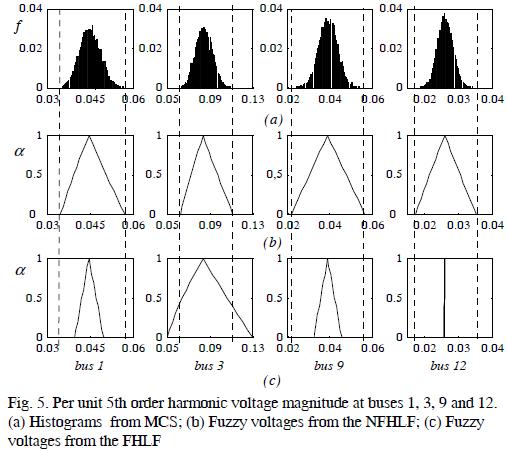
Figure 5 shows the discrete probability density functions and membership functions of 5th order harmonic voltages, in pu, at buses 1, 3, 9 and 12, calculated through MCS, the NFHLF, and FHLF. In particular, histograms for 5th order harmonic voltage were attained after L=10000 random shots for MCS.
B. Discussion
Before making comparisons between the three HLF solutions, considering uncertainties, it should be stated that evidence theory provides a link between possibility theory and probability theory. In fact, when information regarding some phenomenon is given in both probabilistic and possibilistic terms, both descriptions should be consistent (Klir et al, 1995). Two main consistency conditions are that the weakest one can be expressed as follows: an event that is probable to some degree must be possible at least to the same degree. Thus,
The strongest consistency condition requires that any event with nonzero probability must be fully possible.
Considering the aforementioned, and from the results, the following comparisons and conclusions were made.
From a qualitative comparison between possibilistic and probabilistic distributions plotted in Figure 5, it can be noted that plots 5(a) and plots 5(b) showed good agreement between results obtained with NFHLF and MCS in all PS buses. Moreover, as expected, the possibilistic model and the probabilistic MCS kept the coherence imposed on their input variables regarding their output, i.e., i) all probable values of the harmonic voltages were also possible and ii) non-possible values had zero probability.
However, by comparing plots 5(a) with those in 5(c), such coherence was not achieved. In fact, several probable values of the 5th order harmonic voltage magnitude at buses 1, 9 and 12 were not possible in agreement with 5(c) plotted results. Moreover, several possible values of 5th order harmonic voltage magnitudes at bus 3 were not probable as shown in plot 5(a) for that bus. Briefly, results achieved by means of FHLF did not fulfil the two main consistency conditions stated above between probability and possibility functions.
Clearly, over- and under-estimating harmonic voltage uncertainty shown by the FHLF approach did not occur with NFHLF. This conclusion was also proven in (Romero et al, 2008b).
6. Conclusions
An overview of the state of the art regarding HLF calculation has been presented. Two main formulations for considering uncertainty in the analysis have been described, i.e., methods based on probability and on possibility.
To exploit the capability of methodologies based on probability theory, the random behaviour of each stochastic input parameter has to be known and properly described in probabilistic terms. However, this is seldom the case in practical situations, because available evidence about the behaviour of some input parameters (such as linear, motive, nonlinear and capacitive load composition) is rarely based on outcomes from a sufficiently long series of independent random experiments correctly allowing probability density functions to be characterised.
Possibility theory, on the other hand, is ideal for formalising incomplete information expressed in terms of fuzzy propositions. In fact, the available information for modelling uncertainty involved in input parameters for HLF is commonly vague or fuzzy; for instance, judgments such as, ''the LL in bus 5 can be estimated at 10 MW, hardly less than 9 MW or higher than 12 MW; about 35% of it is..., etc''. Similar statements are often the best that one can make about NLLs as well.
A methodology for solving an FHLF where triangular FNs model harmonic injected currents has been proposed in (Hong et al, 2000). However, such fuzzy methodology has some drawbacks, i.e., harmonic voltage over- and under-estimation and inability for modelling uncertainties related to LLs. The latter represents a grave weakness because LLs are usually not well known, and affect the HLF.
A novel NFHLF, proposed in (Romero et al, 2008b) - (Romero et al, 2011), overcomes the drawbacks detected in the previous formulation. Its main characteristics are that it is based on nonlinear programming techniques, thus avoiding the harmonic voltage over- and under- estimation to which FHLF leads. It is capable of modelling uncertainty in both LL and NLLs which are imprecisely known in real PS. It permits the translation of FNs describing uncertain data, like NLL percentage, induction motors, or capacitive compensation connected to a given bus, within the electric fuzzy parameters used in NFHLF.
A comparison between the approaches presented here has been performed in the IEEE 14-bus PS. The tests showed that results obtained with MCS and the NFHLF had good agreement.
The approaches presented here are useful for decision-making regarding uncertainty, harmonic filters and capacitors location, impact of new harmonic load connection, and so on.
7. Acknowledgement
This work was partly financed by the German Academic Exchange Service (Deutscher Akademischer Austauschdienst / DAAD) and the Consejo Nacional de Investigaciones Científicas y Técnicas, CONICET, Argentina.
NOTA DE PIE
4 In an AC power flow, the nodes are defined as: Vð Slack node, the voltage and phase are known; PQ: the active and reactive powers are knwon: and, PV: the active powerand the voltage magnitude are known.8. References
Allan, R. N., Borkowska, B., Grigg, C., Probabilistic Analysis of Power Flows., IEE Proceedings, Vol. 121, No. 12, 1974; pp. 1551 - 1556. [ Links ]
Anders, G. J., Probability Concepts in Electric Power Systems., John Wiley and Sons, Inc., Interscience Publication, 1989. [ Links ]
Arrillaga, J., Arnold, C. P., Computer Analysis of Power System., John Wiley and Sons, Inc., 1995. [ Links ]
Baghzouz, Y., Task Force on Probabilistic Aspects of Harmonics, Time-Varying Harmonics: Part II - Harmonic Summation and Propagation., IEEE Trans. Power Del., Vol. 17, No. 1, 2002, pp. 279-285. [ Links ]
Bukcley, J., Qu, Y., Solving Systems of Linear Fuzzy Equations., Fuzzy Sets and Systems, vol. 43, 1991, pp.33-43. [ Links ]
Chang, G., Task force on harmonics modeling and simulation, Impact of Aggregate Linear Load Modeling on Harmonic Analysis: A Comparison of Common Practice and Analytics Models., IEEE Trans. Power Del., vol. 18, 2003, pp. 625-630. [ Links ]
Chang, G., Task force on harmonics modeling and simulation, Test Systems for Harmonics Modeling and Simulation., IEEE Trans. Power Del.., vol. 14, 1999, pp. 579-585. [ Links ]
Esposito, T., Carpinelli, G., Rossi, F., and Verde, P., Probabilistic Harmonic Power-Flow for Percentile Evaluation., Conference on Electrical and Computing Engineering, Canadian, vol. 2, May, 2001a, pp. 831-838. [ Links ]
Esposito, T., Carpinelli, G., Varilone, P., and Verde, P., First-order Probabilistic Harmonic Power Flow., IEEE Proceedings on Generation, Transmission and Distribution, vol. 148, No. 6, Nov, 2001b, pp. 541-548. [ Links ]
Friedman, M., Ming, M., Kandel, A., Fuzzy Linear Systems., Fuzzy Sets and Systems, vol. 96, 1998, pp. 201-209. [ Links ]
Herraiz, S., Aportaciones al Estudio del Flujo Armónico de Cargas., tesis presentada al Departamento de Ingeniería Eléctrica de la Universidad Politécnica de Cataluña, para optar al grado de Doctor of Philosophy, 2002. [ Links ]
Herraiz, S., Sainz, L., Clua J., Review of Harmonic Load Flow Formulations, IEEE Transactions on Power Delivery, vol. 18, No. 3, July, 2003, pp. 1079-1087. [ Links ]
Heydt, G. T., Electric Power Quality., Stars in a Circle Publications, 1994. [ Links ]
Hong, Y., Lin, J., Liu, C., Fuzzy Harmonic Power Flow Analyses., International Conference on Power System Technology, Proceedings, PowerCon 2000, vol. 1, 2000, pp. 121-125. [ Links ]
IEEE Publication TP-125-0, Task force on harmonics modeling and simulation, Tutorial on Harmonics Modeling and Simulation.,1998 [ Links ]
IEEE Std. 141-1993, IEEE Recommended Practices for Electric Power Distribution for industrial Plants, Red Book, Ch. 9, 1993a [ Links ]
IEEE Std. 519-1992, IEEE Recommended Practices and Requirements for Harmonic Control in Electrical Power Systems, April 1993b [ Links ]
Klir G.J., Yuan B., Fuzzy Sets and Fuzzy Logic, Theory and Applications., Prentice Hall, 1995 [ Links ]
Ranade, S., Task force on harmonics modeling and simulation, Modeling and Simulation of the Propagation of Harmonics in Electric Power Net-works., IEEE Trans. Power Del., Vol. 11, Jan, 1996, pp. 452-465. [ Links ]
Ribeiro, P. F., (ed), Time-Varying Waveform Distortions in Power Systems., John Wiley and Sons, Inc., 2009 [ Links ]
Romero, A.A., Zini, H. C., Ratta, G., Dib, R., A Novel Fuzzy Number based Method to Model Aggregate Loads for Harmonic Load-flow Calculation., Transmission and Distribution Conference and Exposition Latin America, 2008 IEEE/PES, 2008a, pp.1-8. [ Links ]
Romero, A.A., Zini, H.C., Rattá, G., Dib, R., A Fuzzy Number Based Methodology for Harmonic Load-Flow Calculation, Considering Uncertainties., Latin American Applied Research, vol. 38, 2008b, pp. 205-212. [ Links ]
Romero, A.A., Zini, H.C., Rattá, G., Dib, R., Harmonic Load-flow Approach Based on the Possibility Theory., Generation, Transmission & Distribution, IET, vol.5, no.4, April, 2011, pp.393-404. [ Links ]
Sainz, S. L., Estudio de la Formulación y Resolución del Problema del Flujo Armónico de Cargas., tesis presentada al Departamento de Ingeniería Eléctrica de la Universidad Politécnica de Cataluña, para optar al grado de Doctor of Philosophy, 1995 [ Links ]
Xu, W., Component Modeling Issues for Power Quality Assessment., IEEE Power Engineering Review, Nov. 2001, pp. 12-17 [ Links ]