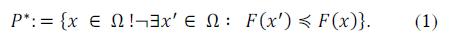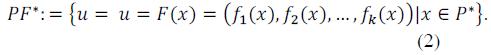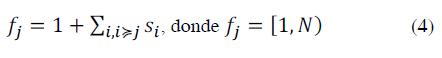Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.31 suppl.2 Bogotá Oct. 2011
Implementation of an evolutionary algorithm in planning investment in a power distribution system.
Implementación de un Algoritmo Evolutivo en la Planeación de Inversiones de un Sistema de Distribución de Energía.
C. A. García Montoya1, S. Mendoza Toro2.
1 Carlos Andrés García Montoya iswith Área Distribución Eléctrica Centro of Empresas Públicas de Medellín, and iscandidateto Magister Engineering of Universidad de Antioquia, Medellín, Antioquia, Colombia (e-mail: carlos.garcia.montoya@epm.com.co).
2 Steiner Mendoza Toro iswith Área Distribución Eléctrica Centro of Empresas Públicas de Medellín, (e-mail: steiner.mendoza@epm.com.co).
ABSTRACT
The definition of an investment plan to implement in a distribution power system, is a task that constantly faced by utilities. This work presents a methodology for determining the investment plan for a distribution power system under a short-term, using as a criterion for evaluating investment projects, associated costs and customers benefit from its implementation. Given the number of projects carried out annually on the system, the definition of an investment plan requires the use of computational tools to evaluate, a set of possibilities, the one that best suits the needs of the present system and better results. That is why in the job, implementing a multi objective evolutionary algorithm SPEA (Strength Pareto Evolutionary Algortithm), which, based on the principles of Pareto optimality, it deliver to the planning expert, the best solutions found in the optimization process. The performance of the algorithm is tested using a set of projects to determine the best among the possible plans. We analyze also the effect of operators on the performance of evolutionary algorithm and results..Keywords: Evolutionary Algorithm, Distribution system planning, SPEA, Multi-objective optimization, optimal investment plan
RESUMEN
La definición de un plan de inversiones a realizar en un sistema de distribución, es una tarea a la que constantemente se deben enfrentar las empresas de distribución. Este trabajo, presenta una metodología para la determinación del plan de inversiones en un sistema de distribución, bajo un horizonte de corto plazo, empleando como criterio de evaluación de los proyectos de inversión: los costos asociados y los clientes beneficiados con su ejecución. Dada la cantidad de proyectos que se ejecutan anualmente sobre el sistema, la definición de un plan de inversiones requiere del uso de herramientas computacionales que permitan evaluar, de un conjunto de posibilidades, la que más se ajuste a las necesidades del sistema y mejores resultados presente. Es por esto que dentro del trabajo, se implementa un algoritmo evolutivo multi objetivo SPEA (Strength Pareto EvolutionaryAlgortithm), el cual, basado en los principios de optimalidad de Pareto, entregan al experto en planeación, las mejores soluciones halladas dentro del proceso de optimización, según los objetivos planteados. El desempeño del algoritmo es probado empleando un conjunto de proyectos, hasta determinar los mejores planes de entre los posibles. Se analiza además, el efecto que tienen los operadores evolutivos sobre el desempeño del algoritmo y los resultados del mismo.Palabras clave: Algoritmos Evolutivos, Planeación de sistemas de Distribución, Optimización Multi objetivo, Plan de inversiones óptimo.
1. Introduction
The mission of the distribution power systems, is primarily the power delivery, when requested and under technical specifications defined by regulators(Bernal, 1998). To ensure that the distribution system to meet this objective, the utilities spends great amount of financial and human resources in planning processes of the system. This process is approached from different perspectives or approaches: some focus on the technical features, others in determining appropriate conditions of service, of course, all this considering the environment and environmental conditions that affect the operation and performance of the system, but finally, pretend comply with the delivery of the product under conditions set and looking for better returns for the utilities (Ferreira et al, 2001).
In the last two decades, the electricity market has been affected by different factors, but most outstanding is the fact that happened to be owned by the state to allow the entry of private investors, forcing it to improve performance, efficiency and obviously, the financial results for those involved in the business. This situation, coupled with the complexity of the distribution system and the primary goal already mentioned, has forced the planning process of the distribution goes from being developed intuitively and at the discretion of expert, now developed using tools to ensure compliance with the requirements and conditions that the market imposes, among them, the expected economic returns and rates of service quality and energy demanded by end-user.
Proper planning of the distribution system, must have a clearly defined horizon, integrating various aspects such as investments required by the system, the costs of operating and maintaining the optimal system design and estimate the long term needs and characteristics of the load served(Khator and Leung, 1997; Fletcher and Strunz, 2007,).
Different approaches and techniques have been proposed for solving the problem of planning; starting with linearized models and other nonlinear solved using classical techniques such as Branch and Bound (Boardman and Meckiff, 1985), and others, by or mixed integer linear programming (Gönen and Foote, 1981). In addition, hybrid techniques have been used or which contain the integration of search concepts with fuzzy techniques, as proposed in (Ramirez and Dominguez, 2006). Since the late 90's, evolutionary algorithms have been used with good results, they present it as a promising solution technique to the problem of distribution planning, both for problems single-objective and multi-objective problems(Bernal, 1998; Ferreira et al, 2001; Khodr et al, 2009;Carreno et al, 2007; Díaz et al, 2002).
In this paper, there is a methodology for defining the optimal investment plan to be implemented in the distribution system in the short term, doing a desk review, and then use a multi objective evolutionary algorithm, which in this case is a SPEA (Strength Pareto Evolutionary Algorithm) (Zitzler and Thiele, 1999), which optimizes the number of customers benefit from implementing the investment plan, the costs of it and the improvements achieved technical and service with its implementation. This methodology defines the investment plan, which generates higher benefits for the distribution company and its customers.
The paper is organized as follows: Section II presents the fundamentals of evolutionary algorithms, with emphasis on the algorithm used (SPEA), section III details the methodology and the algorithm implemented. Then, Section IV presents a description of the case study implemented, moreover, results and discussion, it presents the performance results obtained with the implementation and finally Section V and VI present future work and cite conclusions of the study,respectively.
2. Multi-objective optimization using evolutionary algorithms
Evolutionary algorithms are inspired primarily on the theory of Darwinian natural selection, is therefore that operators have characteristic of this theory, such as: reproduction, competition, random mutation and selection. In general, the algorithm operates by running the operators mentioned in a population, which exists only within an iteration of the algorithm (Rivas et al, 2007).
Different techniques have been developed to solve optimization problems with more than one goal. However, many of them have limitations in trying to solve a problem of this nature. For example, techniques that require evaluating differentiable objective functions and constraints to operate properly. Additionally, many only work with a single solution, making it difficult, obtaining an optimal Pareto front. Evolutionary algorithms have the property, within a single iteration, evaluate and find a group of feasible solutions to the optimization problem, thus achieving relatively easily find a set of solutions that satisfy the optimality conditions of a multi problem objective and does not require knowing if the evaluated functions are differentiable or not. This allows theevolutionary algorithm, it work in complex solution spaces and not necessarily convex, to ensure its operation, in addition to working on Pareto fronts with discontinuities (Coello, 2006).
A. Pareto optimality
Problems with multiple objectives, their main feature is not having a single solution, if not, a set of them, which are identified mainly by the fact that conflict in trying to optimize. The Multi-objective algorithms make use of the concept of so-called Edgeworth-Pareto optimality, which has been called Pareto optimal. This principle states that a solution is optimal if no other solution to reduce or improve any objective without diminishing other simultaneously (Coello, 2006).Are formally defined below, the concepts of Pareto Optimality required for the implementation of Multi objective algorithms (Coello et al, 2007).
a) Pareto dominance: A vector u = (u1;u2, ...,uk) is said to dominate v = (v1,v2, ..., vk)(denoted u ≤ v) if and only if uis partially less than v, i.e., ∀i ∈ {1, 2, ...,k},u ≤ vi ∧ 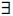 i ∈ {1, 2, ...,k},ui < vi
i ∈ {1, 2, ...,k},ui < vi
b) Pareto Optimality: A solution x ∈ Ωis referred to as Pareto optimal with respect toΩif and only if there is no x' ∈ Ωfor whichv = F(x') = 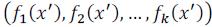 dominatesu = F (x) =
dominatesu = F (x) = 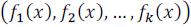
c) Pareto Optimal Set: For a given multi-objective problem F(x), the Pareto optimal set(P*)is defined as:
d) Pareto Front: For a given multi-objective problem F(x) and Pareto optimal setP*, the Pareto front (PF*)is defined as:
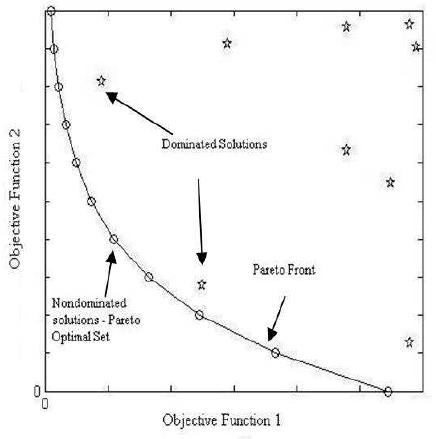
Figure 1. Enlightenment concepts of Pareto Optimality.
Illustratively, in Figure 1.is illustrated the Pareto concept of optimality for the case of a problem with two objectives.B. Algorithm SPEA (Strength Pareto Evolutionary Algorithm)
In evolutionary algorithms based on concepts of Pareto optimality, one of the most outstanding for its good performance is the SPEA (Coello et al, 2007), which was proposed by Zitzler and Thiele in (Zitzler, 1999, pp. 257-271).
This algorithm differs from others of its kind, in that: a) has a population containing external non-dominated individuals, which constitute the Pareto front of the current population, b) The allocation of the fitness to the individuals, is made according to the dominance of external population on individuals in the general population, c) All solutions involved in the selection, without excluding any individual, and d) It uses a clustering method to reduce the size of the external population, and with it also ensures the diversity of the population. For the implemented algorithm, has been used the method clustering Fuzzy C-means (Rui and Wunsch, 2005).
Essential part of the algorithm is the assignment of fitness, which is divided into two parts, depending on the population that is being assigned. In the case of the external population, each solutioni, the external population P'is assigned a real values, £ [0,1), called the force (strength). ƒiValue is assigned using the expression (3), wherenis the number of individuals in the general populationPwhich are dominated byi.
The fitness of individuals j belonging to population P, is calculated by adding the force (strength) of all individuals in the population?' that dominate/, as specified in the expression (4).
3. Implemented methodology
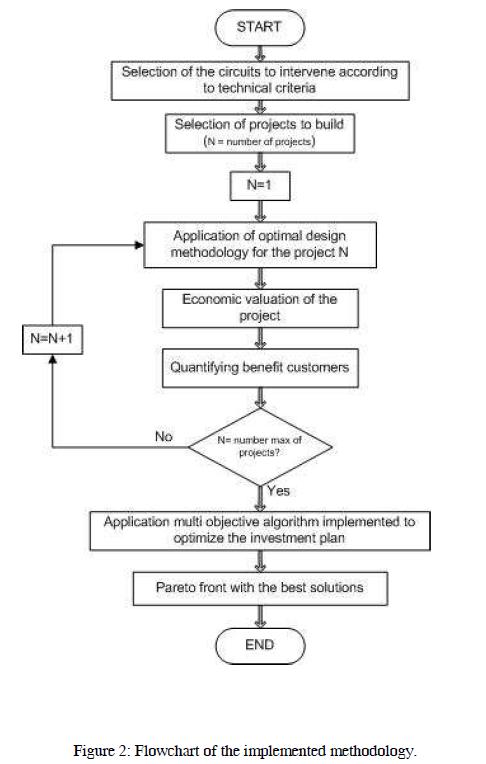
Maintain the distribution system in good condition, requires to constantly invest economic resources, which obviously are not unlimited. This reason generates the need for a methodology to determine which of the works to make in the system have a greater impact in terms of cost benefit to customers or another aspect. In, we can see the flow chart for evaluation of the investment plan of a distribution system. This methodology, start identifying system requirements from the technical point of view tailored to the practices and policies of the utilities. For this, operating criteria are used as limits of chargeability of circuits, maintenance criteria and technical feasibility assessment that require projects to be considered within the plan.
Following completion of the pre-validation are chosen projects that are required more urgently then undergo a process of optimal design of distribution networks or to check the technical conditions of the proposed project. This procedure aims; achieve a higher level of service efficiency and productivity of the system. Economic valuation should be done according to the method of remuneration for the market regulator power of the country concerned or the costs recognized by the commissioning of new assets, which, in Colombian case is CREG, who under the resolution 097 of 2008, determined the costs recognized and useful life for new assets installed in the distribution system (CREG 097, 2008).
Depending on the scenario being evaluated, it may be necessary financial projections and economic feasibility analysis of projects, to complement the financial analysis, but this implementation is not required, given that the planning horizon is one year.
Having completed the selection of projects to be considered in the planning process, is executed on multi-objective algorithm SPEA implemented to define the optimal investment plan under the defined criteria.
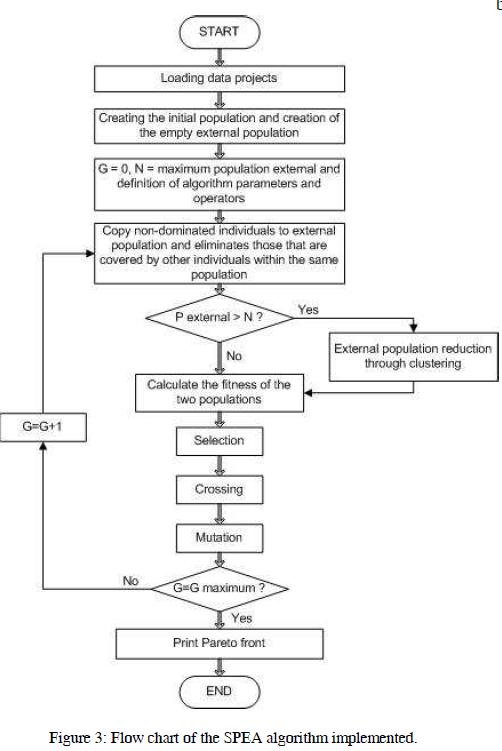
Figure 3. Shows the flow chart of the multi-objective algorithm implemented, which details how it operates.
The SPEA implemented, after loading the projects data, creates a random initial population and external population required by the algorithm. The individuals comprising the population are composed by M projects. Since the encoding used in the model is binary, each of the genes that make individuals can only assume values 1 or 0, indicating that those genes that have value 1, representing the projects included in the investment plan and which are assigned as 0, will not be considered within it. Once defined the parameters of the algorithm, the initial population and the external population, is assess the dominance of individuals in the general population, copying the non-dominated individuals within the external population, which will contain the Pareto front resulting from the optimization process. If the number of individuals who possess the external population, exceeds the value N (maximum number of individuals in the external population), is run an external population reduction by the technique of Fuzzy C-Means clustering. Fitness is then calculated from both populations, consistent with the concepts defined in Section II of this paper.
The genetic operators defined for this algorithm are: a) selection by tournament, b) Cross-homogeneous, which guarantees that the best characteristics of parents are inherited by offspring, and c) random mutation.
4. Case study
Figure 3: Flow chart of the SPEA algorithm implemented.
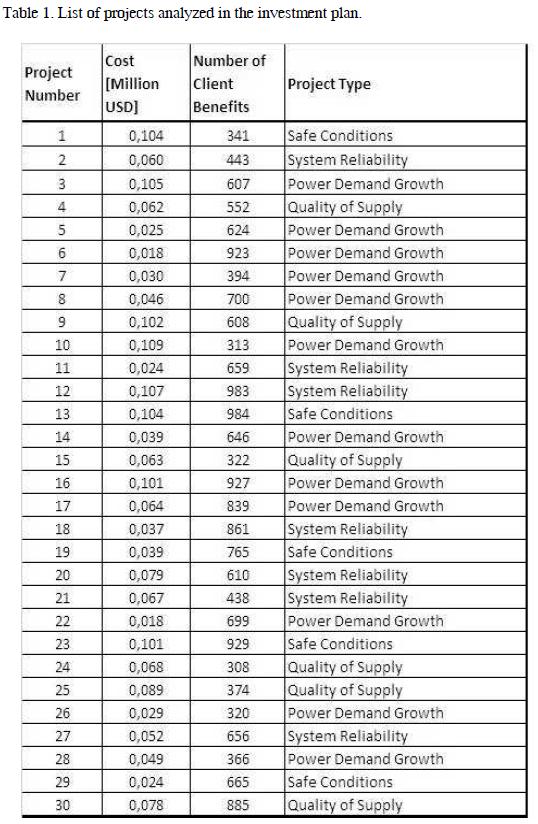
The Table 1, display the thirty projects to be considered in the investment plan, indicating the cost and benefit customers.
The distribution systems planning can be run using different criteria, depending on system needs.
For the selection of projects considered in the plan to optimize within this work, were taken as basic selection parameters: the needs generated by growth in demand, projects to improve system reliability, power quality and improve safe condition of electrical networks. Using these criteria, thirty projects have been identified located in three substations that provide power service in the city of Medellin, and have been evaluated in accordance with the methodology proposed. The cost of the projects is between 0,018 and 0,111 million USD and has estimated a range of clients benefiting from its implementation between 300 and 1000 clients.
5. Results and discussion
The tests performed with the algorithm implemented in the present study, it focused on trying to identify the effect of genetic operators on the performance and results of the optimization process, as well as verify their proper evolution, convergence and process results.
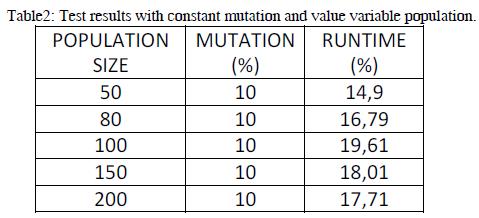
In order to assess the effect of population size on the performance of the algorithm, some tests were performed in which the mutation is held constant and varying the size of the population.
The Table 2 presents a summary of the tests and the runtime of the algorithm. As can be seen, although there is an increase in execution time depending on the size of the population, the increase is negligible considering that it is working on a process that takes seconds to reach convergence.
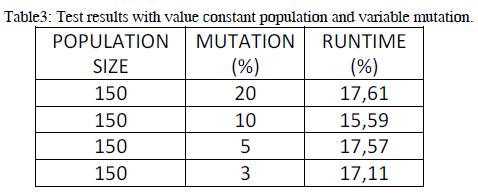
The Table 3 summarizes the tests, leaving a constant population size and varying the value of the mutation. It evidence that changes in mutation do not have a significant impact on runtime.
By validating the little effect of mutation and population size on the execution time, it checked the results obtained during testing, to determine approximately, in the generation what convergence was achieved.
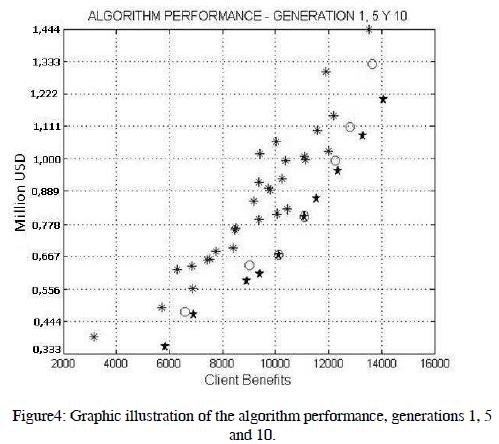
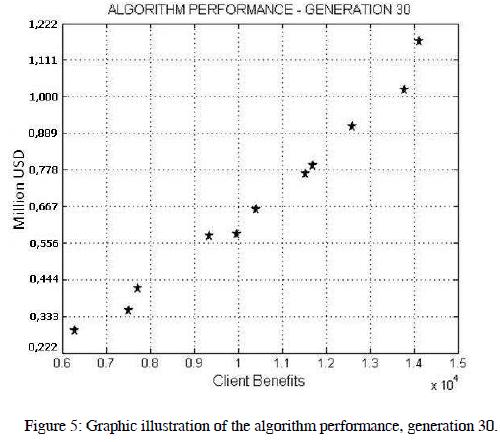
In the Figure 4 evolving illustrates the Pareto front of one of the tests, plottingthe generation one, five and ten. Figure 5 presents the results of the iteration 30, as shown by comparison with Figure 4, once the iteration ten is overcome, not achieved substantial improvements in the Pareto front movement.
Analyzing the overall results of the optimization process and Figures 4 and 5 can be said that although the algorithm is allowed to continue running to the thirty generation without applying another iteration convergence criterion different from the limit of generations, the convergence achieved approximately on ten iterations.
Another important element to note, is that it can see how preserving the diversity of the population throughout the process. This is possible thanks to the method of population reduction by external grouping procedure under the Fuzzy C-Means technique.
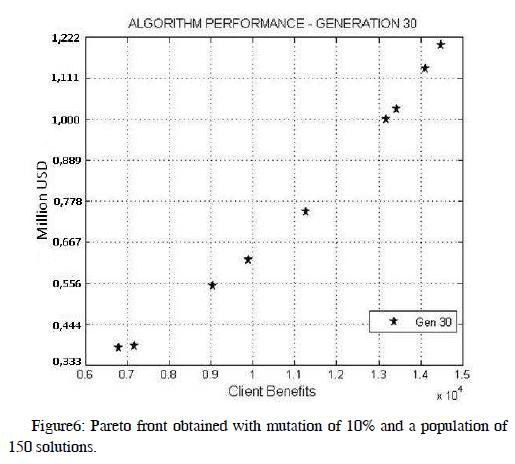
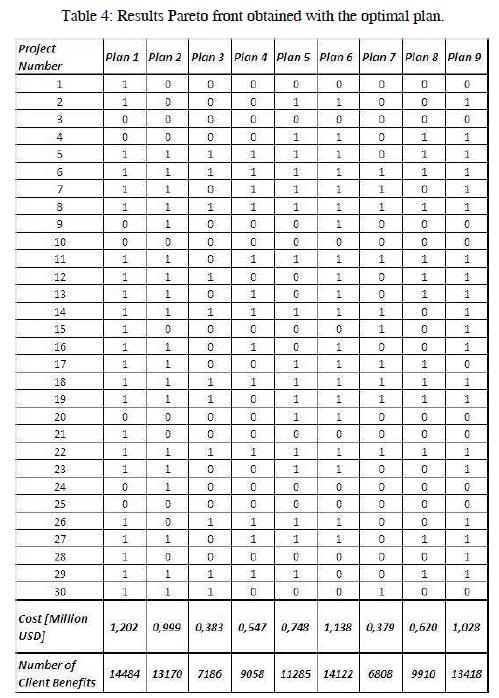
In Figure 6, is plotted the Pareto front achieved by running the algorithm with a mutation of 10% and a population of 150 individuals. These results represent the Pareto optimal front found, however, cannot say that this is the global optimum of the problem, considering that evolutionary algorithms do not guarantee it. Complementary and for examination, Table 4 contains the details of the solutions plotted in Figure 6.
It can be seen that solutions are found costs between 0,333 and 1,2 million USD, and customers benefiting between 6000 and 14500, obviously the number of customers is highly dependent on the impact of projects.
By analyzing carefully the results reflected in Table 4 shows how some projects are included in most plans found in the Pareto front. This is the case of projects 5 to 7, 11, 14, 18, 19, 22 and 29, these have in common the fact that its cost is low and the number of customers benefit is high. Those projects that are not included in some plans within the Pareto front, are characterized, by having a cost / benefit low due to high costs and low impact in terms of customer benefit.
6. Future work
The methodology implemented has a sequential order in terms of optimization, which may be associated with multilevel optimization technique. This approach could be used to solve the planning model holistically, considering the problem of optimal design as the maximum level or leader and the investment planning optimization such as low or subordinate, this raises the possible elements for implementing a technique bi-level, on which work continues.
Moreover, within this work have been seen as objective function the cost of the investment plan and benefit customers. Work continues on the implementation of the algorithms required to optimize other objective functions, depending on the scenario that may arise. Among them may be considered useful for the utilities, optimize plan considering the energy supplied, indicators of quality of service or power quality, among others.
7. Conclusions
In this paper, it has implemented a multi-objective evolutionary algorithm for the investment planning of a distribution system having as objective functions: the cost of the investment plan and the customers benefit.
After presenting the results and discussion highlights the following findings:
The algorithm implemented, it shown as an efficient and useful for decision-making tool, when necessary to define an investment plan to make in a distribution system. With its implementation, is given to the planning expert, sufficient detail and elements to define an investment plan in the short term, whose main objective is the cost benefit to the customer, considering that achieves a positive impact on this power quality.
After exploring different evolutionary operators that affect the performance of the algorithm, it appears that despite these influence the execution time, its effect is negligible, considering that the runtime is running in seconds. However, one must take into account the effect of mutation on the diversity of individuals and the convergence of the algorithm by which, after various tests, we recommend the use of a mutation of 10% and a population 150 individuals, considering that this value yielded the best results.
The implementation of the clustering technique to reduce the external population is beneficial to ensure that individuals of this population to maintain diversity, thus ensuring that it has solutions that adequately represent the Pareto front and not focus on sectors front-specific, since the front is discontinuous due to the characteristics of the problem.
8. References
Bernal-Agustín, J. L. ''Application of genetic algorithms to the optimal design of power distribution systems,'' (in Spanish) Ph.D. dissertation, Dept. Elect.Eng., Univ. Zaragoza, Zaragoza, Spain, 1998. [ Links ]
Boardman, J. T and Meckiff, C. C. ''A branch and bound formulation of an electricity distribution planning problem,'' IEEE Trans. Power App. Syst., vol. 104, pp. 2112-2118, Aug. 1985. [ Links ]
Carreno, E.M.; Moreira, N.; Romero, R.; , "Distribution network reconfiguration using an efficient evolutionary algorithm," Power Engineering Society General Meeting, 2007. IEEE, pp.1-6, 24-28 June 2007. [ Links ]
Coello, C. A; Veldhuizen, D. A. V and Lamont, G. B; Evolutionary Algorithms for Solving Multi-Objective Problems. Springer, Second Edition, MA: Kluwer, 2007. [ Links ]
Coello, C.A., ''Evolutionary Multi-objective Optimization: A Historical View of the Field,'' IEEE Computational Intelligence Magazine, February 2006, pp. 28-36. [ Links ]
CREG Comisión de Regulación de Energía y Gas (CREG); Resolución 097-2008, Por la cual se aprueban los principios generales y la metodología para el establecimiento de los cargos por uso de los Sistemas de Transmisión Regional y Distribución Local. [Online]. Available: http://www.creg.gov.co. [ Links ]
Ferreira, L. A. F. M; Carvalho, P. M. S; Jorge, L.A; Grave, S. N. C and Barruncho, L. M. F; ''Optimal Distribution Planning by Evolutionary Computation How to Make it Work,'' Transmission and Distribution Conference and Exposition (TDCE' 2001), Atlanta, USA, 2001. [ Links ]
Fletcher, R.H. and Strunz, K.; "Optimal Distribution System Horizon Planning-Part I: Formulation," Power Systems, IEEE Transactions, vol.22, no.2, pp.791-799, May 2007. [ Links ]
Gönen.T and Foote, B. L. ''Distribution system planning using mixed integer programming,'' Proc. Inst. Elect. Eng. C, vol. 128, no. 2, pp.70-79, Mar. 1981. [ Links ]
Khator, S. K. and Leung, L. C. ''Power distribution planning: A review of models and issues,'' IEEE Trans. Power Syst., vol. 12, no. 3, pp. 1151- 1159, Aug. 1997. [ Links ]
Khodr, H.M., Vale, Z., Ramos, C., Faria, P., "Optimization techniques for power distribution planning with uncertainties: A comparative study," Power & Energy Society General Meeting, 2009. PES '09.IEEE, pp.1-8, 26-30 July 2009. [ Links ]
Ramirez-Rosado I.J and Dominguez-Navarro, J.A. ''New multi objective tabu search algorithm for fuzzy optimal planning of power distribution systems,'' IEEE Trans. Power Syst., Vol. 21, Issue 1, Pp.224-233, Feb. 2006. [ Links ]
Rivas-Davalos, F., Moreno-Goytia, E., Gutierrez-Alacaraz, G., Tovar-Hernandez, J., "Evolutionary Multi-Objective Optimization in Power Systems: State-of-the-Art," Power Tech, 2007 IEEE Lausanne, pp.20932098, 1-5 July 2007. [ Links ]
RuiXu; Wunsch, D., II;, "Survey of clustering algorithms," Neural Networks, IEEE Transactions on , vol.16, no.3, pp.645-678, May 2005. [ Links ]
Zitzler, E. and Thiele, L., "Multi objective evolutionary algorithms: a comparative case study and the strength Pareto approach," Evolutionary Computation, IEEE Transactions, vol.3, no.4, pp.257-271, Nov 1999. [ Links ]