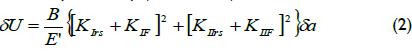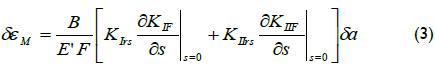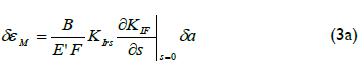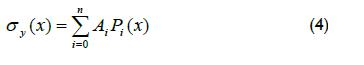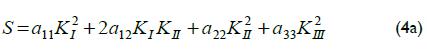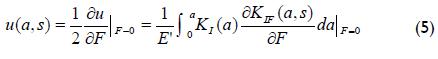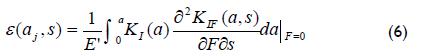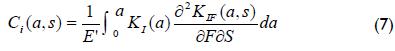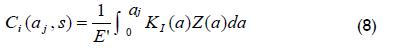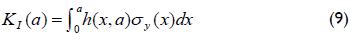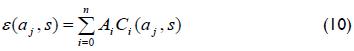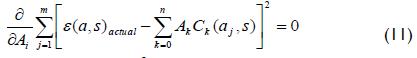Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.32 no.3 Bogotá Dec. 2012
Using fracture mechanics for determining residual stress fields in diverse geometries
Aplicación de la mecánica de la fractura para determinar esfuerzos residuales en diversas geometrías
G. Urriolagoitia-Sosa1, G. Urriolagoitia-Calderón2, B. Romero-Ángeles3, D. Torres-Franco4, L. H. Hernández-Gómez5, A. Molina-Ballinas6, C. R. Torres-San Miguel7 and J. P. Campos-López8
1 Guillermo Urriolagiotia Sosa. Affiliation: ESIME Zatenco del Instituto Politécnico Nacional, Mexico. PhD. In Mechanical engineering, University of Oxford Brookes, United Kindom. E-mail: guiurri@hotmail.com
2 Guillermo Urriolagiotia Calderón. ESIME Zatenco del Instituto Politécnico Nacional, Mexico. PhD. In Mechanical engineering, Imperial college – London, United Kingdom. E-mail: urrio332@hotmail.com
3 Beatriz Romero Ángeles. Affiliation: ESIME Zatenco del Instituto Politécnico Nacional, Mexico. PhD. Candidate, MSc in Mecanical Engineering, ESIME Zatenco del Instituto Politécnico Nacional, Mexico. E-mail: romerobeatriz97@hotmail.com
4 David Torres Franco. Affiliation: ESIME Zatenco del Instituto Politécnico Nacional, Mexico. PhD. candidate, MSc in Mecanical Engineering, ESIME Zatenco del Instituto Politécnico Nacional, Mexico. E-mail: david_torres20@hotmail.com
5 Luis Héctor Hernández Gómez. Affiliation: ESIME Zatenco del Instituto Politécnico Nacional, Mexico. PhD. In Mechanical engineering, University of Oxford, United Kindom. E-mail: luishector56@hotmail.com
6 Arafat Molina Ballinas. Affiliation: ESIME Zatenco del Instituto Politécnico Nacional, Mexico. PhD. candidate, MSc in Engineering manufacture specialty, ESIME Zatenco del Instituto Politécnico Nacional, Mexico. E-mail: yased_83@hotmail.com
7 Christopher René Torres San Miguel. Affiliation: ESIME Zatenco del Instituto Politécnico Nacional, Mexico. DSc. Specialty Mechanical Engineering, ESIME Zatenco del Instituto Politécnico Nacional, Mexico. E-mail: napor@hotmail.com
8 Juan Pablo Campos López. Affiliation: ESIME Zatenco del Instituto Politécnico Nacional, Mexico. PhD. candidate, MSc in Mechanical Engineering, ESIME Zatenco del Instituto Politécnico Nacional, Mexico. E-mail: campos.dono@gmail.com
How to cite: G. Urriolagoitia-Sosa, G. Urriolagoitia-Calderón, B. Romero-Ángeles, D. Torres-Franco, L. H. Hernández-Gómez, A. Molina-Ballinas, C. R. Torres-San Miguel, J. P. Campos-López. (2012). Using fracture mechanics for determining residual stress fields in diverse geometries. Ingeniería e Investigación, Vol. 32, No. 3, pp, 19-26.
ABSTRACT
Component deterioration due to a crack is of the highest importance for the engineering community. Fracture mechanics have mainly been used for studying and evaluating crack or defect nucleation and propagation. This article presents a methodology based on inducing a crack (cut) into mechanical components to characterise an induced residual stress field. This research work's originality was aimed at highlighting fracture mechanics' role in detecting possible component destruction by energetic analysis of crack propagation and evaluating service-life to be used as a technique for characterising the effect of prior loading history regarding a given material. The technique presented in this work is known worldwide as the crack compliance method, based on linear elastic fracture mechanics principles developed by Vaidyanathan and Finnie. Three studies are shown (bent beam, pressurised pipe and modified SEN specimen) where components were induced with a residual stress field. The way non-homogeneous loading could introduce a residual stress field is also presented; if residual stress field acting on a specimen has been characterised, then the mechanical process can be manipulated and a beneficial effect induced into the material.
Keywords: Crack compliance method, residual stress, non-homogeneous loading.
RESUMEN
El deterioro de los componentes debido a falla es un fenómeno que ha recibido constante atención por la comunidad ingenieril. Por su parte, el estudio de la nucleación y propagación de grietas o defectos se analizan principalmente según los principios científicos de la mecánica de la fractura. En este artículo se presenta un método de evaluación desarrollado a partir de la inducción de una grieta (corte) en componentes mecánicos para determinar o caracterizar el campo de esfuerzos residuales actuante. La originalidad de este trabajo resalta en la aplicación de la mecánica de la fractura, que es una ciencia dirigida a detectar la posibilidad de destrucción de un componente mediante el análisis energético de propagación de grietas y evaluación de su vida útil, lo que es utilizado como una técnica para caracterizar el efecto ocasionado por la historia de carga previa en un material. La técnica que aquí se presenta es conocida internacionalmente como método de respuesta de grieta (crack compliance method). Dicho método está fundamentado en principios de mecánica de fractura lineal elástica y fue inicialmente desarrollado por Vaidyanathan y Finnie. En este artículo se presentan tres casos de estudio —viga flexionada, tubo presurizado y probeta SEN modificada— en los cuales los especímenes fueron inducidos con campos de esfuerzos residuales. Asimismo, se presenta la manera como la aplica-ción de cargas no homogéneas introduce un campo de esfuerzos residuales, al conocer la magnitud y características de este campo es posible manipular el proceso mecánico para producir un efecto benéfico en el material.
Palabras clave: Método de respuesta de grieta, esfuerzos residuales, cargas no homogéneas.
Received: December 12th 2011 Accepted: November 2nd 2012
Introduction
For several decades now the scientific community has devoted itself to the task of determining the reasons and way in which components fail; fracture mechanics arose from such need and facilitates analysing component failure in mechanical structures. Failure analysis is aimed at determining how and why mechanical components do not fulfil expected service life when cracking occurs. It has been determined that causes promoting material failure are fatigue, structural overload, wear, corrosion and micro-faults (Urriolagoitia-Calderon et al., 1997; Hernández-Gómez et al., 2009; Gilbert et al., 1994; Lu, James and Roy, 1996). Other variables to be considered would be the type of component application and human factors (O'Connor et al., 2002; Kohn et al., 2010; National Research Council, 1998) such as wrong application and abuse, assembly mistakes, manufacturing faults, inappropriate maintenance, design mistakes, faulty material selection, environmental damage and inadequate thermal treatment. The main objective of failure analysis is to understand the root of the problem regarding cracked components, thereby enabling the prevention of similar cases in the future. Neverthe-less, by now, and based on scientific advances, this article pre-sents the possibility of using fracture mechanics knowledge to determine a material's physical characteristics and the mechanical effects produced by previous loading on components by inducing a crack or cut. Fracture mechanics enables determining the condition of a residual stress field produced by the action of external agents and applying such characterisation facilitates manipulating manufacturing processes to improve a particular material's mechanical properties (Cheng and Finnie, 1990a).
Inducing residual stress in a material is an intrinsic operation caused by fabricating mechanical components, as most manufac-turing processes introduce residual stress into a component. Residual stresses are effects remaining active in a material with-out the action of a load and are the consequence of applying an external non-homogeneous agent exceeding a material's yielding point. Residual stresses are self-equilibrating (tension and compression coexist) and greatly influence a material's mechanical behaviour (Withers and Bhadeshia, 2001; Brinksmeier et al., 1982; Fu et al., 2009). The scientific literature has widely identi-fied such stresses' importance in failure development. Likewise, residual stresses very often cause dimensional instability, once dimensional distortion has been applied after being heat-treated or after machining. The importance of residual stresses is based on the fact that they are produced by all fabrication processes and that they exist in a component regardless of external agent action, thereby being very difficult to determine (Beghini and Bertini, 1990; Ritchie and Leggatt, 1987; Galatolo and Laciotti, 1997; Orkisz and Skrzat, 1996).
Methods for evaluating inducted residual stress fields can be divided into three groups; destructive, semi-destructive and non-destructive. The crack compliance method (CCM) is a destruc-tive method; it has been known by different names such as suc-cessive extension of crack technology, successive cracking method, hollowing method, RUT rectilinear method. Cheng and Fin-nie coined the crack compliance method (CCM) name (Cheng and Finnie, 1988, 1990b and 1994). CCM initiates Schwaighofer's work (1964) which deserves mention as being the first to use a groove to measure residual stress. In fact, two grooves were manufactured into a component and residual stress field determined using strain gauges. The CCM as we know it was devel-oped by Vaidyanathan and Finnie (1971); they measured the residual stress field acting on a plate welded end, by introducing a hole and then extending the groove from the hole using a jeweller's saw. Then, for every increase in groove length, stress intensity factor KI was determined by applying photo-elastic technology. Inverse technology was applied to find a solution near the residual stress field acting on the component. Techno-logical advances by the mid-1980s stimulated investigation to use the CCM. This research trend continued in later years (Prime, 1999) in:
- the USA (Cheng and Finnie, 1988, 1990a, 1990b and 1994, Prime, 1999 and 2000);
- Holland (Ritchie and Leggatt, 1987);
- the UK (Ritchie and Leggatt 1987; Nowell, Tochilin and Hills, 2000; Reid, 1988; Urriolagoitia-Sosa, Durodola and Fellows 2007);
- Germany (Fett and Thun, 1996);
- South Korea (Kang, Song and Earmme, 1989);
- Mexico (Urriolagoitia-Sosa, 2005; Urriolagoitia-Sosa et al., 2007 and 2009);
- Switzerland (Schindler and Landolt, 1997; Schindler and Bertsschinger, 1997);
- Italy (Galatolo and Laciotti, 1997);
- Poland (Orkisz and Skrzat, 1996); and
- China (Oh, Lai and Nee, 1993; Lai and Siew, 1995).
Most CCM applications have involved using common metals (high, medium and low carbon steel, stainless steel, bio-compatible metals, aluminium alloy, etc) (Prime, 2000; Jones and Dunn, 2008; Nervi et al., 2009). Research by Fett and Thun (1996) involved using PMMA and PVC whereas Herman (1995) successfully applied CCM in materials having a metal matrix.
This paper analyses how inducing a cut (crack) into a mechanical component can be used to characterise the residual stress field acting on a component. Three experimental study cases are analysed: a bending beam (without and with previous loading history), a pipeline subjected to service pressurised conditions and a modified SEN specimen used for crack arrest analysis. Inducing a residual stress field in each specimen altered the ma-terials' mechanical resistance and consequently modified a component's mechanical characteristics. It also describes the manner in which non-homogeneous loads are applied to introduce a specific residual stress field for every case and how a mechanical process might be manipulated to produce a beneficial effect in a particular material (Peyre et al., 2000; Kudryavtsev, 2008; John, Jata and Sadananda, 2003). A residual stress field's beneficial aspect can only be induced if external agent application magni-tude and form is known and the field characterised, so that the effect of an external agent can be modified or some other external agent added to generate an expected beneficial effect.
The crack compliance method's theoretical ba-sis (Urriolagoitia-Sosa, 2005)
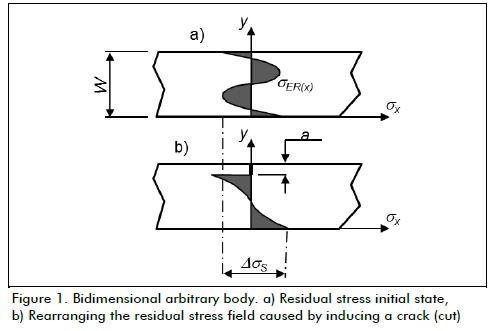
This methodology was developed by Vaidyanathan and Finnie in 1971 and afforded the possibility of an acting residual stress field being obtained in a mechanical component by means of the stress intensity factor when a crack was introduced into a given material (Prime, 1999). A crack can be induced by producing an initial cut, making it extend slowly in a controlled way; nevertheless, cases have been detected where a cut induced cold has altered the original residual stress field acting on a component. It was thus proposed to make a cut by means of electro-erosion technology and thus eliminate this problem. When a cut is made in a material presenting a residual stress field, there is partial relaxation of such residual stress field due to stress rearrangement in the body causing deformation (Figure 1). Deformation by inducing a cut can be determined by using strain gauges. Such cut would eventually transform a residual stress field originally acting on material, so deformation produced by relaxation effects is used by the CCM to determine the residual stress field in a given material. A residual stress field from deformation or strain produced by relaxation can be determined in two ways: direct solu-tion and/or inverse solution method (Prime, 1999). Both tech-niques are based on linear elastic fracture mechanics principles. An inverse solution is described.
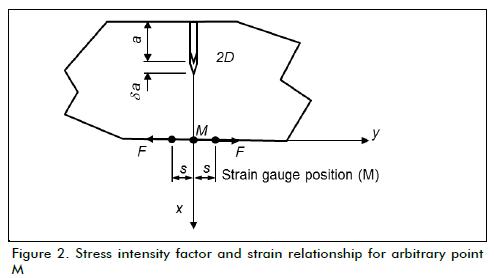
Consider a bi-dimensional arbitrary body suffering the effect of longitudinal cracking "α" and a residual stress field (Figure 2). When the crack length is extended by a small increase δa, a strain change at the surface of the body δεM, takes place. This can be expressed by Castigliano's theorem (Todd, 1981) as:
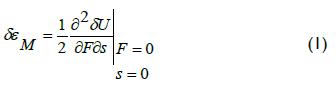
where δU is elastic energy in a component stored before and after crack extension, F is an acting virtual force and s is the distance from arbitrary point M. The elastic energy difference, in terms of stress intensity factor, present before and after crack extension is expressed by (Irwin, 1957):
E´ is the generalized Young's modulus (E' = E for plane stress condition and E' = E/(1-v 2) for plane strain condition), B is the thickness of the body. At the crack tip KIrs and KIIrs are stress intensity factors caused by residual stress field, KIF and KIIF are the stress intensity factors due to applying a virtual force. Substituting Equation 2 in Equation 1 and as KIF is a linear function depending on F and KIrs is independent of s (Schindler and Landolt, 1997), would give:
This work considered that they did not exist for system KIIF and KIIrs ( because it was a symmetrical system regarding the crack plane, and the forces did not lead to shear stress in plane y = 0) (Schindle and Bertsschinger, 1997), so:
The ratio between strain change at M and stress intensity factor for each crack increase could be By obtained by applying Equation 3a, expressed as (Schindle and Bertsschinger, 1997):
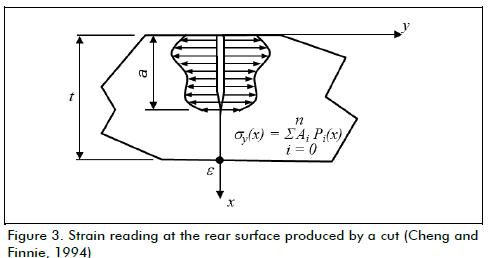
where Z(a) is a function depending on component geometry. The overall inverse polynomial method can be developed from here for determining the residual stress field acting on a component (Urriolagoitia-Sosa, 2005). Consider crack a with length t and unitary body thickness (Figure 3) (Irwin, 1957).
Stress function σy(x) is unknown, so it has to be determined by using strain measurements ε, at the point where a crack will pass (x = 0, y = s o x = t, y = 0) (Figure 3). The unknown residual stress distribution in the beam can be represented by adding an nth order polynomial series as (Cheng and Finnie, 1994):
where Ai is the coefficient to be obtained and Pi a power series, x0, x1, x2, …. xn etc. Legendre polynomials are also used. Howev-er, the CCM includes a step which assumes that stress distribu-tion, σy(x) = Pi(x), interacting with the crack is known. This known stress field is used to obtain crack compliance function C by using Castigliano's approach. The change in strain energy due to the presence of the crack and the virtual force must thus be evaluated. Strain energy density represents one alternative; its main factor, S, is direction sensitive. It establishes the direction of least resistance for crack initiation. The stationary value of Smin can be used as an intrinsic material parameter whose value at the point of crack instability is independent of crack geometry and loading. The expression for the intensity of the strain energy density field for an elastic material would be:
This criterion is based on energy field local density at the crack tip and does not require any assumption regarding the direction in which energy is released. This is suitable for mixed mode loading. For the problem at hand, KI = σa112; KII = KIII = 0, because the specimen was under mode I. S could thus be combined with Castigliano's theorem. Displacement u(a,s) could be determined by taking a derivative regarding virtual force, as (Cheng and Finnie, 1994):
Differentiating now regarding distance s, strain in x-direction was given by (Cheng and Finnie, 1994):
Strain ε(a,s) (where a = crack length and s the distance between location of strain gauge and crack plane) due to stress fields Pi(x) is known as the compliance function Ci(aj,s) and is given by:
Due to KIF linearity with F, the second term under the integral sign in Equation 7 would be the same as Z(a) in:
By following the procedure developed by Schindler et al., (1994) and Kang et al., (1989) for a beam with strain measurement data at point M, KI(a) can be expressed as:
where σy(x) = Pi(x) and h(x,a) is known as the weight function. Once Ci(a,s) is determined, the strain due to the stress in a com-ponent can be calculated by (Cheng and Finnie, 1994):
Unknown terms Ai were determined so that the strain given by Equation 10 matched those measured in the experiment during cutting, i.e. ε(aj,s)actual. To minimise average error over all data points for nth order approximation, the least squares method was used to obtain values for Ai. Therefore the number of cutting increases m was chosen to be greater than the order of the polynomial, i.e. m > n. This work used n = 7 with 8 constants Ai and m = 9, this being the number of experimental slot cutting depths at which strain readings were collected. The least squares solution was obtained by minimising the square of the error relative to unknown constant Ai (Cheng and Finnie, 1994):
So:
This gave [H]{A}={J} where [H]=[C]T[C] and {J}=[C]T{εj}actual (Ur-riolagoitia-Sosa, 2005, Urriolagoitia-Sosa et al., 2007) giving a linear set of simultaneous solutions from which Ai values were determined and Equation 4 was then used to determine residual stress distribution. A FORTRAN program was used for numerical procedure.
Finite element numerical simulation method
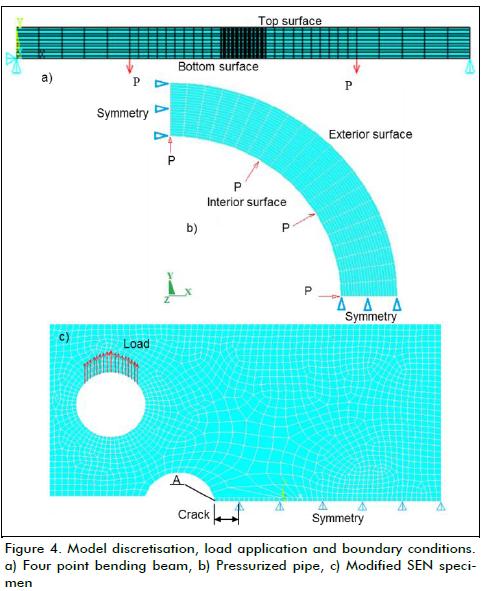
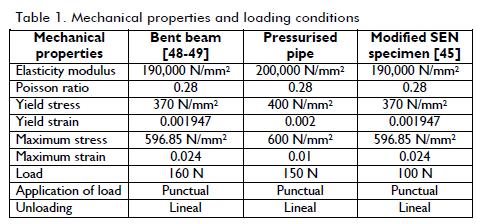
Numerical simulations were developed for each case studied in this work. All numerical analysis was carried out using commercial computational software and the finite element method (FEM), involving structural evaluation, two-dimensional modelling and plane stress theory. An 8-node solid-plane element was used for each numerical study, considering three degrees of freedom (x, and y, rotation in z). Numerical evaluations involved elasto-plastic considerations and a kinematic hardening rule (Urriolago-itia-Sosa, 2005). The model's geometry was developed and the model discretised in a controlled manner, preserving mesh homogeneity (Figure 4). The mechanical properties and external agents in each case study are presented in Table 1. The results are given after the system was unloaded.
It should be mentioned that two numerical analyses were per-formed for the modified SEN specimen, applying the previous considerations. The first study involved an evaluation of the residual stress field considering geometry having a stress concentrator; the effect caused by inducing a 5 mm length cut on introducing a residual stress field was added in the second case (Romero-Ángeles, 2009).
Experimental development
This work involved experimental investigation including three study cases: a bent beam under pure flexion (with and without previous loading history) (Kang et al., 1989; Urriolagoitia-Sosa et al., 2003; Urriolagoitia-Sosa, 2005), a previously pressurised pipe (Cheng and Finnie, 1986) and a modified SEN specimen (Romero-Ángeles, 2009; Urriolagoitia-Sosa et al., 2010a and b). The residual stress field induced in each component was deter-mined for quantifying its effect on the material's mechanical resistance and to propose (if possible) a mechanical process for improving a component's physical characteristics or to define the magnitude of damage resulting from action which could take place in a specimen. For each case of CCM application, a cut was introduced by using an electro-erosion machine with copper plate electrode and considering that supporting the piece was freely relaxed to obtain the strain information.
Bent beam (with and without previous loading history)
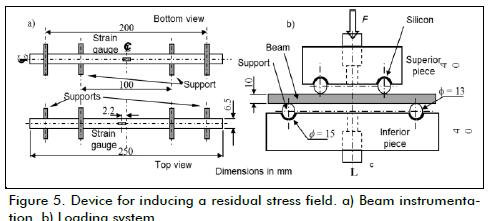
Stainless steel alloy AISI 316L was used to induce a residual stress field by pure flexion in a beam (Molina-Ballinas, 2010; Urriolagoitia-Sosa et al., 2010c). The material consisted of trans-verse rectangular section bars (10 mm height and 6.35 mm base). 12 equal specimens were cut to 250 mm length and were partial-ly annealed at 600oC for 30 minutes in an electric oven and were left inside the oven to slowly cool down (Molina Ballinas, 2010). The intention of annealing the material before introducing the residual stress field was to eliminate any previous loading history preserving the effect of the residual stress field induced in a controlled manner. All beams were instrumented with strain gauges on top and bottom surfaces (Figure 5a). The bottom strain gauge was then used for CCM. The batch of specimens was separated into two groups of 6 units each. The first group of beams was induced with a residual stress field by pure bending using a servo-hydraulic machine (Figure 5b). The second group of specimens was pre-loaded with homogeneous compressive load before inducing the residual stress field by pure bending. The previous loading history applied by the axial compressive load modified the axisymmetric distribution of the residual stress field induced by the bending procedure; regarding the case lacking previous history, this operation increased the component's mechanical resistance (Urriolagoitia-Sosa et al., 2010c). The second case involved a compressive axial load being applied until the strain gauge reached 13,300 µε (beyond yield strain). All specimens from both groups were bent by an INSTRON ma-chine with a 2.5 kN recorded load. This load was big enough to exceed the material's yielding point (for both groups), thus in-ducing a residual stress field in each specimen.
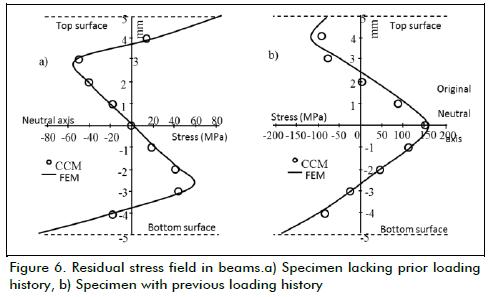
Once the residual stress field had been induced, the strain gauge on the bottom of the beam was sealed with silicon. The gauge was sealed as protection, since electro-erosion machine cutting needs a specimen to be immersed in a container containing dielectric liquid. A progressive 1 mm length cut was made begin-ning at the top surface; this cut was aimed at producing rear-rangement of the residual stress field and producing a deformation effect. The cut length was verified at the end of each process and the strain value caused by the relaxation was rec-orded; 9 cuts were made from the top surface of the beam to the bottom surface in every specimen, keeping a 1 mm length of material intact to preserve structural integrity (Molina-Ballinas, 2010; Urriolagoitia-Sosa et al., 2010c). The relaxation produced by 9 cuts was used for determining the original residual stress field using CCM. Figure 6a shows the residual stress field for a beam lacking prior loading history and subjected to pure bending. Figure 6b shows the residual stress field in a beam with harden-ing surface by compression and pure bending. The results shown in Figures 6a and 6b (considering the location of the neutral axis in the centre of the beam's height) led to observing the change in residual stress field axisymmetric distribution for previous load-ing history. Results obtained from FEM (Urriolagoitia-Sosa, 2005; Molina-Ballinas, 2010; Urriolagoitia-Sosa et al., 2010c), shown in Figure 6 for both cases (with and without loading history) vali-dated the CCM.
Pressurised pipe
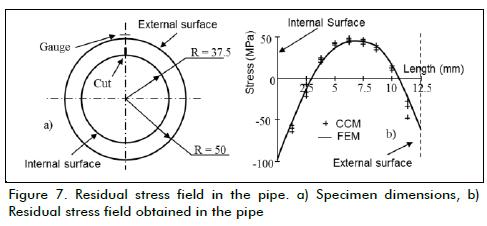
The second analysis involved a sample of X42Cr13 steel pipe; this type of metal is mainly used in the petroleum industry (Figure 7a). A section of this pipe was obtained which had been used in service conditions for transporting petrochemical fluid.
Even though the effects of service condition could not be fully determined, it was thought that internal fluid pressure in the pipe could have induced a residual stress field. The pipe sample was cut to obtain 15 mm thickness specimens having ring geometry. Three specimens were instrumented with strain gauges (Figure 7a) and an electro-erosion cut was made. Twelve specimens were tested, each having a 1 mm length cut, and t strain relaxa-tion was recorded at the end of each test. The CCM could be used with the strain data obtained for determining the residual stress field acting in the pipe (Figure 7b). Likewise, results obtained by the FEM validated the CCM.
Modified SEN specimen
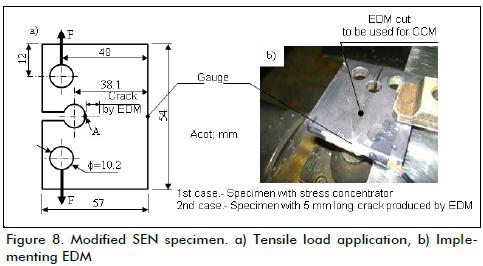
The effect caused by a residual stress field in a component having stress concentration and then inducing a residual stress field produced cracked component behaviour. A modified SEN specimen was used for experimental analysis (Figure 8a).
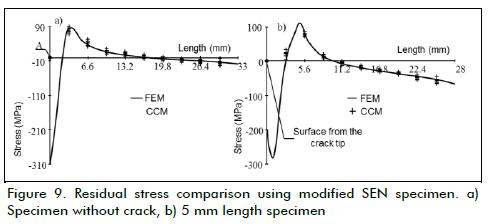
AISI 316L stainless steel was selected for this research. The specimens were manufactured from 6.35 mm thick plate and a batch of 12 specimens was prepared. The material was annealed at 600oC for 30 minutes in an electric oven and left inside to cool down slowly (Romero-Ángeles, 2009; Urriolagoitia-Sosa et al., 2010a and 2010b). The specimens were separated into two groups of 6 units each. The first group was induced with a resid-ual stress field by applying a tensile load in a servo-hydraulic machine. Tensile load was 10.5 kN (Figure 8a). The second group of specimens was prepared by introducing a 5 mm crack (Figure 8b) by electro-erosion (EDM). A residual stress field was then induced in the specimens by applying a tensile load having the same magnitude as the previous case. All specimens were instrumented with strain gauges on one of the specimens' lateral faces. The strain gauge was used (after introducing the cut (crack)) to collect data using the CCM to determine the residual stress field acting on a specimen. 1 mm deep cuts were made (depending on the specimen, from the main stress concentration point (A in Figure 8a) or the crack tip). The cut was made up to 1 mm before reaching a specimen's lateral surface and preserving some structural integrity. Figure 9a shows the residual stress field obtained by experimental procedure in modified SEN spec-imens without a previous crack; Figure 9b shows the residual stress field in the modified SEN specimen with a previously in-duced 5 mm length crack, taking the crack tip as the beginning of the cut for using CCM. These two figures also give the FEM numerical simulation results.
Discussion and Conclusions
The appearance of cracks in mechanical components has produced great interest for a long time now due to mechanical system deterioration, economic expense and possible human loss. Mankind has developed many means of combating the effects of deterioration causde by component cracking. It is evident that technologies strengthening a cracked component involve manipulating their physical properties by means of mechanical processes (Hahn and Kanninen, 1980). As such, inducing residual stress fields is of the utmost importance as this can strengthen a material's resistance, promoting no failure nucleation and delaying crack propagation (Green, Tandon and Sglavo, 1999). Never-theless, residual stresses are self-equilibrated (as tensile and compressive stress coexists) making their application and measurement an extremely difficult issue.
This paper has analysed the results of three study cases where residual stress fields were induced. Even though such cases were only theoretical, they ascertained manipulating mechanical processes for inducing a beneficial residual stress field for strengthening a material's mechanical behaviour. They were diverse as were the mechanical processes which would propitiate beneficial residual stress field in a particular component.
Figure 6a shows that an axisymmetric residual stress field was induced in bent beams, even though the benefits this kind of field could bring to the material could not be determined. When beams having characteristics such as those in the previous study were submitted to strain hardening by applying an axial compressive load, it could be observed (Figure 6b) how the residual stress field lost its axisymmetry and a large area had compressive stress on both component surfaces. It may be concluded that compressive residual stress tended to reduce crack propagation probability (Löhe, Lang and Vöhringer, 2002), since the tensile effect (causing a material's deterioration) would have to over-come the compression effect induced by the stress field. It could also be observed that the tensile area became reduced, meaning that the mechanical process applied in experimental analysis was beneficial for a component's service life (Urriolagoitia-Sosa, 2005). Experimental analysis was validated by the FEM (Urriola-goitia-Sosa, 2005).
The service effect acting on a riser by inducing a residual stress field was determined in the second study case, considered to be fatigue set up in the mechanical component. CCM led to determining residual stress field distribution and magnitude and the possible benefit from inducing residual compressive stress on the pipe's surface. It is worth mentioning that tensile residual stress-es are located at the centre of a specimen and may not be considered as detrimental since cracks usually nucleate and propagate from the surface of an element. Figure 7b clearly shows the compressive residual stress field present on the pipe's transverse surface plane; this could have prevented crack nucleation and its possible propagation. Such compressive residual stress field could also be found on the pipe's internal surface within the component's fatigued area, having greater magnitude than that on the external surface. Fatigue when removing the pipe was most probably strengthening both surfaces. Nevertheless, it was obvious that the fatigue effect of major service cycles would eventually damage the material and cause the pipe to fail. Once again, numerical analysis simulated the pipe's working conditions to validate this research.
Analysis focused on two considerations for a modified SEN specimen in the last case study to visualise the positive effects obtained by strain hardening when an applied load exceeded the material's yielding point, followed by removing the load. This was done on two types of specimen: one with stress concentration and one where a crack was introduced. Compressive residual stress was generated in both cases at the surface near point A and the crack tip. Figures 9a and 9b show the material's in-creased mechanical resistance in both cases. Such increased mechanical resistance was due to the compressive residual stress field, indicating that the component's tensile reloading had first to pass over the compressive stress to produce tensile stress and damage. This implied that the element could support a major tensile effect before cracking would occur. Nevertheless, such geometry and study case need to be extensively analysed, since a crack and possible propagation increases risk when applying the component (Molina-Ballinas, 2010; Urriolagoitia-Sosa et al., 2010c; Brandes, 1992).
This work has proposed a methodology for mechanically manipu-lating materials' properties and geometry to strengthen resistance to cracking or damage. The crack compliance method's versatility and accuracy has also been demonstrated for determining residual stress fields, as well as its low cost and ease of application.
Acknowledgments
The authors gratefully acknowledge financial support provided by the Mexican government via the Consejo Nacional de Ciencia y Tecnología, Instituto de Ciencia y Tecnología del D. F. and the Instituto Politécnico Nacional. Technical support was also provided by José Alfredo Rangel Hernández and Luis Miguel López Hernández.
Variables

References
Beghini, M., Bertini, L., Residual stress modeling by experimental measurements and finite element analysis., Journal of Strain Analysis for Engineering Design, Vol. 25, No. 2, 1990, pp. 103-108. [ Links ]
Brandes, E.A., Brook, G.B., (ed.), Smithells Metals Reference Book., 7th ed., USA, Butterworth Heinemann, 1992, pp. 22.1-22.27. [ Links ]
Brinksmeier, E., Cammett, J.T., König, W., Leskovar, P., Peters, J., Tönshoff, H.K., Residual stresses; Measurement and causes in machining processes., CIRP Annals-Manufacturing Technology, Vol. 31, No. 2, 1982, pp. 491-510. [ Links ]
Cheng, W., Finnie, I., Measurement of residual hoop stress in cylinders using the compliance method., Journal of Engineering Material and Technology, Vol. 108, 1986, pp. 87-92. [ Links ]
Cheng, W., Finnie, I., KI solutions for an edge cracked strip., Engineering Fracture Mechanics, Vol. 31, No. 2, 1988, pp. 201-207. [ Links ]
Cheng, W., Finnie, I., The Crack Compliance Method for Residual Stresses Measurement., Welding in the World, Vol. 28, 1990a, pp. 103-110. [ Links ]
Cheng, W., Finnie, I., A KII stress intensity solution for an edge cracked strip., Engineering Fracture Mechanics, Vol. 36, No. 2, 1990b, pp. 355-360. [ Links ]
Cheng, W., Finnie, I., An overview of the crack compliance method for residual stress measurement., Proceedings Fourth International Conference on Residual Stress, Baltimore, Maryland, Society for Experimental Mechanics, 1994, pp. 449-458. [ Links ]
Fett, T., Thun, G., Residual stresses in PVC-cylinders determined with the weight function method., Journal of Engineering Fracture Mechanics, Vol. 55, No. 5, 1996, pp. 859-863. [ Links ]
Fu, W.E., Cohen, P.H., Ruud, C.O., Experimental investigation of the machining induced residual stress tensor under mechanical loading., Journal of Manufacturing Processes, Vol. 11, No. 2, 2009, pp. 88-96. [ Links ]
Galatolo, R., Laciotti, A., Fatigue crack propagation in residual stress fields of welded plates., International Journal of Fatigue, Vol. 19, No. 1, 1997, pp. 43-49. [ Links ]
Gilbert, J.L., Buckley, C.A., Jacobs, J.J., Bertin, K.C., Zernich, M.R., Intergranular corrosion-fatigue failure of Cobaltalloy femoral stems; A failure analysis of two implants., Journal of Bone and Joint Surgery, Vol. 76, No. 1, 1994, pp. 110-115. [ Links ]
Green, D.J., Tandon, R., Sglavo, M.V., Crack arrest and multiple cracking in glass through the use of designed residual stress profiles., Science, Vol. 283, No. 5406, 1999, pp. 1295-1297. [ Links ]
Hahn, G.T., Kanninen, M.F., (ed.), Crack Arrest Methodology and Applications., American Society for Testing and Materials, 1980. [ Links ]
Hermann, R., Crack growth and residuals stress in Al-Li metal matrix composites under far-field cyclic compression., Journal of Material Science, Vol. 30, 1995, pp. 3782-3790. [ Links ]
Hernández-Gómez, L.H., Urriolagoitia-Calderón, G., Urriolagoitia-Sosa, G., Sandoval-Pineda, J.M., Merchán-Cruz, E.A., Guardado-García, J.F., Assessment of the structural integrity of cracked cylindrical geometries applying the EVTUBAG program., Revista Técnica de Ingeniería de la Universidad de Zulia, Vol. 32, No. 3, 2009, pp. 190-199. [ Links ]
Irwin, G.R., Analysis of stresses and strains near the end of a crack traversing a plate., Journal of Applied Mechanics, Vol. 24, 1957, pp. 361-363. [ Links ]
John, R., Jata, K.V., Sadananda, K., Residual stress effects on near-threshold fatigue crack growth in friction stir welds in aero-space alloys., International Journal of Fatigue, Vol. 25, No. 9-11, 2003, pp. 939-948. [ Links ]
Jones, K.W., Dunn, M.L., Fatigue crack growth through a residual stress field introduced by plastic beam bending., Journal of Fatigue and Fracture of Engineering Materials and Structures, Vol. 31, No. 10, 2008, pp. 863-875. [ Links ]
Kang, K.J., Song, J.H., Earmme, Y.Y., A method for the measurement of residual stresses using a fracture mechanics approach., Journal Strain Analysis for Mechanical Design, Vol. 24, 1989, pp. 23-30. [ Links ]
Kohn, L.T., Corrigan, J., Donalson, M.S., (ed.), To Err is Human; Building a Safer Health System., USA, Institute of Medicine; Committee on Quality of Health Care in America, 2010, pp. 63-65. [ Links ]
Kudryavtsev, Y.F., Residual Stress, Springer Handbook of Experimental Solid Mechanics, W.N. Sharpe Jr., (ed.), Springer SEM, 2008, pp. 371-386. [ Links ]
Lai, M.O., Siew, Y.H., Fatigue properties of cold worked holes., Journal of Materials Processing Technology, Vol. 48, 1995, pp. 533-540. [ Links ]
Löhe, D., Lang, K.H., Vöhringer, O., (ed.), Residual stress and fatigue behavior., Handbook of Residual Stress and Deformation of Steel, USA, ASM International, 2002, pp. 27-53. [ Links ]
Lu, J., James, M., Roy, G., (ed.), Handbook of Measurements of Residual Stress., USA, Fairmont Press, Inc., 1996. [ Links ]
Molina-Ballinas, A., Evaluación y determinación experimental-numérica del endurecimiento por deformación y el efecto Bauschinger en las propiedades mecánicas de un acero inoxidable., MSc thesis SEPI-ESIME, Instituto Politécnico Nacional, México, 2010. [ Links ]
National Research Council, (ed.), Improving the Continued Air-worthiness of Civil Aircraft; A Strategy for the FAA´S Aircraft Certification Service., USA, National Academy Press, 1998, pp. 24. [ Links ]
Nervi, S., Szabó, B.A., Young, K.A., Prediction of distortion of air-frame components made from aluminum plates., AIAA Journal, Vol. 47, No. 7, 2009, pp. 1635-1641. [ Links ]
Nowell, D., Tochilin, S., Hills, D. A., Measurement of residual stress in beams and plates using the crack compliance technique., Journal Strain Analysis for Mechanical Design, Vol. 35, No. 4, 2000, pp. 277-285. [ Links ]
O´Connor, P.D.T., Newton, D., Bromley, R., (ed.), Practical Reliability Engineering., 4a ed., England, John Wiley and Sons, Inc., 2002, pp. 1-20. [ Links ]
Oh, J.T., Lai, M.O., Nee, A.Y.C., Stress analysis of a ballised hole., Journal of Materials Processing Technology, Vol. 37, 1993, pp. 137-147. [ Links ]
Orkisz, J., Skrzat, A., Reconstruction of residual stresses in railroad vehicle wheels based on enhanced saw cut measurements; Formulation and benchmark tests., Wear, Vol. 191, 1996, pp. 188-198. [ Links ]
Peyre, P., Scherpereel, X., Berthe, L., Carboni, C., Fabbro, R., Béranger, G., Lamaitre, C., Surface modifications induced in 316L steel by laser peening and shot-peening; Influence on pitting corrosion resistance., Materials Science and Engineering A, Vol. 280, No. 2, 2000, pp. 294-302. [ Links ]
Prime, M.B., Residual stress measurement by successive extension of a slot; The crack compliance method., Applied Mechanics Reviews, Vol. 52, No. 2, 1999, pp. 75-96. [ Links ]
Prime, M.B., Prantil, V.C., Rangaswamy, P., Garcia, F.P., Residual stress measurement and prediction in a hardened steel ring., Materials Science Forum, Vols. 347-349, 2000, pp. 223-228. [ Links ]
Reid, C.N., A method of mapping residual stress in a compact tension specimen., Scripta Metallurgica, Vol. 22, No. 4, 1988, pp. 451-456. [ Links ]
Ritchie, D., Leggatt, R.H., The measurement of the distribution of residual stress through the thickness of a welded joint., Strain, Vol. 23, No. 2, 1987, pp. 61-70. [ Links ]
Romero-Ángeles, B., Aplicación de multicargas para el arresto de grietas., MSc thesis, SEPI-ESIME, Instituto Politécnico Nacional, México, 2009. [ Links ]
Schindler, H.J., Bertsschinger, P., Some steps towards automation of the Crack Compliance Method to measure residual stress distribution., 5th International Conference on Residual Stresses, Sweden, 1997, pp. 682-687. [ Links ]
Schindler, H.J., Cheng, W., Finnie, I., Measurement of the residual stress distribution in a disk or cylinder using the crack compliance method., Proceedings Fourth International Conference on Residual Stress, Baltimore, Maryland, Society for Experimental Mechanics, 1994, pp. 1266-1274. [ Links ]
Schindler, H.J., Landolt, R., Experimental determination of residual stress and the resulting stress intensity factors in rectangular plates., 4th European Conference on Residual Stresses (ECRS4), Cluny, France, 1997, pp. 509-517. [ Links ]
Schwaighofer, J., Determination of residual stresses on the surface of structural parts., Experimental Mechanics, Vol. 4, No. 2, 1964, pp. 54-56. [ Links ]
Todd, J.D., (ed.), Structural Integrity and Analysis., 2a ed., USA, McMillan Publishers, Ltd., 1981, pp. 181-189. [ Links ]
Urriolagoitia-Calderón, G., Hernández-Gómez, L.H., Villa y Rabasa, G., Urriolagoitia-Sosa, G., Medina-Velarde, J.L., Vázquez-Mendoza, H.H., León-Vega, C., Solución conceptual del comportamiento de una probeta agrietada sometida a cargas de fatiga para determinar su vida remanente., Científica, Año 1, No. 5, Sep.-Oct., 1997, pp. 39-42. [ Links ]
Urriolagoitia-Sosa, G., Analysis of prior strain history effect on mechanical properties and residual stresses in beams., PhD thesis presented at the University of Oxford Brookes, Oxford, Inglaterra, 2005. [ Links ]
Urriolagoitia-Sosa, G., Durodola, J.F., Fellows, N.A., Determination of residual stress in beams under Bauschinger effect using surface strain measurements., Strain, Vol. 39, No. 4, 2003, pp. 177-185. [ Links ]
Urriolagoitia-Sosa, G., Durodola, J.F., Fellows, N.A., Effect of strain hardening on residual stress distribution in beams determined using the crack compliance method., Journal Strain Analysis for Mechanical Design, Vol. 42, No. 2, 2007, pp. 115-121. [ Links ]
Urriolagoita-Sosa, G., Romero-Ángeles, B., Hernández-Gómez, L.H., Urriolagoita-Calderón, G., Beltrán-Fernández, J.A., Torres-Torres, C., Evaluation of the impact of residual stresses in crack initiation with the application of the Crack Compliance Method; Part I, Numerical analysis., Applied Mechanics and Materials, Vol. 24-25, 2010a, pp. 253-259. [ Links ]
Urriolagoita-Sosa, G., Romero-Ángeles, B., Hernández-Gómez, L.H., Urriolagoita-Calderón, G., Beltrán-Fernández, J.A., Torres-Torres, C., Evaluation of the impact of residual stresses in crack initiation with the application of the Crack Compliance Method; Part II, Experimental analysis., Applied Mechanics and Materials, Vol. 24-25, 2010b, pp. 261-266. [ Links ]
Urriolagoita-Sosa, G., Molina-Ballina, A., Urriolagoitia-Calderón, G., Hernández-Gómez, L.H., Sandoval-Pineda, J.M., Characterization of strain hardening behavior and residual stress induction used for crack arrest in a biocompatible material., Material Research Society, Vol. 1242, 2010c, pp. 233-239. [ Links ]
Urriolagoitia-Sosa, G., Sandoval-Pineda, J.M., Merchán-Cruz, E.A., Rodríguez-Cañizo, R.G., Urriolagoitia-Calderón, G., Hernández-Gómez, L.H., Rodríguez-Martínez, R., Torres-Martínez, R., Experimental application of the Crack Compliance Method in beams with hardened surfaces., Revista Mexicana de Física, Vol. 55, No. 1, 2009, pp. 30-33. [ Links ]
Vaidyanathan, S., Finnie, I., Determination of residual stresses from stress intensity factor measurements., Journal of Basic Engineering, Vol. 93, 1971, pp. 242-246. [ Links ]
Withers, P.J., Bhadeshia, H.K.D.H., Residual stress; Part 1-Measurement techniques., Journal of Materials Science and Technology, Vol. 17, No. 4, 2001, pp. 355-365. [ Links ]