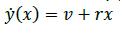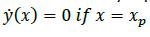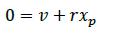Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.32 no.3 Bogotá Dec. 2012
A study of shallow water's effect on a ship's pivot point
Estudio de efectos por aguas someras sobre el punto de pivote de un buque
J. E. Carreño1, J. D. Mora2, F. L. Pérez3
1 Jorge Enrique Carreño. Affiliation: Almirante Padilla Naval School. PhD. in Naval Engineering, Universidad Politécnica de Madrid. E-mail: denap@enap.edu.co
2 Jaime David Mora. Affiliation: COTECMAR., MSc. in Mechanical Engineering, Universidad Nacional de Colombia. E-mail: jmora@cotecmar.com
3 Francisco Lázaro Pérez. Affiliation: Universidad Politécnica de Madrid. PhD. in Naval Engineering, Universidad Politécnica de Madrid. E-mail: francisco.perez.arribas @upm.es
How to cite: J. E. Carreño, J. D. Mora, F. L. Pérez (2012). A study of shallow water's effect on a ship's pivot point. Ingeniería e Investigación. Vol. 32, No. 3. December 2012, pp. 27-31.
ABSTRACT
Information regarding a turning ship's pivot point has been collected, taking practical notes and ship maneuvering manuals into account as well as experimental data and simulated results, together revealing consistent behaviour when varying water depth or some ship's particulars. Results from studies already carried out using the Colombian Navy's River Support Patrol Vessel (RSPV) are included here to estimate the pivot point and contrast results with theory and available observations. Linear manoeuvrability theory was tested and the results revealed poor agreement with kinematic equations. As to the depth variation effect, full-scale experiments confirmed that the pivot point's position, when in shallow water, always varied in the same way, thereby agreeing with available pivot point information.
Keywords: Pivot point, shallow water, manoeuvrability.
RESUMEN
Se recopila información relacionada con el punto de pivote (o punto de giro) del buque durante un giro, teniendo en cuenta información derivada de notas y manuales prácticos de maniobra de buques, así como datos experimentales y numéricos que en conclusión dejan ver un comportamiento consistente al variar la profundidad del agua o algunas características del buque. Los estudios sobre un buque en particular, la nodriza o patrulla de apoyo fluvial pesada (PAF-P) son incluidos en este, con el fin de estimar el punto de pivote y confrontar los resultados con las teorías y observaciones empíricas documentadas. La teoría de maniobrabilidad lineal es probada y los resultados revelan una aproximación muy pobre con respecto a las fórmulas puramente cinemáticas. En cuanto al efecto de la profundidad, se comprueba con experimentación a escala real que la posición del punto de pivo-te, al pasar a aguas someras, varía siempre en el mismo sentido y es coherente con la información disponible de este fenómeno.
Palabras clave: Punto de pivote, aguas someras, maniobrabilidad.
Received: March 13th 2011 Accepted: November 20th 2012
Introduction
The pivot point (PP) is a non-fixed point on a ship's axis of symmetry and has no sideways motion while a ship is turning, i.e. it is the position on the symmetry axis having zero drift angle (Tzeng, 1998; Port Revel, 2011). According to Cauvier (2008), a more accurate name should be "apparent pivot point". Such point may be taken as a guide, for instance for manoeuvres involving little available turning room (Tzeng, 1998) or tug operations (Cauvier, 2008). The pivot point should fall close to the centre of gravity in the first case so that the swept area is the smallest possible during turning (Tzeng, 1998) while, if tugging a ship, the farther from the centre of gravity the pivot point is located, the more effective the lateral forces exerted by the tug are and the smaller the turn is (Cauvier, 2008). Given its usefulness for manoeuvring practical issues, this topic has mainly been addressed by publications orientated towards ships' captains or commanders. None-theless, some kinematic definitions enable this point's position to be evaluated; some dynamic theories offer an estimate of the pivot point's steady state location. These methods are useful tools for assessing the pivot point from the design stage onwards (Tzeng, 1998).
Available bibliographic sources provide a lot of information about the relationship between pivot point position and manoeuvrability characteristics regarding different operating conditions, the shape of a ship and its propulsion system. Emphasis is currently placed on making a clear difference between PP and centre of lateral resistance (COLR), taken as the point of leverage for effective lateral forces, because such difference is not clearly pointed out in some references and the concepts handled there could mislead one to the incorrect conception that the PP is the centre of leverage for yaw moments. The PP is an effect of motion and is not a property or something intrinsic regarding a ship (Cauvier, 2008); its position is a function of the lateral forces acting on a vessel and this is why its location is not a fixed point (Port Revel, 2011). By extending the latter concept, by assuring that PP position varies as a function of the pressure fields around a ship, it becomes clear that design features, such as geometry and propulsion devices, and external factors, like restricted waters, both affect a ship's speed and attitude, interaction with other bodies and the action of wind and currents may also modify PP location.
Regarding a ship's proportions, it has been stated that a bulkier vessel having a wider beam features a PP closer to the bow when moving ahead and turning (Cauvier, 2008). This is observed along with greater underwater resistance forward of the PP, being compensated for by a more open drift angle (Hooyer, 1983).
Regarding the effects of depth on manoeuvrability, it has been noticed that larger turning diameters have been identified in shallow water, involving smaller drift angles followed by greater advance, greater speed loss due to increased resistance, squat, and it has been noticed that larger rudder angles are needed to achieve the same handling characteristics as in deep water manoeuvring (Southampton Institute, 2001; Sagarra, 1998). This behaviour has been extensively reported and studied and has been observed in mathematical models of motion, being named the standard effect (Yoshimura, 1988). The same variations have been reported elsewhere (Hooft, 1973), but a specific mention having been added about the PP, which, according to the author, becomes displaced backwards when depth is shifted from deep to shallow water, therefore falling closer to the centre of gravity. An explanation has been provided by Cauvier (2008) by stressing that transversal force (lift) is larger in shallow water than in deep water, and thereby the PP comes closer to the COLR, and thus drift is less. By contrast, it is believed that there is increased pressure abaft of PP in shallow water and that the drift angle so obtained becomes smaller to avoid excessive resistance (Hooyer, 1983).
When analysing a propulsion system, it is clear that when a very effective lateral force is applied, a greater moment is generated and a wide drift angle is produced to compensate for such resistance (Cauvier, 2008). This is seen, for example, on boats having off-board or jet propulsion, allowing a tighter turn and greater drift angle than a typical propeller-rudder system (US Coast Guard, 2003).
Available information concerning the design, numerical models and experimental results related to the Colombian Navy's river support patrol vessel (RSPV) (Carreño, 2011) has been collected as the main study material. The RSPV has a bulky hull, having a high beam-draft ratio and is propelled by a pumpjet system consisting of a pair of centrifugal pumps having steerable discharge, located at the stern. A set of fullscale experiments was made with this vessel having different initial speeds, water depth levels and propulsion system jet angles (Carreño et al., 2011). A non-linear mathematical model was developed to simulate this design's manoeuvrability in three degrees of freedom (DOF), based on published formulations and test data regarding resistance to advance and self-propulsion work with a scale model (Carreño et al., 2012). Having this information available enabled assessing actual PP behaviour with the full-scale results and thus test the existing equations related to the PP position.
Dynamic concepts
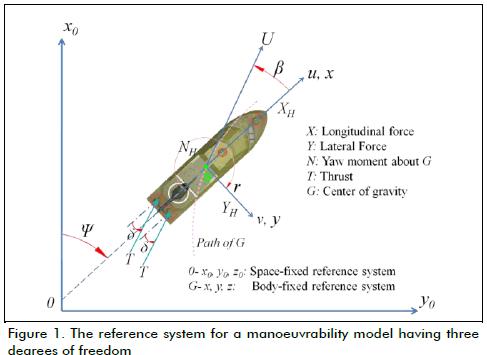
Figure 1 shows the reference system and definition of the variables involved in the 3-DOF manoeuvrability model. A key is provided showing the direction of the plotted vectors (position, speed and forces) and angles (drift β, heading ψ and jet/rudder δ) on the diagram.
The concepts presented by the Japanese Mathematical Modelling Group (MMG) (Inoue, 1981; Lee & Kijima, 2006) and other authors (Pérez & Clemente, 2007), regarding a complete model for manoeuvrability, govern a description of surface ship motion defined by the following equation system:
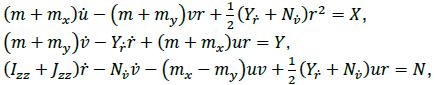
in which three DOF or system unknowns are linear speed u and v and angular yaw speed r. Variables mx, my, Jzz, ̇r and ̇v are added inertia terms arising from the motion of an object in a fluid. Variables X, Y and N are exerted forces and moment acting on a vessel, whose hydrodynamic part may comprise linear terms only or include non-linear components too.
By following the already shown convention, according to the PP definition given above, one can proceed to kinematic analysis. Local sideways speed can be denoted by ̇(x), defined as follows:
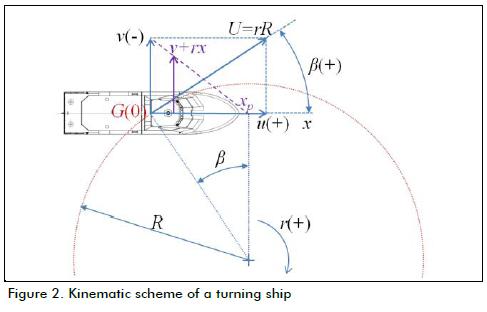
Figure 2 shows the meaning of this equation, displaying the kine-matic scheme for a turning circle manoeuvre. A PP, longitudinally located at xp, produces nil local sideways speed; then:
Therefore:
Starting from this equation, several formulae can be stated for calculating the PP by using turning ship dynamics theory:
•Formula 1: is derived directly from the physical concept (Fossen, 2011; Tzeng, 1988) :
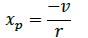
•Formula 2: is obtained from manoeuvre kinematics (Sagarra, 1998) (see Fig. 2):
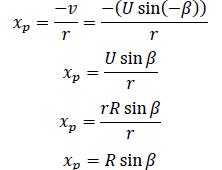
Formulae 1 and 2 are theoretically equivalent, but when real data are used they might return differing numerical results due to likely measurement errors acquired in the experiments in addition to the acceleration still present at the time of measuring which have led to a loss of equivalency between the two afore-mentioned formulae since they are deducted regarding steady motion.
•Formula 3: is deduced from linear manoeuvrability theory, assuming a steady state and applying this to the second order Nomoto model (Fossen, 2011; Tzeng, 1988):
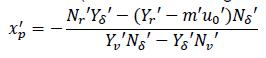
where Yv', Yr', Nv', Nr', Yδ', Nδ' are the non-dimensional forms of the hydrodynamic linear derivatives (coefficients) associated with yaw and sway. The first four may be estimated by using the vessel's geometric particulars by means of equations obtained from regression data regarding several hull types. The last two derivatives are related to the effect of propulsion and the angle applied to this handling system (δ), depending on how e way propulsion forces and moments are mathematically modelled. The lateral component of propulsion ( YP ) in this model is as-sumed to be a linear expression regarding angle δ, as follows:
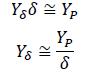
Supposing that the pumps on both starboard and port sides produce equal effects, the transversal propulsion force becomes simplified (regarding that developed by Carreño, 2011), so its associated coefficient yields:
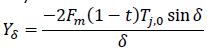
Fm is the manoeuvre factor (pump service factor for the manoeu-vre's initial speed), t is the thrust deduction and Tj,0 is the nomi-nal thrust generated by each pump, varying concerning ship speed and water depth during a set manoeuvre. Concerning yaw, derivative includes only the moment caused by transverse force , and does not take into account the moment that could appear because of the longitudinal components of propulsion which would only exist if starboard and port thrust had different magnitude.
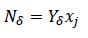
where is the longitudinal position of propulsion pump dis-charge. Based on the above definitions, these two derivatives can be eliminated from formula 3, as Yδ'can be factorised off the expressions in both numerator and denominator, thereby making the formula free of propulsion specifications. The expression thus becomes:
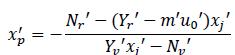
Information about the vessel being studied
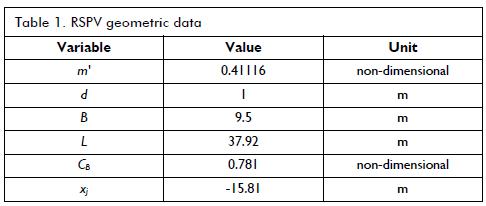
The ship in question in this paper was a river support patrol vessel (RSPV), developed by COTECMAR, serving in the Colombian navy (Fig. 3). Its hull was similar to that of a river vessel having small deadrise and high beam-draft ratio, designed to sail in very shallow water; Figure 4 gives the ship's profile. The propulsion system consisted of a pair of Schottel pumpjet centrifugal pumps (ref. SPJ 82RD), powered by two MTU (series 60) diesel engines producing 450 BHP at 1,800 rpm, coupled through reduction and reverser gear along with a cardan shaft. The pump jet can be steered through a full 360° range, individually or in tandem, by a joy-stick control on the bridge or locally from the engine control room.
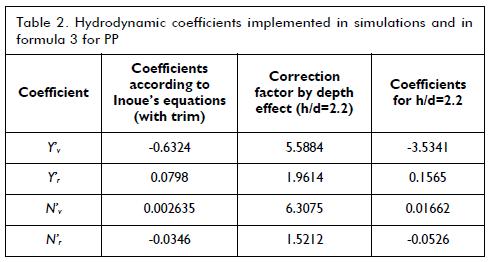
Specific information was needed re the vessel being analysed for calculating the coefficients associated with manoeuvrability and thereby some particulars of the RSPV are summarised and presented in Table 1. The non-dimensional version of all variables involved in the model follows Prime system - II (Fossen, 2011).
The linear coefficients proposed by Inoue (1981) were used when computationally running the model; their value was evaluated considering the vessel's particular data. Table 2 shows the coefficients used, whether the simulated case was in deep or shallow water. Such hydrodynamic derivatives were used for evaluating formula 3.
Results
Besides the information given above regarding the RSPV's features, enough complete data was collected from experimental tests on scale models of several types of ship regarding water depth. In addition to the above, Table 3 shows data extracted from publications concerning other vessels (Lee & Kijima, 2006; Yoshimura & Sakurai, 1988) in which motion parameters for every ship are reported for a manoeuvre at a constant rudder angle but in two different depth conditions. The output data were yaw rate r, steady state absolute speed Us, drift angle β and steady turning radius R, along with distances between G and the PP (xp shown in length units and in non-dimensional form). Regarding "ship C" (taken from Lee & Kijima, 2006) it was not possible to estimate its PP by applying formula 3 because the necessary coefficients were unknown. For all models reported here, xp was measured regarding G, except the wide-beamed vessel (Yoshimura & Sakurai, 1988) whose position was meas-ured from amidships O (G located 3.39% of L forward of O).
Discussion of the results
The present study revealed PP variation for a vessel having non-conventional propulsion and wide-beamed configuration, whose manoeuvrability in shallow water was denoted as being non-standard (NS) (Yoshimura & Sakurai, 1988). Despite the RSPV's particulars, it is worth remarking that the most usually mentioned trend was proved here by using three dynamic formulae. This pattern consisted of the PP approaching the centre of gravi- to deep water).
Research on RSPV manoeuvrability has shown the predominance of its motion's non-linear nature (Carreño, 2011), this feature explaining a significant discrepancy between the results obtained with formula 3 and those of formulae 1 and 2 as the former were derived from a linear model which might give a good approximation for some vessels (Fossen, 2011) but was not appropriate for that being analysed here.
Table 5 highlights a decrease of xp when a ship shifted from deep to shallow water, whichever formula was used or ship evaluated, thus proving the most common premise about the PP in shallow water. This was complemented by the fact that the drift angle decreased and final speed had less relative loss than in deep water, thereby agreeing with the pertinent literature. It can be appreciated that a wide-beamed ship in deep water had a PP falling further forward than in other models, showing good agreement between numerical results and published information. The shift in PP location due to variation in depth was more pronounced for a wide-beamed vessel than one having a conventional beam, even if formula 3 result was considered less accu-rate. This last feature should be considered the most important finding in this work since this pattern has not been reported previously.
Conclusions
Full-scale tests experimentally proved the effect of shallow water manoeuvring on the PP, i.e. the shallower the depth, the more the PP moves backwards approaching G. This variation was present regardless of the ship's type of propulsion or its shape.
A more pronounced effect in PP variation was observed for a wide-beamed ship using different evaluation methods.
It was shown that the Nomoto model-derived method (Formula 3) had a poor approximation level because of the non-lineal nature of the RSPV's motion.
Nomenclature
References
Carreño, J. E., Simulación de maniobras de buques con sistemas de propulsión no convencional en aguas poco profundas. Madrid, Spain: Universidad Politécnica de Madrid, PhD thesis. 2011 [ Links ]
Carreño, J. E., Jimenez, V. H., & Sierra, E. Y., Ship Manoeuvrability: Full Scale Trials Of Colombian Navy Riverine Support Patrol Vessel. Ship Science and Technology , Vol. 5, No. 9, 2011, pp. 69-86. [ Links ]
Carreño, J. E., Mora, J. D., Pérez, F. L. Mathematical model for manoeuvrability of a riverine support patrol vessel with a pumpjet propulsion system (Submitted to Ocean Engineering Journal, March 2012). [ Links ]
Cauvier, Hughes. The pivot point. The Pilot, Oct. 2008 No.295. [ Links ]
Fossen, T. I., Handbook of Marine Craft Hydrodynamics and Motion Control (First ed.). Chichester, U.K.: John Wiley & Sons, 2011. [ Links ]
Hooft, J. P. Manoeuvring Large Ships in Shallow Water-I. Journal of Navigation, Vol. 26, 1973, pp. 189-201. [ Links ]
Hooyer, Henry H. Behavior and handling of ships. Cornell Maritime Press. Centreville, Maryland.1983. [ Links ]
Inoue, S., Hirano, M., & Kijima, K., Hydrodynamic Derivatives on Ship Manoeuvring. International Shipbuilding Progress, Vol. 28, No. 321, 1981, pp. 112-125. [ Links ]
Lee, S., Kijima, K., Furukawa, Y., & Nakiri, Y., Ship Manoeuvring Characteristics as Function of Ship Form in Shallow Water. Proceedings MARSIM'06 . Terschelling, Netherlands, 2006. [ Links ]
Pérez, F. L., & Clemente, J. A., The influence of some ship parameters on manoeuvrability studied at the design stage. Ocean Engineering Vol. 34, 2007, pp. 518-525. [ Links ]
Port Revel Shiphandling. The Pivot point. October 2011. [ Links ]
Sagarra, Ricard Marí. Maniobra de los buques. Edicions UPC 1998. [ Links ]
Southampton Institute, (Warsash Maritime Centre). Notes on shiphandling. 2001 [ Links ]
Tzeng, Ching-Yaw. Analysis of the pivot point for a turning ship. Journal of Marine Science and Technology, Vol. 6, No. 1, 1998, pp. 39-44. [ Links ]
U.S. Coast Guard. Boat Crew Seamanship Manual. COMDTINST M16114.5C September 2003. [ Links ]
Yoshimura, Y., & Sakurai, H. (). Mathematical Model for the Manoeuvring Ship Motion in Shallow Water (3rd Report). Journal of KSNAJ , Vol. 211, 1988, pp. 115-126 [ Links ]