Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.34 no.2 Bogotá May/Aug. 2014
https://doi.org/10.15446/ing.investig.v34n2.42158
http://dx.doi.org/10.15446/ing.investig.v34n2.42158
G. Beltrán1 and M. Romo2
1 Gloria Beltrán. Ingeniera Civil, Magíster en Geotecnia, Universidad Nacional de Colombia, Colombia. Doctora en Ingeniería - Ingeniería Civil - Geotecnia, Universidad Nacional Autónoma de México, México. Affiliation: Departamento de Ingeniería Civil y Agrícola, Universidad Nacional de Colombia, Colombia. E-mail: gibeltranc@unal.edu.co
2 Miguel Romo. Ingeniero Civil, Universidad Autónoma de Guadalajara, México. Maestro en Mecánica de Suelos, Universidad Nacional Autónoma de México, México. PhD en mecánica de Suelos, University of California, Berkeley, USA. Affiliation: Instituto de Ingeniería, UNAM, méxico. E-mail: mromo@pumas.iingen.unam.mx
How to cite: Beltrán, G., & Romo, M. (2014). Assessing artificial neural network performance in estimating the layer properties of pavements. Ingeniería e Investigación, 34(2), 11-16.
ABSTRACT
A major concern in assessing the structural condition of existing flexible pavements is the estimation of the mechanical properties of constituent layers, which is useful for the design and decision-making process in road management systems. This parameter identification problem is truly complex due to the large number of variables involved in pavement behavior. To this end, non-conventional adaptive or approximate solutions via Artificial Neural Networks - ANNs - are considered to properly map pavement response field measurements. Previous investigations have demonstrated the exceptional ability of ANNs in layer moduli estimation from non-destructive deflection tests, but most of the reported cases were developed using synthetic deflection data or hypothetical pavement systems. This paper presents further attempts to back-calculate layer moduli via ANN modeling, using a database gathered from field tests performed on three- and four-layer pavement systems. Traditional layer structuring and pavements with a stabilized subbase were considered. A three-stage methodology is developed in this study to design and validate an "optimum" ANN-based model, i.e., the best architecture possible along with adequate learning rules. An assessment of the resulting ANN model demonstrates its forecasting capabilities and efficiency in solving a complex parameter identification problem concerning pavements.
Keywords: Artificial neural networks, pavements, non-destructive testing, deflections, layer moduli.
RESUMEN
Una de las principales preocupaciones en la evaluación de la condición estructural de pavimentos flexibles en servicio, es la estimación de propiedades mecánicas de las capas, útiles para el diseño y toma de decisiones en los sistemas de gestión de carreteras. Este problema de identificación de parámetros es realmente complejo, debido al gran número de variables involucradas en el comportamiento de los pavimentos. Para esos fines, se ha considerado modelar la respuesta del pavimentos ante pruebas de campo, mediante soluciones adaptativas o aproximadas no convencionales usando Redes Neuronales Artificiales - RNAs. Las investigaciones previas han demostrado la capacidad excepcional de las RNAs para estimar módulos de capas, a partir de pruebas no destructivas de deflexión; sin embargo, la mayoría de los casos reportados han utilizado datos sintéticos de deflexión, o sistemas de pavimento hipotéticos. En este trabajo se presentan nuevos intentos para retrocalcular los módulos de capa con modelos de RNAs, a partir de una base de datos obtenida de pruebas de deflexión realizadas en campo sobre sistemas de pavimento de tres y cuatro capas; se consideraron estructuras tradicionales y pavimentos con capas de subbase rigidizada. Para el diseño y validación del modelo "óptimo" de RNAs, es decir, la mejor arquitectura posible y el algoritmo de aprendizaje más adecuado, se desarrolló una metodología en tres etapas. La evaluación del modelo neuronal resultante, muestra su capacidad y eficiencia de predicción para resolver un problema complejo de identificación de parámetros en pavimentos.
Palabras clave: Redes neuronales artificiales, pavimentos, auscultación no destructiva, deflexiones, módulos de capa.
Received: February 19th 2014 Accepted: April 21th 2014
Introduction
The remaining service life and maintenance decisions of existing pavements are highly dependent on structural conditions during their operation. In particular, flexible pavements are considered as multilayer systems under repeated loading, whose structural response significantly depends on the features of the pavement layers: materials, stiffness, strength and thickness.
The structural condition of pavements can be properly evaluated using non-destructive surface deflection testing; impulse load devices, such as Falling Weight Deflectometers (FWDs) and Heavy
Weight Deflectometers (HWDs), are most likely the most commonly used measuring devices for this purpose. Based on the measured responses of pavements in deflection tests, it is possible to estimate material layer moduli through back analyses. To address this complex, non-linear, multivariate parameter identification problem, more efficient methods should be considered.
Many studies have used Artificial Neural Networks, ANNs, as an efficient, non-deterministic and very realistic approximation method for solving parameter identification problems, with a large potential as a complementary or alternative analysis method. ANNs have demonstrated the ability to successfully map pavement responses at a high processing speed, yielding results in real-time.
The first results of ANN modeling in the estimation of layer moduli, using FWD deflection basins, were reported in the 1990s (Meier and Rix, 1994, 1995; Tutumluer and Meier, 1996; Lee et al, 1998). Other studies have been performed for specific tasks: reducing computational time (Saltan et al, 2013; Rakesh et al, 2006), creating new deflection basins to construct a reliable ANN when the available data are scarce (Saltan and Terzi, 2008), and evaluating the effect of the ANN settings on the modeling performance (Goktepe et al, 2006; Sharma and Das, 2008).
Although good estimates have been achieved, most prior studies have been conducted using synthetic data and hypothetical pavement sections. Hence, the ability of ANN modeling was constrained by the selected range and distribution of the synthetic training data used. It should be emphasized that this is not an exclusive limitation of the ANNs as any method of analysis is sensitive to the quality of the databases.
There have been attempts to analyze field data using ANNs: a back-calculation procedure from FWD time history deflections and surface-wave measurements was proposed (Kim et al, 2000); however, the results were limited to the magnitude of the load used to generate waves. More specific analyses have been conducted on airport pavement (Gopalakrishnan and Thompson, 2004), full-depth structures (Ceylan et al, 2005) and subbase layer materials (Saltan and Sezgin, 2006).
The most recent studies have focused on developing more accurate and efficient models using optimization algorithms and hybrid systems (Kim et al, 2010; Gopalakrishnan and Khaitan, 2010; Gopalakrishnan, 2010; Nazzal and Tatari, 2013). However, few of the above mentioned studies have addressed the design process of ANNs.
In this investigation, a number of analyses were performed to define the best possible architecture along with adequate learning rules and the proper settings of the ANN model. Furthermore, a new procedure to increase the forecasting capabilities of ANNs is advanced in this paper. The database used includes wide ranges of parameter values obtained from impact deflection tests, performed on existing three- and four-layer pavement systems.
An assessment of the resulting ANN model demonstrates its forecasting capabilities and flexibility in performing analyses under particular considerations; efficiency is demonstrated by its low computational cost. Further model validation is performed by verifying the coherence between the predicted behavior and the actual observed pavement conditions.
Impact load deflection test
Impulse load tests using FWD and HWD devices properly simulate traffic loading features such as type, magnitude and time-varying vehicle loading. These devices apply an impulse load (Q) through a mass in free fall on a circular plate placed on the pavement surface, where the vertical displacement response (D1, D2,..., Di) is recorded by various sensors located at different distances from the impact point, as shown in Figure 1. Accordingly, a deflection basin can be defined; the maximum displacement, known as the peak deflection, occurs beneath the loading point.
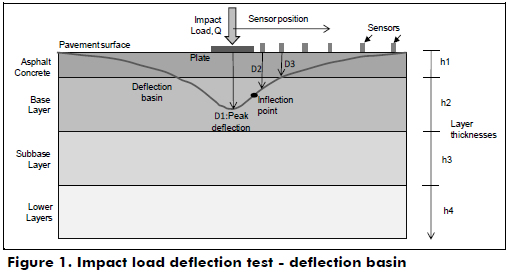
The scope and limitations of this testing procedure should be considered in a proper interpretation of the deflection data: all parameters derived represent the loading and environmental conditions at the time of testing. It should also be borne in mind that most analytical methods are not suitable when either extensive deterioration or thin layers exist in the pavement (ASTM, 2003).
Traditional estimation of layer moduli
In the technical literature, a number of procedures to back-calculate layer moduli from deflection data have been discussed (Goktepe et al, 2005; Goel and Das, 2008). Statics- and dynamics-based approaches (Chatti et al, 2004; Loizos et al, 2005; Seo et al, 2013) provide both closed-form solutions via layer-elasticity theory and numerical solutions via finite element methods. Although non-linearity in material behavior can be considered in the analyses, the cost and the computational complexity increase considerably; therefore, simplified assumptions, such as the linear and elastic behaviors of the materials, have to be assumed to efficiently solve the problem.
In common practice, the back-calculation problem is reduced to a basic principle of action (applied load) and response (deflections), both related by any known law of soil material behavior (e.g., elastic, critical state, or viscoelastic): layer moduli are first assumed to compute theoretical deflections, and the moduli are then adjusted through an iterative process, attempting to match the computed and measured deflections by minimizing an error function until certain criteria for acceptance are met.
However, the trial-and-error approach coupled with multilayer elasticity theory does not necessarily provide a unique set of modulus values, In fact, different combinations of layer moduli could lead to similar errors, and therefore, diverse solutions can be obtained (Mehta and Roque, 2003); thus, good judgment is required to select the most reasonable solution. In spite of traditional method constraints, the obtained estimations are widely accepted, given the complexity of pavement behavior modeling.
Artificial Neural Networks
ANNs are computational tools in which learning and adaptation converge to develop "intelligent" software that enables the modeling of complex and variable systems. ANNs use prior knowledge to solve a problem by incorporating new information throughout an evolving learning process to increase their forecasting capabilities. This feature enables the development of algorithms that better mimic humans' way of thinking. Accordingly, complex nonlinear problems can be treated more rationally when multivariate models for regression computations are developed or when pattern recognition from a data set is the issue at hand.
This technique is inspired by the complex structure and efficiency of the human brain, where intelligence is the result of the high connectivity between large numbers of neurons (Haykin, 1999). Similarly, ANNs are formed by interconnected processing neurons that receive, process and transmit signals or information to other connected neurons. Each link has an associated value called a weight, which can be fitted to simulate a particular feature or behavior.
An ANN is a parallel multilayer structure formed by an input layer, hidden layers and an output layer; each layer is constituted by neurons, as shown in Figure 2.
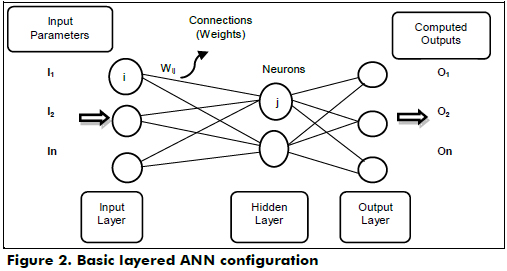
The results of ANN modeling largely depend on how the neurons are interconnected (architecture) and on the strength of these connections (weights values). Complex architectures have been commonly associated to non-linear, multi-dimensional problems. Typical elements of an ANN system are learning rules, error functions, input functions, and transfer functions, all of which have to be defined through a trial-and-error process.
There are two stages in ANN model development. The first stage is the training stage, wherein learning is achieved from input-output data sets; the learning process could be supervised if the desired outputs are given for the specified inputs or reinforced if the desired outputs are somewhat known (Logical Designs Consulting, Inc., 1996). The second stage is the testing stage, wherein the ability of the ANN to yield reasonable outputs for new data sets is evaluated; all performance statistics must be reported using the testing data. When suitable results are obtained in both stages, the resulting ANN is said to be a model capable of making reliable predictions from unknown data sets.
For solving parameter identification problems via ANNs, input variables and desired outputs are presented to the network, whereby each is associated to a neuron; the network assigns initial values to the weights, which are adjusted during successive iterations. After each iteration, the network provides outputs that are compared with desired outputs until a given error criterion is satisfied. It is then said that the network has naturally learned the input-output relations. In this study, the Mean Absolute Error, MAE, function was used as a convergence criterion
MAE=∑|( Dijmeas - Dijcomp)|) ⁄ M,
where
Dijmeas = measured deflection at sensor i for basin j
Dijcomp = computed deflection at sensor i for basin j
M = number of basins * number of sensors
It was determined that the MAE reduces the effect of atypical or dispersed values (LDC. Inc. 1996), which is an advantage for the case studied here, given the variety of pavement responses that depend on environmental conditions, deterioration, etc.
It is worth mentioning that once a well-trained ANN is developed, it can obtain fast and reliable predictions. Furthermore, by introducing plasticity (the ability to always learn) into the ANN, new information in the network's long-term memory can be assimilated. Henceforth, the ANN capabilities are enhanced.
Application
A 28 km road length with two lanes was selected as the case study. Based on available information, the parameters listed in Table 1 were selected to create the database for the pavement structural analysis. Figure 1 shows the main parameters related to deflection testing that were considered in this study. The applied loads vary between 4 and 7 tons, and seven sensors located at 0.0 m, 0.3 m, 0.45 m, 0.6 m, 0.9 m, 1.2 m and 1.8 m from the loading point were used for the deflection basin measurements.
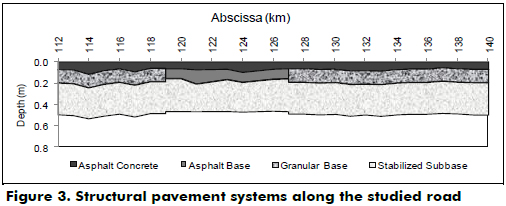
As illustrated in Figure 3 and in Table 2, there are two types of pavement systems within the 28 km road stretch: a three-layer system (from abscissa 119 to 127), where the stiffness of the layers decreases with depth, and a four-layer system (elsewhere along the road) having a subbase stiffer than the granular base.

The analysis procedure advanced in this study can be summarized in three stages. The first one is related to the ANN design and training process, which uses the available database on the road right lane. In the second stage, the forecasting capabilities are assessed using different data from that used for training the ANN system (road left lane). The final stage is an additional verification of the proposed model, performed by comparing the predicted layer moduli values with the actual condition of the pavement.
First stage: The ANN design and training process
For the purposes of designing an ANN to predict layer moduli, the first task was to identify significant variables in the input-output data sets. Given the large number of variables that affect pavement behavior, sensitivity analyses were conducted to identify the most influential variables.
Twelve variables were identified as the input set to account for most of pavement response during the loading deflection test: the load level (Q), layer thicknesses (h1, h2, h3, h4) and the surface pavement deflections in each test (D1, D2, D3, D4, D5, D6, D7). Typical values of Poisson's ratio were assumed for each layer material (0.3, 0.4, 0.35 and 0.45 for the asphalt layer, granular base, stabilized subbase and lower layer, respectively).
Regarding the output, the moduli calculated by Orozco (2005) via layered-elasticity theory (ELET) from the same deflection testing database were considered as an initial approximation for Etarget in the ANN training process. The resulting ANN configuration was the three-layer feed-forward model illustrated in Figure 4.
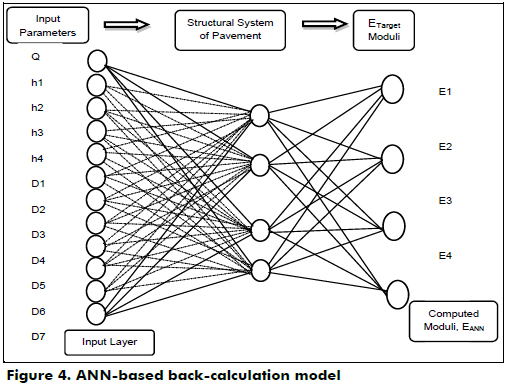
To define the ANN architecture and the learning rule that led to better results, a sensitivity study was performed, considering 18 combinations, as shown in Table 3; supervised and graded learning were used in the training stages.
In this first stage, the two processes illustrated schematically in Figure 5 were developed: the ANN design and the deflection basin verification. The sensitivity study enabled the definition of the mean standard deviation as pre-processing, dot product as the input function, and sigmoid as the transfer function.
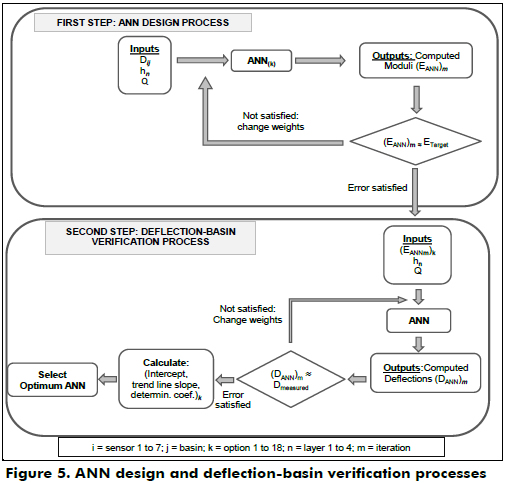
The approximation between the target moduli Etarget and the computed EANN was evaluated using the error criterion MAE; the decreasing trend in the error was checked every 500 iterations. If this trend was not observed, the new Etarget values for the following considered iterations were the last iteration EANN values (see the first step in Figure 5). This greatly enhances the possibility of meeting the adopted convergence criterion.
As has been reported by Mehta and Roque (2003), different combinations of layer moduli could lead to similar errors. To assist in selecting the more adequate set of moduli, a deflection basin verification process was conducted via ANNs.
The computed moduli EANN obtained for each option were used as inputs, and measured deflection basins were considered as target outputs (the second step in Figure 5). The option that yielded the smallest error between the predicted and field-measured deflection basins and better regression analysis indicators was selected as the optimal solution.
The forecasting reliability of the ANN options was judged on the basis of how well their computations matched the field-measured deflection basins. The matching accuracy was defined based on the similarity to a perfect match, which is achieved when a linear regression exists between the computed and measured deflections such that the slope of the trend line (b) is equal to one, intercept value (a) is equal to zero and determination coefficient (r2) is equal to one. These parameters were evaluated for the 18 options, but only the top five are included in Table 4.
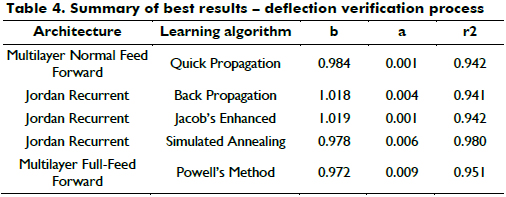
Although all five options are reliable, in this study, the Multilayer Normal Feed Forward (MLN) architecture and the Quick Propagation (QP) learning algorithm were selected because the measured and computed deflections are closer to a perfect match. Furthermore, an MAE of 2% was obtained after 485 iterations in one minute, demonstrating the computational efficiency of this ANN.
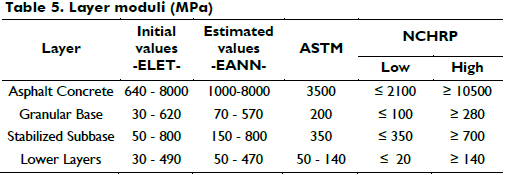
Table 5 shows the ranges of the layer moduli initially used for training the network, ELET, and those finally estimated through the optimum ANN; seed moduli suggested by the ASTM (2003) and the values reported in the NCHRP program (ARA Inc. and ERES, 2004) are also included as a reference. It is observed that most of the predicted modules are reasonable for each layer of pavement studied here. Furthermore, the ELET values vary in wider ranges than do the EANN values in all pavement layers. Low or atypical values were occasionally obtained. To identify possible causes, it was deemed important to evaluate the results along with the actual pavement's surface conditions.
It is worth noting that the above results are only conclusive regarding the network training and testing stages. However, its capability of forecasting reasonable outputs for new data that include information off the range of values used in the training and testing stages is not assured. Thus, in the next paragraph, the generalization capability of this ANN is assessed.
Second step: ANN generalization capability
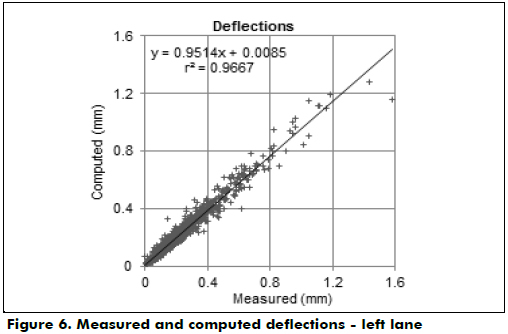
A generalization capability assessment of the optimum ANN was performed using a data set different from that used to design and train the network. The available database compiled using measurements of the left lane of the road was introduced as an input in the test set of the optimum ANN. The layer moduli were then computed for these new conditions. As observed in Figure 6, the estimated and measured deflections are in good agreement.
Third step: Final verification
Further model verification was performed by comparing the actual condition on the left lane of the road with the predicted layer moduli values. The layer material variability and the structural defects throughout the left lane were considered to this end.
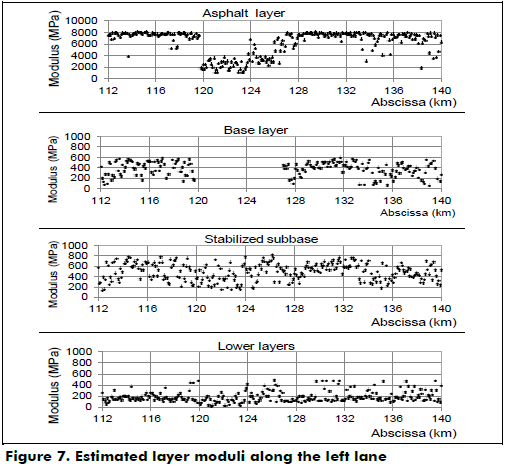
Figure 7 shows the modulus estimations for each layer along the left lane of the analyzed road. The spatial variation of the modulus shows that the asphalt concrete moduli estimated along the three-layer system (from abscissa 119 to 127) are the lowest in the road, which could be due to the lower stiffness of the asphalt base that is part of the asphalt layer (see Fig. 3). It can also be observed that the moduli estimated for the stabilized subbase layer are higher than those of the granular base along the four-layer system.
To identify the possible causes of the low or atypical values of the obtained layer moduli, the actual pavement's surface condition was included in the analysis. Figure 8 shows the peak deflections and the structural distresses of the pavement along the left lane.
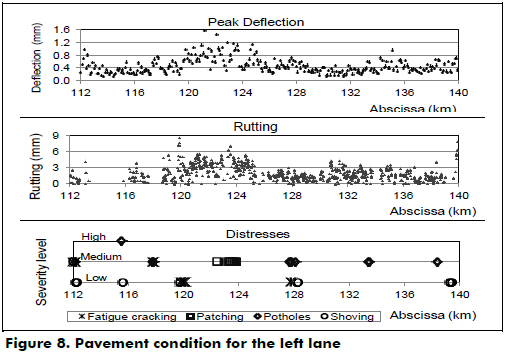
From a close inspection of Figures 7 and 8, it is reasonable to conclude that the estimated moduli values are affected by the surface condition: lower values are obtained either where deflections and rutting are higher or near to areas with more severe distresses. Accordingly, lower moduli imply deteriorated zones that deserve special attention by maintenance programs.
Conclusions
In this paper, the performance of ANN modeling in estimating the layer moduli of pavements was assessed in terms of forecasting reliability and efficiency. The developed three-step methodology enabled both the design and validation of the ANN model.
Based on the sensitivity analyses, a three-layer feed-forward ANN model with an MLN architecture and a QP learning algorithm was defined as optimum. For the case considered here, the EANN predictions fall within a narrower band than do the layer moduli estimated via multilayer elastic theory. The EANN computations were obtained in less than 1 minute using a personal computer, showing the computational efficiency of the designed ANN.
The deflection-basin verification process was most helpful for selecting the best solution among all the considered solutions. The forecasting capabilities were assessed by comparing the model predictions to the field measurements. The optimum ANN showed very good agreement: the values of the trend line slope and the coefficient of determination were close to one, and the intercept was nearly zero, with a 2% error (MAE).
The ANN generalization capability was such that the predicted layer moduli on the left lane determined via the optimum ANN very closely reproduce the pavement field-measured deflection basins.
Although most of the predicted moduli appear to be reasonable, some low values were obtained. By comparing these values with actual pavement conditions, it was determined that the pavement features are well mapped by the ANN model. Stabilized subbase-layer moduli are higher than those of the granular base. The lowest values of the asphalt layer moduli were obtained along the three-layer system, due to a combination of high levels of rutting and deflections, the presence of structural distresses, and likely, the presence of an asphalt base as a constituent of the asphalt layer.
Based on the high quality of the obtained results, it seems reasonable to conclude that the proposed ANN model can be confidently employed for the prediction of layer moduli of flexible pavements.
References
ARA Inc. & ERES Consultants Division (2004). Guide for mechanistic-empirical design of new and rehabilitated pavement structures, Final Report, Part 2. National Cooperative Highway Research Program-NCHRP, TRB, NRC. [ Links ]
ASTM D5858 (2003). Standard guide for calculating in situ equivalent elastic moduli of pavement materials using layered elastic theory (pp. 7). West Conshohocken, Pa: ASTM. [ Links ]
Ceylan, H., Guclu, A., Tutumluer, E., & Thompson, M. (2005). Backcalculation of full-depth asphalt pavement layer moduli considering nonlinear stress-dependent subgrade behavior. International Journal of Pavement Engineering, 6(3), 171-82. [ Links ]
Chatti, K., Ji, Y., & Harichandran, R. (2004). Dynamic time domain backcalculation of layer moduli, damping, and thicknesses in flexible pavements (pp. 106-116). Michigan: Transportation Research Record. [ Links ]
Goel, A., & Das, A. (2008). Non-destructive testing of asphalt pavements for structural condition evaluation: a state of the art. Journal of Non Destructive Testing and Evaluation, 23(2), 121-40. [ Links ]
Goktepe, A., Agar, E., & Lav, A. (2006). Role of learning algorithm in neural network-based backcalculation of flexible pavements. Journal of Computing in Civil Engineering, 20(5), 370-373. [ Links ]
Goktepe, A., Agar, E., & Lav, H. (2005). Advances in back-calculating the mechanical properties of flexible pavements. Advances in engineering software, 37, 421-431. [ Links ]
Gopalakrishnan, K., & Thompson, M. (2004). Backcalculation of airport flexible pavement non-linear moduli using artificial neural networks. In Proceedings of the Seventeenth International Florida Artificial Intelligence Research Society Conference (Vol. 2) (pp. 652-57). [ Links ]
Gopalakrishnan, K., & Khaitan, K. (2010). Finite element based adaptative neuro-fuzzy inference technique for parameter identification of multi-layered transportation structures. Transport, 25(1), 58-65. [ Links ]
Gopalakrishnan, K. (2010). Neural network-swarm intelligence hybrid nonlinear optimization algorithm for pavement moduli back-calculation. Journal of Transportation Engineering - ASCE, 136(6), 528-536. [ Links ]
Haykin, S. (1999). Neural Networks, a comprehensive foundation (2nd ed.). India: Prentice education Inc. [ Links ]
Kim, Y., Xu, B., & Kim, Y. (2000). A new backcalculation procedure based on dispersion analysis of FWD time history deflections and surface wave measurements using ANNs (pp. 297-312). In NDT of pavements and backcalculation of moduli (Vol. 3). ASTM Publications. [ Links ]
Kim, D., Kim, J., & Mun, S. (2010). Normalisation methods on neural networks for predicting pavement layer moduli. Road & Transport Research, 19(3), 38-46. [ Links ]
Lee, Y., Kim, Y., & Ranjithan, S. (1998). Dynamic analysis-based approach to determine flexible pavement layer moduli using deflection basin parameters. Transportation Research Record, (1639), 36-42. [ Links ]
LDC - Logical Designs Consulting, Inc. (1996). ThinksPro™ Neural Networks for Windows, User's Guide. [ Links ]
Loizos, A., & Boukovalas, G. (2005). Pavement soil caracterization using a dynamic stiffness model. International Journal of Pavement Engineering, 6, 5-15. [ Links ]
Mehta, Y., & Roque, R. (2003). Evaluation of FWD data for determination of layer moduli of pavements. Journal of Materials in Civil Engineering (ASCE), 25-31. [ Links ]
Meier, R., & Rix, G. (1994). Backcalculation of flexible pavement moduli using artificial neural networks. Transportation Research Record, (1448), 72-81. [ Links ]
Meier, R., & Rix, G. (1995). Backcalculation of flexible pavement moduli from dynamic deflection basins using artificial neural networks. Transportation Research Record, (1473), 72-81. [ Links ]
Nazzal, M., & Tatari, O. (2013). Evaluating the use of neural networks and genetic algorithms for prediction of subgrade resilient modulus. International Journal of Pavement Engineering, 14(4), 364-373. [ Links ]
Orozco, R. V. (2005). Evaluación de pavimentos flexibles con métodos no destructivos. (PhD thesis). Universidad Nacional Autónoma de México. [ Links ]
Rakesh, N., Jain, A., Reddy, M., & Reddy, K. (2006). Artificial neural networks - genetic algorithm based model for back-calculation of pavement layer moduli. International Journal of Pavement Engineering, 7(3), 221-230. [ Links ]
Saltan, M., Uz, V., & Aktas, B. (2013). Artificial neural networks-based backcalculation of the structural properties of a typical flexible pavement. Neural Computing & Applications, 23(6), 1703-1710. [ Links ]
Saltan, M. & Terzi, S. (2008). Modeling deflection basin using neural networks with cross-validation technique in backcalculating flexible pavement layer moduli. Advances in Engineering Software, 39(7), 588-592. [ Links ]
Saltan, M., & Sezgin, H. (2006). Hybrid neural network and finite element modeling of sub-base layer material properties in flexible pavements. Materials & design, 28, 1725-1730. [ Links ]
Seo, J., Kim, Y., Cho, J., & Jeong, S. (2013). Estimation of in situ dynamic modulus by using MEPDG dynamic modulus and FWD data at different temperatures. International Journal of Pavement Engineering, 14(4), 343-353. [ Links ]
Sharma, S., & Das, A. (2008). Back-calculation of pavement layer moduli from falling weight deflectometer data, using an artificial neural network. Canadian Journal of Civil Engineering, 35, 57-66. [ Links ]
Tutumluer, E. & Meier, R. (1996). Attempt at resilient modulus modeling using artificial neural networks. Transportation Research Record, 1560, 1-6. [ Links ]













