Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.34 no.2 Bogotá May/Aug. 2014
https://doi.org/10.15446/ing.investig.v34n2.40141
http://dx.doi.org/10.15446/ing.investig.v34n2.40141
J. M. D. Becerra1 and J. E. Ortiz2
1 Juan Miguel David Becerra Tobar. Electronic engineer, Universidad Nacional de Colombia, Colombia. Master engineering-telecommunications, Universidad Nacional de Colombia, Colombia. Affiliation: PhD student, Universidad Nacional de Colombia, Colombia. E-mail: jmbecerrat@unal.edu.co
2 Jorge Eduardo Ortiz Triviño. System engineer, Universidad Nacional de Colombia, Colombia. Master science-statistics, Master engineering-telecommunications, Master philosophy, PhD system engineering and computation, Universidad Nacional de Colombia, Colombia. Affiliation: Associate professor, Universidad Nacional de Colombia, Colombia. E-mail: jeortizt@unal.edu.co
How to cite: Becerra, J. M. D., & Ortiz, J. E. (2014). Statistical independence of reflection and transmission coefficients on PLT due to system loads. Ingeniería e Investigación, 34(2), 71-75.
ABSTRACT
This paper presents the theoretical development of the covariance between reflection and transmission coefficients caused by system loads in electric grids. This result allows the calculation of the expected value and covariance of the channel response; these parameters can be used as design criteria in telecommunication networks over power lines in in-home environments. Additionally, the product of these variables is encountered commonly in the channel transfer function, whereby it can be determined if the calculation of these parameters can be simplified when this product is on a given path. For this purpose, the random behavior of the channel response caused by human activity is represented by a multipath model with a stochastic addition, where the reflection coefficient is treated as a random complex variable, providing more information compared to the real field.
Keywords: PLT, PLC, BPL, system load, stochastic model, covariance, channel.
RESUMEN
En este artículo se muestra el desarrollo teórico de la covarianza entre los coeficientes de reflexión y transmisión causados por cargas del sistema presentes en la red eléctrica. Este resultado permite calcular el valor esperado y la covarianza de la respuesta del canal, los cuales pueden ser utilizados como criterios de diseño en redes de telecomunicaciones sobre líneas de potencia en ambientes in-home, y el producto de estas variables es encontrado frecuentemente en la función de transferencia del canal, lo que permite determinar si el cálculo de estos parámetros puede ser simplificado para una trayectoria dada. Para tal fin, el comportamiento aleatorio de la respuesta del canal causado por la actividad humana se representó por medio de un modelo multitrayecto con una adición estocástica, donde cada coeficiente de reflexión es tratado como una variable aleatoria compleja, proveyendo más información en comparación con un espacio real.
Palabras clave: PLT, PLC, BPL, cargas del sistema, modelo estocástico, covarianza, canal.
Received: October 6th 2013 Accepted: February 25th 2014
Introduction
Power line telecommunications, also known as broadband power line or power line communications (PLT, BPL and PLC), is defined as the use of the electric infrastructure to provide telecommunication services. PLT benefits users and service providers because there is no need to build a new infrastructure or make modifications to buildings, which reduces cost and thus is of great interest to many in the telecommunication sector, including regulatory bodies. Nonetheless, the characteristics of electric wires are not the best for transmitting telecommunications signals because this network was originally intended to carry electrical power and thus is hostile to high frequency signals.
As an emergent and important technology, PLT needs a model that represents its main characteristics for implementation; how-ever, most models are deterministic, which causes difficulties when the models need to be used in other scenarios with different conditions. The Institute of Electrical and Electronics Engineers (IEEE) has taken this necessity into account and has adopted a multipath model proposed by Zimmermann and Dostert, which can accommodate these requirements (Tanabe 1012). Nonetheless, certain characteristics, such as load effects over channel response, are out of the model's scope. In fact, ignoring these effects can cause a decrease in performance of 60% in broadband communications (Avril G 2008).
Consequently, an addition of loads effects to the multipath model was made by following a bottom-up approach, which can be used in a deterministic form. Here, a load should be understood as any device connected to the power lines. This addition allows the modeling of the linear periodically time varying (LPTV) behavior of the channel (Cañete Corripio, et al. 2006), with the Zimmermann and Dostert's model.
However, the channel response will change to the other state (LPTV transfer function) if a load is turned off or on, and these changes last for a longer duration than the mains period (hours, for example). These changes are considered long-term variations or transitions between stationary states (F. A. Cañete 2002.
The long-term changes of the loads are introduced in a probabilistic way into the channel response. The response is declared as a function of a random variables set where each variable is related to one load by means of its reflection coefficient (David Becerra 2012. Because the addition of both effects is stochastic by nature, from now on, it will be referred as a stochastic edition.
Channel adaptation algorithms in PLT networks could be more easily assessed by using the expected value of the channel response, which is a function of time and frequency. The expected value offers a way to check if repeaters are needed or if one plug is not good enough to provide telecommunication services.
However, computing the expected value following its mathematical definition can be quite difficult, especially in networks with many nodes and loads. Hence, there is a need for different ways to simplify the expected value's algorithm.
Because the product of the transmission and the reflection coefficients of any load can appear in the channel response, the independence between these coefficients was studied to simplify the expected value computation. This study is presented as follows: first, a review of the multipath model is presented. Then, stochastic addition is explained based on the characteristics of the set of random variables. The next section shows a theoretical demonstration of the stochastic independence of the coefficients. Finally, conclusions are presented.
Multipath model review
Conceptually, representing the multipath behavior of electric grids is the main purpose of the model proposed by Zimmermann and Dostert. Additionally, this model includes impedance mismatching, frequency selective fading and increasing signal attenuation of typical power cables due to length and frequency in a parametric form.
This model uses the sum of every possible path transfer function that a signal can find between the transmitter and the receiver. These functions are obtained by applying transmission line theory to the PLT network. The distributed parameters that are depicted in Figure 1 are expressed as a multiplication of three factors that represent the effects mentioned above in a parametric form, as shown in equation(1).
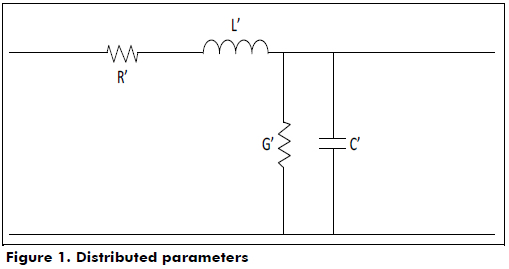
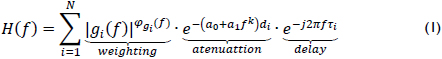
The weighting factor gives a measure of how much the i-th path is contributing to the total result and is calculated by multiplying all reflection and transfer coefficients found on the path. The attenuation term expresses the dependence of the gain on fre-quency and distance. The delay factor defines the lag of the signal when it takes path i.
Calculation of Factors: the attenuation term is computed using the propagation constant when the transmission line is matched, which is defined in (2). Hence, the transfer function can be ex-pressed in terms of the length of the path (3).
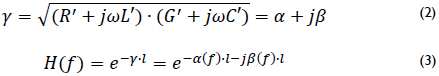
Due to the frequency range where PLT works, γ can be simplified because R' << ωL' and G' << ωC'. The result is shown in (4), where ZL is the characteristic impedance of the transmission line, defined in (5).
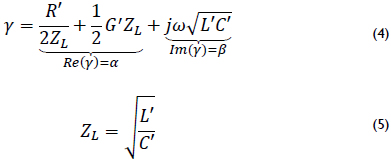
The resistance of the conductors may be proportional to the square root of the frequency or to the frequency itself. Losses due to dielectric presence are directly proportional to frequency (f), which is demonstrated using equations (6) and (7) to obtain R and G on two parallel conductors of radius r.
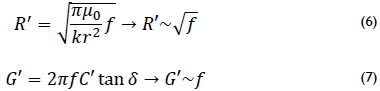
To simplify, attenuation is bounded to the alpha term of gamma (4) and can be expressed as a function of three constants a0, a1 and k; see equations (8) and (9). These parameters can be found using measurements or theoretical calculations.
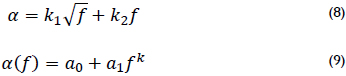
The weighting and delay are obtained from the topology of the electric grid. In figure 2, a network composed of a line with one branch is shown. This network will be used as an example of how these parameters are calculated.
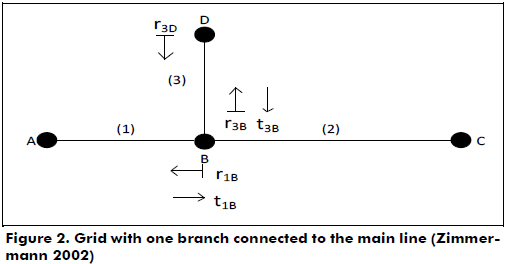
The first step is to identify the possible paths that a signal can take; the direct path is ABC. However, segments of lines are not matched, which causes reflections. Hence, other options are ABDBC, ABABC, and even ABDBDBC. Every possible path should be considered, but this is not practical. A criterion must be applied in order to obtain an efficient representation of a PLT channel. For example, channels whose weighting factor is above 10% of the direct path weighting factor have to be taken into account.
After the trajectories are defined, a product between the reflection and transfer factors of each segment of the path is needed to obtain the weighting factor. Assuming that A and C are matched (there is no reflection, hence the transmission value is one), weighting for ABC would be t1b. The weighting for ABDBC would be t1b · r3d · t3b. A similar process is performed to obtain the total length for delay and attenuation.
The delay factor depends on the path's length and is calculated using equation (10); this magnitude is related with the dielectric constant of the material and the speed of light.

Stochastic addition
To obtain a good addition of the loads effects, it is necessary to explain the existence of two main types of effects: long-term variation, which is related to human activities when turning on or off a device, which is random for PLT transmitters, and short-term variation, which depends on the load behavior.
There are four kinds of loads (that affect the reflection coeffi-cient behavior): loads that are constant in time and frequency, time-invariant but frequency-selective impedances (like RLC circuits), switching loads (diode rectifiers), and time-varying and frequency selective loads, which commonly behave in harmonic form, such as devices that use rectifiers with diodes or con-trolled silicon elements (SCRs or MOSFETs) (Jian Sun, & Karimi 2008) (Rönnberg, 2011).
Due to Zimmerman's model composition, it is clear that loads affect the weighting factor because of reflection and transmission coefficients, which are defined in equations (11) and (12) (Tanabe, 2012).

Hence, the weighting factor can be defined as a function dependent on a set of j random variables, and each variable is a reflection coefficient due to a load.
In Figure 3, a common topology found in in-home environments is shown, where ZG and ZL are impedances of PLT devices and Z1, Z2 and Z3 are in-home loads. The direct path is the trajectory 1-2-3-4-5.
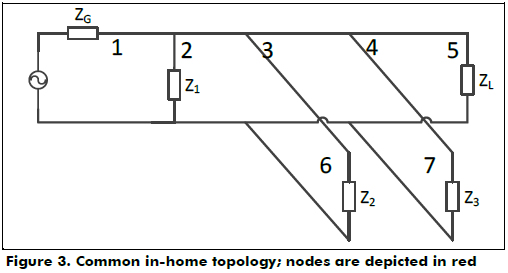
It is important to notice that Z1 is directly connected to the direct path, but Z2 and Z3 are connected through others lines because there are loads, such as phone chargers, where the cable length between the power socket and the load is not long enough to be considered as a transmission line. For instance, if the highest frequency of interest is 100 MHz, the minimum length is 30 cm.
There are two kinds of reflection coefficients: those due to loads and those that are constant, which are caused by connections between cables.
Two assumptions were made in order to add stochastic effects properly:
First, loads like Z1 are connected alone to a power socket, which allows the reflection coefficient to be defined as a function of only one load. For the other loads, this condition is unnecessary because these loads are connected to only one node and do not cause transmission coefficients due to their position. Thus, each load can only cause a reflection coefficient. A topology that fulfills this condition is shown in Figure 3.
Second, all random variables are independent or uncorrelated, which means that a state (on or off) of a load does not depend on the states of the other loads plugged to the electric grid. This condition is known to be not entirely true, for example, entertainment devices are used in conjunction with a television set, but it is an initial approach.
Each random variable is modeled with a Markov process using two states (ON and OFF) because most people do not unplug their devices (Cañete 2002). On and off states can thus be defined as shown in Figure 4: 0 when the device is off and 1 when the device is on. The duration of states are exponentially distributed (λoff and μon). Hence, a reflection would be defined as a function of frequency, state (n) and time (depending on the type of load), as shown in equation (13).
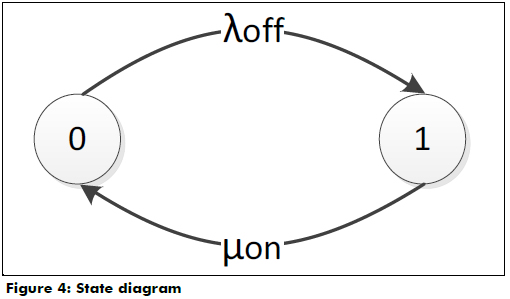
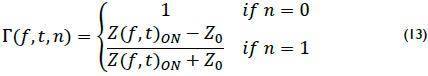
This is a truncated Poisson distribution with N = 1. The reflection factor has two possible values and an associated probability, which is shown in equation (14). The average times of use in order must be obtained to determine the probabilities for each state.
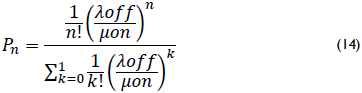
Stochastic Independence of coefficients
First, the nature of the random variables set must be understood. Because each variable is one reflection coefficient caused by a complex impedance, this variable is a complex number. Hence, this random variable set is complex, and its treatment is different than real random variables (Wooding 1956) (Fuhrmann 1999).
Second, statistical independence between two variables X and Y implies that the covariance between them is zero, but the converse is not true. However, if covariance is not zero, there is no independence.
For complex random variables, the covariance between two variables is defined as shown in (15) for the discrete case and several of its properties are shown in equations (16) and (17) (Richmond 2000) (Triviño 2012).
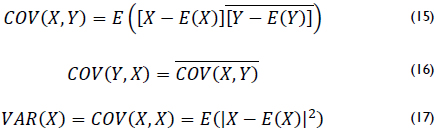
To demonstrate the independence between reflection and transmission, the coefficients represented by and t were replaced in equation (15).
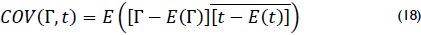
The transmission coefficient definition (12) is replaced in (18) to obtain (19).
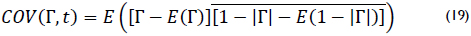
The variable t is a real numbers by definition, and conjugate of a real number is itself, obtaining (20).
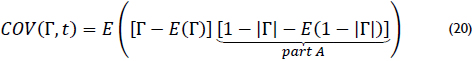
The simplification of part A of equation (20) was performed using linear properties of the expected value. The result is shown in (21).
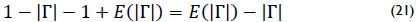
By replacing (21) in (20) and finding the product, equation (22) was found, where the expected value is applied to obtain (23).
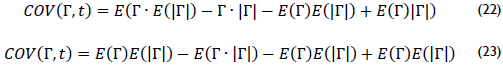
When (23) is simplified, the expected value of a function is applied to obtain (24). Hence, if the transmission and reflection coefficients are independent, then the covariance is zero. To prove this hypothesis, zero is replaced and its result is shown in (25). If that equality is not demonstrated, then there is no independence.
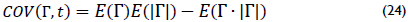
Because is a function, the expected value was calculated using the probability density function given by equation (14) and values from (13); then, (26) and (27) were obtained.
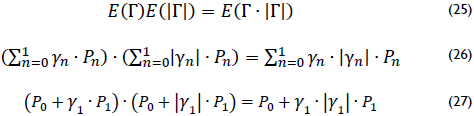
It can be demonstrated that (27) can be solved for and . However, this implies that we have a perfect short circuit connected to the network (this is very unlikely) or that the load is always an open circuit, which is nonsense.
Then, by performing the operations depicted in (27), the hypothesis that the covariance is equal to zero is shown to be false (28) for general conditions (nontrivial solutions), which means that the complex loads are asymmetric probabilities. Thus, the transmission and reflection coefficients are not independent.
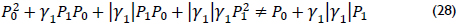
Conclusions
This work proves that the expected value of the product between transmission and reflection coefficients, caused by the same load, cannot be simplified as the product of their expected values, which is important for loads connected as Z1 shown in Figure 3. Thus, simplifying the expected value of the weighting factor is not possible when the condition given above is fulfilled.
Transmission coefficients do not affect the weighting factor for loads with cable lengths bigger than one tenth of the highest frequency wavelength.
The transmission coefficient definition allows this variable to be treated as a real number, which strongly simplifies the determination of the stochastic independence of the coefficients.
Dependence between the transmission and reflection coefficients does not depends on short-time variation, which means that there is no value in time and frequency that generates a covariance equal to zero.
Further work can be performed to prove statistical independence between powers of different exponents due to different loads, which can improve the performance of the expected value of the channel response.
References
Avril, G. (2008, October 10). Etude et optimisation des systèmes à courant porteurs domestiques fac aux perturbations du réseau électrique. INSA de Rennes. Retrieved from http://tel.archives-ouvertes.fr/tel-00334464 [ Links ]
Becerra, D., Ortiz, J., & Ramos, Z. (2013). Stochastic Behavior of Electric Grid Channel for Power Lines Telecommunications Due to Loads on In-Home Environments. Electrical and Electronic Engineering, 2(6), 379-382. doi:10.5923/j.eee.20120206.06 [ Links ]
Canete, F. J., Díez, L., Cortes, J. A., & Entrambasaguas, J. T. (2002). Broadband modelling of indoor power-line channels. IEEE Transactions on Consumer Electronics, 48(1), 175-183. doi:10.1109/TCE.2002.1010108 [ Links ]
Corripio, F. J. C., Arrabal, J. A. C., del Rio, L. D., & Munoz, J. T. E. (2006). Analysis of the cyclic short-term variation of indoor power line channels. IEEE Journal on Selected Areas in Communications, 24(7), 1327-1338. doi:10.1109/JSAC.2006.874402 [ Links ]
Fuhrmann, D. R. (1997). Complex Random Variables and Stochastic Processes. In V. Madisetti (Ed.), The Digital Signal Processing Handbook (pp. 60-1, 61-1). CRC Press. [ Links ]
Ortiz Triviño, J. E. (2012). Introducción a la teoría de teletráfico. Universidad Nacional de Colombia. Retrieved from http://disi.unal.edu.co/profesores/jeortizt/EstadTel/Archivos/14.%20IntroduccionALaTeoriaDeTeletrafico_24DeAbrilDe2012_ElPrincipal%20.pdf [ Links ]
Richmond, C. D. (2000). Multidimensional Random Variables. Retrieved from http://acoustics.mit.edu/faculty/abb/2.163/www/Random%20vectors.pdf [ Links ]
Rönnberg, S. (2011, April). Power line communication and customer equipment (Licentiate thesis). Luleå tekniska, Luleå. Retrieved from http://pure.ltu.se/portal/en/publications/power-line-communication-and-customer-equipment(8f4b1b17-adbc-4e6f-8e59-38c2bc215789).html [ Links ]
Sun, J., & Karimi, K. J. (2008). Small-signal input impedance modeling of line-frequency rectifiers. IEEE Transactions on Aerospace and Electronic Systems, 44(4), 1489-1497. doi:10.1109/TAES.2008. 4667724 [ Links ]
Tanabe, S., Viner, A., Stuebing, G., Afkhamie, K., Logvinov, O., Kamali, J., & Arroyo, S. (2010, September). Electrical Network and Topology Channel and Noise Model. Copyright ©2010 IEEE-SA. Retrieved from http://grouper.ieee.org/groups/1901/Chan nelAndNoiseModel/ChannelAndNoiseModel.pdf [ Links ]
Wooding, R. A. (1956). The Multivariate Distribution of Complex Normal Variables. Biometrika, 43(1/2), 212-215. doi:10.2307/ 2333597 [ Links ]
Zimmermann, M., & Dostert, K. (2002). A multipath model for the powerline channel. IEEE Transactions on Communications, 50(4), 553-559. doi:10.1109/26.996069 [ Links ]













