Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Ingeniería e Investigación
versão impressa ISSN 0120-5609
Ing. Investig. vol.34 no.3 Bogotá sep./dez. 2014
https://doi.org/10.15446/ing.investig.v34n3.42950
DOI: http://dx.doi.org/10.15446/ing.investig.v34n3.42950
J. A. Rodríguez-Gutiérrez1 and J. D. Aristizabal-Ochoa2
1 Jose A. Rodríguez-Gutiérrez. Ingeniero Civil, Universidad Nacional de Colombia, Medellín, Colombia. Affilliation: Universidad Nacional de Colombia, Medellín, Colombia. E-mail: alfredo1704@gmail.com
2 J. Darío Aristizabal-Ochoa. Ingeniero Civil, Universidad Nacional de Colombia, Medellín, Colombia. M. Sc. and Ph. D. University of Illinois, Urbana-Champaign, USA. Affilliation: Profesor Titular, Universidad Nacional de Colombia, Medellín, Colombia.
E-mail: jdaristi@unal.edu.co
How to cite: Rodríguez-Gutiérrez, J. A., & Aristizabal-Ochoa, J. D. (2014). Biaxial bending of slender HSC columns and tubes filled with concrete under short- and long-term loads: II) Verification. Ingeniería e Investigación, 34(3), 19-25.
ABSTRACT
An analytical method that calculates both the short- and long-term response of slender columns made of high-strength concrete (HSC) and of tubes filled with concrete with generalized end conditions that are subjected to transverse loads along the span and to axial loads at the ends (causing single- or double-curvature under uniaxial or biaxial bending) is presented in a companion paper. The columns that can be analyzed with this method include those with solid and hollow (rectangular, circular, oval, C-, T-, L-, or any arbitrary shape) cross sections and columns made of circular and rectangular steel tubes filled with HSC. In this paper, the validity of the proposed method is tested against experimental results from the technical literature that examined over seventy column specimens.
Keywords: Axial load, Biaxial bending, Columns, Composite materials, High-strength concrete, Deflections.
RESUMEN
En un artículo adjunto se presenta el método analítico para calcular las respuestas, a corto y largo plazo, de las columnas esbeltas de concreto en alta resistencia (HSC) y de los tubos rellenos de hormigón; con condiciones de apoyo generalizados, sometidos a cargas transversales de luz y a cargas axiales excéntricas en los extremos (causando curvatura simple o doble bajo flexión uniaxial o biaxial).
Los tipos de columnas que pueden ser analizadas son: ovaladas, rectangulares, circulares, C, T, L o de cualquier sección transversal arbitraria, sólida o hueca, además, las que están hechas de tubos de acero circulares y rectangulares llenos de concreto en alta resistencia. En esta publicación se presenta la validez del método y los resultados obtenidos son comparados con otros, que han sido reportados por diferentes investigadores en la literatura técnica, con más de setenta muestras de columnas.
Palabras clave: arriostramiento, pandeo, columnas, fundación elástica, pilas, conexiones semirrígidas y estabilidad.
Received: April 4th 2014 Accepted: April 25th 2014
Introduction
An analytical method that calculates both the short- and long-term response of slender columns made of high-strength concrete (HSC) and of tubes filled with concrete with generalized end conditions that are subjected to transverse loads along the span and to axial loads at the ends (causing single- or double-curvature under uniaxial or biaxial bending) is presented in a companion paper published by the authors in 2014.
The main objective of this paper is to verify the iterative analytical procedure and corresponding equations that were presented in the companion paper. The proposed model, which is capable of predicting not only the complete load-rotation and load-deflection curves (both the ascending and descending parts) but also the maximum load capacity of slender concrete columns, is verified against test results of over seventy specimens of columns reported by several researchers in the technical literature. The columns analyzed include solid and hollow (rectangular, circular, oval, C-, T-, L-, or any arbitrary shape) cross sections and columns made of circular or rectangular steel tubes filled with HSC.
Verification of Proposed Model
It is assumed that: 1) fc" = fc' for all test specimens. This is particularly valid for tubular columns subjected to axial load with large eccentricities in which the effects of the confinement of the concrete provided by the steel tube are relatively low; and 2) for circular tubular columns, the concrete core is approximated by a polygon with 16 sides, and the cross-sectional area of the tube is estimated as a total of 20 rebars uniformly distributed around the perimeter of the circle.
Columns after Cederwall et al. 1990-. A series of 22 columns made of 4.72 in. (120-mm) square, steel tubes filled with concrete and with a height of 118.11 in. (3 m) were tested under short-term loads. Column specimens made of concrete with a strength greater than or equal to 11,603 psi (80 MPa) were selected from this series to study their behavior using the proposed method. These eight specimens were subjected to end loads applied simultaneously to the steel tube and to the concrete core causing a single-curvature up to failure. Table 1 lists the thicknesses of the steel tubes, the applied end eccentricities, the yield strength of the steel tube, the compressive strength of the concrete, and the maximum experimental and theoretical axial load.
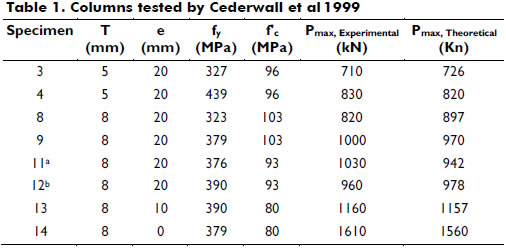
Excellent agreement between the calculated and the experimental maximum values of the axial load are shown when comparing the last two columns of Table 1. Figure 1 also shows excellent agreement between the calculated and the experimental curves (loading and unloading load-deflection responses). It is important to note that the effects of the confinement of the concrete provided by the square steel tubes in the experimental results of all specimens subjected to an axial load with low eccentricity are rather insignificant.
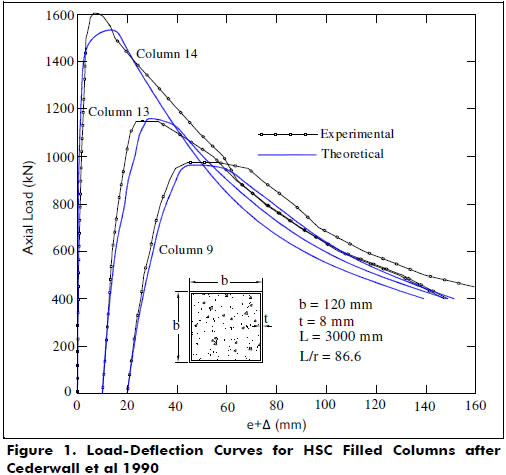
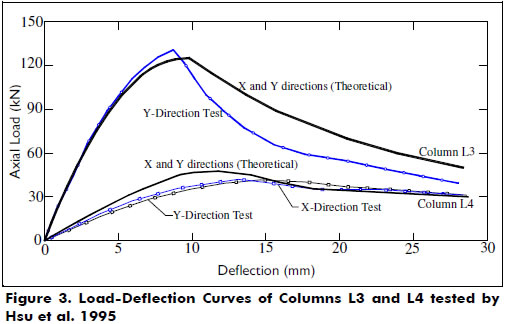
Columns tested by Hsu et al 1995-. A series of 9 columns identified as L-columns made of high-strength concrete were tested under a short-term axial load and biaxial bending. The effects of concrete strength, axial load eccentricity, steel ratio and ratio eccentricities (Θ = Tan-1(ey/ex)) were studied. All column specimens had a span length of 48 in. (1.22 m). Table 2 presents the properties of all L-columns and their corresponding experimental and calculated axial load at failure.
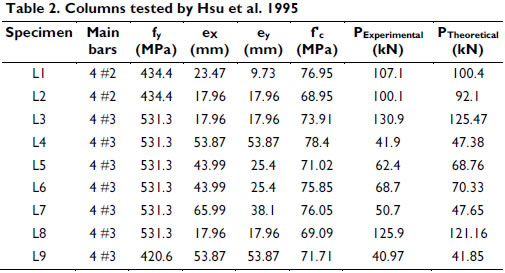
The proposed model predicts with good accuracy both the axial load and the maximum lateral deflection at failure, as well as the load-deflection response as shown by Figures 2 and 3. Figure 3 shows good agreement between the calculated and experimental curves (for both loading and unloading) for the load-deflection responses of specimens L3 and L4.
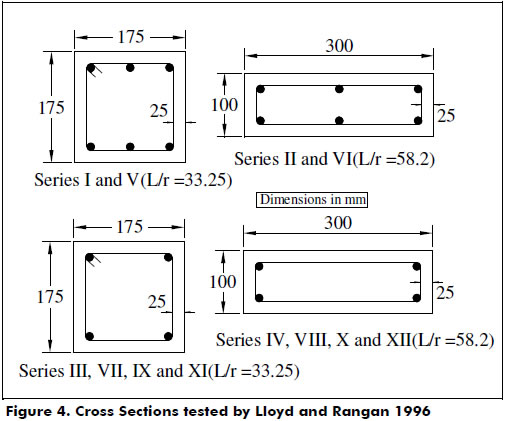
Columns tested by Lloyd and Rangan 1996-. A series of 36 columns with an effective height of 66.14 in. (1.68 m) were subjected to short-term axial load up to failure at the University of Curtin, Australia. The columns were simply supported and subjected to an eccentric axial load P causing equal moments (Pe) at both ends. The properties of the materials are as follows:
Concrete: Series I-IV: 8,410 psi (58 MPa); Series V-VIII: 13,340 psi (92 MPa); Series IX-XIII: 14,065 psi (97 MPa).
Reinforcements: The longitudinal reinforcement consisted of 12-mm steel rebars with a yield strength fy = 62 ksi (430 MPa). The transverse reinforcementconsisted of closed steel stirrups that were 4 mm in diameter with a yield strength fy = 65 ksi (450 MPa).
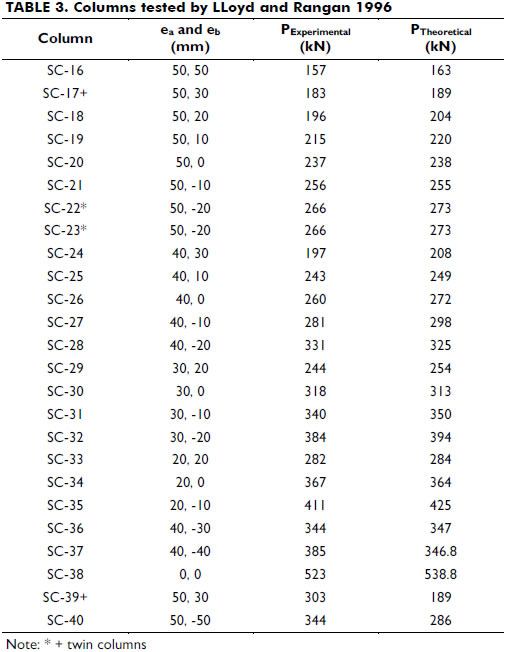
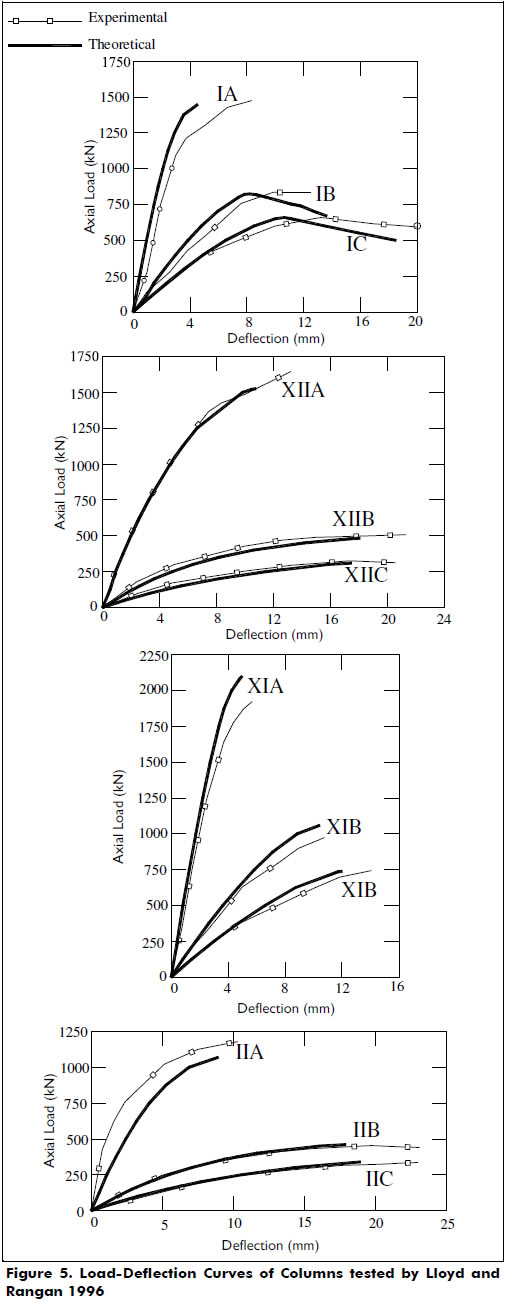
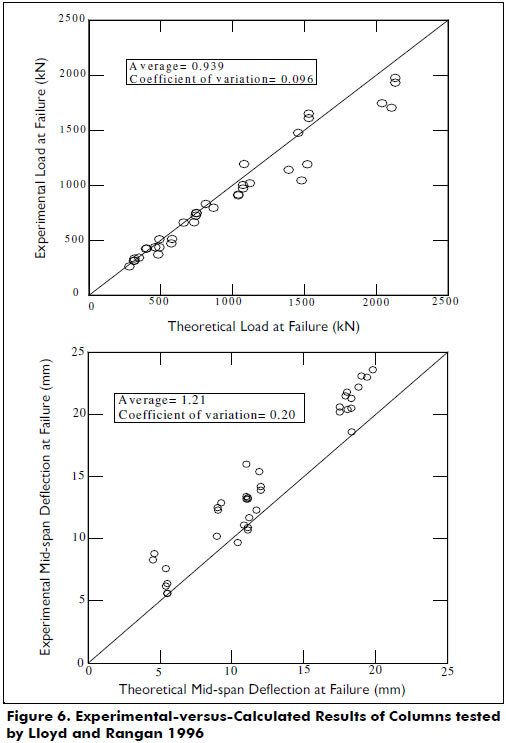
Details of the cross-sectional properties of the columns are shown in Figure 4. End eccentricities, experimental and theoretical axial load and mid-span deflection at failure are all listed in Table 3. Figure 5 shows the full load-deflection responses. Figure 6 shows the correlations of the ratios between the experimental and the theoretical values for both the axial load and the mid-span deflection. Good agreements between the calculated and experimental results were obtained.
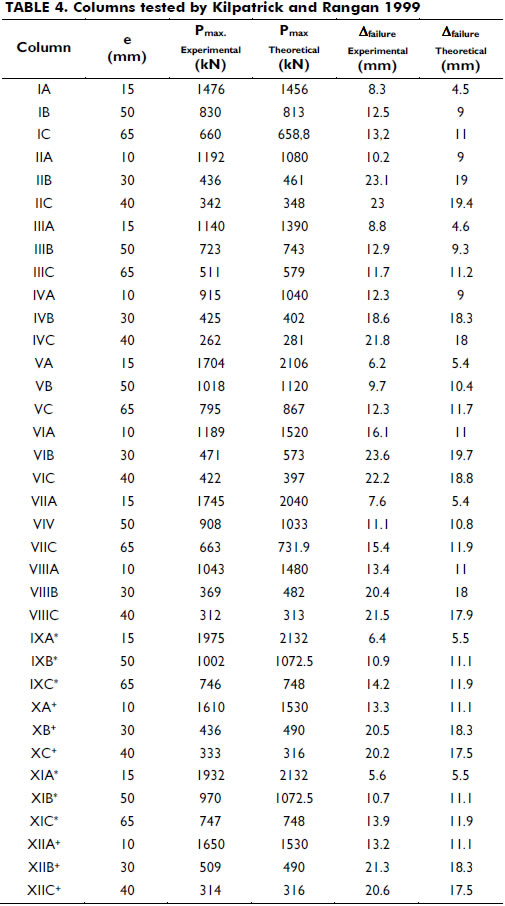
Columns tested by Kilpatrick and Rangan 1999-. Forty-one circular tubular steel columns filled with concrete were tested under short-term loads. Eleven test specimens were subjected to double curvature, the rest (thirty specimens) to single-curvature. The test specimens were made of 0.094 in. (2.4 mm) thick steel tubes of 4.05 in. (0.1015 m) in diameter and 85.63 in. (2.175 m) in length. The average concrete strength was fc'= 13,923 psi (96 MPa). The properties of the steel tube were: yield stress fy = 59.465 ksi (410 MPa), ultimate strength fu = 68.893 ksi (475 MPa), and modulus of elasticity Es = 29,733 ksi (205,000 MPa).
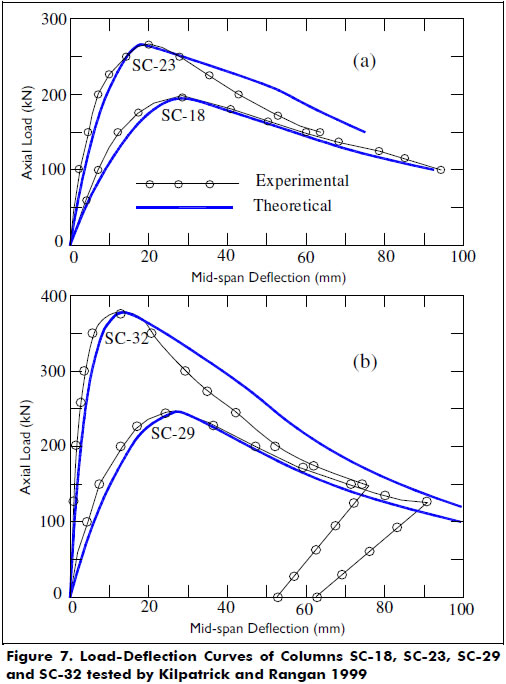
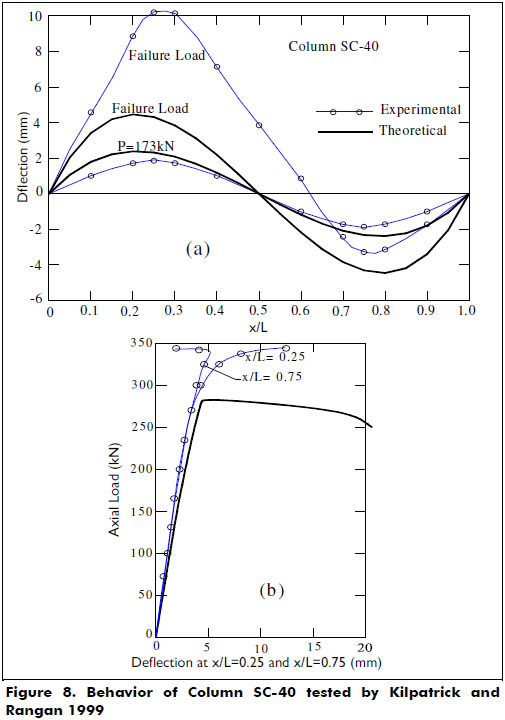
In the theoretical analyses, the concrete core was approximated by a regular polygon with 16 sides, and the steel tube was assumed to be equivalent to 20 rebars around the concrete core. The test results from 25 specimens out of the 41 circular tubular steel columns were used in this study. Figure 7 shows correlations between the calculated results and the experimental load-deflection responses for several specimens. Figures 8(a)-(b) show the phenomenon that was observed by other researchers in the columns subjected initially to double-curvature (or axial compressive load with opposite eccentricities at the ends) of an instability or abrupt change in the deflected shape to a more stable single-curvature shape. The anti-symmetric deformed shape (double-curvature) of the column is maintained only up to a certain value of the applied eccentric axial load. However, the proposed model does not capture the phenomenon of instability in the deflected shape, because it assumes a perfectly anti-symmetric moment diagram and consequently a double-curvature deformed shape at all load levels. To capture this phenomenon, the numerical process must be capable of predicting any change in the deflected shape of the column (i.e., it must be controlled by deflection rather than by load).
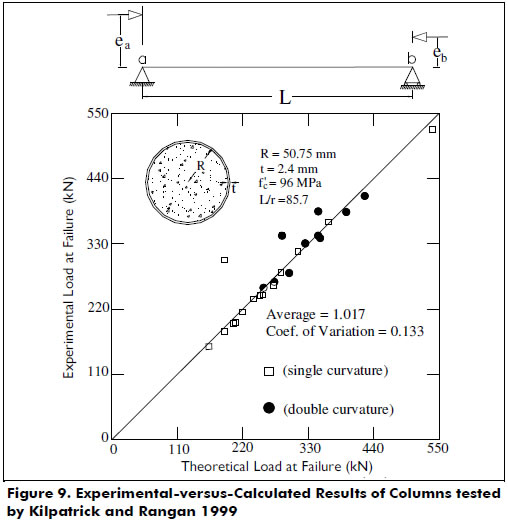
Table 4 shows the applied end eccentricities ea and eb, and the experimental and theoretical axial load values at failure, and Figure 9 shows the correlation between these axial load values.
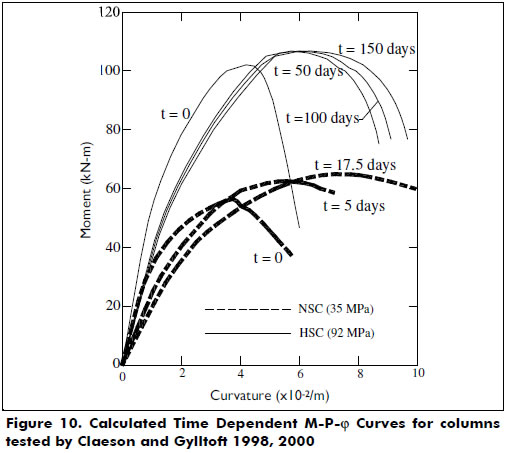
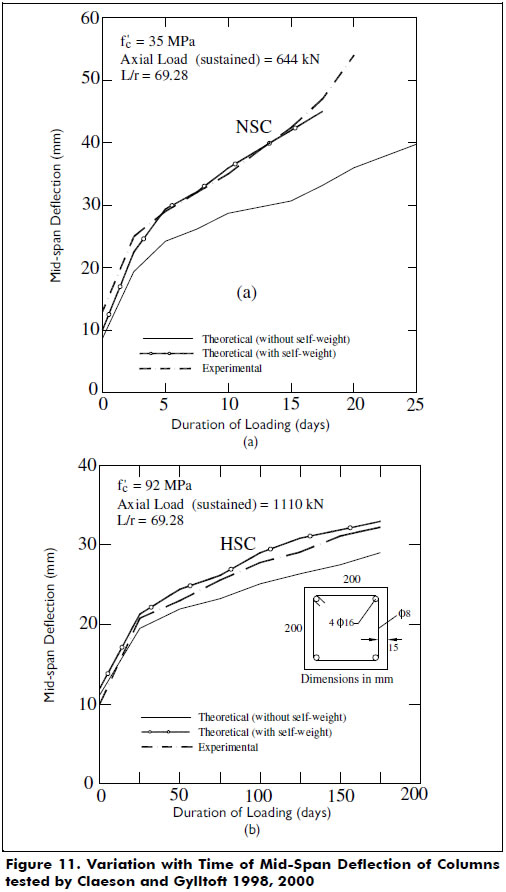
Columns tested by Claeson and Gylltoft 1998, 2000-. Slender columns made of HSC and normal strength concrete (NSC) subjected to long-term loadings (i.e., sustained loads) were tested. All column specimens had a span length of 4 m. To take into account the long-term effects of creep and shrinkage in the concrete, the creep coefficient proposed by Han [6], χ = 1 and the expression: εsh(t) = 0.004t/(t + 35) (ACI 209 Committee) for shrinkage strain in the concrete were utilized in the proposed method. Because all columns were tested horizontally, the analysis also included the transverse deflections caused by the weight of the columns. Figure 10 shows the calculated (theoretical) M-P-φ curves used in the analysis. Figure 11 shows good agreement between the calculated and experimental curves.
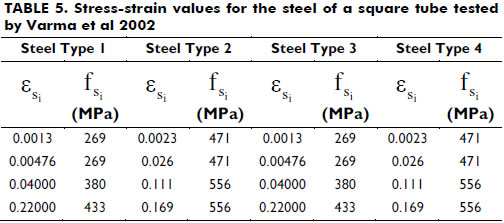
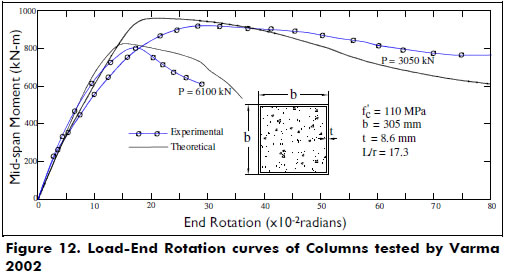
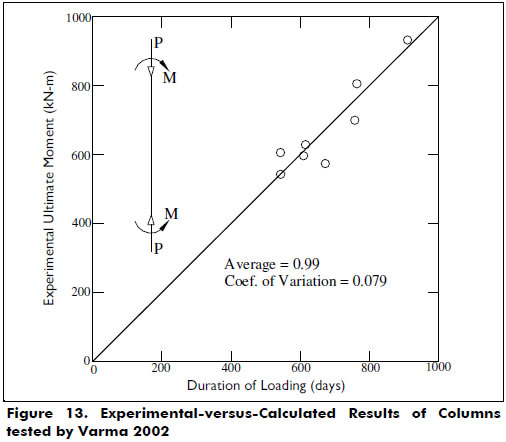
Columns tested by Varma et al 2002-. A series of columns made of square 305-mm steel tubes of 8.9 and 5.8 mm in thickness filled with high strength concrete fc' = 15,954 psi (110 MPa) and with a height of 59.84 in. (1.52 m) were tested. The column specimens were made of four types of steel, as indicated in Table 5. All column specimens were tested under short-term loads with an increasing bending moment up to failure and at a constant axial load P. Figure 12 shows the predicted end rotations at various axial load levels. To obtain the rotation along the descending part of the end moment-rotation curve for a given value of P, the ascending value of the rotation was multiplied by L/π. Figure 13 shows good agreement between the experimental and the theoretical values of the moments at failure.
Conclusions
The validity of the proposed method and numerical algorithm was tested against experimental results reported by different researchers of over seventy column specimens. The proposed method can be used to analyze any prismatic slender beam-column, including those made of a solid or hollow (rectangular, circular, oval, C-, T-, L-, or any arbitrary shape) cross section and of beam-columns made of circular and rectangular steel tubes filled with HSC.
Acknowledgements
This paper is based on research sponsored by DIME and the Civil Engineering School of the National University of Colombia at Medellín. The authors appreciate their support.
References
Cederwall, K., Engstrom, B., & Grauers, M. (1990). High-Strength Concrete used in composite columns. ACI, (SP-121), 195-214. [ Links ]
Claeson, C., & Gylltoft, K. (2000). Slender Concrete Column Subjected to Sustained and Short-Term Eccentric Loading. ACI structural J., 97(1), 45-52. [ Links ]
Hsu, C-T. T., Hsu, L. S. M., & Tsao, W-H. (1995). Biaxially Loaded Slender High-Strength Reinforced Concrete with and without Steel Fibres. Magazine of concrete Research, 47(173), 299-310. [ Links ]
Kilpatrick, A. E., & Rangan, B. V. (1999). Test on High-Strength Concrete-Filled Steel Tubular Columns. ACI structural J., 96(2), 268-274. [ Links ]
Lloyd, N. A., & Rangan, B. V. (1996). Studies on High Strength Concrete Columns under Eccentric Compression. ACI Structural J., 93(6), 631-638. [ Links ]
Rodriguez-Gutierrez, J. A., & Aristizabal-Ochoa, J. D. (2014). Biaxial bending of slender HSC columns and tubes filled with concrete under short and long term loads: I) Theory. Ingeniería e Investigación, 34(2), 23-28. [ Links ]
Varma, A. H., Ricles, J. M., Sause, R., & Lu, L. (2002). Experimental Behavior of High Strength Square Concrete-Filled Steel Tube Beam-Columns. J. Struct. Engrg., 128(3), 309-318. [ Links ]













