Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Ingeniería e Investigación
versão impressa ISSN 0120-5609
Ing. Investig. vol.34 no.3 Bogotá sep./dez. 2014
https://doi.org/10.15446/ing.investig.v34n3.44721
DOI: http://dx.doi.org/10.15446/ing.investig.v34n3.44721
O. Chiavone-Filho1, E. L. Foletto2 and L. R. Terron3
1 Osvaldo Chiavone-Filho. Chemical Enginner, PhD. Affiliation: Titular Professor, Department of Chemical Engineering, Federal University of Rio Grande do Norte, Brazil. E-mail: osvaldochiavonefilho@gmail.com
2 Edson Luiz Foletto. Chemical Enginner, Dr. Affiliation: Associate Professor, Department of Chemical Engineering, Federal University of Santa Maria, Brazil. E-mail: efoletto@gmail.com
3 Luiz Roberto Terron. Chemical Enginner, Dr. Affiliation: Associate Professor, Department of Chemical Engineering, University of São Paulo, Brazil. E-mail: lrterron@usp.br
How to cite: Chiavone-Filho, O., Foletto, E., & Terron, L. R. (2014). Representation of phase equilibria and densities for complex systems using a van der Waals volume translated equation of state with a UNIFAC mixing rule. Ingeniería e Investigación, 34(3), 26-30.
ABSTRACT
This work investigated the applicability of the van der Waals cubic equation of state (EoS) with volume translation (vdWt), using the modified Huron-Vidal (MHV2) mixing rule with the UNIFAC (UNIQUAC Functional Activity Coefficients) model for describing phase equilibrium and density data for a series of complex systems over wide ranges of temperature (T) and pressure (P). Some limitations were identified in the prediction of the experimental data collected, e.g., systems with highly associating components, but in general, the EoS vdWt+MHV was able to satisfactorily represent both phase equilibrium and volumetric behavior.
Keywords: Phase equilibrium, equation of state, mixing rule, volume translation, UNIFAC.
RESUMEN
En este trabajo se investigó la aplicabilidad de la ecuación de estado cúbica, de Van der Waals, con translación en volumen (vdWt). Para la regla de mezcla, se aplicó el método de Huron-Vidal modificado (MHV2), con el modelo UNIFAC (UNIQUAC funcional coeficiente de actividad) para describir datos del equilibrio de fases y la densidad para una serie de sistemas complejos; en amplias gamas de temperatura (T) y presión (P). Se encontraron algunas limitaciones en la predicción de los datos experimentales recogidos, por ejemplo, en los sistemas con componentes altamente asociativos, la ecuación vdWt+MHV demostró capacidad para representar de manera satisfactoria, tanto el equilibrio de fases como el comportamiento volumétrico.
Palabras clave: equilibrio de fases, ecuación de estado, regla de mezcla, traslación en volumen y UNIFAC.
Received: August 1st 2014 Accepted: September 5th 2014
Introduction
UNIFAC is a group contribution activity coefficient model whose application as a mixing rule results in a predictive equation of state (EoS) for the desired thermodynamic properties, i.e., density, enthalpy, and phase equilibrium. It is important to note that an EoS may be applied over wide ranges of temperature (T) and pressure (P), which is not possible using activity coefficient models such as UNIFAC because these models are limited by the conditions of the experimental data from which their parameters are estimated, normally low pressures and subcritical components. On the other hand, activity coefficient models are characterized by their capability to describe phase equilibrium data for complex systems due to their mathematical flexibility. Thus, a cubic and simple EoS, combined with the UNIFAC model via the mixing rule, may provide the required tool for predicting thermodynamic properties valid for various classes of mixtures as well as for wide ranges of T and P. Mixing rules for cubic EoS using group contribution excess free energy models have been studied by various researchers, including Twu et al. (1998), Heidemann (1996), Orbey and Sandler (1996), Novenario et al. (1996), Kalospiros et al. (1995), Kontogeorgis and Folas (2010), Haghtalab and Mahmoodi (2010), Staud and Soares (2012), and Costa et al. (2014). The modified Huron-Vidal mixing rule was introduced by Michelsen (1990), properly matching the excess Gibbs energy calculated by the EoS at zero pressure. This procedure allows for the use of the existing parameters of activity coefficient models that are usually based on experimental data gathered at low pressure.
In this study, the MHV2 mixing rule for the vdW EoS is combined with the UNIFAC model. Several versions of the UNIFAC model have been used according to the system studied, i.e., original (Hansen et al., 1991), modified (Larsen et al., 1987) and gas-solvent group (Dahl et al., 1991).
The translation in volume also constitutes an extension of the cubic EoS by an implementation of a volumetric dependency. It is shown in this study that the translated vdW EoS significantly improves the representation of saturated liquid densities. Furthermore, the translation does not affect the phase equilibrium calculation (Péneloux et al., 1982, Meyer, 1987, Tsai and Chen, 1998, Wang and Gmehling, 1999). On the other hand, the calculation of mixture-saturated densities depends on the energy parameter and thereby on the mixing rule adopted, which in this study is the MHV2 mixing rule.
This aim of this work is to systematically evaluate the applicability of the vdWt EoS using the MHV2 mixing rule with UNIFAC for representing phase equilibrium and density data for various complex systems over wide ranges of T and P.
Thermodynamic model
The vdWt EoS is used to represent the desired properties.
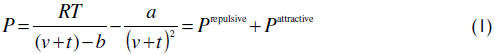
The pure component parameters are calculated from the critical properties according to equation (2).
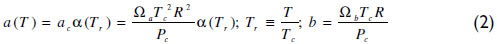
α is a function of the reduced temperature (Tr). Equation (3) shows the Soave expression applied, where ω is the acentric factor. For subcritical conditions, the Mathias and Copeman (1983) function has been used with coefficients fitted to match the vapor pressure curve; see equation (4) and Table 1.
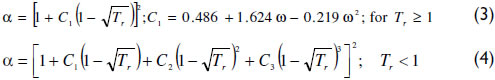
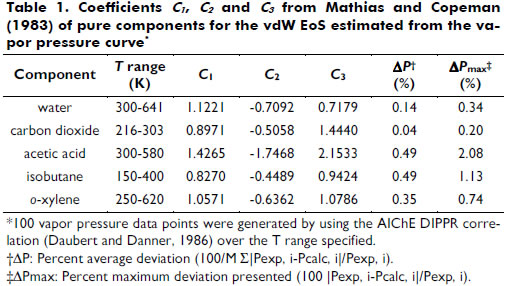
It is noteworthy that the vdW yields the same degree of vapor pressure correlation as the Peng-Robinson (PR) and Soave-Redlich-Kwong (SRK) EoS (Meyer, 1987). This suitable representation of the vdW EoS has also been observed for 438 components (Chiavone-Filho et al., 2001).
The translation function t used herein was developed based on a series of organic and inorganic species of liquid molar volume data and is described as follows (Terron, 2009).
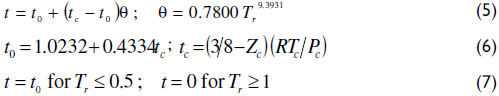
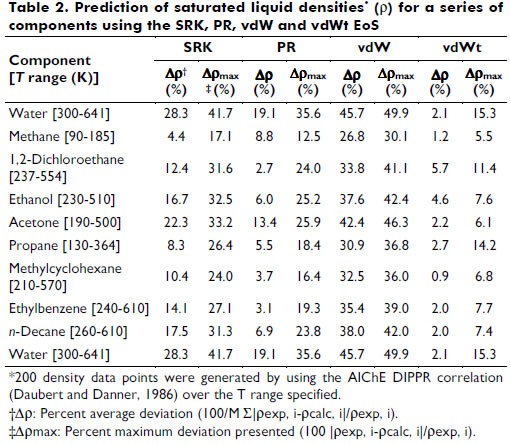
Table 2 shows the predicted saturated liquid densities for a series of components with four cubic EoS, where the vdWt representation of the experimental points is emphasized.
The mixing rules define how the EoS parameters are calculated as a function of composition. For the translation (t) and the covolume (b) parameters, the simple linear mixing rule is adequate.

For the attractive parameter (a), the conventional quadratic mixing rule presents limitations for systems of species with asymmetry in terms of size, shape and polarity. Michelsen (1990) successfully modified the mixing rule of Huron and Vidal from an infinite-reference pressure to a zero-reference pressure using a function q of the EoS parameters.
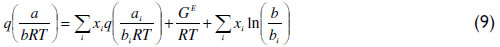
This q function provides the adequate matching procedure for the application of the Huron-Vidal mixing rule using activity coefficient models. As explained in the literature (Michelsen, 1990; Dahl and Michelsen, 1990), the function q in its original form presents discontinuities for values of a/(bRT) lower than 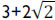 . To overcome this limitation, a linear correlation of q was proposed using phase equilibrium data at low pressure in the range of ai/(biRT) values between 7 to 9 for the vdW EoS. More recently, Dahl et al. (1991) applied a quadratic q function, introducing the so-called MHV2 model. In this work, MHV2 is applied for the vdW EoS with the following estimated parameters: q1=-0.6731 and q2=-0.0112. Equation (10) describes the MHV2 for the mixture parameter a, which is an implicit expression,
. To overcome this limitation, a linear correlation of q was proposed using phase equilibrium data at low pressure in the range of ai/(biRT) values between 7 to 9 for the vdW EoS. More recently, Dahl et al. (1991) applied a quadratic q function, introducing the so-called MHV2 model. In this work, MHV2 is applied for the vdW EoS with the following estimated parameters: q1=-0.6731 and q2=-0.0112. Equation (10) describes the MHV2 for the mixture parameter a, which is an implicit expression,
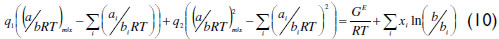
Methods of calculation
The isofugacity equilibrium criterion is applied via the phi-phi approach, one model for both phases.

Two types of phase equilibrium calculations were used. The Bubble P calculation is the one in which xi and T are given and yi and P are determined. In the PT-FLASH mode (Michelsen, 1982; Michelsen and Mollerup, 2007), T, P and zi (feed concentration) are given to determine xi and yi and the concentrations of the two phases. The PT-FLASH routine is also applied for liquid-liquid calculation.
The saturated liquid densities are calculated after the determination of the roots of the cubic EoS and are corrected by translation.

Results and final remarks
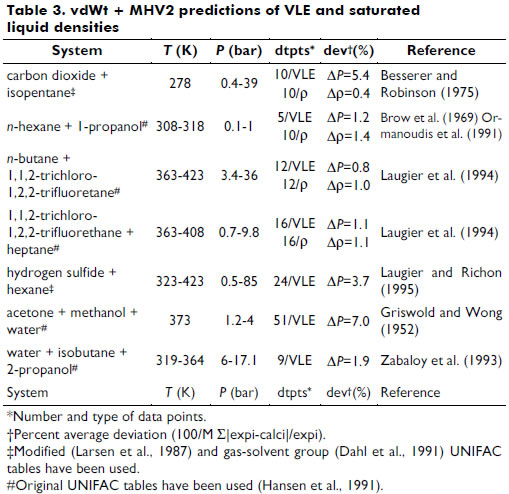
A representative series of experimental data for vapor-liquid equilibrium (VLE) and saturated liquid density (r) were selected for various systems and conditions to evaluate the prediction ability of the present vdWt+MHV2 EOS; see Table 3.
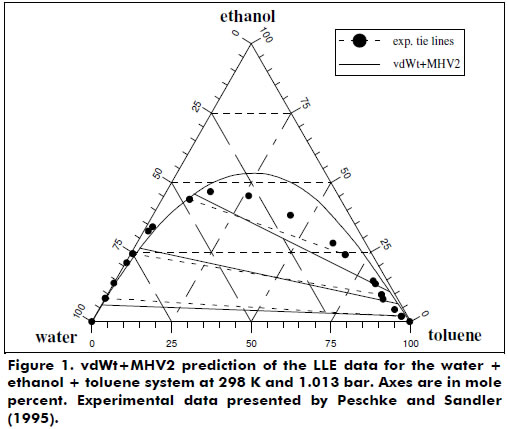
Liquid-liquid equilibrium (LLE) data representation for some ternary systems, such as water + acetic acid + isoamyl alcohol, was also studied. Figure 1 demonstrates the LLE behavior predicted by the vdWt+MHV2 for the mixture water + ethanol + toluene, which is as good as the UNIFAC (Peschke and Sandler, 1995).
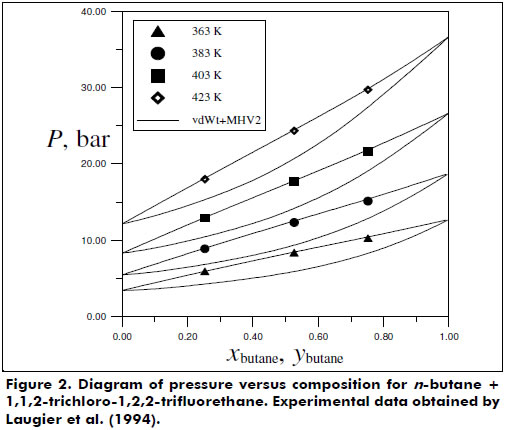
Figures 2 and 3 present the good phase equilibrium and density data predictions yielded by the vdWt+MHV2 EoS for the butane + 1,1,2-trichloro-1,2,2-trifluorethane system. The H2S + hexane system was also studied under supercritical conditions, and the vdWt+MHV2 EoS was determined to provide satisfactory representation; see Figure 4.
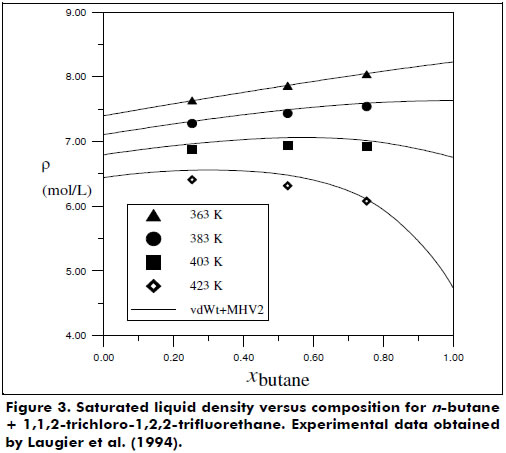
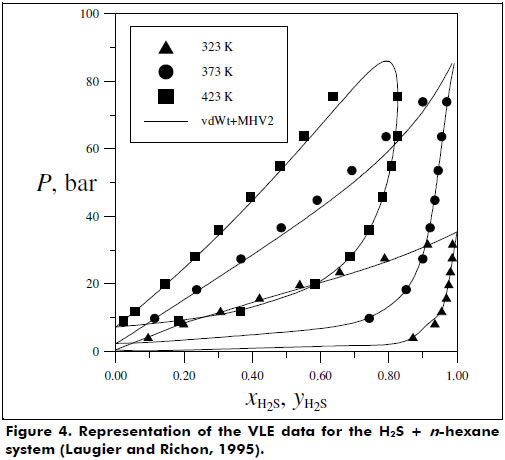
Some limitations in the prediction of the experimental data collected were identified, e.g., systems with highly associative components and with significant asymmetry. In particular, the systems carbon dioxide + isopentane and acetone + methanol + water presented higher deviations for the vdWt+MHV2 VLE data description. For the liquid density representation, polar species such as 1,2-dichloroethane and ethanol showed more pronounced deviations from the vdWt EoS. To overcome these limitations, association and more rigorous repulsive terms should be considered in the thermodynamic model (Kalospiros et al., 1995; Kontogeorgis and Folas, 2010). However, in general, the EoS vdWt+MHV2 was able to satisfactorily represent both phase equilibrium and volumetric behavior. The translation in volume expression proposed in this work can be extended to a more comprehensive series of pure substances using available data. In addition, it would be advantageous to have a continuous translation function, valid for wide ranges of T and P. The mixing rule is limited to the UNIFAC parameters; however, as shown by Dahl et al. (1991) and more recently by Haghtalab and Mahmoodi (2010), interaction parameters for supercritical components can be estimated by correlating gas solubility data, thereby extending the application of the EoS. The flexibility and predictive character of the vdWt+MHV2 is found to be a simple but powerful simple tool for calculating thermodynamic properties. Furthermore, the vdWt+MHV2 may be applied in a process simulator.
Acknowledgment
Brazilian financial support provided by ANP, Petrobras, FAPESP, CAPES, CNPq and INCT of Environmental Studies is gratefully acknowledged.
Nomenclature
AIChE American Institute of Chemical Engineers
a - Attractive parameter
b - Covolume parameter
a/(bRT) - Dimensionless parameter; argument of the q function in equation (9)
Ci - Mathias and Copeman (1983) coefficients to express a as a function of the reduced temperature, see equation (4)
Dev - Deviation
DIPPR - Design Institute for Physical Properties
dtpts - Number and type of data points, see Table 3
EoS - Equation(s) of State
G - Gibbs free energy
LLE - Liquid-liquid equilibrium
MHV2 - Modified Huron-Vidal mixing rule with quadratic approximation for the q function
M - Total number of data points
N - Total number of components
P - Pressure
PR - Peng-Robinson
q - Function of ai/(biRT) in the MHV mixing rule
qi - Coefficients of the q function in the MHV mixing rule
R - Universal gas constant
SRK - Soave-Redlich-Kwong
T - Absolute temperature
t - Translation parameter or function
ti - Translation coefficients, see equations (5) and (6)
v - Molar volume
vdW - van der Waals
vdWt - van der Waals translated or with volume translation
VLE - Vapor-liquid equilibrium
x - Mole fraction of the liquid phase
y - Mole fraction of the vapor phase
Z - Compressibility factor
z - Mole fraction of the feed in the Flash calculation
Greek Letters
α - Alpha function expressing the dependence of the attractive parameter on the reduced temperature; see equation (4)
ρ - Liquid molar density
φ - Fugacity coefficient
θ - Theta function expressing the dependence of the translation parameter on the reduced temperature; see equation (5)
ω - Acentric factor
Superscripts and Subscripts
c - Critical property
calc - Calculated value
E - Excess property
exp - Experimental value
L - Liquid phase
max - Maximum
r - Reduced property
V - Vapor phase
^ - Property of component i in the mixture
References
Besserer, G. J., & Robinson, D. B. (1975). Equilibrium-phase properties of isopentane-carbon dioxide. Journal of Chemical and Engineering Data, 20, 93-96. [ Links ]
Brow, I., Fock, W., & Smith, F. (1969). The thermodynamic properties of solutions of normal and branched alcohols in benzene and n-hexane. Journal of Chemical Thermodynamics, 1, 273-291. [ Links ]
Chiavone-Filho, O., Filho, P. G. A., Silva, D. N., & Terron, L. R. (2001). A function for a series of hydrocarbons to Peng-Robinson and van der Waals equations of state. Industrial and Engineering Chemistry Research, 40, 6240-6244. [ Links ]
Costa, G. M. N., Cardoso, S. G., Soares, R. O., Santana, G. L., & Melo, S. A. B. V. (2014). Modeling high pressure vapor-liquid equilibrium of ternary systems containing supercritical CO2 and mixed organic solvents using Peng-Robinson equation of state. Journal of Supercritical Fluids, 93, 82-90. [ Links ]
Dahl, S., Fredenslund, A., & Rasmussen, P. (1991). The MHV2 model: a UNIFAC-based equation of state model for prediction of gas solubility and vapor-liquid equilibria at low and high pressures. Industrial and Engineering Chemistry Research, 30, 1936-1945. [ Links ]
Dahl, S., & Michelsen, M. (1990). High-pressure vapor-liquid equilibrium with a UNIFAC-based equation of state. AIChE Journal, 36, 1829-1836. [ Links ]
Daubert, T. E., & Danner, R. P. (1986). DIPPR data compilation. New York: AIChE. [ Links ]
Griswold, J., & Wong, S. Y. (1952). Phase-equilibria of the acetone-methanol-water system from 100 oC into the critical region. Chemical Engineering Progress Symposium Series, 48(3), 18-34. [ Links ]
Haghtalab, A., & Mahmoodi, P. (2010). Vapor-liquid equilibria of asymmetrical systems using UNIFAC-NRF group contribution activity coefficient model. Fluid Phase Equilibria, 289, 61-71. [ Links ]
Hansen, H. K., Rasmussen, P., Fredenslund, A., Schiller, M., & Gmehling, J. (1991). Vapor-liquid equilibria by UNIFAC group contribution. 5. Revision and Extension. Industrial and Engineering Chemistry Research, 30, 2352-2355. [ Links ]
Heidemann, R. A. (1996). Excess free energy mixing rules for cubic equations of state. Fluid Phase Equilibria, 116, 454-464. [ Links ]
Kalospiros, N. S., Tzouvaras, N., Coutsikos, P., & Tassios, D. P. (1995). Analysis of zero-reference-pressure EoS/GE models. AIChE Journal, 41(4), 928-937. [ Links ]
Kontogeorgis, G. M., & Folas, G. K. (2010). Thermodynamic models for industrial applications: from classical and advanced mixing rules to association theories. Chichester, United Kingdom: John Wiley & Sons Ltd. [ Links ]
Larsen, B. L., Rasmussen, P., & Fredenslund, A. (1987). A modified UNIFAC group-contribution model for prediction of phase equilibria and heats of mixing. Industrial and Engineering Chemistry Research, 26, 2274-2286. [ Links ]
Laugier, S., Richon, D., & Renon, H. (1994). Bubble curves and saturated liquid molar volumes for chlorofluorohydrocarbon-hydrocarbon mixtures. Experimental data and modeling. Journal of Chemical and Engineering Data, 39, 166-171. [ Links ]
Laugier, S., & Richon, D. (1995). Vapor-liquid equilibria for hydrogen sulfide + hexane, + cyclohexane, + benzene, + pentadecane, and + (hexane + pentadecane). Journal of Chemical and Engineering Data, 40, 153-159. [ Links ]
Mathias, P. M., & Copeman, T. W. (1983). Extension of the Peng-Robinson equation of state to complex mixtures: evaluation of the various forms of local composition concept. Fluid Phase Equilibria, 13, 91-108. [ Links ]
Michelsen, M. L. (1990). A modified Huron-Vidal mixing rule for cubic equations of state. Fluid Phase Equilibria, 60, 213-219. [ Links ]
Michelsen, M. L., & Mollerup, J. (2007). Thermodynamic models: fundamentals and computational aspects (2nd ed.). Holte, Denmark: Tie-Line Publications. [ Links ]
Michelsen, M. L. (1982). The isothermal flash problem. Part 2. Phase split calculation. Fluid Phase Equilibria, 9, 21-40. [ Links ]
Novenario, C. R., Caruthes, J. M., & Chao, K. C. (1996). A mixing rule to incorporate solution model into equation of state. Industrial and Engineering Chemistry Research, 35, 269-277. [ Links ]
Orbey, H., & Sandler, S. I. (2004). Analysis of excess free energy based equations of state models. AIChE Journal, 42(8), 2327-2334. DOI: 10.1002/aic.690420822. [ Links ]
Ormanoudis, C., Dakos, C., & Panayiotou, C. (1991). Volumetric properties of binary mixtures. 2. Mixtures of n-hexane with ethanol and 1-propanol. Journal of Chemical and Engineering Data, 36, 39-42. [ Links ]
Péneloux, A., Rauzy, E., & Fréze, R. (1982). A consistent correction for Redlich-Kwong-Soave volumes. Fluid Phase Equilibria, 8, 7-23. [ Links ]
Peschke, N., & Sandler, S. I. (1995). Liquid-liquid equilibria of fuel oxygenate + water + hydrocarbon mixtures. Journal of Chemical and Engineering Data, 40, 315-320. [ Links ]
Staudt, P. B., & Soares, R. P. (2012). A self-consistent Gibbs excess mixing rule for cubic equations of state. Fluid Phase Equilibria, 334, 76- 88. [ Links ]
Meyer, E. C. (1987). Using Vapor Pressure Information in a Cubic Equation of State. AIChE Journal, 33, 503-505. [ Links ]
Michelsen, M. L., & Mollerup, J. (2007). Thermodynamic models: fundamentals and computational aspects. (2nd ed.) Holte, Denmark: Tie-Line Publications. [ Links ]
Terron, L. R. (2009). Termodinâmica Química Aplicada (1st ed.). Barueri, São Paulo, Brazil: Manole. [ Links ]
Tsai, J. C., & Chen, Y. P. (1998). Application of a volume-translated Peng-Robinson equation of state on vapor-liquid equilibrium calculations. Fluid Phase Equilibria, 145, 193-215. [ Links ]
Twu, C. H., Coon, J. E., & Bluck, D. (1998). A zero-pressure cubic equation of state mixing rule for predicting high pressure phase equilibria using infinite dilution activity coefficient at low temperature. Fluid Phase Equilibria, 150-151, 181-189. [ Links ]
Wang, L. S., & Gmehling, J. (1999). Improvement of the SRK equation of state for representing volumetric properties of petroleum fluids using Dortmund Data Bank. Journal of Chemical Engineering Science, 54, 3885-3892. [ Links ]
Zabaloy, M. S., Mabe, G. D. B., Bottini, S. B., & Brignole, E. A. (1993). Vapor-liquid equilibria in ternary mixtures of water-alcohol-non polar gases. Fluid Phase Equilibria, 83, 159-166. [ Links ]













