Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.34 no.3 Bogotá Set./Dec. 2014
https://doi.org/10.15446/ing.investig.v34n3.41675
DOI: http://dx.doi.org/10.15446/ing.investig.v34n3.41675
H. F. Rueda1, A. Parada2 and H. Arguello3
1Hoover Fabián Rueda Chacon. Bachelor of Sciences in Computer Science, Master of Sciences in Computer Science and Informatics, Universidad Industrial de Santander, Colombia. Affiliation: Ph. D. student in Electrical and Computer Engineering at the University of Delaware, USA. E-mail: rueda@udel.edu
2Alejandro Parada Mayorga. Bachelor of Electronic Engineering, Master of Electronic Engineering, Universidad Industrial de Santander, Colombia. Affiliation: PhD student, University of Delaware, USA. E-mail: alejopm@udel.edu
3Henry Arguello Fuentes. Electrical engineer, Master in Electrical Power, Universidad Industrial de Santander, Colombia. PhD in Electrical and Computer Engineering, University of Delaware, USA. Affiliation: Associate professor in full-time dedication of the School of Engineering and Computer Systems of the Universidad Industrial de Santander, Colombia. E-mail: henarfu@uis.edu.co
How to cite: Rueda, H. F., Parada, A., & Arguello, H. (2014). Spectral Resolution Enhancement of Hyperspectral Imagery by a Multiple-Aperture Compressive Optical Imaging System. Ingeniería e Investigación, 34(3), 50-55.
ABSTRACT
The Coded Aperture Snapshot Spectral Imaging (CASSI) system captures the three-dimensional (3D) spatio-spectral information of a scene using a set of two-dimensional (2D) random-coded Focal Plane Array (FPA) measurements. A compressive sensing reconstruction algorithm is then used to recover the underlying spatio-spectral 3D data cube. The quality of the reconstructed spectral images depends exclusively on the CASSI sensing matrix, which is determined by the structure of a set of random coded apertures. In this paper, the CASSI system is generalized by developing a multiple-aperture optical imaging system such that spectral resolution enhancement is attainable. In the proposed system, a pair of high-resolution coded apertures is introduced into the CASSI system, allowing it to encode both spatial and spectral characteristics of the hyperspectral image. This approach allows the reconstruction of super-resolved hyperspectral data cubes, where the number of spectral bands is significantly increased and the quality in the spatial domain is greatly improved. Extensively simulated experiments show a gain in the peak-signal-to-noise ratio (PSNR), along with a better fit of the reconstructed spectral signatures to the original spectral data.
Keywords: Hyperspectral imaging, Spectral resolution enhancement, Compressive sensing, Coded aperture.
RESUMEN
El sistema de sensado de imágenes espectrales, basado en la apertura codificada y de única toma (CASSI), captura la información espacial y espectral de una escena; mediante mediciones codificadas aleatorias capturadas en un sensor 2D. Un algoritmo basado en la teoría de sensado compresivo (CS), es utilizado para recuperar la escena tridimensional original a partir de las mediciones aleatorias capturadas. La calidad de reconstrucción de la escena depende exclusivamente, de la matriz de sensado del CASSI, la cual es determinada por la estructura de las aperturas codificadas que son utilizadas.
En este artículo, se propone una generalización del sistema CASSI por medio del desarrollo de un sistema óptico multi-apertura, que permite el mejoramiento de la resolución espectral. En el sistema propuesto, un par de aperturas codificadas de alta resolución es introducido en el sistema CASSI, permitiendo así, la codificación tanto espacial como espectral de la imagen hiperespectral. Este enfoque permite la reconstrucción de cubos de datos hiperespectrales, donde el número de las bandas espectrales se aumenta significativamente respecto al original, y la calidad espacial es mejorada en gran medida. Así mismo, los experimentos simulados muestran mejoramiento en la relación de pico-de-señal-a-ruido (PSNR), junto con un mejor ajuste en las firmas espectrales reconstruidas sobre los datos espectrales originales.
Palabras clave: imágenes hiperespectrales, mejora de resolución espectral, sensado compresivo y apertura codificada.
Received: January 22nd 2014 Accepted: September 2nd 2014
Introduction
Hyperspectral imaging requires sensing a large amount of spatial information across many wavelengths. Traditional hyperspectral imaging techniques scan adjacent zones of the underlying spectral scene and merge the results to construct a hyperspectral 3-Dimensional (3D) data cube. Push-broom spectral imaging sensors, for instance, capture a spectral data cube by using one FPA measurement per spatial line of the scene (Brady, D. J., 2009). Spectrometers based on optical band-pass filters need to scan the scene by tuning band-pass filters in steps (Eismann, M., 2012). These sensing techniques obey the well-known Nyquist criterion, which imposes a severe limit on the required number of samples. More specifically, these methods require scanning a number of zones linearly in proportion to the desired spatial or spectral resolution. As the desired resolution increases, the required number of samples grows considerably such that the cost of sensing a hyperspectral image is extremely high. Recently, a mathematical technique called Compressive Sensing (CS) has allowed signal sampling at rates below the Nyquist rate (Donoho, D. L., 2006). This new technique involves diverse mathematical areas, such as numerical optimization, signal processing, random matrix analysis, and statistics. The enormous potential of CS has been recently applied in areas such as microscopy, holography, tomography and spectroscopy (Willett, Marcia, and Nichols, 2011; Arguello and Arce, 2013).
This paper focuses on the application of CS in spectral imaging; this technique has been termed Compressive Spectral Imaging (CSI). CSI senses 2D coded random projections of the underlying scene such that the number of required projections is far less than those in the linear scanning case. CSI exploits the fact that hyperspectral images can be sparse in some basis representations (Candès and Tao, 2011). Formally, suppose that a hyperspectral signal 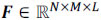 , or its vector representation
, or its vector representation 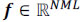 , is S-sparse on some basis Ψ, such that f = Ψθ can be approximated by a linear combination of S vectors of Ψ with S << NML. Here, N X M represents the spatial dimensions, and L is the spectral depth of the image cube. CSI allows f to be recovered from m random projections with high probability when m ≥ Slog(NML) << NML.
, is S-sparse on some basis Ψ, such that f = Ψθ can be approximated by a linear combination of S vectors of Ψ with S << NML. Here, N X M represents the spatial dimensions, and L is the spectral depth of the image cube. CSI allows f to be recovered from m random projections with high probability when m ≥ Slog(NML) << NML.
The Coded Aperture Snapshot Spectral Imaging (CASSI) system (Wagadarikar, John, Willett, and Brady, 2008; Arguello and Arce, 2011) is a remarkable imaging architecture that effectively implements CSI. Thus, CASSI senses the 3D spectral information of a scene by using 2D random projections, as depicted in Figure 1(a). The principal components in CASSI include the coded aperture, the dispersive element and the Focal Plane Array (FPA). The coded aperture patterns are the only varying elements in CASSI, while the other optical elements remain fixed during the operation of the instrument. The input-output relation in CASSI can be expressed as y = Hf, where y represents the random projections, H is the transfer function representing the dispersive element and the coded aperture effects, and f is the 3D spectral data cube in vector form (Arguello, Correa and Arce, 2013; Arguello, Rueda and Arce, 2013). Given the compressive measurement y, the objective of CS is to recover an estimate of f by using an 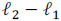 norm-based optimization algorithm, which exploits the sparsity property of the hyperspectral source.
norm-based optimization algorithm, which exploits the sparsity property of the hyperspectral source.
Despite its potential, CASSI faces a limiting trade-off between spatial and spectral resolution, with the total number of recoverable voxels constrained by the size of the FPA. This constraint limits the utility and cost-effectiveness of compressive hyperspectral imaging for many applications. CSI in infrared (IR) wavelengths is an application where FPAs are particularly critical components, because they become very costly when the resolution increases (Arce, Brady, Carin, Arguello, and Kittle, 2014). As a consequence, spectral super-resolution enhancement is a topic of high interest, because high-resolution reconstructions can be attained from low-resolution/low-cost FPA detectors.
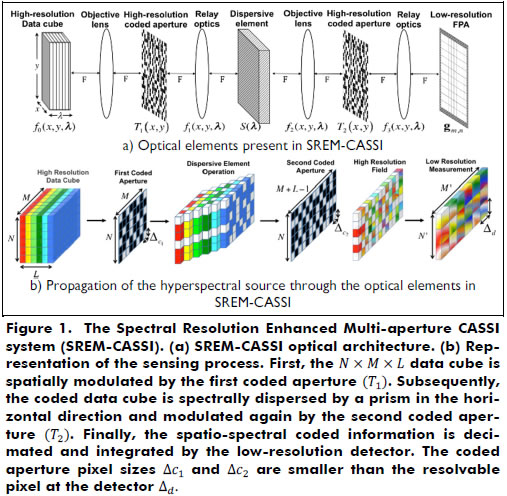
This paper presents the spectral resolution enhanced multi-aperture CASSI system (SREM-CASSI), which is a generalization of the CASSI system that includes a new multi-aperture section formed by a dispersive element sandwiched with a pair of high-resolution coded apertures. This configuration leads to multiple-coding flexibility of the spatial and spectral characteristics of the hyperspectral scene, thus permitting the reconstruction of highly resolved scenes from multiple-coded low-resolution FPA 2D projections. In particular, the random projections in SREM-CASSI are given by y = DHf, where H is the transfer function accounting for the pair of coded apertures and the dispersive element effects and D is a decimation matrix representing the effect of the low-resolution FPA detector. In the following, we introduce the design of the SREM-CASSI optical architecture, along with its optical and matrix model, as well as simulations to evaluate the attainable improvements.
SREM-CASSI System Model
The proposed SREM-CASSI optical architecture is depicted in Figure 1(a). This is composed by eight optical elements: four lenses, two high-resolution coded apertures, a dispersive element (prism or grating) and a low-resolution detector. The spatio-spectral power source density is denoted as f0(x,y,λ), where x and y index the spatial domain and λ indexes the wavelengths. The source density is first spatially modulated by the coded aperture T1(x,y), resulting in a coded field represented as f1(x,y,λ) = T1(x,y) f0(x,y,λ). Subsequently, the coded field is sheared by the dispersive element, whose output can be expressed as
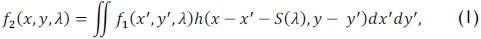
where h(x - x' - S(λ), y - y') is the optical impulse response of the system, and S(λ) represents the dispersion, which occurs only in the horizontal direction. After dispersion, the source density is then modulated by a second coded aperture T2(x,y), resulting in the field f3(x,y,λ) = T2(x,y) f2(x,y,λ).
Finally, the compressive measurements are realized by the integration of the doubly encoded and dispersed data over the detector's spectral range sensitivity. The spectral density just in front of the detector can be expressed as 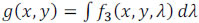 . More specifically, g(x,y) can be written as
. More specifically, g(x,y) can be written as
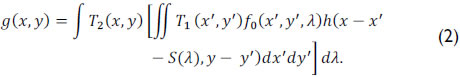
If the optical impulse response of the system is assumed to be linear, Eq. (2) can be succinctly expressed as
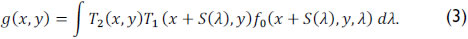
The coded aperture pixel sizes of T1 and T2 are denoted as Δc1 and Δc2, respectively. The transmittance functions of both coded apertures are then given by
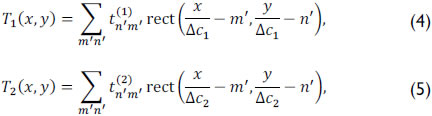
where 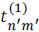 and
and 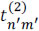 are binary values accounting for a translucent (1) or blocking (0) element. The term rect() represents the rectangular step function. In practice, the coded apertures are implemented through the use of digital micro-mirror devices (DMD) or photomasks.
are binary values accounting for a translucent (1) or blocking (0) element. The term rect() represents the rectangular step function. In practice, the coded apertures are implemented through the use of digital micro-mirror devices (DMD) or photomasks.
To choose which coded apertures to use, it is important to take care of the throughput of the system. In SREM-CASSI, the transmittances of the coded apertures define the throughput of the system; therefore, both coded apertures are related. More clearly, the transmittance of the new system is the product of the transmittance of the two coded apertures. Although the distribution of the coded aperture entries can be optimized to achieve better reconstruction results, they can be generated completely at random to show the improvement of the SREM system over the traditional CASSI. Furthermore, the use of random distributions entails high incoherence with the signal representation basis, which assures the correct reconstruction of the signal. Figure 2 shows an example of two typical coded aperture realizations with different transmittance levels, where the white pixels represent translucent elements that allow the light to pass through and the black pixels represent blocking elements.

Furthermore, assuming the pixel size of the detector is Δd, the integration of the continuous field g(x,y) in a single detector pixel can be expressed as
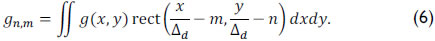
Using Eqs. (3-5) in (6), the energy captured in the (n,m)th pixel is expressed as
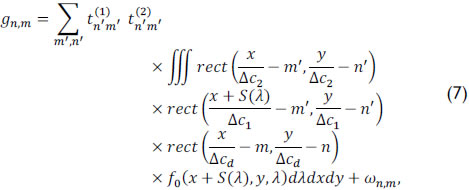
where ωn,m represents the noise of the system. Representing the source density f0(x,y,λ) in discrete form as fi,j,k, Eq. (7) can be succinctly expressed as
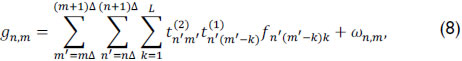
for n = 1,...,N', m = 1,...,M', where N' X M' is the number of pixels in the detector, 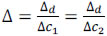 is the ratio between the size of the detector and the coded aperture pixels, and L is the number of spectral bands of the data cube. In this paper, it is assumed that
is the ratio between the size of the detector and the coded aperture pixels, and L is the number of spectral bands of the data cube. In this paper, it is assumed that 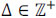 , that is, the detector and coded aperture pixel sizes satisfy Δd = k1Δc1 = k2Δc2, where k1, k2 ≥ 1 are integers. Notice that
, that is, the detector and coded aperture pixel sizes satisfy Δd = k1Δc1 = k2Δc2, where k1, k2 ≥ 1 are integers. Notice that 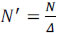 and
and 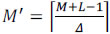 , where N X M corresponds to the number of pixels in the first coded aperture and N X (M + L - 1) in the second coded aperture. A critical requirement to achieve spectral super-resolution is that the pixel sizes of both coded apertures must be smaller than that of the detector, i.e., Δc1 < Δd and Δc2 < Δd.
, where N X M corresponds to the number of pixels in the first coded aperture and N X (M + L - 1) in the second coded aperture. A critical requirement to achieve spectral super-resolution is that the pixel sizes of both coded apertures must be smaller than that of the detector, i.e., Δc1 < Δd and Δc2 < Δd.
SREM-CASSI Matrix Forward Model
The SREM-CASSI FPA measurements given in Eq. (8) can be succinctly expressed in matrix notation as
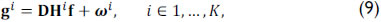
where K is the number of captured snapshots, the matrix D represents the decimation originated by the low resolution detector, gi and f are vector representations of gn,m and fijk in Eq. (8), respectively, Hi is the projection matrix accounting for the dispersive element and the ithcoded apertures, and the vector ωi represents the noise of the system. Notice that the coded apertures T1(x , y) and T2(x , y) change for every snapshot. Notice also that, in Eq. (9), f represents the high-resolution spectral source data cube, whereas the vectors gi correspond to low-resolution measurements. Figure 1(b) shows a sketch of the sensing process to obtain the low-resolution measurements gi from the high-resolution spectral scene. The snapshots are taken sequentially, and it is assumed that the underlying spectral scene remains static during the integration time of the K snapshots. The optical transmission function of the system is represented by

where P is a N(M + L - 1) X NML matrix representing the dispersive element operation and T1i and T2i are the matrix representations of the coded apertures used in the ith snapshot. Specifically, T1i is a NML X NML block-diagonal matrix of the form
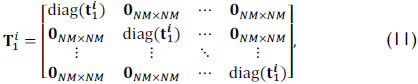
where diag(t1i) represents an NM X NM matrix with the elements of t1i in the diagonal and 0NM X NM is an zero-valued matrix. Notice that the function "diag(x)" is defined as a function that places the elements of the vector parameter x in the diagonal of a matrix.
The second coded aperture T2i operation is modeled in the system as an N(M + L - 1) X N(M + L - 1) matrix, with the values of the second coded aperture in its diagonal. Alternately, the dispersive element operation is represented by the matrix P, which can be written as
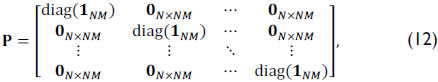
where 1NM represents an NM-long one-valued vector. Finally, d = [[1Δ 0N-Delta] ⊗ 1Delta], where ⊗ is the Kronecker matrix product operation and
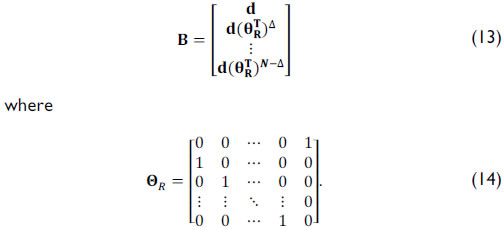
Notice that the matrix operation in Eq. 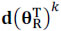 (13) shifts the columns of d by k positions circularly to the right. Consequently, the decimation operation resulting from the low-resolution detector can be modeled as
(13) shifts the columns of d by k positions circularly to the right. Consequently, the decimation operation resulting from the low-resolution detector can be modeled as
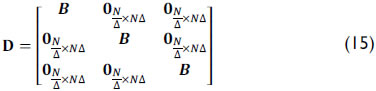
For a multiple-snapshot approach, the general model for SREM-CASSI can be written as

Furthermore, Eq. (16) can be succinctly expressed as

where H = [(H1)T ... (Hk)T]T ∈ {0,1}(N(M + L - 1)K X NML) and g = [(g1)T ... (gK)T]T. In particular for reconstruction, the hyperspectral signal 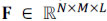 , or its vector representation
, or its vector representation 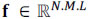 , is assumed to be S-sparse on some basis Ψ, such that f = Ψθ. Here, θ are the coefficients of the sparse representation. Hence, f can be approximated by a linear combination of S vectors from Ψ with S << N.M.L. Specifically, an estimation
, is assumed to be S-sparse on some basis Ψ, such that f = Ψθ. Here, θ are the coefficients of the sparse representation. Hence, f can be approximated by a linear combination of S vectors from Ψ with S << N.M.L. Specifically, an estimation 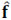 of the high-resolution data cube f from the low-resolution measurements can be achieved by solving the optimization problem
of the high-resolution data cube f from the low-resolution measurements can be achieved by solving the optimization problem
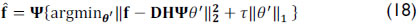
where τ > 0 is a regularization parameter that balances the conflicting tasks of minimizing the least squares residuals and, at the same time, searches for a sparse solution.
Analysis of the Forward Operators
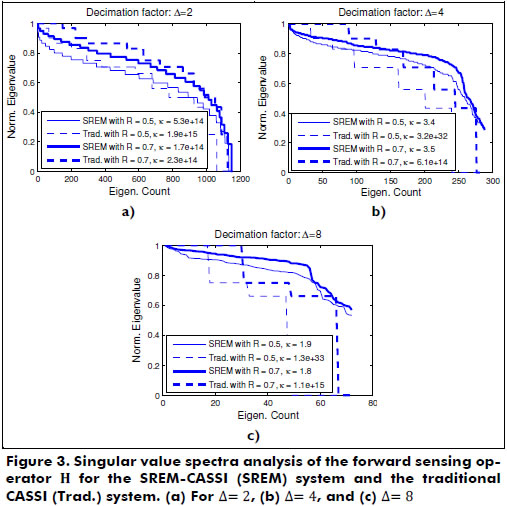
The singular value spectrums for the sensing matrices based on the random selection of the coded apertures for the SREM-CASSI system and the traditional CASSI system are presented in Figure 3. The condition number 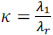 is indicated as a measure of ill-posedness, where λ1 represents the most significant eigenvalue and λr the less significant. As k is smaller, the forward operator H is better posed. It can be observed that, although the spread of the singular values behaves in a similar fashion for both architectures regardless of the transmittance level of the coded apertures, the SREM-CASSI condition number is significantly smaller than that of the traditional CASSI. In consequence, the SREM-CASSI optical design leads to better well-conditioned sensing matrices.
is indicated as a measure of ill-posedness, where λ1 represents the most significant eigenvalue and λr the less significant. As k is smaller, the forward operator H is better posed. It can be observed that, although the spread of the singular values behaves in a similar fashion for both architectures regardless of the transmittance level of the coded apertures, the SREM-CASSI condition number is significantly smaller than that of the traditional CASSI. In consequence, the SREM-CASSI optical design leads to better well-conditioned sensing matrices.
Simulations and Results
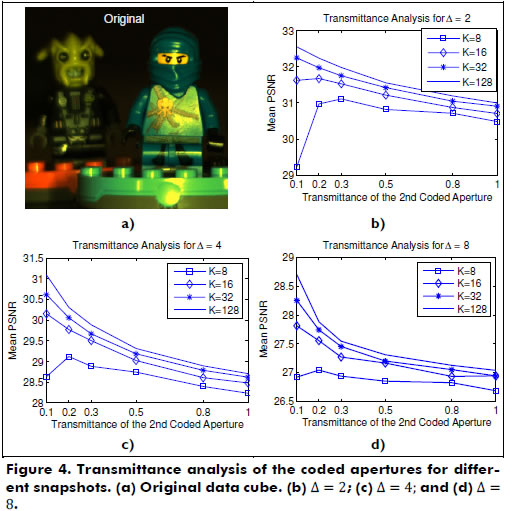
A high-resolution spectral data cube exhibiting L = 24 spectral bands and N = M = 256 spatial pixels was experimentally obtained using a wide-band Xenon lamp as light source and a visible monochromator that spans between 451 nm and 642 nm (RGB representation in Figure 4(a)). The image intensity was captured using a CCD camera with a 656x492 pixel resolution and a pixel size of 9.9 µm. A low-resolution spectral data cube was obtained by clustering the 24 bands into 6 bands. The spectral range is the same for both the high- and low-resolution data cubes. The bandwidth of each spectral band in the high-resolution data cube is 8 nm, whereas the low-resolution data cube exhibits 32 nm per band.
The goal of these experiments is to recover the datacube exhibiting 24 bands from the 6-band data cube. To accomplish this, two high-resolution coded apertures with 256x256 and 256x279 pixel resolutions are employed. The entries of these coded apertures are random realizations of Bernoulli random variables, with different levels of transmittance. To obtain an estimation of the high-resolution spectral data cube, the optimization problem in Eq. (18) is solved by using the Gradient Projection for Sparse Reconstruction algorithm (GPSR) as it exhibits faster computational speed (Figueiredo, Nowak, and Wright, 2007). In addition, the representation basis Ψ was set to be the Kronecker product of three bases, 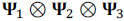 , where the combination
, where the combination 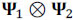 was the 2D-Wavelet Symlet 8 basis and Ψ3 was the Discrete Cosine basis. Due to the random nature of the coded aperture entries, ten trials were performed for each experiment, and the results were averaged.
was the 2D-Wavelet Symlet 8 basis and Ψ3 was the Discrete Cosine basis. Due to the random nature of the coded aperture entries, ten trials were performed for each experiment, and the results were averaged.
Three different coded aperture/detector pixel ratios Δ(2, 4, 8) were evaluated, along with six different transmittance levels (10%, 20%, 30%, 50%, 80%, and 100%) of the coded apertures. Figure 4 shows the results for different transmittance levels and the corresponding average PSNR of the reconstruction that was achieved. Note that better results are obtained when the transmittance is lower than 50%, with 10%-20% being the best average transmittance ratio interval. It can be noticed that the results worsen when we approach the CASSI architecture (transmittance = 100%).
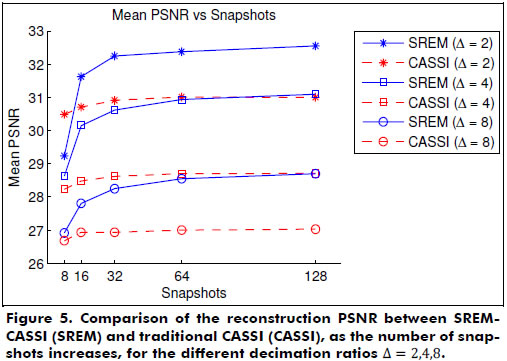
Using the best transmittance level for each experiment, Figure 5 shows the reconstruction PSNR vs. the number of captured snapshots for different values of Δ, using the SREM-CASSI and the traditional CASSI architectures. There, it is evident that, as the decimation ratio increases, the reconstruction quality decreases. However, capturing more snapshots can alleviate the loss in quality. Thus, a reconstruction PSNR of 28 dB is achieved by using either Δ = 2 and 4 snapshots, Δ = 4 and 8 snapshots, or Δ = 8 and 64 snapshots. Then, if an eight-times smaller resolution detector is available, roughly eight times more snapshots are required to achieve similar reconstruction results. In Figure 5, it can also be seen how the results from the SREM-CASSI architecture surpass those achieved by the traditional CASSI.
In contrast, Figure 6 shows the reconstruction results of the right-hand side object obtained with the traditional CASSI and the proposed architecture when Δ = 4 is used and 128 shots are captured. It can be easily noticed that the SREM reconstruction quality improves on that obtained with the traditional CASSI.

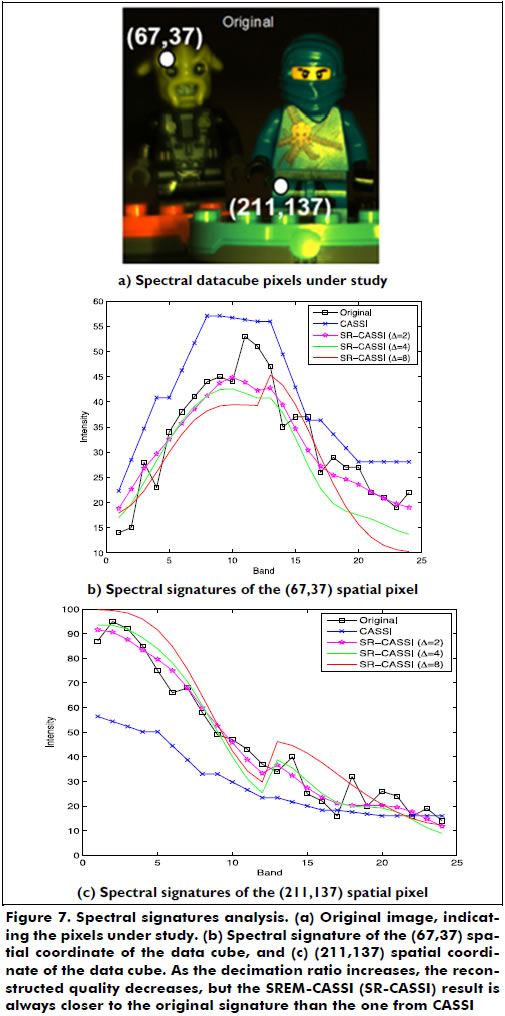
Finally, Figure 7 shows the comparison between the reconstructed spectrums of three selected points from the data cube for different number of snapshots and Δ = 2. As the number of captured snapshots increases, the spectral signatures approach the original signature.
Conclusions
A spectral resolution enhancement methodology for coded aperture-based multiple-snapshot spectral imaging systems has been developed. The proposed optical architecture exploits the sub-pixel information from the original hyperspectral signal by means of two high-resolution coded apertures, attaining richer spectral scenes by using a low-resolution detector but at the cost of capturing multiple FPA measurements. The reconstructions attained up to 32.5 dB of PSNR with half the size of a full-resolved FPA (2 dB decay), 31 dB with a detector four times smaller (3.5 dB decay) and 28.5 dB with an eight-times smaller detector (6 dB decay).
Acknowledgments
This work was partially supported by the Vicerrectoría de Investigación y Extensión of the Universidad Industrial de Santander, under the grants No. 1363, 1368, and by Colciencias and Fulbright.
References
Arce, G. R., Brady, D. J., Carin, L., Arguello, H., & Kittle D. S. (2014). An introduction to compressive coded aperture spectral imaging. IEEE Signal Processing Magazine, 31(1), 105-115. [ Links ]
Arguello, H., & Arce, G. R. (2011). Code aperture optimization for spectrally agile compressive imaging. JOSA A, 28(11), 2400-2413. [ Links ]
Arguello, H., & Arce, G. R. (2013). Rank minimization code aperture design for spectrally selective compressive imaging. IEEE Transactions on Image Processing, 22(3), 941-954. [ Links ]
Arguello, H., Correa, C., & Arce, G. R. (2013). Fast lapped block reconstructions in compressive spectral imaging. Applied Optics, 52(10), D32 - D45. [ Links ]
Arguello, H., Rueda, H., & Arce, G. R. (2013). Higher-order computational model for coded aperture spectral imaging. Applied Optics, 52(10), D12 - D21. [ Links ]
Brady, D. J. (2009). Optical Imaging and Spectroscopy. Wiley, John and Sons. [ Links ]
Candès, E., & Tao, T. (2006). Near-optimal signal recovery from random projections: Universal encoding strategies? IEEE Transactions on Information Theory, 52(12), 5406-5425. [ Links ]
Donoho, D. L. (2006). Compressed sensing. IEEE Transactions on Information Theory, 52(4), 1289-1306. [ Links ]
Eismann, M. (2012). Hyperspectral Remote Sensing. SPIE Press. [ Links ]
Figueiredo, M. A. T., Nowak, R. D., & Wright, S. J. (2007). Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems. IEEE Journal of Selected Topics in Signal Processing, 1(4), 586-597. [ Links ]
Wagadarikar, A. A., John, R., Willett, R., & Brady, D. (2008). Single disperser design for coded aperture snapshot spectral imaging. Applied Optics, 47(10), B44-B51. [ Links ]
Willett, R. M., Marcia, R. F., & Nichols, J. M. (2011). Compressed sensing for practical optical imaging systems: a tutorial. Optical Engineering, 50(7), 072601-1 - 072601-13. [ Links ]













