Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.35 no.1 Bogotá Jan.Apr. 2015
https://doi.org/10.15446/ing.investig.v35n1.42220
DOI: http://dx.doi.org/10.15446/ing.investig.v35n1.42220
C. A. Graciano1 and D. G. Zapata-Medina2
1Carlos Alberto Graciano Gallego. Ph. D., Universidad Nacional de Colombia, Medellín, Colombia. Affiliation: Associate professor, Universidad Nacional de Colombia, Medellín, Colombia. E-mail: cagracianog@unal.edu.co
2David Guillermo Zapata Medina. Ph. D., Universidad Nacional de Colombia, Medellín, Colombia. Affiliation: Assistant profesor, Universidad Nacional de Colombia, Medellín, Colombia. E-mail: dgzapata@unal.edu.co
How to cite: Graciano, C. A., & Zapata, D. G. (2015). Effect of longitudinal stiffening on bridge girder webs at incremental launching stage. Ingeniería e Investigación, 35(1), 24-30. DOI: http://dx.doi.org/10.15446/ing.investig.v35n1.42220
ABSTRACT
Patch loading is a predominant load case at incremental bridge launching. Bridge girder webs are frequently provided with longitudinal stiffeners to increase in-service shear and bending strength, and its effect has been included in design codes. However, no straightforward rules are given to account for the influence of such stiffeners on improving the patch loading resistance. This paper presents a review of some available formulae found in the literature to estimate the girder ultimate strength including the provisions of the European, American and Colombian design codes. Additionally, a nonlinear finite element analysis is conducted on three case studies related to actual launched bridges. The case studies are also used to study the influence of the longitudinal stiffener and girder depth on the girder capacity. Different load-displacement responses are observed depending on the girder depth. Finally, the finite element analysis shows to what extent the longitudinal stiffeners can increase the patch loading capacity of bridge girder webs during launching.
Keywords: Patch loading, longitudinal stiffeners, ultimate strength, girders, bridge launching, finite element method.
RESUMEN
Cargas concentradas son normalmente la condición de carga predominante durante el lanzamiento de puentes por empujes sucesivos, por lo cual, las almas de las vigas del puente son frecuentemente rigidizadas con placas longitudinales para incrementar la resistencia de servicio a cortante y flexión. Este efecto benéfico del rigidizador longitudinal es tomado en cuenta por varios códigos de diseño. Sin embargo, no hay normas claras que indiquen como tener en cuenta la influencia de tales rigidizadores en el incremento de la resistencia bajo cargas concentradas. Este artículo, presenta una revisión de algunas de las formulaciones disponibles en la literatura técnica para el cálculo de cargas últimas de pandeo en vigas bajo cargas concentradas incluyendo los lineamientos de los códigos de diseño Europeo, Americano y Colombiano. Adicionalmente, se presenta un análisis no lineal por elementos finitos de tres casos de estudio concernientes con el lanzamiento de puentes. Los casos de estudio son también utilizados para estudiar la influencia del rigidizador y de la profundidad de la viga en la carga última. Se observaron diferentes respuestas carga-deformación dependiendo de la profundidad de la viga y se muestra hasta qué punto los rigidizadores longitudinales pueden incrementar la capacidad de carga de vigas de puente durante su lanzamiento.
Palabras clave: cargas concentradas, rigidizadores longitudinales, resistencia última, vigas, lanzamiento de puentes, método de los elementos finitos.
Received: February 20th 2014 Accepted: September 30th 2014
Introduction
In the construction of composite bridges, incrementally launched steel bridges are commonly used (Seitz and Kuhlmann 2004; Davaine and Aribert 2005). For this technique, the bridge deck is usually cast before launching. This reduces the cost of the deck, but at the same time, increases substantially the weight during launching, therefore producing heavy concentrated loads normally referred to as patch or concentrated loading. Patch loadings are generated during bridged launching as the bridge girders move over the supports. These concentrated loads, which are transmitted to the girder (box or plate) as a support reaction through a launching shoe (see Figure 1), produce large out-of-plane deformations in the girder web, which in many cases, govern the thickness of the web.
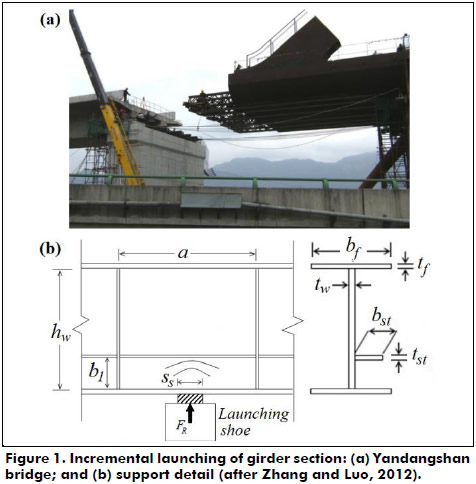
In current practice, one way to control these undesirable deformations is by providing longitudinal stiffeners to the girder web, which are primarily used in deep plate and box girders to increase bending and shear strength during in-service conditions.
The increase in web thickness and consequent increase in construction costs might be avoided by quantifying the enhancement of the patch loading resistance due to the longitudinal stiffeners. This problem has caught the attention of bridge engineering practitioners. Lagerqvist (1995) developed a design procedure based on a strength curve approach to determine the resistance to patch loading of unstiffened girders webs. Later on, Graciano (2002) proposed a methodology for the patch loading resistance of longitudinally stiffened girder webs. These procedures were introduced in the Eurocode 3 Part 1-5 (2006), covering both webs with and without transverse stiffeners and longitudinal stiffeners. Navarro et al. (2000) and Dauner et al. (2000) investigated the influence of longitudinal stiffeners for the concentrated loading case of the Vaux Viaduct.
This paper presents a review of available formulae found in the literature to estimate the girder ultimate strength and also presents finite element analyses of three case studies to show the positive effect of longitudinal stiffening on the patch loading capacity of actual bridge girder webs during launching.
Background
The presence of a longitudinal stiffener on the ultimate resistance of plate girders under concentrated loads is currently addressed in most of the design codes including the Eurocode 3. Furthermore, its effect has not yet been included in neither the American steel construction code (AISC 2010) nor the Colombian code for earthquake-resistant construction (NSR-10).
The 2006 Edition of the Eurocode 3 Part 1-5 (General rules – Plated structural elements) and Part 2 (Steel bridges) includes a check of the buckling resistance of girder webs to concentrated transverse loads at the ultimate limit load state, which is relevant during launching. More recently, several researchers have kept the interest in improving the formulation for the patch loading capacity of girder webs with longitudinal stiffeners (Seitz 2005; Davaine 2005; Clarin 2007).
In the design procedure presented in BS 5400 Part 3 (2000), the increase in the ultimate load due to the stiffener is calculated by multiplication of the ultimate load for an unstiffened girder with a magnification factor, which is function of the relative position of the stiffener. Recently, Chacón et al. (2013), showed that for several design cases the Eurocode 3 (2006) leads to underestimate results.
Laboratory tests have shown that longitudinal wed stiffening enhances the ultimate resistance of plate girders under patch loading (Bergfelt 1979, Galea et al. 1987, Shimizu et al. 1987, Janus et al. 1988, Dubas and Tschamper 1990, Markovic and Hajdin 1992, Carretero and Lebet 1998, Walbridge and Lebet 2001, Graciano and Casanova 2005, Pavlovcic et al. 2007, among others). The experimental results show an increase between 5% and 60% in ultimate loads due to the inclusion of a longitudinal stiffener.
Bergfelt (1979) proposed a semi-empirical equation for the consideration of a longitudinal stiffener in the ultimate patch load resistance of plate girders based on the regression analysis of experimental results. According to Bergfelt (1979) the ultimate load of a longitudinally stiffened girder is expressed as:
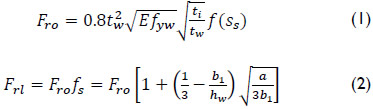
where 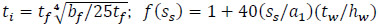 is a correction factor accounting for the influence of the patch loading length, ss; and fs is a magnification factor that accounts for the present of a longitudinal stiffener. The distance between the outermost plastic hinges in the loaded flange is:
is a correction factor accounting for the influence of the patch loading length, ss; and fs is a magnification factor that accounts for the present of a longitudinal stiffener. The distance between the outermost plastic hinges in the loaded flange is:
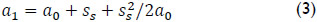
where, 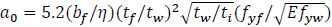 and η is a correction factor for flange bending moment (η ≈ 1).
and η is a correction factor for flange bending moment (η ≈ 1).
Kutmanova and Skaloud (1992), based on the statistical analysis of 101 experimental results for plate girders with longitudinal stiffeners tested to failure, presented a formula for fs, which only depends on the relative position of the stiffener1:
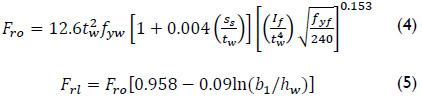
where ![]() (
(![]() ) is the moment of inertia of the flange.
) is the moment of inertia of the flange.
Markovic and Hajdin (1992) proposed a linear equation for the consideration of a longitudinal stiffener based on the statistical analysis of 133 experimental tests carried out previously by different authors.
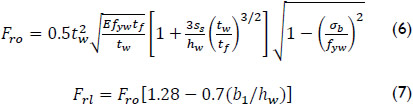
where, σb is the co-existing bending stress.
As expected, the formulas developed by Bergfelt (1979), Kutmanova and Skaloud (1992), and Markovic and Hajdin (1992) show good correlation with their own experimental results. However, they fail to capture the full range of experimental data available in the literature (Graciano 2002). Even so, Eq. (7) was incorporated in BS 5400 Part 3 (2000).
Lagerqvist and Johansson (1996) proposed that the ultimate patch load resistance for an unstiffened web can be calculated as:

where Fy is the yield resistance given as:

and χ(λ) is the resistance function expressed as:
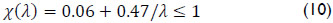
with:
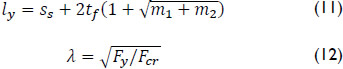
In Eqs. (11) and (12) ly is the effective loaded length; λ is the slenderness parameter; m1 and m2 are dimensionless parameters; and Fcr is the elastic buckling load.
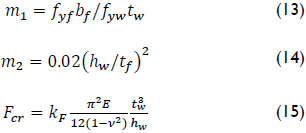
Lagerqvist (1995) proposed that for unstiffened webs the buckling coefficient, kF, can be calculated as:
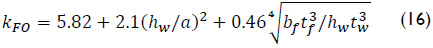
while for longitudinal stiffened plate girders kF is expressed as:

Graciano (2002) proposed that for webs with a longitudinal stiffener located within 0.05 ≤ b1/a ≤ 0.3 the contribution from the stiffener ksl to the buckling coefficient in Eq. (17) is:

where γst is the relative flexural rigidity of the longitudinal stiffener and Co is a parameter obtained by regression analysis that depends on the aspect ratio of the directly loaded subpanel and the ratio of torsional, 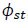 , to flexural, γst, rigidity of the longitudinal stiffener.
, to flexural, γst, rigidity of the longitudinal stiffener.
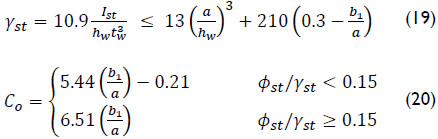
Open sections stiffeners will normally fulfill 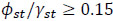 , and closed sections stiffeners
, and closed sections stiffeners 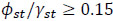 . In Eq. (17) the contribution of the longitudinal stiffener, ksl, is limited to:
. In Eq. (17) the contribution of the longitudinal stiffener, ksl, is limited to:

where γt is the transition rigidity expressed as:
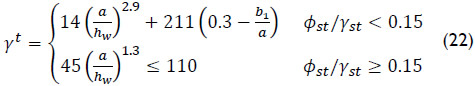
Eqs. (20) and (22) were obtained taken into account the geometric interaction between the web plate and the longitudinal stiffener. These two sets of equations also account for the transition from the global to local buckling modes.
Graciano (2001) collected 127 test results from studies carried out by different researchers. By regression analysis of these experimental results the following formula was obtained:
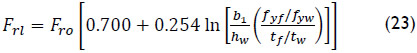
It considers the influence of a longitudinal stiffener on the ultimate capacity of patch loaded plates and takes into account for the influence of the ratio flange-to-web thickness and the difference in yield strength between flanges and web. The model presented by Graciano (2001) proposes that the ultimate load for the unstiffened web is calculated according to the model developed by Lagerqvist (1995). Results show a good correlation with the full range of experimental results used in the regression analysis.
Davaine (2005), based on an extensive FE investigation comprising 366 numerical simulations, proposes for deep plate girders some improvements to the formulation presented by Graciano (2002).
Accordingly, the critical load is calculated as:

where Fcr,1 is calculated with Eqs. (15)-(22) and the term Fcr,2 considers the buckling of the upper panel for deep girder webs according to:
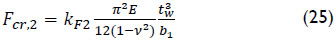
The buckling coefficient kF2 was obtained by regression analysis comprising 366 numerical simulations as:
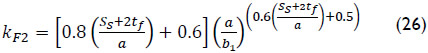
Eq. (26) is only valid when the following geometrical condition is satisfied ss + 2tf + 2b1 ≤ a.
Finally, the methodology proposed in Eurocode 3 (2006) for the ultimate resistance of girder webs under patch loading incorporates the design procedure developed by Lagerqvist and Johansson (1996) and Graciano and Johansson (2002). The ultimate load is calculated according to Eqs. (8) to (16) except that the resistance function is:

and the elastic buckling resistance, Fcr, and the buckling coefficient, kF, are simplified to:
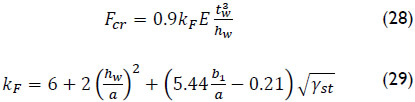
Numerical analysis
General
Implementation of nonlinear finite element analysis has been proven to be a rational tool to study the behavior of plate girders subjected to concentrated loads (Lagerqvist 1995, Granath 1998, Tryland et al. 2001, Graciano and Edlund 2002, Graciano and Casanova 2005, Graciano et al. 2011, Graciano and Ayestarán 2013). The results from the numerical analyses have shown satisfactory agreement between experimental behavior and FEM simulations. Thus, results computed by FEM analyses are reliable for the case-studies presented herein.
Description and calibration of the model
The numerical simulations were carried out herein using the multipurpose commercial FEM software ABAQUS (2011). Graciano and co-workers have already validated the finite element methodology presented herein with experimental results for patch loaded girders (Graciano et al. 2014). In summary, shell elements are used to model the girder components, additionally initial shape imperfections are assumed to have sine curves in both along and across the web plate. The loading node is placed in the plane of symmetry at the top flange, and other nodes in this flange are connected to this by nonlinear springs. Hence, the load was distributed over an area equal to the patch loading length times the flange width (ssbf). The girder material was assumed to have an ideal elastoplastic behavior. A denser mesh beneath the loaded flanged, where a significant gradient in stress distribution is expected, was employed.
Considering that the intention of this work is to analyze three case studies, the results obtained by the corresponding authors are compared to: 1) those calculated using the formulae presented herein, 2) the Eurocode 3 (2006 Edition), and 3) those obtained by the FEM analyses conducted herein. Some assumptions are correspondingly made. In general, the available formulae were developed assuming symmetry in the load and geometry of the girder, uniform thickness across and along the web. Therefore, the same assumptions were made in the FEM analyses and hence just half of the girder was modeled. In the next section the three cases-studies will be analyzed.
Case studies
Plate girders studied by Shimizu (1994)
Shimizu (1994) performed a series of numerical tests by means of the FEM. The purpose was to study the influence of a longitudinal stiffener and coexisting bending on the resistance of short plate girders subjected to patch loading. Triangular planar-shell elements and elastoplastic large deflection analysis were used in the FEM model. The model also had initial out-of-plane deflections with a sine curve in its larger subpanel. In all the models, a launching shoe is supposed to lie as a “line support”. Details of the plate girders without bending are shown in Table 1.

Material properties were taken as E = 206 GPa, v = 0.3, and the maximum out-of-plane web deflection, wo, was set to 0.6mm. The yield strength of webs and flanges was assumed to be equal to 235 MPa. Note on Table 1 that an increase of 34% in the patch loading capacity was observed when comparing the computed ultimate loads for models A300T (unstiffened) and A320T (stiffened at 0.2hw).
Figure 2 shows the load-displacement response obtained by ABAQUS for the plate girders presented in Table 1. Due to the presence of the stiffener, the load carrying capacity increases about 20% with respect to the unstiffened girder. The shadowed area represents the positive effect of the horizontal stiffener in increasing the ductility of the structure.
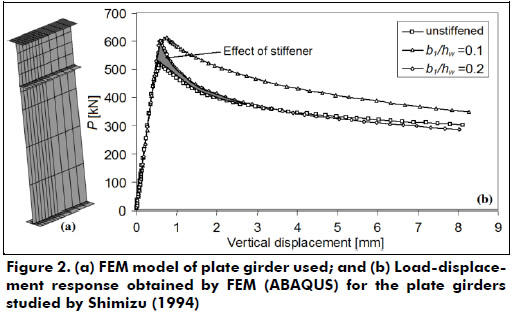
The results presented in Figure 2 are in agreement with results obtained experimentally (Galea et al. 1987, Janus et al. 1988, Tschamper et al. 1991, Wallbridge and Lebet 2001, Seitz 2005). In those works a stiffener was able to increase the patch loading capacity of the girders when placed at a position closer than 0.2hw to the loaded flange. Shimizu's analysis predicts a larger increase of the patch load resistance for girder A320T (b1 =0.2hw). It may be due to the assumption for the initial shape imperfection, where the smaller subpanel was assumed to be straight. This hypothesis can considerably affect the buckling response of the girder and consequently also the prediction of the patch loading resistance.
Part of bridge girder studied by Bergholtz (1994)
Bergholtz (1994) presented a report concerning buckling problems encountered during launching of steel bridges. Two different bridge girders were analyzed by FEM and the numerical models validated with field measurement of one I-girder web during actual bridge launching.
Figure 3 shows the dimensions one of the girders studied by Bergholtz (1994), which was also used for validation of the resistance model proposed by Lagerqvist (1998) for deep plate girders. However, for this purpose some assumptions were made. It was assumed that the girder is symmetric (a =3157 mm) and has a uniform web thickness (tw =20 mm). Additionally, the load is assumed to be applied at midplane and the girder is modeled simply supported at both ends. Taking into account the previous assumptions, the design procedure proposed by Lagerqvist (1998) gives Fro =4187 kN for an unstiffened web and without influence from the bending end moment at the girder ends. In Figure 3, the stiffener is located at about 1/4 of the girder depth.
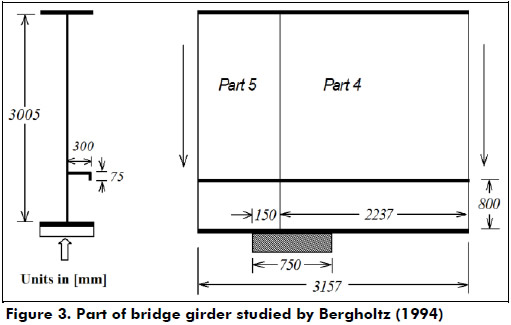

The ultimate resistance for the stiffened web computed by Bergholtz (1994) is 1.4 times higher than the one predicted by Lagerqvist (1998) for an unstiffened web. Using Eq. (22) proposed by Graciano (2001) for longitudinally stiffened girder webs an ultimate resistance Frl =5437 kN is obtained. This prediction is 7% lower than the one by Bergholtz.
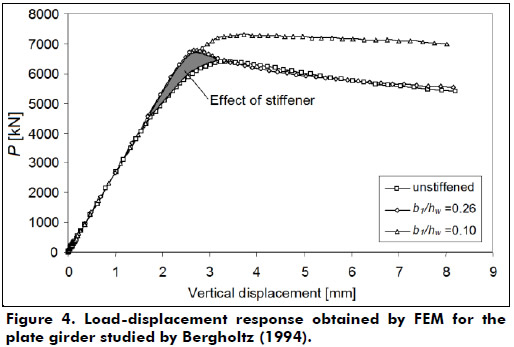
Considering similar assumptions as in the validation performed by Lagerqvist (1998) the finite element analysis made herein using ABAQUS predicts an ultimate resistance Frl =6411 kN for unstiffened web. This result is higher than the one computed by Bergholtz (1994). It must be pointed out that for the model presented herein the web thickness was assumed to be uniform with tw =20mm.
Figure 4, shows the load-deflection response of a girder similar to that studied by Bergholtz (1994). As mentioned before, symmetry in both geometry and loading conditions were considered. An additional FEM analysis was conducted where the position of the stiffener was varied. This analysis shows an increase of about 7 and 15% in ultimate loads when the stiffener is placed at 0.26hw and 0.1hw, respectively, when comparing with the unstiffened web.
Part of bridge girder studied by Dauner et al. (2000)
During the launching of the Vaux Viaduct in Switzerland some problems related to patch loading arose. It was a difficult engineering task as reported by Dauner et al. (2000) and Navarro et al. (2000). Among the problems that the designers encountered were the presence of longitudinal stiffeners, patch loading effects in a very slender girder (hw ≤ 6200 mm) and a change in the thickness along the depth of the web. The latter point is not treated in this paper. Before the launching of the viaduct, patch loading tests were conducted on 6 web panels stiffened longitudinally (Carretero and Lebet 1998). Trapezoidal stiffeners, similar to those used in the actual bridge girder, were used in the experiments.
Considering the change web thickness and the presence of closed section stiffeners some assumptions were made in order to enable the use of the aforementioned models. The assumed geometry and material properties are summarized in Table 3. In the FEM analysis conducted herein, the web thickness was assumed to be uniform and equal to 26 mm, and the stiffeners had a closed trapezoidal cross section as shown in Figure 5.

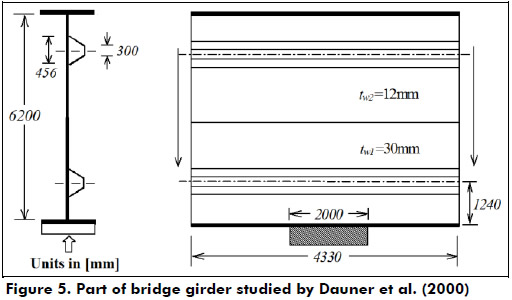
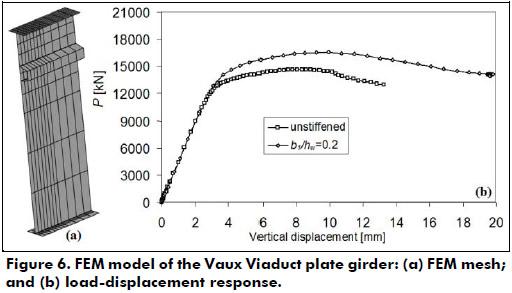
The FE model for the plate components (flanges, web and stiffener) and the load-displacement response for this plate girder are shown in Figure 6. Note that similar to other cases, the inclusion of the web stiffener increased the girder ultimate resistance by 10% with respect to the unstiffened web.
Discussion of results
Results computed by FEM analysis were shown in Figures 2, 4 and 6. In all three figures an increase in ultimate patch load is observed due to the presence of the stiffener.
For the three case-studies analyzed herein, an increase in the ductility of the plate girder is observed for the stiffener types and positions as seen in the load–displacement response of the system. The shadowed area between the curves illustrates this fact, which is also in accordance with the results obtained experimentally in the literature concerning longitudinal stiffening for patch loading. In addition, it is observed that the closer the stiffener is to the launching saddle the larger is the increase in both ductility and resistance.
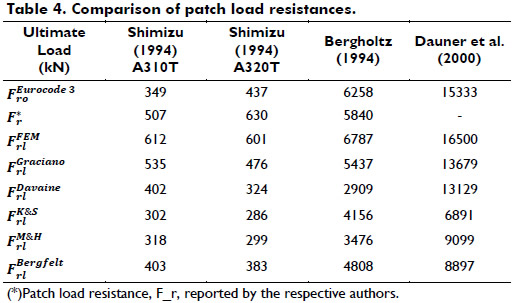
Table 4 summarizes the results obtained from the ultimate strength analysis conducted using some design models for longitudinally stiffened girder webs. Note that the ultimate loads obtained using the design procedure suggested in Eurocode 3 are consistently lower than both the nonlinear FEM predictions and the Fr reported by the original sources. In general, the equations proposed by Graciano (2002) give better predictions of the ultimate loads.
The influence of the longitudinal stiffeners is clear from the load-displacement responses presented in Figures 2, 4 and 6. Note that the load-deflection curves are the same at the beginning for both stiffened and unstiffened webs. For the stiffened girders, the general tendency of the nonlinear part of this curve reaches a higher load level, however after reaching the peak, it falls down and for larger deformations reaches the curve of the unstiffened girder.
Summary and conclusions
This paper presents a review of available formulae found in the technical literature for the estimation of the ultimate strength of steel bridge girders subjected to patch loading. The review included the provisions of the Europeans, American and Colombian design codes. Nonlinear FEM analyses of three case studies, involving actual launched bridges were performed in order to show the influence of the longitudinal stiffener and girder depth on the girders patch loadings resistance. Based on the aforementioned review and FEM analyses, the following conclusions can be drawn:
Longitudinal stiffeners increase the patch loading resistance and ductility of plate girder webs during incremental launching of bridge girders.
The idealized girder behavior in terms of load-displacement response can be appropriately studied by means of nonlinear FEM analyses.
The design procedure presented in Eurocode 3 considers the presence of a longitudinal stiffener; hence the results obtained in this way are satisfactory. However, the predicted patch loading capacities are consistently conservative for the case histories studied herein.
The design equations proposed by Graciano (2002) to calculate ultimate patch loading resistance of longitudinal stiffened plate girders produce better agreement with both experimental measurements and nonlinear FEM results.
The design codes AISC and NSR-10 must be reevaluated to include the beneficial effect of longitudinal stiffening on bridge girders subjected to concentrated loadings.
References
ABAQUS, Standard User's Manual, Version 6.11.1. (2011). (Vol. 1, 2 and 3). USA: Hibbitt, Karlsson & Sorensen. [ Links ]
American Institute of Steel Construction (AISC) (2010). Code of standard practice for steel buildings and bridges. Chicago, Illinois, USA. [ Links ]
Bergfelt, A. (1979). Patch loading on a slender web-influence of horizontal and vertical web stiffeners on the load carrying capacity. Chalmers University of Technology, Division of Steel and Timber structures Department of Structural Engineering. [ Links ]
Bergholtz, A. (1994). Lansering av brobalkar av stål -local intryckning över stöd. Chalmers University of Technology, Division of Steel and Timber structures Department of Structural Engineering. [ Links ]
BS 5400 Part 3 (2000). British Standard: Steel, concrete and composite bridges. Code of practice for design of steel bridges. [ Links ]
Carretero, A., & Lebet, J.-P. (1998). Introduction des forces concentrées dans les poutres élancées. Construction Métallique, (1), 5-18. [ Links ]
Cevik, A. (2007). A new formulation for longitudinally stiffened webs subjected to patch loading. Journal of Constructional Steel Research, 63, 1328-1340. [ Links ]
Clarin, M. (2007). Plate buckling resistance: Patch loading of longitudinally stiffened webs and local buckling. (Doctoral thesis). Lulea University of Technology, Sweden. [ Links ]
Chacón, R., Mirambell, E., & Real, E. (2013). Transversally stiffened plate girders subjected to patch loading. Part 1. Preliminary study. J. Constr. Steel Res., 80, 483-491. [ Links ]
Davaine, L. (2005). Formulations de la résistance au lancement d'une âme métallique de pont raide longitudinalement. (Doctoral thesis). INSA, Rennes, France. [ Links ]
Davaine, L., & Aribert, J.-M. (2005). Launching of steel girder bridge - Patch load resistance of longitudinally stiffened webs. In Proceedings of 4th European Conference on Steel and Composite Structures (pp. 143-149). Maastricht, The Netherlands. [ Links ]
Dauner, H.-G., Decorges, G., & Stucki, D. (2000). Web buckling strength for the launching of a box girder with a 130 m main span. Stahlbau, 69, 775-180. [ Links ]
Dubas, P., & Tschamper, H. (1990). Stabilité des âmes soumises à une charge concentrée et à une flexion globale. Const Met, 2, 25-39. [ Links ]
Eurocode 3 (2006). Design of Steel Structures. Part 1-5, General rules - Plated structural elements, BS EN 1993-1-5. British Standards Institution. [ Links ]
Eurocode 3 (2006). Design of Steel Structures. Part 2, Steel Bridges, BS EN 1993-2. British Standards Institution. [ Links ]
Galea, Y., Godart, B., Radouant, I., & Raoul, J. (1987). Test of buckling of panels subject to in-plane patch loading. In Proc. of the ECCS Colloquium on Stability of Plate and Shell Struct (pp. 65-71). Ghent University. [ Links ]
Graciano, C. (2001). Longitudinally stiffened steel plate girder webs under patch loading. Göteborg, Sweden: Chalmers Univ. of Tech., Department of Structural Engineering, Steel and Timber Structures. [ Links ]
Graciano, C. (2002). Patch loading: Resistance of longitudinally stiffened steel girder webs. (Doctoral thesis). Lulea University of Technology, Sweden. [ Links ]
Graciano, C., & Edlund, B. (2002). Nonlinear FE analysis of longitudinally stiffened girder webs under patch loading. J. Constr. Steel Res., 58, 1231-1245. [ Links ]
Graciano, C., & Johansson, B. (2003). Resistance of longitudinally stiffened I-girders subjected to concentrated loads. J. Constr. Steel Res., 59(5), 561-586. [ Links ]
Graciano, C., & Casanova, E. (2005). Ultimate strength of longitudinally stiffened I-girder webs subjected to combined patch loading and bending. J. Constr. Steel Res., 61, 93-111. [ Links ]
Graciano, C., Casanova, E., & Martínez, J. (2011). Imperfection sensitivity of plate girder webs subjected to patch loading. J. Constr. Steel Res., 67(7), 1128-1133. [ Links ]
Graciano, C., & Ayestarán, A. (2013). Steel plate girder webs under combined patch loading, bending and shear. J. Constr. Steel Res., 80, 202-212. [ Links ]
Graciano, C., Mendez, J., & Zapata-Medina, D. (2014). Influence of the boundary conditions on FE-modeling of longitudinally stiffened I-girders subjected to concentrated loads. Rev. Fac. Ing. Univ. Antioquia., 71, 221-229. [ Links ]
Granath, P. (1998). Serviceability limit state for plate girders during bridge launching. (Ph. D. thesis). Chalmers Univ. of Tech., Div. of Steel and Timber Structures, Göteborg, Sweden. [ Links ]
Janus, K., Karnikova, I., & Skaloud, M. (1988). Experimental investigation into the ultimate load behaviour of longitudinally stiffened steel webs under partial edge loading. Acta Technica CSAV, 2, 158-195. [ Links ]
Kutmanova, I., & Skaloud, M. (1992). Ultimate limit state of slender steel webs subjected to (i) constant and (ii) repeated partial edge loading. J. Constr. Steel Res, 21, 147-162. [ Links ]
Lagerqvist, O., & Johansson, B. (1996). Resistance of I-girders to concentrated loads. J. Constr. Steel Res., 39, 87-119. [ Links ]
Lagerqvist, O. (1995). Patch loading, resistance of steel girders subjected to concentrated forces. (PhD thesis), Lulea University of Technology, Div. of Steel Structures, Lulea, Sweden. [ Links ]
Lagerqvist, O. (1998). Resistance of bridge girder webs subjected to concentrated forces. J. Constr. Steel Res., 46, 62-64. [ Links ]
Markovic, N., & Hajdin, N. (1992). A contribution to the analysis of the behaviour of plate girders subjected to patch loading. J. Constr. Steel Res., 2, 163-173. [ Links ]
Navarro, M., Lebet, J.-P., & Beiloune, R. (2000). Launching of the Vaux Viaduct. Structural Engineering Int., 10, 16-18. [ Links ]
Asociación Colombiana de Ingeniería Sísmica (2010). NSR-10. Reglamento colombiano de construcción sismo resistente. [ Links ]
Pavlovcic, L., Detzel, A., Kuhlmann, U., & Beg, D. (2007). Shear resistance of longitudinally stiffened panels part 1: Test and numerical analysis of imperfections. J. Constr. Steel Res., 63, 337-50. [ Links ]
Seitz, M., & Kuhlmann, U. (2004). Longitudinally stiffened girder webs subjected to patch loading. In Proceedings of Steelbridge. [ Links ]
Seitz, M. (2005). Tragverhalten längsversteifter Blechträger unter quergerichteter Krafteinleitung. (Doctoral Thesis). Universität Stuttgart, Institute of Structural Design, Germany. [ Links ]
Shimizu, S. (1994). The collapse behaviour of web plates on the launching shoe. J. Constr. Steel Res., 31, 59-72. [ Links ]
Shimizu, S., Yoshida, S., & Okuhara, H. (1987). An experimental study on patch loaded web plates. Proc. of the ECCS Colloquium on Stability of Plate and Shell Structures (pp. 85-94). Ghent University. [ Links ]
Tryland, T., Hopperstad, O., & Langseth, M. (2001). Finite-element modeling of beams under concentrated loading. J. Struct. Eng., 127, 176-185. [ Links ]
Tschamper, H. (1991). Konzentrierte lasteinleitung und biegung an unversteiften schlanken Trägern. Stahlbau, 60, 5-14. [ Links ]
Walbridge, S., & Lebet, J.-P. (2001). Patch loading tests of bridge girders with longitudinal web stiffeners. Rapport d'essais, Ecole Polytechnique Federale de Laussane. [ Links ]
Zhang, Y., & Luo, R. (2012). Patch loading and improved measures of incremental launching of steel box girder. J. Constr. Steel Res., 68, 11-19. [ Links ]













