Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.35 no.1 Bogotá Jan.Apr. 2015
https://doi.org/10.15446/ing.investig.v35n1.44004
DOI: http://dx.doi.org/10.15446/ing.investig.v35n1.44004
M. Ramírez1 and R. Castellanos2
1Miguel Ramírez G. Electrical Engineer, National Polytechnic Institute (IPN), Mexico. M. Sc. in Electrical Engineer, La Laguna Institute of Technology, Mexico. Ph. D., University of Calgary, Canada. Affiliation: Mexican Electric Research Institute (IIE), T&D Department, Mexico. E-mail: miguel.ramirez@iie.org.mx
2Rafael Castellanos B. Electrical Engineer, Autonomous University of the State of Morelos (UAEM), Mexico. M. Sc. in Electrical Engineer, National Polytechnic Institute (IPN). Ph. D., CINVESTAV, Mexico. Affiliation: Mexican Electric Research Institute (IIE), T&D Department, Mexico. E-mail: rcb@iie.org.mx
How to cite: Ramírez, M., & Castellanos, R. (2015). Improvement of the dynamic behavior of large-scale power systems by using robust power system stabilizers based on fuzzy logic. Ingeniería e Investigación, 35(1), 65-70. DOI: http://dx.doi.org/10.15446/ing.investig.v35n1.44004
ABSTRACT
In this paper, the effect of fuzzy logic-based robust power system stabilizers on the improvement of the dynamics of a large-scale power system is investigated. The study is particularly focused on the Mexican Interconnected System and on adding damping to two critical inter-area system oscillation modes: the north-south mode and the western-peninsular mode. The fuzzy power system stabilizers (FPSSs) applied here are based on a significantly reduced rule base, small number of tuning parameters, and simple control algorithm and architecture, which makes their design and implementation easier and suitable for practical applications. Non-linear time-domain simulations for a set of test cases and results from Prony Analysis verify the robustness of the designed FPSSs, as compared to conventional PSSs.
Keywords: Large-scale power systems, inter-area oscillations, power system stabilizer, fuzzy logic.
RESUMEN
En el presente trabajo se investiga el efecto de estabilizadores de sistemas de potencia (PSSs) robustos, basados en lógica difusa, para mejorar la dinámica de sistemas de potencia complejos. En particular, el estudio se enfoca en mejorar el amortiguamiento de dos modos críticos de oscilación interárea del Sistema Interconectado Mexicano. Los PSSs difusos utilizados aquí se caracterizan por una base de reglas difusas reducida, pocos parámetros de sintonización y una arquitectura y algoritmo de control simples, lo cual facilita su diseño, implementación y aplicación práctica. Simulaciones en el dominio del tiempo con diversos escenarios de prueba y la aplicación del método de Prony comprueban la robustez de los PSSs difusos en comparación con PSSs convencionales.
Palabras clave: Sistemas de potencia complejos, oscilaciones interárea, estabilizador de sistemas de potencia, lógica difusa.
Received: June 13th 2014 Accepted: February 17th 2015
Introduction
Modern power systems are highly interconnected grids characterized by a very complex dynamic behavior. When subjected to a disturbance, complex modes of oscillation can be exhibited and become potentially unstable. Among the distinct types of oscillations usually recognized in the analysis and control of power system stability, inter-area modes of oscillation demand primary attention due to the number of machines participating from different areas and the severe effects they may have on system operation (Pal and Chaudhuri, 2005).
In general, a wide variety of methods have been developed in an attempt to resolve oscillatory stability problems in power systems. Among them, the Power System Stabilizer (PSS) is certainly one of the most effective, simple and economical methods commonly used by electric power utilities (Kundur, 1994). Typical PSS designs are based on a transfer function and a linear model of the system at some operating point, and power system damping is provided by appropriately tuning the phase and gain characteristics of the PSS compensation elements. This conventional PSS (CPSS) has been shown to contribute to the reduction of the unwanted effects of power system oscillations. However, the nonlinear characteristics, wide operating conditions and unpredictability of perturbations in power systems impose challenging problems to this linear controller (Hariri and Malik, 1999).
Unlike conventional control methods applied to the design of PSSs, artificial intelligence techniques, like fuzzy logic control, avoid the need for complicated mathematical models of the system dynamics by implementing the human expert control actions to different system scenarios through if-then rules. This alternative technique allows providing a robust and better solution to handle complex nonlinear systems and, therefore, is becoming a significant tool to effectively solve issues that are difficult to deal with conventional control strategies (Engelbrecht, 2007; Saxena et al., 2010).
In this paper, the application and effectiveness of robust fuzzy logic-based PSSs in enhancing the system damping of the Mexican Interconnected System (MIS) is investigated. As for this, two inter-area modes of oscillation are of particular interest: the one associated with interactions between the northern and southern regions, and the one that involves machines in the western area swinging against machines in the peninsular region. Non-linear time-domain simulations for a set of test cases and Prony Analysis are carried out to verify the performance of the fuzzy PSSs, as compared to conventional PSSs.
General description of the system
Structure
The MIS comprises an overall installed generating capacity of more than 51 GW, a main power transmission network of about 49,000 km among 400 kV, 230 kV and 161 kV lines, and a distribution system of approximately 693,000 km of lines. Electric power is generated by using various technologies and different energy sources and facilities.
The general structure of the MIS consists of seven interconnected areas designated as northwestern (NW), northern (N), northeastern (NE), western, (W), central (C), southeastern (SE) and peninsular (P). For the purpose of illustration, these areas can be arranged as shown in Figure 1.
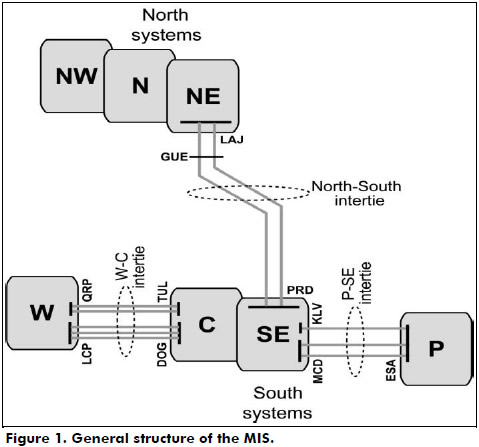
In an essentially longitudinal structure, long and sparse transmission paths characterize the MIS, and generation sources are usually situated far from the major consumption centers like Mexico City (in the C region), Monterrey (in the NE region) and Guadalajara (in the W region). The SE area of the MIS is the region with the largest generation capacity, where main hydroelectric generating stations, a large nuclear power plant and important thermal generation sources are located.
Considering that Mexico City and its metropolitan area take around 25% of the total system demand, and depending on generation schedules, seasonal energy characteristics, load levels and network topology, heavy power transfers from the southeastern to the central networks and from the north to the south systems can be required to meet the system load demand. However, power transfers across key interties of the system are currently limited to a great extent by dynamic stability constraints (Messina et al., 2003; Ramírez et al., 2012), since the loss of critical transmission lines and major generators can result in undamped inter-area oscillations.
Inter-area modes of oscillation
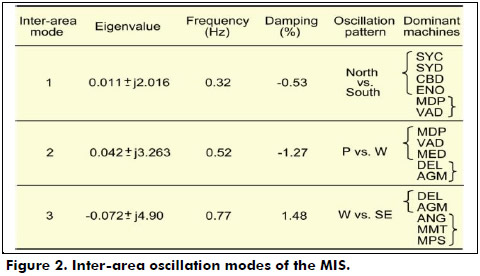
Earlier studies have shown that the MIS is characterized by three dominant and critical inter-area modes, involving the interaction of groups of machines spread over a large geographical area (Messina et al., 2003). Based on a dynamic model of the MIS for a 2004 test base case, with no PSSs in the system, the characteristics of these oscillation modes have been determined and are given in Figure 2 (Castellanos et al., 2007).
Considering the structure of the MIS in Figure 1, inter-area mode 1 is associated with the interaction of machines between the northern and southern regions; inter-area mode 2 involves mainly machines in the W area swinging against machines in the P region, and inter-area mode 3 denotes the interaction of machines in the W area oscillating against machines in the SE region. As noticed from the damping characteristics in Figure 2, the most critical modes of oscillation affecting the system dynamic behavior are inter-area modes 1 and 2. Therefore, the study is here focused on improving the stability of the MIS by working on these two inter-area oscillation modes and applying fuzzy PSSs.
Fuzzy PSS
The fuzzy PSS design used in the study is based on the simple fuzzy power systems stabilizer (SFPSS) derived in Ramirez and Malik, 2009. A brief summary of the formulation of the control algorithm is given next.
The controller output Vpss is determined by the following equation:

where Ko is the output scaling factor, su sets the sign of the control action, and uus is provided by the controller fuzzy inference mechanism according to the following four fuzzy rules:
R1: if d is ZO then uus is 0.00
R2: if d is SM then uus is 0.33
R3: if d is ME then uus is 0.66
R4: if d is BG then uus is 1.00
In the set of rules above, ZO, SM, ME, and BG stand for zero, small, medium and big, respectively, and are associated with triangular membership functions evenly distributed in the universe of discourse {0, 1}. As for d, it is a normalized variable determined in the following way:
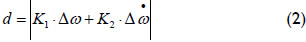
where K1 and K2 are the scaling factors for the generator speed deviation Δω and its derivative 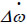 , respectively.
, respectively.
Finally,su in equation (1) is computed from the following expression:
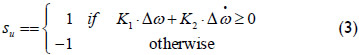
Advantages of the SFPSS are a significantly reduced rule base (only four fuzzy rules), small number of tuning parameters, and simple control algorithm and architecture. The simplicity of the SFPSS makes its design and implementation easier than other PSSs based on much more complex control algorithms (Ramirez and Malik, 2009).
System damping improvement trough SFPSSs
Earlier studies reported in specialized literature have identified the need to enhance the power system damping of the MIS, especially for severe operating conditions where major inter-area modes are excited. In this regard, different alternatives like the installation or retuning of conventional PSSs on main machines of the system, use of automatic load and generation shedding schemes, application of HVDC technology, and exploitation of supplementary controllers on installed FACTS devices have been suggested (Messina et al., 2003; Castellanos et al., 2007). At this point, the study is directed to the analysis and evaluation of the potential benefits of the previously described simple fuzzy PSS, when fitted on key machines of the MIS.
System model and simulation platform
The dynamic model of the MIS represents a realistic test system that accounts for the seven regional areas illustrated in Figure 1, and incorporates the representation of 2936 transmission lines, 1986 transformers, 419 generators (25 of them equipped with CPSSs), 3759 AC buses, 1638 loads, and 11 major SVCs. Base case load flow information for the system model is based on a 2004 peak load condition.
Simulation of the dynamic behavior of the system is carried out through the Transient Security Assessment Tool (TSAT) (TSAT, 2007), which is a commercial and non-linear time-domain simulation platform with extensive computational capabilities for complete assessment of power system dynamics.
SFPSS implementation
The previously described SFPSS was implemented in C programming language and then supplied to TSAT as a custom function block in the form of a Dynamic-Link Library module, which is incorporated into a User-Defined Model (UDM) as Dynamically Linked Block (DLB).
The SFPSS computer algorithm can be summarized into the following pseudocode:
IF sampling time instant THEN
OBTAIN speed deviation
COMPUTE speed deviation derivative
DETERMINE fuzzy inference system input
COMPUTE fuzzy inference system output
DETERMINE sign of the control action
COMPUTE control outputENDIF
In this work the control output is computed at every sampling interval, with a sampling rate of 25 Hz.
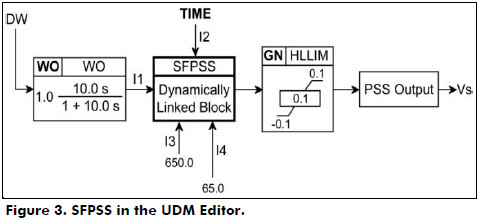
For illustration purposes the components of the model created in the UDM Editor are shown in Figure 3, where the block identified as WO carries out the washout function and the GN block is set for the scaling factor of the control output. Besides, the signal DW refers to the generator speed deviation, I1, I2, I3 and I4 identify the inputs to the DLB component, and Vs represents the SFPSS output.
Test scenarios
Extensive studies performed on the system (Messina et al., 2003; Castellanos et al., 2007) reveal that the loss of critical transmission lines has a considerable impact on the overall system response. For the present study and in order to illustrate the performance and robustness of the SFPSSs, and evaluate their effectiveness in enhancing the damping of inter-area oscillation modes of the MIS, the following contingencies were selected:
1. Step change of 1% in reference voltage of unit 1 at SYC power station.
2. Three phase to ground fault in one of the transmission lines of the LAJ-GUE 400 kV transmission path. The fault is cleared after 83.3 ms by the disconnection of the faulted circuit. The referred transmission path is part of the intertie linking the north and south regional areas of the MIS.
3. Three phase to ground fault at bus LAJ-400. The fault is cleared after 83.3 ms by the disconnection of circuit 1 of the LAJ-GUE 400 kV transmission path.
4. Three phase to ground fault at bus ESA-230, with a clearing time of 83.3 ms, and then trip of circuit 1 of the ESA-MCD 230 kV line that links the P and SE areas.
System operating conditions considered for the study include:
1. An 875 MW load flow from north to south through the North-South intertie, and a 109 MW power transfer from the P to the SE region.
2. Exchange of power as indicated in operating point 1, but with 875 MW and 280 MW across the north-south and P-SE interties, respectively.
3. Exchange of power as in operating point 1, but with 875 MW and 484 MW across the north-south and P-SE interties, respectively.
4. Exchange of power as indicated in operating point 1, but with 1000 MW and 109 MW through the north-south and P-SE paths, respectively.
Extensive studies in Castellanos et al., 2007, involving modal analysis and time domain simulations, identify the generating units at CBD and SYD power stations in the NE and N regions, respectively, and the machines at MDP power plant in the P region, as some of the major generators that could yield important improvements in the damping of inter-area oscillations through the application of supplementary stabilizing controls. Therefore, they were selected to be equipped with SFPSSs.
Selected test cases, with all contingencies applied at 0.1 s, and the corresponding results are presented next.
Simulation Results
System response under the application of the described test scenarios, and the installation of either SFPSSs or CPSSs on CBD, SYD and MDP power station generators is illustrated through the following test cases:
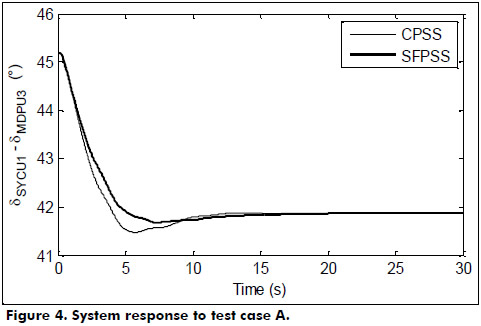
- Case A. Operating point 3, contingency 1, and PSSs installed on CBD units 1 to 4, SYD units 1 and 2, and MDP units 1 to 3. See Figure 4.
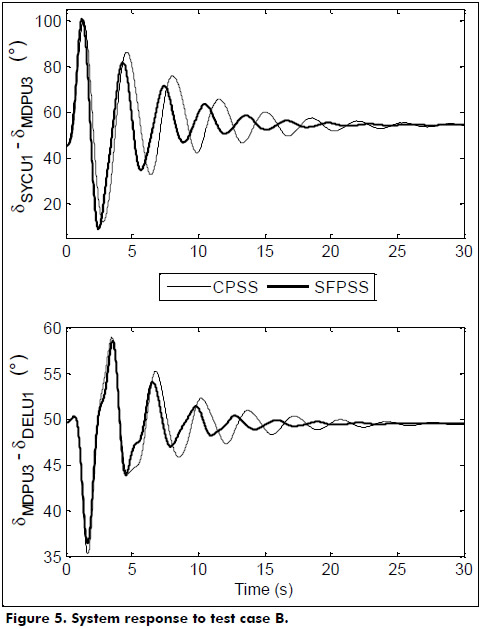
- Case B. Operating point 1, contingency 3, and PSSs installed on CBD units 1 to 4, SYD units 1 and 2, and MDP units 1 to 3. See Figure 5.
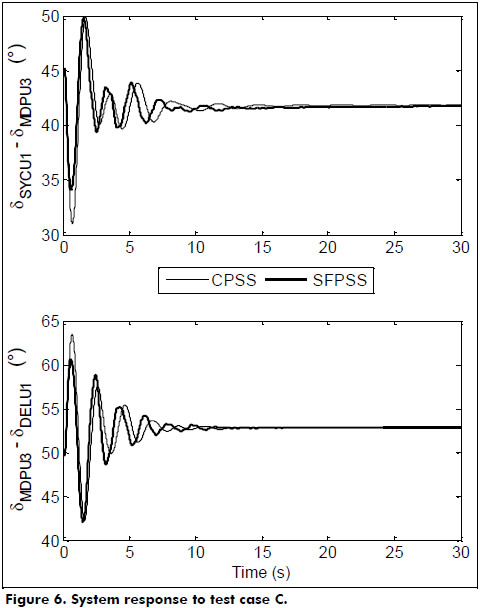
- Case C. Operating point 1, contingency 4, and PSSs installed as indicated in Case A. See Figure 6.
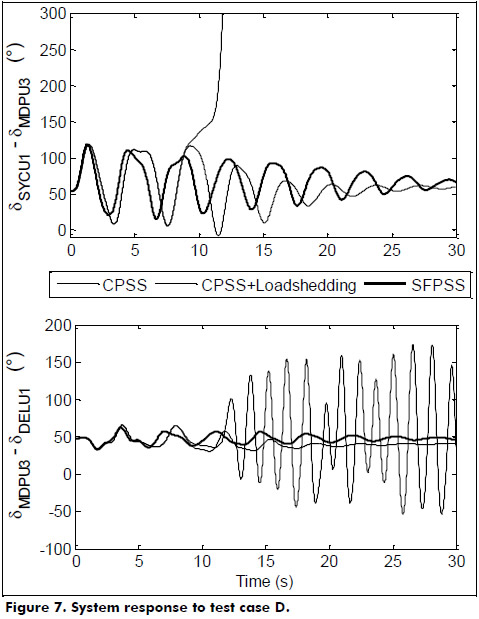
- Case D. Operating point 4, contingency 2, and PSSs installed as indicated in Case A. A 300 MW load shedding in the central region is also performed after 8 s for the case with CPSSs. See Figure 7.
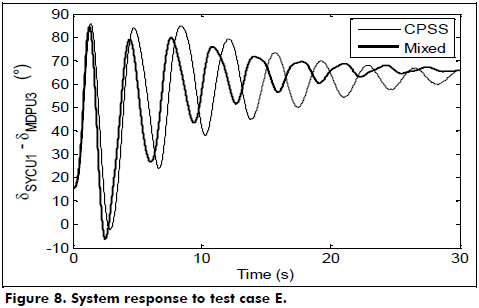
- Case E. Operating point 2, contingency 3, and CPSSs installed as indicated in Case A on one side. On the other side, SFPSSs are fitted on CBD units 1 to 4, SYD units 1 and 2, and MDP unit 3, and CPSSs on MDP units 1 and 2. See Figure 8.
Transfer function of the CPSSs installed on the indicated power station generating units is given in equation (4), where Tw is the time constant of the washout term, T1, T2, T3 and T4 are the time constants of the phase compensation components, and Kpss is the PSS gain.
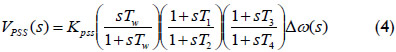
Parameters of the CPSSs used in the simulation studies were obtained from Castellanos et al., 2007.
Discussion
Simulation results in Figures 4 through 8 illustrates the power angle difference behavior related to the north-south and western-peninsular inter-area oscillation modes of the MIS, where the signals δSYCU1-δMDPU3 and δMDPU3-δDELU1 are respectively used for this purpose. From Figures 4 through 6 it can be noticed that, to a certain degree, the use of SFPSSs provides a better performance than the CPSSs in damping inter-area oscillation modes. However, an important benefit of the application of SFPSSs can clearly be seen from the results in Figure 7.
Figure 7 shows the system response for the test case D, where a power exchange of 1000 MW and 109 MW through the north-south and P-SE interties, respectively, is initially being accomplished. After the application of the contingency, growing oscillations start to emerge and, following a relatively short time, the sole use of CPSSs is not sufficient to maintain the system stability.
Regarding Figure 7 and by implementing a 300 MW load shedding in the central region of the MIS after 8 s, as a means to avoid the power system breakdown, the system can be made stable when the CPSSs are in operation. However, system response under the application of SFPSSs reveals that no load shedding action is required in this case since the SFPSSs are indeed capable of keeping the system stability. This implies that, as compared to CPSSs, fuzzy PSSs are more robust, and therefore SFPSSs can really increase the power transfer limits across the critical interties and avoid system power cuts with the great economical and also social consequences that avoidance of load shedding could bring.
Finally, system response in Figure 8 illustrates that both CPSSs and SFPSSs can cooperatively work and provide a better system damping effect than the sole use of CPSSs.
Some examples of how in this study the system damping ratio was improved with the application of SFPSSs are given in Figure 9. The information in this table was obtained from Prony Analysis (Ribeiro, 2009).

Conclusions
The effect of SFPSSs on damping two critical inter-area oscillations modes in a large scale and real test network, the Mexican Interconnected System, has been investigated in this study. A set of test cases were selected to compare the performance of the SFPSSs versus the CPSSs. Non-linear time domain simulations in a commercial platform and damping ratios estimated from Prony analysis illustrate the improved system damping performance that can be obtained by using SFPSSs. As compared to the CPSSs, the proposed SFPSSs showed better ability to keep the system stable after some critical perturbation.
The use of very simple fuzzy controllers, the SFPSSs, may avoid the application of load shedding measures, and the power cuts involved, to prevent the collapse of the power system. Besides, the simplicity of the SFPSS control algorithm makes it suitable for real-time and practical implementations.
The studies here performed reveal important evidence about the robustness and effectiveness of SFPSSs in improving the system dynamic behavior and encourage the realization of further investigations involving the wide scale utilization of SFPSSs in the Mexican Interconnected System.
References
Castellanos, R., Messina, A., Calderon, J. & Sarmiento, H. (2007, June). Large-scale use of FACTS technology for damping inter-area oscillations in the Mexican system. Paper presented at IEEE Power Engineering Society General Meeting, Tampa, USA. [ Links ]
Engelbrecht, A. P. (2007). Computational Intelligence. England: John Wiley and Sons Ltd. [ Links ]
Hariri, A. & Malik, O. P. (1999). Excitation control in power systems. In Wiley Encyclopedia of Electrical and Electronics Engineering (pp. 192-198). [ Links ]
Kundur, P. (1994). Power system stability and control. New York: McGraw-Hill. [ Links ]
Messina, A., Arroyo, J., Evaristo, N. & Castillo, I. (2003). Damping of low frequency inter-area oscillations using HVDC modulation and SVC compensator. Electric Power Components and Systems, 31 (4), 389-402. [ Links ]
Pal, B. & Chaudhuri, B. (2005). Robust control in power systems. New York: Springer Science+Business Media Inc. [ Links ]
Ramírez, J. M., Correa, R. E. & Hernández, D. C. (2012). A strategy to simultaneously tune power system stabilizers. International Journal of Electrical Power and Energy Systems, 43(1), 818-829. [ Links ]
Ramirez, M. & Malik, O. P. (2009, November). Simplified fuzzy logic controller and its application as a power system stabilizer. Paper presented at IEEE 15th International Conference on Intelligent System Applications to Power Systems, Curitiba, Brazil. [ Links ]
Saxena, D., Singh, S. N. & Verma, K. S. (2010). Application of computational intelligence in emerging power systems. Int. J. Eng., Sci. and Technol., 2(3), 1-7. [ Links ]
TSAT - Transient security assessment tool (2007). Version 7.0, Powertech Labs Inc. [ Links ]
Ribeiro, P. (2009). Time-varying waveform distortions in power systems. United Kingdom: John Wiley & Sons Ltd. [ Links ]













