Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.35 no.2 Bogotá May/Aug. 2015
https://doi.org/10.15446/ing.investig.v35n2.46318
DOI: http://dx.doi.org/10.15446/ing.investig.v35n2.46318.
A quantitative definition of engineering professional profiles
Definición cuantitativa de perfiles profesionales en ingeniería
M. C. Barrera1, O. G. Duarte2, C. Sarmiento3, and R. A. Soto4
1 Marla Constanza Barrera Botero. Systems Engineer, Universidad Distrital "Francisco José de Caldas", Bogotá. Master in Systems and Computer Engineering student, Universidad Nacional de Colombia, Colombia. E-mail: mcbarrerab@unal.edu.co.
2 Oscar Germán Duarte Velasco. Electrical Engineering, Universidad Nacional de Colombia, Colombia. Master in Industrial Automation, Universidad Nacional de Colombia, Colombia. Ph D. in informatics, Universidad de Granada, España. Affiliation: Associated professor, Universidad Nacional de Colombia, Colombia. E-mail: ogduartev@unal.edu.co
3 Carolina Sarmiento González. Systems Engineering, Universidad de San Buenaventura, Colombia. Master in Systems and Computer Engineering, Universi-dad Nacional de Colombia, Colombia. Affiliation: Ph D. in Systems and Computer Engineering student, Universidad Nacional de Colombia, Colombia. E-mail: csarmientog@unal.edu.co.
4 René Alexander Soto Pérez. Electrical Engineering, Universidad Nacional de Colombia, Colombia. Master in Industrial Automation, Universidad Nacional de Colombia, Colombia. Affiliation: Associated professor, Universidad Nacional de Colombia, Colombia. E-mail: rasotop@unal.edu.co.
How to cite: Barrera, M. C., Duarte, O. G., Sarmiento, C., & Soto, R. A. (2015). A quantitative definition of engineering professional profiles. Ingeniería e Investigation, 35(2), 89-95. DOI: http://dx.doi.org/10.15446/ing.investig.v35n2.46318.
ABSTRACT
A professional profile is a set of knowledge and skills. In this paper we propose a methodology to define professional profiles giving a quantitative assessment of skills and knowledge associated with an engineering curriculum. This approach can be used to evaluate the curriculum flexibility, i.e., if the curriculum offers the students diverse and flexible approaches and routes to learning. We describe a mathematical model that allows us to calculate the compliance level accomplished by a student with regard to one or more different profiles. Our proposal has been applied in the Undergraduate Program of Electrical Engineering from Universidad Nacional de Colombia.
Keywords: Profile, professional profile, individual profile, ideal profile, electrical engineering, curriculum, knowledge, skills, fuzzy implications, aggregation operators.
RESUMEN
Un perfil profesional es un conjunto de conocimientos y habilidades. En el presente artículo se propone una metodología para definir perfiles profesionales basada en una evaluación cualitativa de habilidades y conocimientos asociados con un plan de estudios de ingeniería. Esta metodología puede ser usada para evaluar la flexibilidad curricular, es decir, si el plan de estudios ofrece a los estudiantes enfoques y rutas de aprendizaje que sean diversos y flexibles. Aqui se describe un modelo matemático que permite calcular el grado de satisfacción logrado por un estudiante con respecto a uno o varios perfiles. Esta propuesta ha sido aplicada en el programa de pregrado de Ingeniería Eléctrica de la Universidad Nacional de Colombia.
Palabras clave: Perfil, perfil profesional, perfil ideal, perfil individual, ingeniería eléctrica, plan de estudios, conocimientos, habilidades, implicaciones difusas, operadores de agregación.
Received: October 17th 2014 Accepted: June 16th 2015
Introduction
A professional profile is a set of skills and knowledge that a professional (i.e. an engineer) has or should have. For engineering programs, it is difficult to define such professional profiles due to the inherent flexibility of those programs. Since we require flexibility in the curricula, the question is: how this flexibility affects the professional profile of the students?
There is no specific methodology to define professional profiles in educational institutions and organizations. Usually, professional profile definitions try to satisfy current needs and expectations from the academy, organizations and society. Educational institutions propose professional profiles according to what industry, organizations and society expect from new professionals.
The way that professional profiles are currently established involves common features (educational outcomes) that give us the basis to get to know the principal elements of a profile. These features can be classified in two major groups: skills and knowledge. In other words, a profile can be visualized as a set of skills and knowledge.
We have developed a methodology to evaluate professional profiles in the context of an engineering curriculum. We consider this methodology as a potential tool in educational institutions since it allows us to know if the curriculum fulfills the current expectations of the new professionals training.
In the section titled "Professional Profiles", the definition of professional profile is given and two important concepts derived from this are suggested.
Our proposed mathematical model is illustrated in the section titled "Mathematical Model". Our model was built using techniques taken from computational intelligence to propose a quantitative assessment of profiles. The effects of varying values of fuzzy implications and aggregator operators on the profiles are presented in the results.
Our methodology was applied at the Undergraduate Program of Electrical Engineering from Universidad Nacional de Colombia. A team of domain and human resources experts has helped us to build, test and evaluate the model. The application process is shown in the section titled "Application". Finally, we present conclusions and future work regarding this project.
Professional Profiles
Despite professional profiles arise from current needs from the academy, organizations and society, there is no specific methodology that defines or determines them. Even though each of these has their own definition of professional profiles, the techniques used by each one have common objectives: to satisfy the current and future needs from society and organizations; to develop personal and communication skills, besides the knowledge and skills within specific domain and to reinforce leadership and teamwork abilities (Crosthwaite , 2006; Horn , 2003; Alles, 2009). There is no formal definition of 'professional profile' that is universally accepted. However, the explicit definition is: "Previous image of features, knowledge, skills, values and feelings that should have been developed for a student in her/his training process" (Hernández, 2004).
According to the above definition, a professional profile is mainly based on the knowledge and skills expected by academy, society and organizations. For this reason, in our project we have defined that:
Definition 1. Professional profile: the set of skills and knowledge that a professional (i.e., an engineer) has or should have.
Individual and Ideal Profiles
We use the word 'or' in the previous definition in order to include two different concepts that have been adopted in this project: ideal profile, a professional profile expected; and individual profile, a professional profile acquired. Formally, we propose the following definitions:
Definition 2. Ideal profile: the set of skills and knowledge that a student must achieve according to his/her expected future professional role. These expectations are defined by educational institutions, industry, organizations and society, and they are based on current requirements of each sector.
Definition 3. Individual profile: the actual set of skills and knowledge acquired and/or developed by a student during the professional training process.
Definition 4. Compliance Level: itis the measure that determines to what extend an individual profile satisfies one or more ideal profiles. It is a quantitative assessment of skills and knowledge associated to a curriculum. The section "Mathematical Model" describes the model that we have developed to quantify this measure.
Knowledge Sources for Profile Obtaining
According with the first definition, a professional profile is composed by a set of skills and a set of knowledge. We need to relate each element from these sets with the curriculum, for this reason, three sources of knowledge have been the basis to build the sets of knowledge and skills and generate the frame to get both, individual and ideal profiles.
The three sources of knowledge are: 1. The Conceive, Design, Implement and Operate (CDIO) Syllabus, 2. Technical knowledge in Electrical Engineering, and 3. Electrical Engineering curriculum of Universidad Nacional de Colombia.
CDIO
CDIO is an initiative from the Massachusetts Institute of Technology (MIT) and other universities, whose goal is to integrate technical knowledge with some expected characteristics that a student should possess when he or she graduates from university. These features are based on needs from academy, industry and society. They allow engineers to work in real engineering teams to produce real products and systems (Crawley, 2001).
The CDIO initiative has created a new concept for undergraduate education based in the skills needed by the contemporary engineers and the appliance of an engineering problem solving paradigm. In this, two major tasks are involved: developing and codifying a comprehensive understanding of the skills needed by the contemporary engineer and developing new approaches to enable and enhance the learning of these skills.
A first outcome from this initiative was the CDIO Syllabus, a compendium of contemporary engineering knowledge, skills and attitudes that alumni, industry and academia desire in a future generation of young engineers. It consists of a template and an associate process, which can be used to capture the opinions of industry, alumni and faculty, and customize the Syllabus to a set of learning objectives appropriate for any specific undergraduate engineering program (Crawley, 2002).
The Department of Electrical and Electronic Engineering from Universidad Nacional de Colombia has adopted the CDIO methodology in their curricula since 2008, obtaining two outcomes:
- The CDIO Syllabus of the Electrical Engineering Curriculum (Departamento, 2008), a set of 704 skills organized in four levels as suggested in the CDIO methodology.
- The selection of 11 major learning objectives, each one associated to one or more evaluation criteria for engineering programs according to ABET (Accreditation Board of Engineering and Technology).
Curriculum
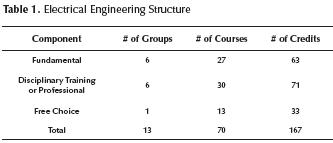
Resolution 181 of 2009 presents a complete structure of Electrical Engineering curriculum. In this structure, the curriculum is divided into three components, which are: Fundamental component, Disciplinary Training or Professional component and Free Choice component, each component is divided in groups and each group has one or several courses (Consejo, 2009).
A summary about structure of Electrical Engineering curriculum given in Resolution 181 of 2009 is presented in the Table 1.
Technical Knowledge
In the technical knowledge source was taking into account only the Disciplinary Training or Professional component, since this component contains the groups and courses that specify the training of the future Electrical Engineers.
In this context, the technical knowledge was acquired through consults in bibliographic sources and electrical engineering domain experts.
Representation of these three knowledge sources has been realized through ontologies, due that an ontology is a way to formally represent any kind of knowledge. (Sarmiento, 2010) describes the general structure in order to represent a curriculum through ontologies and (Soto, 2012, Ghisays, 2013) explain the representation of a part of technical knowledge where the courses were organized into thematic contents. These, in turn, divide each course by topics organized in different levels.
Mathematical Model
In the following sections, we describe our proposal of model in order to represent a professional profile and to calculate compliance levels. We use fuzzy implications and aggregation operators such as OWA, to find a level of compliance of an individual profile in regard to ideal profiles.
Profile Structure
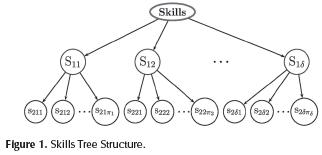
In the section "Professional Profiles", we have defined that a profile is composed of a set of skills and a set of knowledge. Since these skills and knowledge can be nested, they can be represented by a tree. The depth and number of node maybe different for each tree.
Definition 1. Let S a set of nested Skills.
S={s1,s2,s3...,sn}
S Is the set of all nodes of tree shown in Figure 1.
Definition 2. Let K a set of nested Knowledge.
K = {k1 k2, k3, ..., km}
The structure of set K is a tree and it is same at the structure of set S (see Figure 1).
According with profile definition and structure from skills and knowledge trees, we can represent a profile as a tree where the main nodes are skills and knowledge.
Definition 3. There is a function that assigns a numeric value to each element of the skills and knowledge trees called Competence Function.
μi (hi): S → [0,1]; σi (ci): K → [0,1]
Fuzzy Implications
In order to find the compliance level, it is necessary to establish a kind of relationship between an individual profile and an ideal profile.
Suppose that a value μi has been assigned to a skill in an ideal profile and a student e, i.e. an individual profile, has obtained a value  i in the same skill, the question is, how is it possible to determine the compliance level between the value obtained by the student and the value established in the ideal profile? For this, we propose to find this compliance level through fuzzy implications.
i in the same skill, the question is, how is it possible to determine the compliance level between the value obtained by the student and the value established in the ideal profile? For this, we propose to find this compliance level through fuzzy implications.
When applying fuzzy implications we can obtain the grade of membership of a set in regard to another set; in our case, the grade of membership of an individual profile with respect to an individual profile. We assimilate those grades as truth-values that are in the interval [0,1]. Relationships are represented through rules "if... then"; thus, truth values can be calculated with some T-norms or S-norms, as these kind of relationships can be represented in terms of ∧ or ∨, respectively (Driankov, et al., 1993).
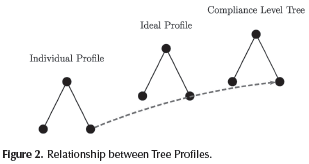
In this work, we use some fuzzy implications in order to find the values of the compliance level of a common node from both trees, individual and ideal profile. These trees must have the same structure (i.e. same number of nodes and depth). This process is made from leaf nodes to single root node, obtaining a new tree called Compliance Level Tree, as shown in Figure 2.
Aggregation Operators.
The aggregation problem consists in aggregating tuples of objects, all belonging to a given set, into a single object of the same set. An aggregation operator is a function, which assigns a single number y to any tuple of numbers (x1, x2,...xn, such that:
y= Aggreg (x1 x2..., xn)
Definition 4. An aggregation operator is a function,
Aggreg :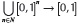
That satisfies:
• Identity: Aggreg(x) = x
• Boundary conditions: Aggreg(0,...,0) = 0 and Aggreg(1,...,1) = 1
• Monotonicity:
Aggreg (x1 x2.., xn )≤ Aggreg (y1 y2..., yn),
(x1 x2,... xn )≤ (y1,y2 ,...yn )
F (α1α2...,αn) = (1/n)Σin = 1 αi
(Detyniecki, 2001).
In our context, we use aggregation operators in the following cases:
In order to find a value to each parent node and root from skills and knowledge trees.
In order to assign a single numeric value to a skill or knowledge, each one has initially a value associated with each course from curriculum.
Through aggregation operators we can find a single numeric value that allows us to know the compliance level that a student has with respect to one or some ideal profiles. This value shows the compliance level of an individual profile regarding an ideal profile.
We have chosen a specific kind of aggregation operators called ordered weighted average (OWA) operators.
Definition 5. An OWA operator of dimensions n is a mapping F :  n→
n→  , such that:
, such that:
F (α1 α2,...αn)= 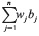
where b. is tmhe jth largest of the a, and the wi. are the weights, satisfying: w ∈ [1] and Σnj=1 = 1 (Yager, 2004, Merigó, 2011).
OWA operator provides a class of averaging operators parameterized by the weighting vector. This property gives us some of the basic aggregation operators such as:
-
Maximum. Where w1 = 0 and wj = 0 for j ≠ 1here F(a1 a2,...an) = Max.[a].
-
Minimum. Where wn = 0 and wj = 0 for j≠ n here F(av a2,...an) = Max.[a].
-
Simple Average. Where wn = 1/n here F(a1, a2,...an) = (1/n Σin=1 ai(Yager, 1988).
Additionally, it is possible define the weights values through various methods, too. Some of these methods imply:
-
Using learning algorithms with a set of training data, associating values and trying to assign the weights according to values from training data.
-
An exponential class of OWA operators. This is seen as a simple relationship between orness degree and a parameter that determines the OWA weights (Filev, , 1998).
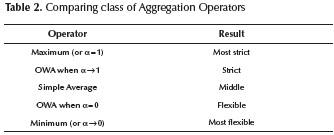
The orness degree determines how flexible (or strict) is the result on OWA operator and it is represented as α. When α → 1, OWA operator trends to maximum (or), and when α → 0 OWA operator trends to minimum (and).
Figure 3 shows the aggregation information process over the compliance level tree, which obtains the compliance level value from an individual profile with respect to an ideal profile.
Choosing Fuzzy Implications and Aggregation Operators
In the section "Fuzzy Implications", we were referring to the use of fuzzy implications in order to find the compliance level tree. The selection of a type of fuzzy implication determines the results expected for our model. There are different fuzzy implication operators reported (Driankov, 1993) and some of them are parameter adjustable. All of them extend the binary implication to fuzzy values: they compute the same values when the inputs are 0 or 1. However, their performance is different for values between 0 and 1. We analysed the performance of 9 fuzzy implication operators as compliance level operators, and selected Codel and Goguel implications.
Similarly, the choosing of an aggregation operator defines how flexible or strict the compliance level of an individual profile must be in regard to ideal profiles. In this case, we found the following results shown in the Table 2:
The next example aims to show the impact of α parameter on flexibility level in compliance level: suppose that there is a set of arguments values v (0.8, 0.5, 0,3) and a set of α (orness degree) values α= (0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, ), we have applied the exponential OWA in order to find the weights according with orness degree and establish the compliance level, the results obtained can be seen in Figure 4.
Application
In the section titled "Knowledge Sources for Profile Obtaining" we have described that three knowledge sources are the bases in order to build the general frame of individual and ideal profiles.
We have chosen two profiles defined by a group of experts by the Undergraduate Program of Electrical Engineering from Universidad Nacional de Colombia. These profiles are: Power distribution systems and Industry applications and they are the basis in order to obtain the ideal profiles.
We define an impact matrix (a table) for every professional profile. That matrix relates skills and knowledge with courses which was extracted from the Curriculum ontology (Sarmiento, 2010). In every cell of the matrix there is a numeric value in the interval [0,1] that reflects the expected impact that a course would have on a specific student's skill or knowledge. The values have been estimated by the same group of experts.
Notice, that every row of the matrix represents a skill or knowledge that belongs to the last level (a leaf node in the tree). In order to find the values of the higher levels where there are no designated values, we apply a kind of OWA operator that has been explained in "Aggregation Operators".
The impact matrices are the basis to create an individual profile. We use them in conjunction with the student's academic record to estimate the student's skills and knowledge acquired. In order to do this, we multiply the values of the impact matrices for a performance factor (and again in the interval [0,1]) that is proportional to the grade that the student obtained in every course.
It is possible design other kind of tests (for example, a test focused only in skills) and can use these. However, the design of these tests is not a part of this work. For this reason, we have used the academic record in order to find the individual profile.
Once we have established the relationship between skills or knowledge and the level of performance of a student, we need to assign a single value for each skill or knowledge. For this reason, we propose to use OWA operators in each row from each matrix.
Ideal profiles have also been obtained from a group of experts. They have provided us two profile matrices that link skills and knowledge sets with the two ideal profiles, where each cell contains numeric value in the interval [0,1].
In order to find the compliance level of an individual profile with respect to ideal profiles, we apply fuzzy implications to get the compliance level tree described in "Fuzzy Implications". This gives us the level of compliance obtained by a student in each one of the skills and knowledge.
With OWA operators it is possible to calculate the compliance level of an individual profile in regard to one or more ideal profiles as an only numeric value in the interval [0,1], as it has been described in "Aggregation Operators".
In order to test and evaluate the proposed methodology, a software prototype has been implemented. The main purpose of this software prototype is to facilitate the evaluation of the model by experts in the domain of knowledge in Electrical Engineering, i.e., teachers, Electrical Engineers and human resources experts.
Using the web application, a user can select a student, one, several or all ideal profiles, fuzzy implications and OWA operators (and an α parameter if it is required). The user can see the compliance level value and the compliance level tree (see Figure 5).
We have used the Rational Unified Process (RUP) methodology of software design. This prototype is a Web application that has been implemented in PHP language and it is based on a MySQL database. The database has nine tables with information about the sets of skills and knowledge, students, courses of curriculum and ideal profiles related with the Undergraduate Program of Electrical Engineering from Universidad Nacional de Colombia. In addition to this, the database records the information regarding compliance levels of individual profiles.
Example
The goal of this example is to show the application of our model in order to find the compliance level of a student or individual profile regarding an ideal profile.
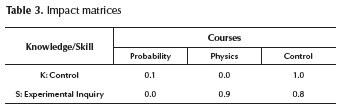
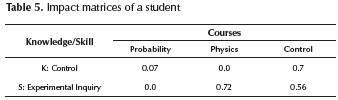
Suppose that we have an impact matrix that relates the knowledge Control and the skill Experimental Inquiry with 3 courses Probability, Physics and Control Table 3 shows the values given to this relationship.
A student e has obtained the next grades, these have been normalized and they can be seen in the Table 4.
In order to find the individual profile, we propose to associate impact matrices and student grades, obtaining the results shown in the Table 5.
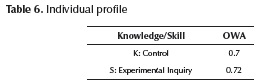
We need a unique numeric value by each knowledge and skill, in this case, we propose to use a kind of aggregation operator (for example, maximum). These results allow us to build the individual profile that can be seen in Table 6.
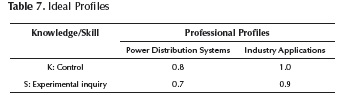
Suppose that we have ideal profiles defined by academic experts related with the knowledge Control and Skill Experimental inquiry. Table 7 shows the structure established to each ideal profile:
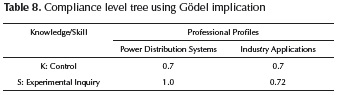
Through Fuzzy Implications it is possible to establish a relationship between individual and ideal profiles in order to build the compliance level tree. The application of Codel implication is shown in Table 8.
Finally, we need know the compliance level of a student respect to the Ideal profiles. In order to obtain this result we propose to apply an OWA operator over the compliance level tree of Table 8. In the Table 9 we show the results when an OWA operator is applied, in this case we find an exponential OWA with an orness degree value 0.8. This outcomes show that the student e has a compliance level in the profile Power distribution system greater than the profile Industry Applications.
Conclusion and Future Work
A methodology to define professional profiles (ideal and individual) has been proposed. The mathematical foundations of the methodology have been presented. It is a quantitative model based on skills and knowledge. Two main tools taken from the Knowledge Engineering are used: fuzzy implications and aggregation operators. As those tools are not unique, it is possible to conduct some sensitivity analysis. As an example, we have tested: 1) the influence of the selection of the fuzzy implication operation, and 2) the effect of the orness parameter in the aggregation process.
As further work, more experimentation is needed in order to adjust the methodology. Analysis of real cases is required. A close work with the domain experts must be done in order to define the skills and knowledge trees and the impact matrix. The potential of the methodology is broad: for example, it can be used in program assessment tasks since it is possible to measure if the expectations from organizations and society are being fulfilled. From another perspective, it can be used for students as an information tool about their individual learning processes.
Currently, our methodology is the basis of a project whose goal is to recommend learning pathways for students in the Electrical Engineering curriculum from Universidad Nacional de Colombia. As the optimal pathway depends on the desire professional profile, this quantitative model is the keystone of the project.
References
Alles, M. (2009). Diccionario de competencias, La trilogía: Las 60 competencias más usadas, Buenos Aires, Argentina: Editorial Garnica. [ Links ]
Consejo de Facultad de Ingeniería. (2009). Resolución 181 de 2009, Universidad Nacional de Colombia, sede Bogotá [ Links ].
Crawley, E. F. (2001). Creating the CDIO Syllabus a Statement of Coals for Undergraduate Engineering Education, Department of Aeronautics and Astronautics, Massachusetts Institute of Technology. [ Links ]
Crawley, E. F. (2002). The CDIO Syllabus a universal template for Engineering Education, ASEE/IEEE Frontiers in Education Conference. [ Links ]
Crosthwaite, C., Cameron, I., Lant, P. and Litster, J. (2006). Balancing curriculum processes and content in a project centred curriculum. in pursuit of graduate attributes, Icheme (Institution of Chemical Engineers), 84(7), 619-628. DOI: 10.1205/ece.05002. [ Links ]
Davies, J., Fensel, D. and van Harmelen, F. (2003). Towards the Semantic Web. Ontology-Driven Knowledge Management, New York, USA: Jhon Willey and Sons. [ Links ]
Departamento de Ingeniería Eléctrica y Electrónica, Universidad Nacional de Colombia. (2008). CDIO Syllabus en español, documento de aplicación de la metodología CDIO al departamento de Ingeniería Eléctrica y Electrónica, Universidad Nacional de Colombia, sede Bogotá [ Links ].
Detyniecki M. (2001). Fundamentals on Aggregation Operators., Computer Science division, University of California. [ Links ]
Driankov, D., Hellendoorn, H. and Reinfrank, M. (1993). An Introduction to Fuzzy Control, Berlin, Germany: Springer-Verlag. DOI: 10.1007/978-3-662-11131-4. [ Links ]
Fensel, D., Holger, L., Polleres, A., de Brujin, J., Stollberg, M., Roman, D. and Domingue, J. (2007). Enabling Semantic Web Services. The Web Service Modeling Ontology, Berlin, Germany: Springer-Verlag. DOI: 10.1007/978-3-540-34520-6. [ Links ]
Filev, D., and Yager, R. (1998). On the issue of obtaining OWA operator weights, Fuzzy Sets and Systems, 157-169. DOI: 10.1016/S0165-0114(96)00254-0. [ Links ]
Ghisays, A. (2013). Representación del Programa Curricular de Pregrado de Ingeniería Eléctrica de la Universidad Nacional en el Área de Circuitos, Señales y Sistemas mediante Ontologías, Bogotá, Colombia: Facultad de Ingeniería, Universidad Nacional de Colombia. [ Links ]
Hernández Díaz, A. (2004). Perfil Profesional, Revista Pedagógica Universitaria, 9(2), 69-98. [ Links ]
Horn, E. and Kupries, M. (2003). A study program for professional software engineering, Proceedings of the 16th Conference on Software Engineering Education and Training (CSEET'03). DOI: 10.1109/csee.2003.1191389. [ Links ]
Merigó, J.M. (2011). A unified model between the weighted average and the induced OWA operator, Expert Systemswith Applications, 38(9), 11560-1157. DOI: 10.1016/j.eswa.2011.03.034. [ Links ]
Merigó, J.M. and Casanovas, M. (2011). The uncertain induced quasi-arithmetic OWA operator. International Journal of Intelligent Systems, 26(1), 1-24. DOI: 10.1002/int.20444. [ Links ]
Sarmiento, C. (2010). Representación del Programa Curricular de Pregrado de Ingeniería Eléctrica de la Universidad Nacional, mediante Ontologías, Bogotá, Colombia: Facultad de Ingeniería, Universidad Nacional de Colombia. [ Links ]
Soto, R. (2012). Representación del área de Electrotecnia y Sistemas de Potencia del programa curricular de Ingeniería Eléctrica, mediante Ontologías, Bogotá, Colombia: Facultad de Ingeniería, Universidad Nacional de Colombia. [ Links ]
Yager, R. (1988). On ordered weighted averaging aggregation operators in multicriteria decision making. IEEE Transactions on Systems, Man and Cybernetics, 18(1), 183-190. DOI: 10.1109/21.87068. [ Links ]
Yager, R. (2004). OWA aggregation over a continuous interval argument with applications to decision making, IEEE Transactions on Systems, Man and Cybernetics, 34(2), 1952-1963. DOI: 10.1109/TSMCB.2004.831154. [ Links ]