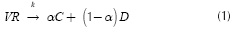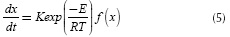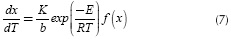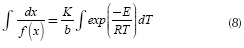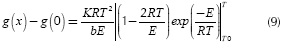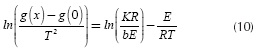Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.35 no.3 Bogotá Sept./Dec. 2015
https://doi.org/10.15446/ing.investig.v35n3.49498
DOI: http://dx.doi.org/10.15446/ing.investig.v35n3.49498.
Kinetic analysis of the thermal decomposition of Colombian vacuum residua by thermogravimetry
Análisis cinético de la descomposición térmica de fondos de vacío colombianos mediante termogravimetría
F.A. Díaz1, A. Chaves2, M.P. Maradei3, D. Fuentes4, A. Guzmán5, and H. Picón6
1 Fabian Andrey Diaz. Affiliation: Doctorate student. Universidad Industrial de Santander, Bucaramanga, Colombia.
Email: fabiandiazmateus@hotmail.com.
2 Arlex Chaves. Affiliation: Ph,D and Professor. Universidad Industrial de Santander, Bucaramanga, Colombia.
Email: achavesg@uis.edu.co.
3 Maria Paola Maradei. Affiliation: Ph,D and Professor. Universidad Industrial de Santander, Bucaramanga, Colombia.
Email: mapaomar@uis.edu.co.
4 David Fuentes. Affiliation: Ph,D and Professor. Universidad Industrial de Santander, Bucaramanga, Colombia.
Email: dfuentes@uis.edu.co.
5 Alexander Guzmán. Affiliation: Ph,D and Researcher. Ecopetrol S.A. - Instituto Colombiano del Petróleo, Bucaramanga, Colombia.
Email: alexander.guzman@ecopetrol.com.co.
6 Héctor Picón. Affiliation: MSc and Researcher. Ecopetrol S.A. - Instituto Colombiano del Petróleo, Bucaramanga, Colombia.
Email: hector.picon@ecopetrol.com.co.
How to cite: Díaz, F.A., Chaves, A., Maradei, M.P., Fuentes, D., Guzmán, A., & Picón, H. (2015). Kinetic analysis of the thermal decomposition of Colombian vacuum residua by thermogravimetry. Ingeniería e Investigación, 35(3), 19-26. DOI: http://dx.doi.org/10.15446/ing.investig.v35n3.49498.
ABSTRACT
Five different Colombian vacuum residues were thermally decomposed in a thermogravimetric analyzer. Three heating rates were employed to heat the sample up to 650 °C. The kinetic analysis was performed by the Coats-Redfern method to describe the non-isothermal pyrolysis of the residua. A reaction model where the reaction order gradually increases from first to second order is proposed, resulting on an excellent agreement of the experimental with the calculated data. The results also indicate that the pyrolysis of a vacuum residue cannot be modeled by a single reaction mechanism.
Keywords: TGA, pyrolysis, distillables, coke, coking, asphaltenes.
RESUMEN
Cinco fondos de vacío colombianos fueron procesados mediante descomposición térmica en una balanza termogravimétrica. Tres tasas de calentamiento fueron empleadas para calentar la muestra hasta una temperatura de 650 °C. El análisis cinético fue realizado mediante el método de Coats-Redfern para describir la pirólisis no isotérmica del residuo, se propuso un modelo de reacción donde el orden de la reacción aumenta gradualmente de primer a segundo orden y se encontró un excelente ajuste de los datos calculados con los datos experimentales. Los resultados también indican que la pirólisis de un fondo de vacío no puede ser modelada por un solo mecanismo de reacción.
Palabras clave: Balanza termogravimétrica, termogravimetría, pirólisis, destilables, coque, asfaltenos, coquización.
Received: March 5th 2015 Accepted: July 29th 2015
Introduction
The bottom product of a vacuum distillation unit is known as vacuum residua. It is an extremely heavy hydrocarbon with API gravity under 12 and it is sometimes solid at room temperature. Vacuum residues usually have a high concentration of nickel, vanadium and sulfur and they are the preferred feed for high conversion processes such as delayed coking and flexi-coking. Due to the increase of heavy oil production around the world, the vacuum residua production has also increased and refiners have been searching for ways to make it more profitable. In this way, the conversion of vacuum residua has gained interest in recent years.
Thermogravimetry is a widely used calorimetric technique where a sample is heated at a certain heating rate and its weight is constantly measured. In the case of hydrocarbons, as the temperature rises the sample decomposes into lighter hydrocarbons and coke, which remains in the sample container. This technique is widely used for kinetic analysis, since the experiments are easily and quickly performed. In addition, the kinetic parameters are not so different from those obtained in a batch reactor (Almerri 2004). The maximum heating rate found in the literature is 150 °C/min (Yue & Watkinson 1997) and the maximum temperature is around 800 °C. A carrier inert gas has to be used to remove the products of the thermal decomposition. The most commonly used carrier gases are nitrogen and argon at flow rates of 10 - 150 ml/min.
Several studies on the thermal decomposition of vacuum residua by thermogravimetry are available in the literature. For example, Schucker (1983) presented a study on the thermal decomposition of heavy Arab vacuum residua and its fractions, where the heating rates range from 1 °C/min to 20 °C/min, the carrier gas was helium at 38ml/min, the maximum temperature was 600 °C, and the weight of the samples was about 20mg. The resulting data was analyzed by the Friedman method (Friedman 1965) to obtain kinetic parameters, and the activation energies were found to increase with conversion. The most commonly used methods for kinetic analysis of thermogravimetric data will be explained further ahead. Posteriorly, Yue & Watkinson (1997) analyzed synthetic crude pitch at heating rates from 25 °C/min to 150 °C/min up to 800 °C. The weight of the sample was around 15mg. They analyzed the data using four different methods and found that the integral 2-step method with a first order reaction model presented the best agreement with the experimental data.
Similarly, Park & Kim (2006) performed a thermogravimetric analysis of one vacuum residua at heating rates between 2 °C/min - 20 °C/min up to 800 °C. Nitrogen flowed at a flow rate of 300 ml/min. They found the integral 2-step method with a first order reaction model to provide the best adjustment to the experimental data. Guo, Zhang & Wang (2008) processed five Chinese petroleum residues and four fractions of one of them. They claim to use Sharp's differential method but in Sharp & Wentworth (1969) it can be seen that Sharp's differential method is equivalent to the Coats-Redfern method (Coats & Redfern 1964). These researchers used a heating rate of 5 °C/min up to 680 °C. The carrier gas was nitrogen at a flow rate of 50ml/min. The agreement of the experimental data with the kinetic method was not presented, though they make an analysis of the interaction of the fractions of the vacuum residue and its effect in the coke yield; they also presented a linear relationship of the coke yield to the Conradson carbon residue (CCR).
Trejo, Rana & Ancheyta (2010) processed the fractions of a Mexican residue at heating rates from 4 °C/min to 16 °C/min up to 900 °C. The carrier gas was nitrogen at a flow rate of 50ml/min. They used the Friedman method to describe the kinetics of the thermal decomposition and good agreement is presented with the experimental data. Wang et al. (2012) presented a thermogravimetric analysis of the fractions of a Venezuelan vacuum residue and a Chinese vacuum residue. The heating rate was 15 °C/min, the maximum temperature was 550 °C, the carrier gas was nitrogen at rate of 100 ml/min and the sample weight was about 4mg. These researchers did not present a kinetic analysis but rather focused on the interactions of the fractions and how this affected the coke yield.
Finally, Guo et al. (2013) presented a thermokinetic analysis for four vacuum residua: Daqing, Karamay, Liaohe and Venezuela. The weight of the sample was 10 - 15 mg, the carrier gas was nitrogen at 100 ml/min and the heating rates were 10, 15 and 20 °C/min. These authors performed a kinetic analysis with the Sharp and the Friedman methods and assured that the Friedman method with a 1.5 order reaction model presented the best agreement with the experimental data. They also claimed that the Sharp method could be used to determine kinetic parameters if the proper reaction model was selected.
It can be concluded, from the revision of the literature, that the method selected for the kinetic analysis of thermogravimetric data is simply the one that provides the best agreement with the experimental data. However, it must be noted that the integral and the Coats-Redfern method provide a single set of kinetic parameters, while the Friedman method provides different sets of kinetic parameters as a function of the conversion ratio. Since the object of this work is to obtain a kinetic model that represents appropriately the non-isothermal pyrolysis of a vacuum residua and its thermal decomposition into distillables and coke -which will be used in a numerical simulation of the delayed coking process- a single set of kinetic parameters is desirable. For this reason, the Coats-Redfern method was chosen for this study.
The pyrolysis of vacuum residua has been described as a decomposition into distillables and coke by several researchers, employing a first order reaction model (Del Bianco et al. 1993, Sawarkar et al. 2007) and a second order reaction model (Martinez, Benito & Callejas 1997, Wang & Anthony 2003). For this reason, the experiments in the thermogravimetric analyzer were expected to provide appropriate kinetic parameters to describe the decomposition of vacuum residua.
In the delayed coking process the feed is subjected to a high thermal disruption in the coking furnace. According to Schobert (2013), the feed is heated from 200 °C to about 500 °C in less than three minutes, which gives a heating rate of about 100 °C/min. The thermogravimetric analyzer employed in this research provides a maximum heating rate of 90 °C/min and, in order to provide a complete set of kinetic parameters, heating rates of 60 °C/min and 30 °C/ min were also employed in the experiments.
Methods for kinetic analysis of thermogravimetric data
The most common methods for kinetic analysis of thermogravimetric data are: the integral method, the Coats-Redfern method, the Friedman method and the Chen-Nuttall method (Chen & Nuttall 1979). A complete revision of these methods can be found in Yue & Watkinson (1997). The Friedman method has the disadvantage that kinetic parameters K and E are functions of the conversion. As result, a set of parameters is found according to the number of divisions made on the entire range of conversion. For instance, Almerri (2004) took intervals of 0.05 between 0.1 - 0.9. Trejo, Rana & Ancheyta (2010) and Schucker (1983) took intervals of 0.1 between 0 - 1. On the other hand, the most employed method is the Coats-Redfern, which is basically the same as the integral method with a small modification that will be explained further on in this paper. With this method a single set of K and E parameters are found and there is a wide set of reaction models that can be used in order to find the best agreement with the experimental data. The Coats-Redfern method is presented as follows.
The thermal decomposition (pyrolysis) of vacuum residua (VK) into distillables (D) and coke (C) can be written as:
The extent of the reaction can be described by the product of a function of temperature and a function of conversion:
The integration of Equation (2) gives:
The term x corresponds to the conversion which is calculated with:
Where , mg, mF and mF are initial, final and mass at any time t. The term k(t) is replaced with the Arrhenius kinetic Equation:Nevertheless, in a non-isothermal thermogravimetric experiment the temperature (T) at any time t can be represented as a linear function of t:
Taking the derivative of Equation (6) and replacing it in Equation (5), it is possible to eliminate de dependence on time, obtaining:
Separating variables and integrating:
The integral term on the right hand of Equation (8) does not have an exact solution. Coats & Redfern (1964) proposed to replace it with its order one Taylor expansion, so it leads to the following expression:
Since the values of E lie in the range 100 - 300 kJ/mol, the term. This is the difference with the integral method, where this term is not neglected. With this assumption, Equation (9) leads to:
If plotting ln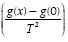 versus
versus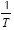 traces a straight line, the slope provides the value of E and the intercept the value of K. The function g(x) is replaced with the reaction model that provides the best fit in the linear regression. Some reaction mechanisms are presented in Table 1.
traces a straight line, the slope provides the value of E and the intercept the value of K. The function g(x) is replaced with the reaction model that provides the best fit in the linear regression. Some reaction mechanisms are presented in Table 1.
For a wider set of reaction mechanisms see Cedeno, Ramirez & Garea (1992); Capart, Khezami & Burnham (2004) and Ebrahimi-Kahrizsangi & Abbasi (2008).
Experimental procedure
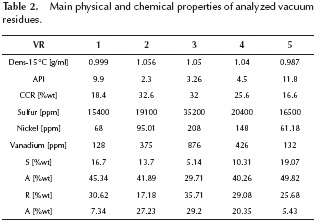
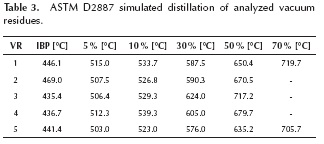
Five vacuum residues from Barrancabermeja Refinery (Barrancabermeja, Colombia) were heated up to 650 °C at rates of 30 °C/min, 60 °C/min and 90 °C/min. The carrier gas was nitrogen at a flow rate of 150 ml/min. A purge gas of nitrogen flowed downwards at a rate of 140 ml/min. The weight of the sample was around 100 mg. The equipment employed was a Thermo Cahn THERMAX 300. In order to eliminate the errors produced by buoyancy, blanks were made for each heating rate. Vacuum residues 2, 3 and 4 were solid at room temperature while residues 1 and 5 were extremely viscous fluids. Densities, Conradson carbon residue (CCR), sulfur, nickel and vanadium concentrations and SARA fractions of the vacuum residues can be seen on Table 2. ASTM D2887 simulated distillations can be seen on Table 3, where the high values of the IBP (Initial Boiling Point) show that vaporization is not expected in the experiments, only pyrolysis reactions.
Results and discussion
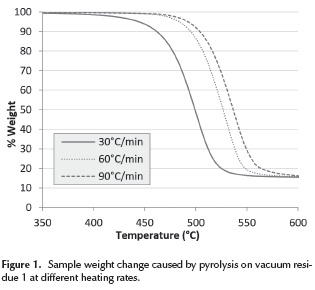
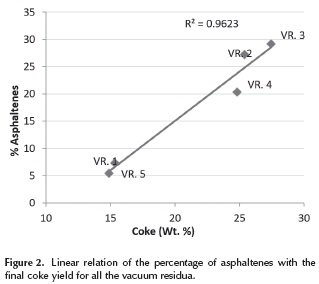
The results of the experiments in the thermogravimetric analyzer (TGA) on vacuum residue 1 are presented in Figure 1. Here, it can be seen how the weight of the sample decreases as a result of the pyrolysis reactions that form distillables and coke. The distillables are evacuated with the carrier gas and the coke remains in the container. A displacement of the curves with increasing heating rate can also be seen. It occurs because, when the heating rate is high, the sample temperature lags behind that of the furnace due to a delay in the heat transfer from the furnace to the sample. Vacuum residua 2, 3, 4 and 5 exhibited similar curves. The final yield of coke in all vacuum residues can be correlated with a linear regression to the weight percentage of asphaltenes as seen on Figure 2. This direct proportionality is expected, given that asphaltenes have been considered by many authors as the main precursors of coke (Wiehe 1993, Speight 1998).
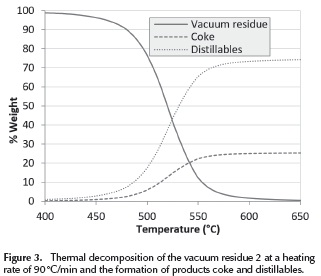
Thermal decomposition of the vacuum residue 2 at a heating rate of 90 °C/min and the formation of products coke and distillables(D) and coke (C) are presented in Figure 3. The formation of coke is calculated as (x * mf ), the decomposition of vacuum residua is calculated as (mt - mCoke) and the formation of distillables is calculated as (m0 - mt). It can be seen that at 650 ºC the vacuum residue is fully converted into distillables and coke. It can also be seen that most of the conversion occurs between 500 and 550 ºC.
Kinetic analysis by linear regression
Yue & Watkinson (1997) and Park & Kim (2006) performed a two-step analysis with the Coats-Redfern method employing the first order reaction model. In their investigation, the plotting of 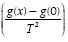 versus
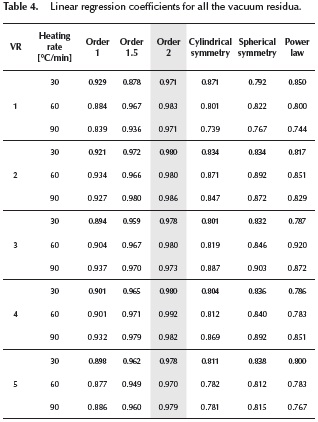
versus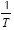 traces two nearly perfect straight-lines. These researchers described the two straight lines as a two steps reaction model. The experimental data presented in this work did not present such behavior. Several reaction mechanisms were evaluated, those that provided the best linear regression coefficient (closer to 1.0) are presented on Table 4. The reaction model that provided the best linear regression coefficient of the experimental data obtained for vacuum residua 1, 2, 3, 4 and 5 is the second order reaction model. The complete set of activation energies and frequency factors is presented on Table 5, the %Error is calculated with Equation (11).
traces two nearly perfect straight-lines. These researchers described the two straight lines as a two steps reaction model. The experimental data presented in this work did not present such behavior. Several reaction mechanisms were evaluated, those that provided the best linear regression coefficient (closer to 1.0) are presented on Table 4. The reaction model that provided the best linear regression coefficient of the experimental data obtained for vacuum residua 1, 2, 3, 4 and 5 is the second order reaction model. The complete set of activation energies and frequency factors is presented on Table 5, the %Error is calculated with Equation (11).
Kinetic analysis by least squares
The regression coefficients presented on Table 5 are not satisfactory, and the values of the %Error show poor agreement of the experimental data with the calculated values. The kinetic parameters obtained by linear regression can be optimized by a non-linear least squares optimization. Values obtained by linear regression were used as a starting point in the optimizations, since several local optimums were found. A complete description of the non-linear least squares method can be found in Marquardt (1963). In this method, an objective function, also called residual sum of squares, is minimized. This function is calculated as follows:
As the agreement of the calculated values with the experimental data with the second order reaction model are not satisfactory, a first order and a 1.5 order reaction model were also analyzed. The Equations for these models are shown on Table 6.
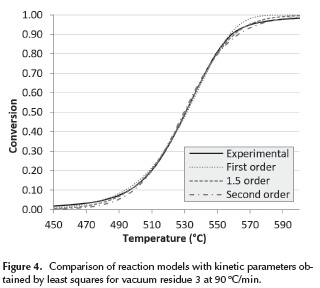
The performance of the first order, 1.5 order and second order reaction models is analyzed in Figure 4. Here, it can be seen how at lower temperatures the experimental data looks like a first order reaction; but as temperature increases, it looks like a 1.5 order, and at the end of the reaction it looks like a second order reaction. A similar behavior can be identified in all the analyzed vacuum residua at every heating rate.
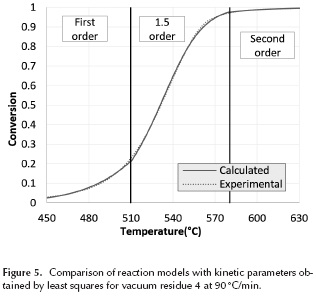
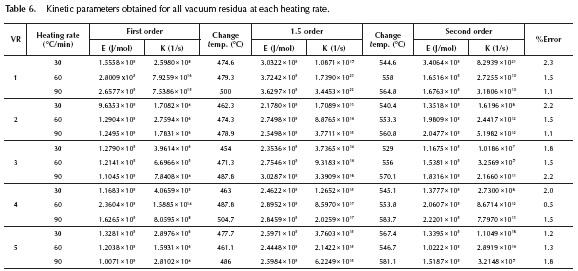
This change in the reaction mechanism in the thermal processing of vacuum residua has also been reported by Guo et al. (2013). At lower temperatures the thermal cracking reactions dominate the system and mild thermal cracking such as the one that occurs in visbreaking has been described by many researchers as a first order reaction (Del Bianco et al. 1993, Sawarkar et al. 2007) where mainly saturates and alkyl radicals are involved. At higher temperatures the condensation reactions -which involve mostly heavy complex molecules- dominate the system, since most saturates and aromatics have already been decomposed. Several researchers have described the thermal decomposition of the remaining fractions of resins and asphaltenes as a second order mechanism (Martinez, Benito & Callejas 1997, Wang & Anthony 2003). Based on this observation, a reaction model where the reaction mechanism increases from first to second order is proposed. The reaction mechanism was changed at the point where it produces the lowest %Error with the experimental data. The results for vacuum residue 4 can be seen in Figure 5 and the complete set of kinetic parameters for all vacuum residua can be seen on Table 6. The reaction model proposed in this work provides an excellent agreement of the calculated with the experimental data.
Conclusions
An investigation on the pyrolysis of five Colombian vacuum residues in a thermogravimetric analyzer was performed. The kinetic parameters obtained by linear regression of the Coats-Redfern method with a second order reaction model show a poor agreement of the calculated with the experimental data, even though it provided the best linear regression coefficients. Given these results it can be concluded that the thermal decomposition of a vacuum residue cannot be simulated by a single reaction mechanism. Other researchers have studied the thermal decomposition of vacuum residua and, in order to improve the agreement of the calculated with the experimental data, have presented a two-step model with a first order reaction mechanism. The experimental data studied in this work did not present such behavior.
A first order, 1.5 order and a second order reaction mechanisms were analyzed and, when compared with the experimental data, it was observed that the reaction mechanism gradually changes from first to second order. It occurs because at lower temperatures the thermal cracking reactions dominate the reaction system; but as temperature rises the condensation reactions increase as well, and in the end they control the reaction rate.
The kinetic parameters obtained by least squares optimization where the reaction mechanism changes from first to 1.5 and from 1.5 to second order show an excellent agreement of the experimental with the calculated data. The errors obtained are between 0.5 - 2.3 %, which is very low, since the error inherent to the TGA equipment is between 0 - 1 %. The non-isothermal decomposition of vacuum residua is correctly represented by this changing reaction mechanism reaction model. The full extent of the reaction is correctly represented as a decomposition of the residua into distillables and coke.
Nomenclature
Subscripts
References
Almerri, H. A. (2004). Correlation and modeling of thermal cracking yields in the delayed coking process. Ph. D. thesis dissertation, The University of Tulsa, Tulsa, USA. [ Links ]
Capart, R., Khezami, L. & Burnham, A. K. (2004). Assessment of Various Kinetic Models for the Pyrolysis of a Microgranular Cellulose. Thermochimica Acta, 417(1), 79 - 89. DOI: 10.1016/j.tca.2004.01.029. [ Links ]
Cedeño, L. C., Ramírez, J. S. & Garea, B. M. (1992) Estudio cinético del tratamiento térmico de materiales lignocelulósicos. Tecnol, Ciencia Ed. (IMIQ), 8(2), 26 - 31. [ Links ]
Chen, K., Liu, H., Guo, A., Ge, D. & Wang, Z. (2012). Study of the Thermal Performance and Interaction of Petroleum Residue Fractions during the Coking Process. Energy & Fuels, 26(10), 6343 - 6351. DOI: 10.1021/ef301378g. [ Links ]
Chen, K., Wang, Z., Liu, H., Ruan, Y. & Guo, A. (2013). Thermodynamic and thermokinetic study on pyrolysis process of heavy oils, J. Therm. Anal. Calorim. 112(3), 1423 - 1431. DOI: 10.1007/s10973-012-2652-4. [ Links ]
Chen, W. J. & Nuttall, H. E. (1979). A TGA study of Colorado oil shale with a new kinetic model, 86th AIChE National meeting, Houston, Texas. DOI: 10.1038/201068a0. [ Links ]
Coats, A. W. & Redfern, J. P. (1964) Kinetic Parameters from Thermogravimetric Data, Nature, 201, 68 - 69. [ Links ]
Del Bianco, A., Panariti, N., Anelli, M., Beltrame, P. L. & Carniti, P. (1993). Thermal cracking of petroleum residues. 1. Kinetic analysis of the reaction. Fuel, 72(1), 75 - 80. DOI: 10.1016/0016-2361(93)90380-k. [ Links ]
Ebrahimi-Kahrizsangi, R. & Abbasi, M. H. (2008). Evaluation of reliability of Coats-Redfern method for kinetic analysis of non-isothermal TGA. Trans. Nonferrous Met. Soc. China, 18(1), 217 - 221. DOI: 10.1016/S1003-6326(08)60039-4. [ Links ]
Friedman, H. L. (1965). Kinetics of thermal degradation of char-forming plastics from thermogravimetry. Application to a phenolic plastic. Journal of Polymer Science: Part C(6), 183-195. [ Links ]
Guo, A., Zhang, X. & Wang, Z. (2008). Simulated delayed coking characteristics of petroleum residues and fractions by thermogravimetry. Fuel Processing Technology, 89(7), 643 - 650. DOI: 10.1016/j.fuproc.2007.12.006. [ Links ]
Marquardt, D. W. (1963). An algorithm for least squares estimation of non-linear parameters. J. Soc. Indust. Appl. Math., 11(2), 431 - 441. DOI: 10.1137/0111030. [ Links ]
Martinez, M. T., Benito, A. M. & Callejas, M. A. (1997). Thermal cracking of coal residues: kinetics of asphaltene decomposition. Fuel, 6(9), 871 - 877. DOI: 10.1016/S0016-2361(97)00048-3. [ Links ]
Park, H. Y. & Kim, T. H. (2006) Non-isothermal pyrolysis of vacuum residue (VR) in a thermogravimetric analyzer. Energy Conversion and Management, 47 (15), 2118 - 2127. DOI: 10.1016/j.enconman.2005.12.009. [ Links ]
Sawarkar, A. N., Pandit A. B. & Joshi, J. B. (2007). Studies in Coking of Arabian Mix Vacuum Residue. Chem. Eng. Res. Des., 85 (4), 481 - 491. DOI: 10.1205/cherd06159. [ Links ]
Schobert, H. (2013). Chemistry of fossil fuels and biofuels. Cambridge University Press, New York, USA. DOI: 10.1017/cbo9780511844188. [ Links ]
Schucker, R. C. (1983). Thermogravimetric determination of the coking kinetics of Arab heavy vacuum residuum. Ind. Eng. Chem. Process Des. Dev., 22(4), 615 - 619. DOI: 10.1021/i200023a011. [ Links ]
Sharp, J. M. & Wentworth, S. A. (1969). Kinetic analysis of thermogravimetric data. Analytical chemistry, 41(14), 2060 - 2062.DOI: 10.1021/ac50159a046. [ Links ]
Speight, J. G. (1998). The chemistry and physics of coking, Korean J. Chem. Eng., 15(1), 1 - 8. DOI: 10.1007/BF02705298. [ Links ]
Trejo, F., Rana, M. S. & Ancheyta, J. (2010). Thermogravimetric determination of coke from asphaltenes, resins and sediments and coking kinetics of heavy crude asphaltenes. Catalysis Today, 150(3), 272 - 278. DOI: 10.1016/j.cattod.2009.07.091. [ Links ]
Wang, J. & Anthony, E. J. (2003). A study of thermal-cracking behavior of asphaltenes. Chem. Eng. Sci, 58(1), 157 - 162. DOI: 10.1016/S0009-2509(02)00430-X. [ Links ]
Wiehe, I. (1993). A Phase separation kinetic model for coke formation, Ind. Eng. Chem. Res., 32 (11), 2447 - 2454. DOI: 10.1021/ie00023a001. [ Links ]
Yue, C. & Watkinson, A. P. (1997). Pyrolysis of pitch. Fuel, 77(7), 695 - 711. DOI: 10.1016/S0016-2361(97)00236-6. [ Links ]