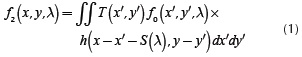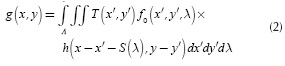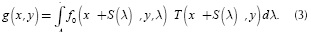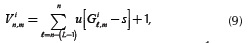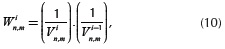Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.35 no.3 Bogotá Sept./Dec. 2015
https://doi.org/10.15446/ing.investig.v35n3.49868
DOI: http://dx.doi.org/10.15446/ing.investig.v35n3.49868.
High-dynamic range compressive spectral imaging by grayscale coded aperture adaptive filtering
Reconstrucción de imágenes espectrales compresivas con alto rango dinámico por medio de filtrado adaptativo en escala de grises
N. Diaz1, H. Rueda2, and H. Arguello3
1 Nelson E. Diaz Diaz: BSc. in Computer Sciences and Master Student in Computer Sciences at Universidad Industrial de Santander, Colombia. Affiliation: Master Student at Universidad Industrial de Santander, Colombia.
E-mail: nelson.diaz@correo.uis.edu.co.
2 Hoover Rueda: BSc in Computer Sciences and MSc at Universidad Industrial de Santander, Colombia. Ph.D student at University of Delaware, Newark DE, USA. Affiliation: Ph.D student at University of Delaware, Newark DE, USA.
E-mail: rueda@udel.edu.
3 Henry Arguello: F. BSc in Electrical engineer and MSc in Electrical power at Universidad Industrial de Santander, Colombia. Ph.D in Electrical and Computer engineering from the University of Delaware, USA. Affiliation: Associated professor at Universidad Industrial de Santander, Colombia.
E-mail: henarfu@uis.edu.co.
How to cite: Diaz, N., Rueda, H., & Arguello, H. (2015). High-dynamic range compressive spectral imaging by grayscale coded aperture adaptive filtering. Ingeniería e Investigación, 35(3), 53-60. DOI: http://dx.doi.org/10.15446/ing.investig.v35n3.49868.
ABSTRACT
The coded aperture snapshot spectral imaging system (CASSI) is an imaging architecture which senses the three dimensional information of a scene with two dimensional (2D) focal plane array (FPA) coded projection measurements. A reconstruction algorithm takes advantage of the compressive measurements sparsity to recover the underlying 3D data cube. Traditionally, CASSI uses block-unblock coded apertures (BCA) to spatially modulate the light. In CASSI the quality of the reconstructed images depends on the design of these coded apertures and the FPA dynamic range. This work presents a new CASSI architecture based on grayscaled coded apertures (GCA) which reduce the FPA saturation and increase the dynamic range of the reconstructed images. The set of GCA is calculated in a real-time adaptive manner exploiting the information from the FPA compressive measurements. Extensive simulations show the attained improvement in the quality of the reconstructed images when GCA are employed. In addition, a comparison between traditional coded apertures and GCA is realized with respect to noise tolerance.
Keywords:Compressive sensing, hyperspectral imaging, saturation, dynamic range, coded aperture, optical imaging.
RESUMEN
El sistema de adquisición de imágenes espectrales basado en una apertura codificada de única captura (CASSI) es una arquitectura para muestrear imágenes espectrales que captura información de una escena en tres dimensiones mediante medidas proyectadas y codificadas del sensor en dos dimensiones (2D). Para recuperar el cubo de datos se emplea un algoritmo de reconstrucción que aprovecha la esparcidad de las medidas compresivas. Tradicionalmente, CASSI usa aperturas codificadas binarias para modular espacialmente la luz. En CASSI la calidad de las imágenes reconstruidas depende del diseño de estas aperturas codificadas y de la saturación del sensor. Este trabajo presenta una nueva arquitectura CASSI basada en aperturas codificadas de escala de grises (ACG), la cual reduce la saturación en el sensor e incrementa el rango dinámico de las imágenes reconstruidas. El conjunto de ACG se calcula en tiempo real de forma adaptativa explotando la información contenida en las medidas compresivas del sensor. La mejora obtenida en la calidad de las imágenes reconstruidas se muestra a partir de diversas simulaciones en las que se utilizan las ACG. Adicionalmente, se lleva a cabo una comparación entre las aperturas codificadas tradicionales y las ACG con respecto a la tolerancia del ruido.
Palabras clave: Muestreo compresivo, imágenes hiperespectrales, saturación, rango dinámico, apertura codificada, imágenes ópticas.
Received: March 27th 2015 Accepted: July 29th 2015
Introduction
The coded aperture snapshot spectral imaging system (CASSI) is an imaging architecture which senses the three dimensional information of a scene with a single two dimensional (2D) coded random projection measurement set (Wagadarikar, et al. 2008). The CASSI optical architecture comprises five optical elements: an objective lens is used to form an image of a scene in the plane of the coded aperture; a coded aperture modulates the spatial information over the complete wavelength range; a relay lens transmits the coded light field onto a dispersive element that disperses the light before it impinges on the focal plane array (FPA). Given a set of compressive measurements, compressive sensing theory (CS) (Candes 2006, Donoho 2006, Baraniuk 2007) is used to reconstruct the underlying data cube of size N x N x L from just N(N + L - 1) measurements, where n is the spatial dimension and l is the spectral depth of the data cube. In CASSI, the quality of the reconstructed images relies on the design of the set of 2D coded apertures, whose entries block or transmit the light from the scene. These coded apertures are called block-unblock coded apertures (BCA).
A single shot in CASSI may not provide sufficient number of compressive measurements. A recent modification in CASSI allows multi-shot sensing procedures which increase the number of compressive measurements, (Arguello and Arce 2013, Arguello and Arce 2014, Rueda and Arguello 2013, Rueda, et al, 2014). In this modification, each shot uses a distinct coded aperture that remains fixed during the integration time of the detector. The quality of the reconstructed images improves in CASSI in proportion to the number of compressive measurements (Arguello and Arce, 2011). Each CASSI shot adds simultaneously N(N+l-1) compressive measurements. Therefore, the total number of available measurements with k shots is KN(N + L- 1).
The FPA's dynamic range is the ratio between the smallest and the largest value detected by the sensor. The largest value is known as saturation level. Saturation occurs when compressive measurements exceed the saturation level, i.e., the quantizer's dynamic range. In that case, the measurements take the value of the saturation level (Laska, et al, 2011). In CASSI and multi-shot CASSI, each saturated pixel in the sensor induces errors in the reconstructed image. Typically, CASSI system employs CCD or CMOS sensor, both affected by saturation depending on their dynamic range.
In order to avoid saturation the coded apertures can be used to modulate the incoming light in the system. Traditionally, BCA are implemented using piezo systems (Kittle, et al, 2010) or a digital-micromirror-device (DMD) (Wu, et al, 2011), to vary the coding pattern in each snapshot. The disadvantage of BCA is that their entries can take just two binary values {0,1}; that is, the modulation of the intensity to binary entries. In order to improve intensity modulation, we propose the use of grayscale-adaptive coded apertures (GCA) which can be also implemented using a DMD. The new design takes advantage of the fast switching time of the micro-mirrors which enables the use of a pulse-width modulation technique for the production of grayscale values. GCA can be used to yield a modulation of the intensity and to increase the dynamic range of the reconstructions.
This work extends the compressive capabilities of CASSI by replacing the traditional BCA by a set of GCA. GCA-CASSI multi-shot is motivated by the possibility of reducing saturation levels through modulation of the amplitude of the incoming scene.
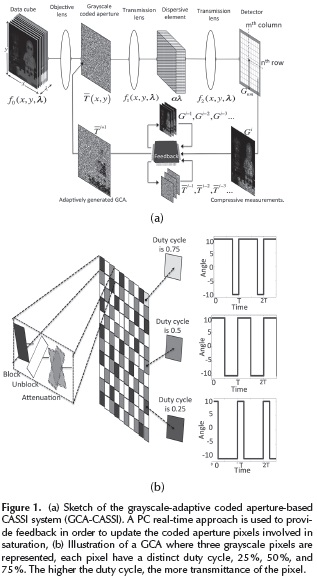
Figure 1a shows the sketch of the proposed architecture. The adaptive process is accomplished through a PC realtime model (Feedback), in which the PC receives the measurement Gi from the FPA and remembers the previous compressive measurements Gi+1, G1+2, Gi+3 and the previous coded aperture patterns. Using the adaptive filter (AF), the micro-mirrors are updated in the DMD, and the AF attenuates the coded aperture between snapshots, yielding an adaptively generated GCA 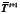 . Figure 1b shows the detail of the grayscale-adaptive coded aperture where the attenuated pixel represents an oscillating DMD. In Figure 1b the pixels from the DMD are selected with 25 %, 50 %, and 75 % of duty cycle; the higher the duty cycle, the greater transmittance of the pixel. In the following sections we introduce the block-unblock CASSI optical model and present the grayscale-adaptive-based model. Simulations are performed to evaluate the improvements attained by the proposed grayscale-adaptive coded apertures.
. Figure 1b shows the detail of the grayscale-adaptive coded aperture where the attenuated pixel represents an oscillating DMD. In Figure 1b the pixels from the DMD are selected with 25 %, 50 %, and 75 % of duty cycle; the higher the duty cycle, the greater transmittance of the pixel. In the following sections we introduce the block-unblock CASSI optical model and present the grayscale-adaptive-based model. Simulations are performed to evaluate the improvements attained by the proposed grayscale-adaptive coded apertures.
System model
The CASSI system uses a traditional block-unblock coded aperture (BCA) T(x,y) to modulate the spatio-spectral density f0(x, y, λ), where (x,y) are the spatial dimensions and λ represents the spectral dimension. The resulting coded field is then dispersed by the dispersive element, resulting in,
where T (x',y') is the transmission function representing the coded aperture, h(x-x'-S(λ), y-y') is the optical impulse response of the system and S (λ) is the dispersion induced by the prism. The compressive measurements across the FPA are obtained by the integration of the field f2(x,y, λ)over the detector range sensitivity. Therefore, the spectral density in front of the detector is given by g (x, y) = ∫ƒ2 (x, y, λ) dλ. When the signal measurement is replaced in g (x,y) the resulting equation is:
When the optical impulse response of the system is assumed linear and ideal, the spectral density being integrated is given by:
Representing the detector as a spatially pixelated array with pixel size Δd, the measurements in the presence of noise ω, at the (n,m)th position can be represented as:
where m, n represent the (m, n)th pixel in the FPA sensor, and rect(.) is the rectangular function. Similarly, the coded aperture T(x, y) can be represented as a spatially pixelated array. Assuming the coded aperture pixel size as Δt and T'n,'m represents a binary value, (0) block and (1) unblock, the coded aperture can be expressed as,
The coded aperture in Equation (5) can be replaced in Equation (4). Thus, the detector measurement becomes
Representing the spatio-spectral source density being integrated on the detector in discrete form as Fn,m,k such that n∈{1,...,N} indexes the x -axis, m∈{1,...,N} the y -axis, and k∈{1,...,L} the wavelength, Equation (6) can be succinctly expressed as
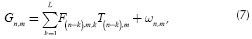
where Gn,m is the intensity at the (m,n)th position of the detector with dimensions N(N+L- 1), the spectral data cube Fhas size N x N x L, Tn,m is the (m,n)th value in the coded aperture and ω represents the noise of the system.
Grayscale CASSI system model
In this paper the BCA is replaced with a GCA, which modulates the source along the spatial coordinates. The CASSI system architecture with GCA (GCA-CASSI) is illustrated in Figure 1a, where the traditional BCA is replaced by the GCA depicted in Figure 1b. The coding is now performed by the GCA represented by 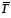 (x,y) which is applied to the spatio-spectral density source f0(x,y, λ), resulting in the coded field f1(x,y,λ). This coded field differs from the one achieved with the BC, given that a particular element of the GCA attenuates the wavelengths instead of blocking or unblocking the complete spectrum at a given spatial location. The entries of the GCA
(x,y) which is applied to the spatio-spectral density source f0(x,y, λ), resulting in the coded field f1(x,y,λ). This coded field differs from the one achieved with the BC, given that a particular element of the GCA attenuates the wavelengths instead of blocking or unblocking the complete spectrum at a given spatial location. The entries of the GCA 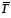 n,m, . vary in the range {0 (l-1)}, being l the number of grayscale levels of the DMD. In this way, Equation (7) can be rewritten as,
n,m, . vary in the range {0 (l-1)}, being l the number of grayscale levels of the DMD. In this way, Equation (7) can be rewritten as,
FPA saturation in CASSI
Saturation occurs when the measurements exceed the dynamic range of the sensor quantizer. The quantizer has finite dynamic range due to two reasons: the first is related to physical limitations that allow a finite range voltage to be correctly converted to bits; and the second is that only a finite number of bits are available to represent each value. Quantization with saturation is referred to as finite-range quantization (Laska, et al, 2011). The errors imposed by finite-range quantization are unbounded. CS recovery techniques only provide guarantees for noise that is bounded, or bounded with high probability (Laska, et al, 2011). Dealing with saturation is important in CASSI because it reduces the attainable reconstruction quality. Figure 2 shows examples of compressive measurements, generated using Equation (7), three distinct percentages of saturated pixels (0 %, 5 % and 10 %, respectively), and their corresponding attained reconstructions using 4 shots. Notice that the higher the saturation percentage, the lower the quality of the reconstructed image.
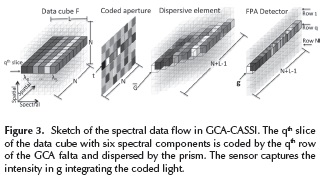
In order to understand how the saturation in CASSI occurs, the qth slice of the data cube in Figure 3 is analyzed. It shows a representation of the physical phenomenon in CASSI, where t is the coded aperture of the qth row, 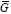 is the qth the coded and dispersed slice, and g is the FPA measurement of the qth slice.
is the qth the coded and dispersed slice, and g is the FPA measurement of the qth slice.
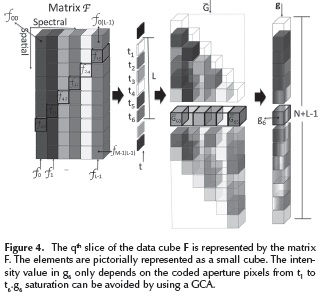
Figure 4 shows a top-view of the integration process of the FPA sensor. The pixel g6 is analyzed in order to understand the saturation in the sensor's pixels. The qth slice of the data cube F is represented by the matrix F. Each ƒn,m element is pictorially represented as a small cube.
The 6th compressive measurement in the qth row is given by 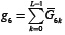 , where each
, where each 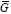 6k is integrated in the sensor and is given by
6k is integrated in the sensor and is given by 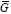 6k = t6-kƒ6-k,k , k = 0,...,Ll. The intensity value in g6 only depends on the coded aperture pixels from t1 to t6. The saturation at g6 can be avoided by replacing the BCA by a GCA.
6k = t6-kƒ6-k,k , k = 0,...,Ll. The intensity value in g6 only depends on the coded aperture pixels from t1 to t6. The saturation at g6 can be avoided by replacing the BCA by a GCA.
Adaptive estimation of the GCA
In order to reduce the saturation level from the compressive measurements, an adaptive filter (AF) is designed to adaptively penalize the entries of the coded apertures, so the input source is attenuated before it is integrated by the detector. Consequently, these coded apertures will exhibit non-binary values, thus generating GCA. Formally, let Vi represent a weight matrix whose entries are a measure of how many times the ith coded aperture pixel affects a saturated pixel in the sensor. In particular, the entries of Vi can be written as
where u[.] is the unit step function. Gilm is the (l,m)th pixel from the ith compressive measurement. i ∈ {1 ,K} and K is the number of total snapshots. The number of shots can be expressed in terms of compressive ratio. The latter can be defined as Cr = (k(N(N + L 1)))/N2L, where K represents the number of shots, and N and L the spatial and spectral dimensions. Cr can be seen as the ratio between the reconstructed measurements and the number of pixels in the reconstructed data cube; s = 2b1 represents the saturation level of the sensor, which depends on the number of bits "b" of the sensor. Notice that Equation (9) can be easily calculated in a PC real time approach (Feedback). Based on the weight matrix, a penalization function is generated by assuming that the attenuation in a pixel of the coded aperture is inversely proportional to the number of saturated pixels in the FPA. That is, the penalization function can be seen as the attenuation matrix wi whose entries Win,m are given by,
where V0 is assumed to be an one-value matrix. Notice that the attenuation matrix W takes into account the previous weighted matrices as in a memory AF approach. Given the K randomly generated coded apertures T1,...,TK, the GCA 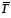 ...,
...,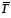 k are generated according to,
k are generated according to,
where AoB is the Hadamard product between the matrices A and B. Notice that 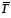 1 = T1, that is, the first GCA remains as the original, since the AF needs feedback. After the second snapshot some measurements still remain saturated. The effect of the AF improves the quality of reconstructed images when the remaining saturated measurements are discarded. The measurements that continue to be saturated in each snapshot are discarded, reducing the number of measurements and enhancing the quality of reconstructed images.
1 = T1, that is, the first GCA remains as the original, since the AF needs feedback. After the second snapshot some measurements still remain saturated. The effect of the AF improves the quality of reconstructed images when the remaining saturated measurements are discarded. The measurements that continue to be saturated in each snapshot are discarded, reducing the number of measurements and enhancing the quality of reconstructed images.
The adaptive estimation of GCA-CASSI improves the sensing. This gain in the detector is denominated "high dynamic range". More specifically, high dynamic range is the characteristic of the GCA-CASSI that allows sensing areas with low and high irradiance. The low irradiance areas are correctly measured taking advantages of the inhomogeneous illumination. In addition, high irradiance areas are adequately measured due to the GCA attenuation after each snapshot. For that reason, the GCA-CASSI is a system with high dynamic range due to its ability to adapt to inhomogeneous illumination, sensing adequately the compressive measurements.
Spectral image reconstruction
CS theory establishes that a spectral signal F ∈ 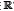 NXNXL or its vector representation ƒ∈
NXNXL or its vector representation ƒ∈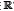 N.N.L is S- sparse in some basis Ψ, such that f= Ψθ can be approximated by a linear combination of S vectors of Ψ with S « N2L. Then, ƒ can be reconstructed from d random projections with high probability when d ≥ S log N2L«;N2L . In CASSI the compressive measurements can be represented in matrix form such that H is a matrix of size N (N + L-1)(N2L) whose structure is determined by the coded apertures and the dispersive element. Similarly, multi-shot CASSI is represented as yl = Hiƒ, where Hl represents the effect of the lth coded aperture (Arguello and Arce, 2011). The set of K compressive measurements with a distinct coded aperture is then assembled as y |=yot ,...yk-1T|T. The CASSI projections can be represented alternatively as y = HΨθ, where the matrix A = HΨ is the sensing matrix. The reconstructed data cube is obtained as ƒ = ΨargminθHΨθ2+toθ1 where H =| |H OT,... Hk-1T | , θ is a S- sparse representation of ƒ on the basis Ψ, and t is a constant of regularization. Let
N.N.L is S- sparse in some basis Ψ, such that f= Ψθ can be approximated by a linear combination of S vectors of Ψ with S « N2L. Then, ƒ can be reconstructed from d random projections with high probability when d ≥ S log N2L«;N2L . In CASSI the compressive measurements can be represented in matrix form such that H is a matrix of size N (N + L-1)(N2L) whose structure is determined by the coded apertures and the dispersive element. Similarly, multi-shot CASSI is represented as yl = Hiƒ, where Hl represents the effect of the lth coded aperture (Arguello and Arce, 2011). The set of K compressive measurements with a distinct coded aperture is then assembled as y |=yot ,...yk-1T|T. The CASSI projections can be represented alternatively as y = HΨθ, where the matrix A = HΨ is the sensing matrix. The reconstructed data cube is obtained as ƒ = ΨargminθHΨθ2+toθ1 where H =| |H OT,... Hk-1T | , θ is a S- sparse representation of ƒ on the basis Ψ, and t is a constant of regularization. Let 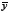 be the measurement vector with no saturated entries whose length is
be the measurement vector with no saturated entries whose length is 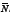 where
where 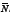 /< N (N + L-1). The matrix
/< N (N + L-1). The matrix 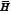 is created by adaptively selecting the non saturated rows of the matrix H. The reconstructed data cube is obtained as ƒ = ΨargminθHΨ2 +tθ1 (Laska, et al, 2011).
is created by adaptively selecting the non saturated rows of the matrix H. The reconstructed data cube is obtained as ƒ = ΨargminθHΨ2 +tθ1 (Laska, et al, 2011).
Simulation results
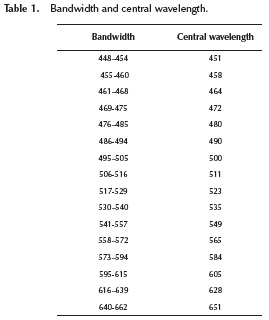
In this section the CASSI with grayscale-adaptive coded apertures is compared against the traditional CASSI with BCA. A set of compressive measurements is simulated using the models in Equation (7) and Equation (11). The measurements were constructed using a test spectral database obtained using a wide-band Xenon lamp as the light source, and a visible monochromator, which spans the spectral range between 450nm and 650nm. The image intensity was captured using a CCD camera exhibiting 256 x 256 pixels. The simulations are performed in a desktop architecture with an Intel i7-4770 3.4 Ghz processor, 32 GB of RAM memory and using Matlab R2012b. The test data cube F with 256 x 256 pixels of spatial resolution and L = 16 spectral bands is shown in Figure 5, and Table 1 shows the bandwidth and the central wavelength of each spectral band.
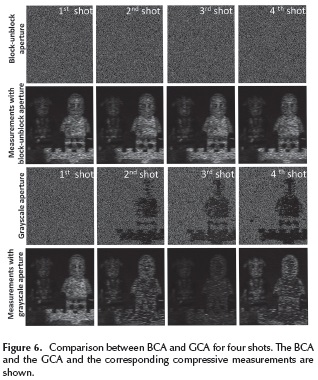
The BCA entries are realizations of a Bernoulli random variable such that the transmittance of each pattern is 25 %. The entries of the GCA are random realizations of block, unblock and attenuation elements, such that the transmittance in the first shot is 25 % and it is updated in the following shots by the AF, following Equation (11). The number of saturated pixels in the measurements is varied from 0 % to 10 %. The coded apertures are designed to have 256 x 256 pixels of spatial resolution. The CS reconstruction is carried out using the algorithm Gradient Projection for Sparse Reconstruction (GPSR) (Figueiredo, et al, 2007). The basis representation Ψis set as the Kronecker product of two basis Ψ =Ψ1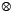 Ψ2 where Ψ1 playing the role of spatial sparsifier is the 2D-Wavelet Symmlet 8 basis, and Ψ2 being the spectral sparsifier is the 1D-DCT basis. Figure 6 shows four snapshots using the BCA and the GCA. The silhouette of the compressive saturated measurements can be observed in the grayscale-adaptive coded aperture after the first snapshot. The resulting silhouette occurs when the weighted matrix attenuates the pixels in the coded aperture, which are responsible for saturated values in the compressive measurements.
Ψ2 where Ψ1 playing the role of spatial sparsifier is the 2D-Wavelet Symmlet 8 basis, and Ψ2 being the spectral sparsifier is the 1D-DCT basis. Figure 6 shows four snapshots using the BCA and the GCA. The silhouette of the compressive saturated measurements can be observed in the grayscale-adaptive coded aperture after the first snapshot. The resulting silhouette occurs when the weighted matrix attenuates the pixels in the coded aperture, which are responsible for saturated values in the compressive measurements.
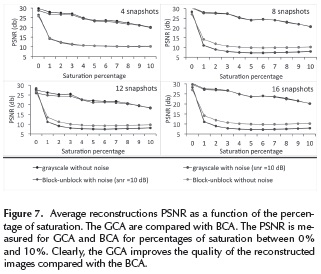
Figure 7 shows the average reconstruction peak signal to noise ratio (PSNR) as a function of the percentage of saturation. The grayscale adaptive and the BCA are compared for two, four, six, and eight snapshots. In both cases noiseless and with noise tests were included. Noiseless simulations are important because they show the system in ideal conditions. In contrast, noise simulation illustrated the system in a real scenario, in which the measurements were affected with gaussian noise with SNR = 10 dB. GCA outperforms in up to 11 dB the BCA when the number of saturated measurements is increased.
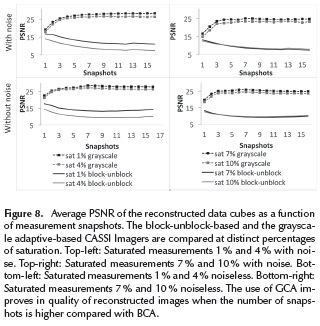
Figure 8 shows the average PSNR of the reconstructed data cubes as a function of the number of snapshots. The GCA is compared with BCA for distinct number of snapshots and variation of FPA saturation. The improvement of the proposed optical architecture can be quantified by averaging the PSNR of the reconstructed datacubes. GCA outperform in up to 11 dBs the BCA when the number of snapshots is increased.
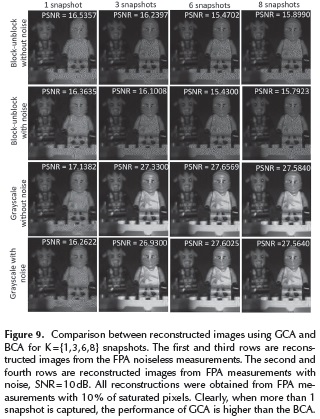
Figure 9 shows a comparison between reconstructed images using GCA and BCA where the number of snapshots varies between K = {1,3,6,8}. The BCA and GCA reconstructed images are compared including white noise in the measurements where SNR = 10 dB. All reconstructions are obtained from FPA measurements with 10 % of saturated pixels. For 1 snapshot there are no significant differences in PSNR between the BCA and the GCA, since both architectures use BCA for the first snapshot. Clearly, when more than 1 snapshot is captured, the GCA outperforms the BCA in up to 11 dB in the quality of the reconstructed images. The higher the number of snapshots, the higher the quality of reconstructed images up to 30 dB.
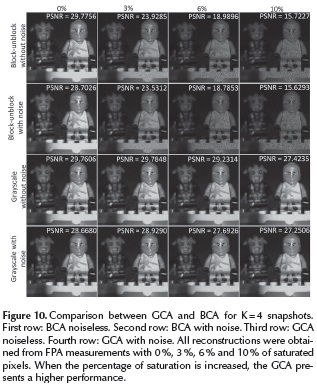
Figure 10 shows a comparison between GCA and BCA where 4 snapshots were captured. This time, the FPA measurements were saturated with 0 %, 3 %, 6 % and 10 % of saturated pixels. The GCA outperforms the BCA in up to 11 dB in the quality of reconstructed images. The GCA tolerates increments in the percentage of saturation better than BCA. When the percentage of saturation is 0 % the quality of the reconstructed image is similar between GCA and BCA due to the fact that AF is inactive.
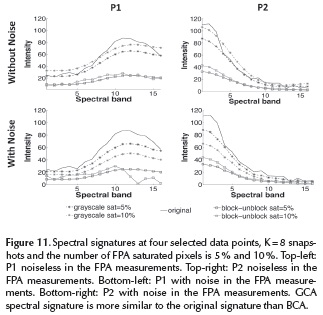
The resulting reconstructed data cubes curves are compared against their respective ground truth curves from the database. In addition, to evaluate the spectral reconstruction performance, 2 spatial points were randomly chosen and the spectral signatures are plotted in Figure 11 where 8 snapshots were captured and the number of saturated pixels in the FPA measurements is 5 % and 10 %.
According to Figure 11, GCA spectral signatures are more similar to the original signature than those obtained with the BCA.
Conclusions
GCA has been introduced in compressive spectral imaging system CASSI to replace the traditional BCA. The proposed architecture allows to attenuate the effects of the saturation of the FPA sensors. The saturation in CASSI depends on high irradiance that enters into the system overcoming the dynamic range of the sensor. The adaptive grayscale coded aperture deals with high irradiance attenuating it. The proposed technique has advantages in sensing the high irradiance but also the low irradiances, which means that the GCA-CASSI has a high dynamic range compared with BCA-CASSI. The designed GCA outperforms the BCA in up to 11 dB in the quality of the reconstructed images. The proposed adaptive filter can be implemented in PC realtime approach.
Acknowledgments
This work was supported by the Vicerrectoría de Investigación y Extensión of the Universidad Industrial de Santander, under the grant No. 1802.
References
Arguello, H. and Arce, G. R. (2011). Code aperture optimization for spectrally agile compressive imaging, J. Opt. Soc. Am. A, Vol. 28(11), 2400-2413, DOI: 10.1364/ josaa.28.002400. [ Links ]
Arguello, H., Arce, G. R. (2014). Colored coded aperture design by concentration of measurement in compressive spectral imaging. Image Processing, IEEE Transactions on, 23(4). 1896-1908. DOI: 10.1109/TIP.2014.2310125. [ Links ]
Arguello, H., Arce, G. R. (2013). Rank minimization coded aperture design for spectrally selective compressive imaging. Image Processing, IEEE Transactions on, 22 (3), 941-954. DOI: 10.1109/TIP.2012.2222899. [ Links ]
Baraniuk, R. (2007). Compressive sensing. IEEE Signal Processing Magazine, 24(4), 118-121. DOI: 10.1109/MSP.2007.4286571. [ Links ]
Candes, E. J. (2007). Compressive sampling, Proceedings of the International Congress of Mathematics, 3, 1433-1452. DOI: 10.4171/022-3/69. [ Links ]
Donoho, D. Compressed sensing. IEEE Transactions on Information Theory, 52 (4), 1289-1306. DOI: 10.1109/TIT.2006.871582. [ Links ]
Figueiredo, M.A.T., Nowak, R.D., and Wright, S.J. (2007). Gradient Projection for Sparse Reconstruction: Application to Compressed Sensing and Other Inverse Problems, IEEE Journal of Selected Topics in Signal Processing, 4(1), 586597. DOI: 10.1109/JSTSP.2007.910281. [ Links ]
Kittle, D., Choi K., Wagadarikar A. and Brady, D. J. (2010). Multiframe image estimation for coded aperture snapshot spectral imagers, Appl. Opt., 49 (36), 6824-6833. DOI: 10.1364/AO.49.006824. [ Links ]
Laska, J. N., Boufounos, P. T., Davenport, M. A., and Baraniuk, Richard. G. (2011). Democracy in action: Quantization, saturation, and compressive sensing, 31(3), 429-443. [ Links ]
Rueda, H, Arguello, H. (2013). Spatial super-resolution in coded aperture-based optical compressive hyperspectral imaging systems, Revista Facultad de Ingeniería Universidad de Antioquia, (67), 7-18. [ Links ]
Rueda, H, Parada, A, Arguello, H. (2014). Spectral resolution enhancement of hyperspectral imagery by a multiple-aperture compressive optical imaging system, Revista Ingeniería e investigación Universidad Nacional de Colombia, 34 (3), 50-55. [ Links ]
Wagadarikar, A. A., John, R., Willet, R., and Brady, D. (2008). Single disperser design for coded aperture snapshot spectral imaging, Appl. Opt., 47(10), B44-B51. DOI: 10.1364/AO.47.000B44. [ Links ]
Wu, Y., Mirza, I. O., Arce, G. R. and Prather, D. W. (2011). Development of a digital-micromirror-device-based multishot snapshot spectral imaging system, Opt., Lett., 36(14), 2692-2694. DOI: 10.1364/OL.36.00269. [ Links ]