Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.35 no.3 Bogotá Sept./Dec. 2015
https://doi.org/10.15446/ing.investig.v35n3.51750
DOI: http://dx.doi.org/10.15446/ing.investig.v35n3.51750.
Simple generation of threshold for images binarization on FPGA
Generación simple de umbral para binarización de imágenes en FPGA
E. Ieno1, L.M. Garcés2, A.J. Cabrera3, and T.C. Pimenta4
1 Egídio Ieno Júnior: B.Sc. in Electrical Engineering and M.Sc. in Telecommunications, Instituto Nacional de Telecomunicagóes (INATEL), Santa Rita do Sapucaí, Minas Gerais, Brasil. Affiliation: Mechatronics Department (DMCVG), Centro Federal de Educagáo Tecnológica (CEFET), Brasil.E-mail: egidio@varginha.cefet-mg.br.
2 Luis Manuel Garcés Socarrás: B.Sc. in Automation Engineering and M.Sc. in Digital Systems, Instituto Superior Politécnico "José Antonio Echeverría" (CU-JAE), Havana, Cuba. Affiliation: Automation and Computation Department (ISPJAE), Instituto Superior Politécnico "José Antonio Echeverría" (CUJAE), Cuba.
E-mail: lmgarcess@electrica.cujae.edu.cu.
3 Alejandro José Cabrera Sarmiento: B. Sc. and M.Sc. in Electrical Engineering, Instituto Superior Politécnico "José Antonio Echeverría" (CUJAE), Havana, Cuba. D. Sc. in Technical Sciences. Affiliation Automation and Computation Department (ISPJAE), Instituto Superior Politécnico "José Antonio Echeverría" (CUJAE), Cuba.
E-mail: alex@electrica.cujae.edu.cu.
4 Tales Cleber Pimenta: B.Sc. and M.Sc. in Electrical Engineering, Universidade Federal de Itajubá, Brasil. PhD in Electrical Engineering, Ohio University. Affiliation: Microelectronics Department (IESTI), Universidade Federal de Itajubá (UNIFEI), Minas Gerais, Brasil.
E-mail: tales@unifei.edu.br.
How to cite: Ieno, E., Garcés, L.M., Cabrera, A.J., & Pimenta, T.C. (2015). Simple generation of threshold for images binarization on FPGA. Ingeniería e Investigación, 35(3), 69-75. DOI: http://dx.doi.org/10.15446/ing.investig.v35n3.51750.
ABSTRACT
The methodologies presented in scientific literature to calculate the threshold of an image binarization process do not present good results for all types of images. Additionally, the hardware implementations do not consider the FPGA resources that are used in other processing phases. Thus, the method proposed in this work aims to present good results in the binarization process with under-resourced area of FPGA. Therefore, this paper proposes the FPGA implementation of a threshold algorithm used in the process of image binarization by simple mathematical calculations. The implementation only needs one image iteration and its processing time depends on the size of the image. The threshold values of different images obtained through the FPGA implementation are compared with those obtained by Otsu's method, showing the differences and the visual results of binarization using both methods. The hardware implementation of the algorithm is performed by a model-based design supported by the MATLAB®/Simulink® and Xilinx System Generator® tools. The results of the implementation proposal are presented in terms of resource consumption and maximum operating frequency in a Spartan-6 FPGA-based development board. The experimental results are obtained in cosimulation system and show the effectiveness of the proposed method.
Keywords: Digital image processing, threshold, FPGA, System Generator®, Matlab®/Simulink®.
RESUMEN
Las metodologías desarrolladas para el cálculo del valor de umbral empleado durante el proceso de binarización de imágenes no presentan buenos resultados para todo tipo de imágenes. Además, las implementaciones hardware no consideran los recursos del FPGA empleados en las restantes etapas del sistema de procesado. De esta forma, el método propuesto en este artículo busca alcanzar una relación óptima entre los resultados del proceso de binarización y el consumo de recursos del FPGA. Por lo tanto, este trabajo propone la implementación sobre FPGA de un algoritmo para obtener el umbral de una imagen utilizando cálculos matemáticos sencillos. La implementación se caracteriza por necesitar solamente una iteración de la imagen y su tiempo de procesamiento depende del tamaño de la imagen. Los valores de umbral obtenidos a través de la aplicación en la FPGA se comparan con los obtenidos mediante el método de Otsu, mostrando las diferencias existentes así como los resultados visuales de la binarización de diferentes imágenes utilizando ambos métodos. La implementación hardware del algoritmo de umbralización se realiza mediante la metodología de diseño basado en modelos soportada por las herramientas MATLAB®/Simulink® y Xilinx System Generator®. Los resultados de la implementación propuesta se presentan en términos de consumo de recursos y de frecuencia máxima de operación, empleando una placa de desarrollo basada en un FPGA Spartan-6. Los resultados experimentales se obtienen en régimen de cosimulación y muestran la efectividad del método propuesto.
Palabras clave: Procesamiento digital de imágenes, umbral, FPGA, System Generator®, Matlab®/Simulink®.
Received: July 7th 2015 Accepted: October 8th 2015
Introduction
Image analysis usually refers to processing of images with the goal of finding what objects are presented in the image. One of the most widely used techniques for segmenting the objects in an image is binarization (Gonzalez and Woods, 2009). In this technique, each pixel is compared to a threshold separating the foreground and background in an image. The output of the thresholding operation is a binary image. The uses of a bi-level information decrease the computational load and enable the utilization of the simplified analysis methods compared to 256 levels of grayscale or color image information. For instance, in document image analysis, where the goal is to extract printed characters, the foreground can be represented by gray-level 0, that is, black for text; and background by the highest luminance for document paper, that is 255 in 8-bit images, or conversely: foreground by white and background by black.
Another application of this technique is the motion detection where the binarized image simplifies the count, distance calculations and dimensioning of moving objects (Das and Saharia, 2014; Liang, Haili, Tao, and Xiaomei, 2014; Pushpa and Sheshadri, 2014). Other areas such as the processing of static medical images using the binarization process presented in Humayun, Malik, and Kamel, (2011) use several thresholds to segment the injured area of the skin and improve medical diagnosis.
There are several algorithms in scientific literature aiming at the binarization process. However, the lack of objective measures to evaluate the performance of binarization algorithms and difficulties in performing tests in an single environment, where all types of algorithms for the same purpose can be tested, motivated the study presented in Sezgin and Sankur, (2004). This analysis is an attempt to develop a unified note to the variety of binarization algorithms. In this study, 40 methods to find the best threshold are analyzed and classified. According to this study, there is the large number of good algorithms to calculate the threshold for binarization of an image. However, it may not be stated that one of the methods presents a satisfactory result for processing all kinds of images, such as images that may present uneven lighting problems and objects at different gray-levels, among others.
Studies on image binarization described in Sezgin and Sankur, (2004) consider that the Otsu's method is one of the best in determining the threshold. Otsu's method (Otsu, 1979) is a popular technique for automatic global thresholding, which can be used in a wide range of application, such as vehicle license plates recognition (LPR), preprocessing fingerprint image and separation and identification of skin lesions, among others. This method is developed through statistical calculations of mean and variance by image histogram in order to find the threshold value.
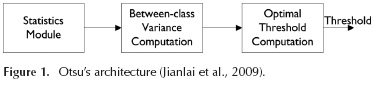
The threshold calculated by Otsu's method is considered optimal to maximize the variance between classes, where these classes represent an assignment of pixels to two or more groups. The initial operation is to calculate a value that provides the best separation between classes. For this operation, the intensity values of the pixels are used (Gonzalez, Woods, and Eddins, 2009). Figure 1 shows the computational steps developed in Otsu's method.
In the Statistics Module (Figure 1), four functions are carried out: the histogram calculation, the cumulative histogram, the intensity area calculation and the accumulated intensity area. All four functions are based on the histogram and used to calculate the variance of the two classes (Jianlai, Chunling, Min, and Changhui, 2009).
The Optimal Threshold Computation module (Figure 1) is responsible for carrying out the comparison process to choose the maximum variance between classes and inform the optimal threshold through the corresponding index (Jianlai et al., 2009).
The Otsu's method and their approaches implemented on FPGA (Field Programmable Gate Array) produce satisfactory results in terms of speed and resource consumption when analyzed individually (Ashari and Hornsey, 2004; Jianlai et al., 2009; Tian, Lam, and Srikanthan, 2003). However, the implementation of statistical calculations based on the histogram for some types of images, can provide similar results to other methods, therefore using more resources of the FPGA. Furthermore, the process for obtaining the threshold is only part of the binarization stage, which is one of the simplest steps of an image processing system. For example, processing systems may require memory capacity to store a database used in the interpretation of data in high-level steps, which have occupied part of the histogram calculations. Thus, it proposes the development of an algorithm to calculate the threshold in FPGA aiming at mathematical simplicity, reduction of occupied resources and values near the Otsu's method. Hence, the aim of this paper is to present a hardware alternative solution to calculate the threshold value in only one image iteration and automatically set this parameter to the binarization block for the image process.
In order to check the results of the binarized images, the article presents the visual results and calculates the values in the hardware implementation over a group of 10 images with different characteristics, which are compared with the threshold calculated by Otsu's method.
Implementation methodology
The implementation methodology used in Areefabegam and Narendrakumar, (2014); Hamdaoui (2013); Saidani . (2009) is employed in this work, adding the hardware simulation results with area resources and speed optimization. In this methodology, the image processing is implemented by the Xilinx System Generator® (XSG) using model-based design techniques in MATLAB®/Simulink® software. Hence, continuous simulation during project development and automatic code generation for the target architecture, tend to decrease development time. The image processing performed with XSG allows the use of optimizable and configurable blocks according to the need of the designer. This tool also permits the development and implementation of embedded systems without thorough knowledge of hardware programming languages (Albaladejo, Andrés, Lemus, and Salvi, 2004; Ramos-Arreguín et al., 2010).
MATLAB®/Simulink® software, as a simulation and development tool based on models, presents a graphical environment and a series of configurable blocks with partial solutions for some applications, including image processing. Furthermore, the synthesis tool System Generator® with Simulink® library enables the automatic generation of code, such as VHDL.
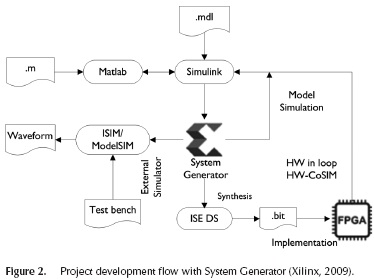
Figure 2 shows the flow of the project through the MATLAB®, Simulink®, Xilinx System Generator® and ModelSIMTM. XSG model-based design flow provides the interface between Simulink® models and Xilinx tools for reconfigurable devices. The Simulink® model (.mdl) describing the system is compiled by XSG for simulation using Simulink® internal or external simulators. ISE implementation tools obtain the configuration (.bit) file to program the FPGA.
XSG offers three ways for the verification of the design: functional simulation with Simulink®, functional and temporal HDL simulations using ISIM or ModelSIMTM simulators, and HW co-simulation, where the HW part of the design is implemented on a FPGA development board and interacts with the rest of the Simulink® model. This option creates a configuration file for the target device and associates it to a new Simulink® block. The process allows checking the algorithm functionality using HW in the loop.
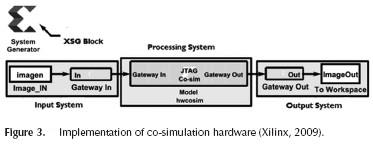
The realization of the hardware co-simulation is achieved through the XSG block ISE version 14.7 that performs the compilation of the processing system. In the configuration, the board and the connection interface with the development board is selected. Thus, once the compilation is completed, the system creates a new block called Model hwcosim to be replaced in the processing system as presented in Figure 3. The XSG is in charge of the synthesis, routing and processed system configuration in the connected board (Ramos-Arreguin et al., 2010). Therefore, there is an inflow of the data from MATLAB® workspace to the board, which is processed by the hardware and returns to MATLAB®.
The difference between the simulation and co-simulation does not display the functional outcome, but does display the difference between the response times. This is because the synthesis influences the placement and routing of the specific logic blocks of each physical device.
Development methodology
For the calculation of the threshold of multiple images by Otsu's method, the MATLAB® function is used. These values are collected and compared with the FPGA implementation.
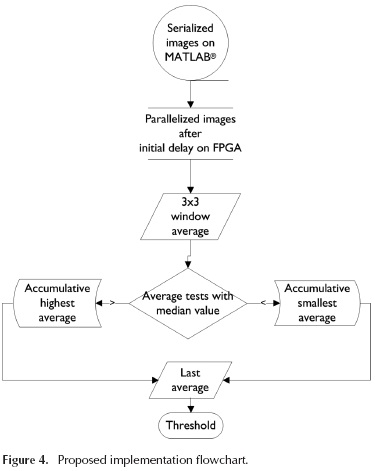
Figure 4 presents the proposed steps for threshold computation using a flowchart. It displays the use of simple mathematical operations aiming to the use of a small number of resources of the FPGA. The basic idea is to separate the calculations of each average 3x3 window into the highest and smallest values. These values are separated by the median value between 0 and 255. The last average computed after processing the entire image sets the threshold value.
In the iterative method presented in Gonzalez and Woods, (2009), when the image background and the objects fill a comparable size of areas, a good initial value for the threshold is the average of gray-levels. Thus, for the area occupied by small objects compared with the image background, the average level is not the most appropriate choice. Hence, the most appropriate value for the threshold in these cases will be the median value between minimum and maximum gray-levels. Therefore, this choice restricts the application of the proposed method for specific types of images.
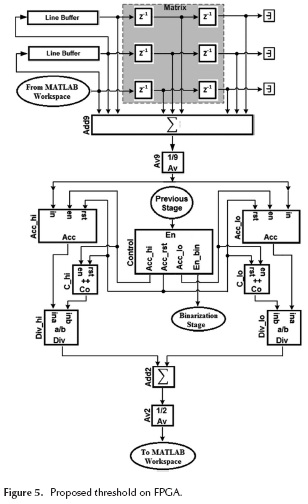
Figure 5 shows the proposed implementation on FPGA. Initially, the image is loaded via a MATLAB® script (From MATLAB Work-space), which converts a matrix in a column vector containing all the pixels information to emulate a real image stream. However, the operation performed by the adder block (Add9) with the 3x3 window requires 9 pixels simultaneously available at its inputs. Thus, in order to process these pixels at the same time, an initial delay (Line Buffer) is needed to store two lines of the images. This block and a matrix of register blocks (Matrix), perform the parallelization of the 3x3 window passing over the image received from MATLAB® workspace. The delay to obtain 9 valid pixels at the adder block is function of the number of columns of the original image and the size of the processing window (2x Number of Col-umns + 2).
The control block (Control) is responsible for generating signals that separate the accumulated values by comparing them with middle gray-level. This block receives the input signal (Previous Stage) that enables the internal blocks. Hence, when the first sum (Add9) operation is performed using the valid data, a reset signal (Acc_rst) is sent to the accumulators (Acc_hi and Acc_lo)) and counter (C_hi and C_lo) blocks. These accumulators store the sums of the highest (Acc_hi) and smallest (Acc_lo) averages obtained for each 3x3 window in the image. In addition, it is used to enable a signal to split the accumulation between the highest and smallest values, which are initially present at the inputs of both accumulators. As the number of accumulated operations is unknown, the signals enable the specific counter for the highest (C_hi) and smallest (C_lo) averages. This number is used to perform the arithmetic average of the accumulated values.
The division blocks (Div_hi and Div_lo) perform the arithmetic average of the accumulated values. Thus, the results of division blocks are added (Add2) and divided (Av2) to compute the final arithmetic average. After calculating the last average between the highest and smallest accumulated values, the valid threshold signal (En_bin) is generated, allowing the synchronization of the binarization stage. Finally, this value is sent to MATLAB® (To MATLAB Workspace) in order to be analyzed via a script.
The presented method performs iterative calculations with windows only once on the all image, while maintaining an initial fixed threshold in the middle gray-level. Hence, the stopping criterion is the processing of the last pixel. This criterion is adopted because the operations repeatedly carried in all image pixels can derail the real-time processing.
Implementation results
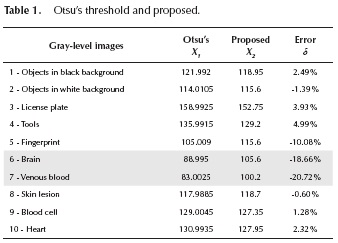
The implementation is developed in a Spartan-6 FPGA-based board, where the resources consumption with the smaller and the bigger image are analyzed. The images used in this article are available in MATLAB® library and others were obtained from the research team library. The pictures chosen have different characteristics that can evaluate the precision of the algorithm compared to the Otsu's method. The relative error (l) is used in order to check the difference between the results of both methods, where δ is the relative error, X1 is the value calculated by Otsu's method and X2 is the value obtained by the proposed method. The approximation error (X1-X2) is the discrepancy between the value calculated by Otsu's method and the proposed.
The relative error is the approximation error divided by the magnitude of the expected value. Hence, the negative values represent more quantity of pixels than the expected value in the background, and, otherwise, in the foreground of the binarized image.
Table 1 shows the description of each image, the resulting threshold calculated by Otsu's method on MATLAB® and the proposed method on FPGA. In addition, it presents the percentage difference between these values. The highlighted results in the Table 1 show the values that have a higher relative error. These differences represent features in the image that have been lost, being characterized as background.
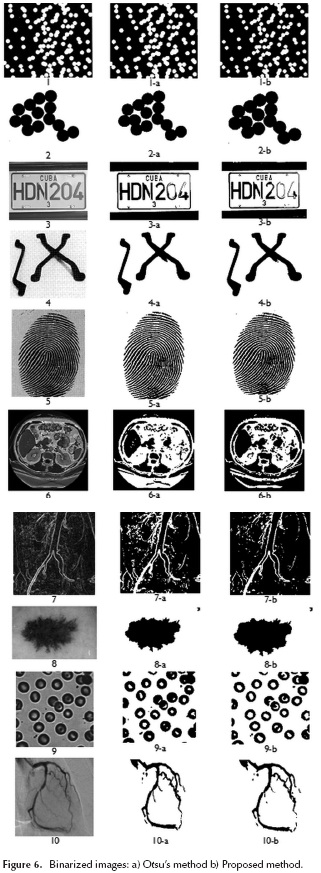
Figure 6 shows the original image, obtained by binarization using the threshold by Otsu's method and through implementation proposal. The visual perception of these losses are used to just have an idea of the results, since this type of analysis is very subjective.
Table 1 shows that results of threshold for pictures 1, 2, 3, 4, 5, 8, 9 and 10 are close to the Otsu's method threshold value. Furthermore, significant losses are not observed for these images in Figure 6. Even though for images 6 and 7 the threshold calculated by the proposed method is further than that presented by the Otsu's method, displaying losses can be considered irrelevant for some practical applications. Hence, the results do not compromise the use of the proposed method in practical applications such as identification and counting of objects.
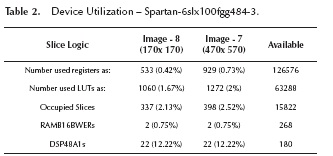
Table 2 shows the resources employed in the Spartan-6 FPGA-based development board (6slx100fgg484). The implementation is applied to the smaller image (Figures 6 and 8 170x170 pixels) and the bigger image (Figures 6 and 7 470x570 pixels).
Among the blocks used for implementation on FPGA, the division blocks have the highest possibility to improve system response time. Additionally, working with binary representation in fixed-point number and operands with fewer bits results in approaches that improve implementation performance. Thus, the division operation by 2-based power (Av2) implemented on FPGA employs shift register that is faster and consumes fewer resources than the division specific blocks. However, the division operation on the accumulated results have not dividend previously known, which leads to increased complexity of these implemented blocks. Therefore, specific blocks of division are also implemented.
The division specific block in XSG library has the option to select between two algorithms to perform the operation. The Radix2 algorithm is recommended for operand widths less than 16 bits. This option supports both unsigned (2's complement) and signed divisor. The HighRadix algorithm is recommended for operand widths greater than 16 bits, although the implementation requires the use of DSP48 specific blocks. This option only supports signed (2's complement) divisor and dividend inputs (Xilinx, 2009).
Therefore, as in the proposed implementation the number of bits representing the result of the accumulator is directly proportional to the image size, the maximum frequency is around 50 MHz for the division specific block with High Radix. In order to increase the system operating frequency, the algorithm used by the divisor to calculate the cumulative average is changed to Radix2. In this situation, the frequency is significantly increased to 184.076 MHz. However, the division is limited to integer numbers with up to 16 bits, reducing the size of the image processed. On the other hand, even with the reduction of three times the operating frequency using the HighRadix algorithm, there is the advantage of working with bigger images.
Conclusions
In this paper an algorithm to calculate the threshold for image binarization using simple mathematical calculations over a 3x3 window was proposed. It provides a new threshold when the windows move to another region of the image. The processing window allows to analyze 9 pixels at the same time, instead of performing pixel-by-pixel operations. Thus, through arithmetic average calculation, it is possible to obtain results close to Otsu's method.
Since the classification by the visual inspection is sometimes subjective to each person observing the same image, there is no way to say which is the best result. However, the proposed method allows to obtain a threshold for images binarization with under-resourced area of FPGA. The results demonstrate that the presented method offers better performance on images with homogeneously distributed objects on a uniform background.
The use of System Generator model-based design flow to implement the proposed algorithm speeds-up the development time adding some abstraction levels to traditional design flows using accurate simulations and easily parametrizable blocks. Thus, this tool allows rapid changes in the implementation aimed to the optimization of the relation of execution speed and occupied area in the device.
Acknowledgements
The authors acknowledge FAPEMIG, CNPq and CAPES, a Brazilian Government entity focused on the training of human resources, for their financial support.
References
Albaladejo, J., de Andrés, D., Lemus, L., & Salvi, J. (2004). Codesign Methodology for Computer Vision Applications. Microprocessors and Microsystems, (5-6), 303-316. DOI:10.1016/j.micpro.2004.-03.010. [ Links ]
Areefabegam, S. K., & Narendrakumar, T. (2014). FPGA Based Design and Implementation of Image Edge Detection Using Xilinx System Generator. International Journal of New Trends in Electronics and Comunication, 2,18-21. [ Links ]
Ashari, E., & Hornsey, R. I. (2004). FPGA Implementation of Real-Time Adaptive Image Thresholding. In J. C. Armitage, R. A. Lessard, & G. A. Lampropoulos (Eds.), (pp. 410-419). DOI:10.1117/12.566861. [ Links ]
Das, D., & Saharia, S. (2014). Implementation and Performance Evaluation of Background Subtraction Algorithms. International Journal on Computational Sciences & Applications (IJCSA), 4 (2), 49-55. DOI:10.5121/ijcsa.2014.4206. [ Links ]
Gonzalez, R. C., & Woods, R. E. (2009). (3rd ed.). Tennessee: Prentice Hall. [ Links ]
Gonzalez, R. C., Woods, R. E., & Eddins, S. L. (2009). (2nd ed.). Gatesmark. [ Links ]
Hamdaoui, F., Khalifa, A., Sakly, A., & Mtibaa, A. (2013). Real Time Implementation of Medical Images Segmentation Based on PSO. In 2013 International Conference on Control, Decision and Information Technologies (CoDIT) (pp. 36-42). Hammamet, Tunisia: IEEE. DOI:10.1109/ CoDIT.2013.6689516. [ Links ]
Humayun, J., Malik, A. S., & Kamel, N. (2011). Multilevel Thresholding for Segmentation of Pigmented Skin Lesions. In 2011 IEEE International Conference on Imaging Systems and Techniques (pp. 310-314). IEEE. DOI:10.1109/IST.2011.5962214. [ Links ]
Jianlai, W., Chunling, Y., Min, Z., & Changhui, W. (2009). Implementation of Otsu's Thresholding Process Based on FPGA. In (Vol. 1, pp. 479-483). IEEE. DOI:10.1109/ICIEA.2009.5138252. [ Links ]
LLiang, Z., Haili, W., Tao, D., & Xiaomei, H. E. (2014). Improving Integrality of Detected Moving Objects Based on Image Matting. Chinese Journal of Electronics, 23(4), 742-746. [ Links ]
Otsu, N. (1979). A Threshold Selection Method from Gray-Level Histograms. IEEE Transactions on Systems, Man, and Cybernetics, 9(1), 62-66. DOI:10.1109/TSMC.1979.4310076. [ Links ]
Pushpa, D., & Sheshadri, H. S. (2014). Computationally Efficient Al-gorithm for Detecting Moving Objects with Moving Background. International Journal on Recent and Innovation Trends in Computing and Communication (IJRITCC), 2(11), 3605-3610. [ Links ]
Ramos-Arreguin, C. A., Moya-Morales, J. C., Ramos-Arreguin, J. M., Pedraza-Ortega, J. C., Canchola-Magdaleno, S. L., & Vrgas-Soto, J. E. (2010). Metodología de una Etapa Básica de un Sistema de Procesamiento de Imágenes Basado en FPGA. In 9o Congreso Nacional de Mecatrónica, Puebla, México (pp. 235-240). Puebla, México. [ Links ]
Saidani, T., Dia, D., Elhamzi, W., Atri, M., S Tourki, R. (2009). Hardware Cosimulation for Video Processing Using Xilinx System Generator., 3-7. [ Links ]
Saidani, T., Dia, D., Elhamzi, W., Atri, M., S Tourki, R. (2009). Hardware Co-simulation for Video Processing Using Xilinx System Generator. Proceedings of the Word Congress on Engineering, I, 3-7. [ Links ]
Sezgin, M., S Sankur, B. (2004). Survey over Image Thresholding Techniques and Quantitative Performance Evaluation. Journal of Electronic Imaging, 13(1), 146-168. Doi:10.1117/1.1631315 [ Links ]
Tian, H., Lam, S. K., & Srikanthan, T. (2003). Implementing Otsu's Thresholding Process using Area-Time Efficient Logarithmic Approximation Unit. In Proceedings of the 2003 International Symposium on Circuits and Systems, 2003. ISCAS '03. (Vol. 4, pp. IV-21-IV-24). IEEE. Doi:10.1109/ISCAS.2003.1205763Xilinx. (2009). The MathWorks Design Tools and Service. Retrieved from http://www.xilinx.com. [ Links ]
Xilinx. (2009). The MathWorks Design Tools and Service. Retrieved from http://www.xilinx.com. [ Links ]