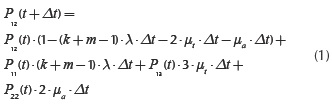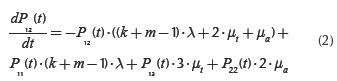Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.36 no.2 Bogotá May/Aug. 2016
https://doi.org/10.15446/ing.investig.v36n2.54210
DOI: http://dx.doi.org/10.15446/ing.investig.v36n2.54210
A simulation model of assistants' and technicians' engagement in processing generated requests at a university
Un modelo de simulación de la participación de asistentes y técnicos para procesar las solicitudes generadas en una universidad
Aleksandar Lebl1, Dragan Mitic2, Djurdje Perisic3, and Branislav Todorovic4
1 Electrical Engineer, Ph.D, IRITEL a.d., Serbia. Affiliation: Assistant Research Professor, IRITEL a.d., Serbia. E-mail: lebl@iritel.com
2 Electrical Engineer, Ph.D, IRITEL a.d., Serbia. Affiliation: Associate Research Professor, IRITEL a.d., Serbia. E-mail: mita@iritel.com
3 Electrical Engineer, Ph.D, Faculty of Information Technology University Slobomir P, Bosnia and Herzegovina. Affiliation: Full Professor, Faculty of Information Technology, University Slobomir P, Bosnia and Herzegovina. E-mail: djurdje@beotel.rs
4 Electrical Engineer, Ph.D, RT-RK, Institute for Computer Based Systems, Serbia. Affiliation: Full Research Professor, RT-RK, Institute for Computer Based Systems, Serbia. E-mail: Branislav.Todorovic@rt-rk.com
How to cite: Lebl, A., Mitic, D., Perisic, D., & Todorovic, B. (2016). A simulation model of assistants' and technicians' engagement in processing generated requests at a university. Ingeniería e Investigación, 36(2), 35-42. DOI: 10.15446/ing.investig.v36n2.54210.
ABSTRACT
This paper presents a simulation model for the optimization of assistants' and technicians' engagement in a university teaching process. This model enables us to obtain the values of important parameters for the analysis of the process; even in the case of complex processes at large university departments, which cannot be easily analyzed using analytical methods. In the case when the number of technicians available is not sufficient to process all generated requests of professors and assistants, the assistants take over the processing of the requests, which cannot be processed immediately by the technicians. The characteristics of the system are compared for three different situations: when all technicians are processing the requests of all assistants and all professors; when technicians and assistants are separated in smaller groups; and when the technicians are processing only the requests of the professors and the assistants from their group.
Keywords: Education, teaching process optimization, queueing system, simulation model, unwanted states.
RESUMEN
En este trabajo se presenta un modelo de simulación para la optimización de la participación de asistentes y técnicos en el proceso de enseñanza de una universidad. Este modelo nos permite obtener los valores de los parámetros importantes para el análisis del proceso, incluso en el caso de un proceso complejo en departamentos de universidades grandes, que no se puede analizar fácilmente utilizando métodos analíticos. Si los técnicos disponibles no son suficientes para procesar todas las solicitudes generadas por profesores y asistentes, los asistentes asumen el control la tramitación de las solicitudes, que no pueden ser procesadas inmediatamente por los técnicos. Se lleva a cabo una comparación de las características del sistema para tres situaciones diferentes: cuando los técnicos están procesando las peticiones de todos los asistentes y los profesores; cuando los técnicos y asistentes se separan en grupos más pequeños; y cuando los técnicos están procesando sólo las peticiones de los profesores y los asistentes de su grupo.
Palabras clave: Educación, optimización de procesos de enseñanza, sistema de colas, modelo de simulación, estados no deseados.
Received: May 5th 2016 Accepted: August 1st 2016
Introduction
Improvement of the teaching process in all grades of the teaching system is the subject of many papers and studies (Kotnour, 1999; Pardede et al., 2012; Aizpun et al., 2015; Nikolic et al., 2015; Bogoya et al., 2013; Siddiqi et al., 2010; Mbarika et al., 2003; Macias 2012). In these works, different aspects of the teaching process are analyzed. The contribution of Kotnour (1999) is the description and evaluation of an organizational learning teaching process. In Pardede (2012), the focus is on reviewing and aligning the assessment tasks to ensure an effective evaluation and the achievement of student learning outcomes. Aizpun et al. (2015) emphasize the importance of stimulating students' creativity and analyzes University-Industry collaboration as one of the possibilities to achieve this aim. But it is not only important to improve learning methods for students, attention must be also paid to the training of teaching personnel, as is, for example, explained in Nikolic et al. (2015).
The contribution of Bogoya et al. (2013) is in proposing a new mathematical model of higher education overall effectiveness. Authors in Siddiqi et al. (2010) describe how an automated short-answer marking system can be effectively used to improve teaching and learning processes. Results in Mbarika et al. (2003) suggest that when designing new learning environments, it is important for the female students to be challenged and have opportunities for group learning. In Macias (2012), an e-portfolio is presented as an approach to improve the teaching/learning and evaluation processes in project-based learning environments.
For the process of education and high-quality knowledge adoption, the work of non-teaching staff, for example technicians, is very important, since they take part in the process of teaching preparation and realization. Some relatively simple jobs can be done by technicians, so it is not necessary that assistants are engaged on them. The assistants process the jobs if there are no free technicians, i.e. if all technicians are engaged on processing other jobs (Šuh et al., 2014). The assistants' engagement on the jobs, which can be processed by technicians, is not desirable, but if this situation does not happen very often, it can be tolerated. The moments when assistants process jobs that can be processed by technicians are called undesirable states, and their probabilities are calculated in Šuh et al. (2014). Situations when assistants still process the requests, although there are idle technicians (especially undesirable states), are separately analyzed (Šuh et al., 2014). As the analysis in Šuh et al. (2014) is performed only analytically, results can be obtained for a relatively small number of professors, assistants and technicians. Their number is limited by the total number of system states, which increases rapidly (with geometric progression) when the number of professors, assistants, and technicians increases.
Lebl et al. (2014) present the model for calculating financial expenses of processing requests by technicians and assistants. The expenses are calculated for several systems and they are compared to each other.
In this paper we present the simulation model of technicians' and assistants' engagement in the university teaching process. The mean number of engaged technicians and assistants on processing analyzed jobs is presented as the result of simulation. University teaching systems can be very large. It is very difficult, or even impossible, to analyze such great systems analytically. In that case, simulation analysis must be implemented. The goal in our research was to compare the results obtained analytically and the results obtained by our originally developed simulation method for a number of small systems. As the results obtained by these two methods agree for small systems, simulation methods can be implemented also for the greater systems (systems with greater number of professors, assistants and technicians).
Model, designations and abbreviations
Let us consider a model of teaching process, in which professors, assistants and technicians participate. The main assumptions of our model are:
- In an everyday realization of the teaching process in a faculty, some simpler requests are generated. These requests are originated from the professors' and assistants' activity.
- Technicians are enlisted in a faculty to process these requests.
- If there are a lot of requests (generated by professors and assistants), technicians are not able to process them all. In that case, some assistants take over processing part of the requests. Hence, they are not able to carry out their main tasks (meaning new requests are not generated by their activity), thus decreasing the rate of new requests being generated.
- If an assistant starts processing a request because there are no free technicians, he/she will continue processing the request until it is finished, even if some technician becomes available.
The technicians' and assistants' engagement in the teaching process can be presented using the queueing theory models. The systems from queueing theory are often analyzed in the literature. Kleinrock (1975), Filipowitz et al. (2008) and Petrovic, et al. (2008) are a small part of this literature.
Throughout the paper, the following designations and abbreviations are used:
- {i2, it} - the current state of the system where ia are assistants and it are technicians engaged in the processing of requests.
- k - number of professors who generate requests.
- m - number of assistants in the system.
- n - number of technicians in the system.
- λ- intensity of requests generation by each professor and assistant.
- µ3 - intensity of requests processing by each assistant.
- µt - intensity of requests processing by each technician.
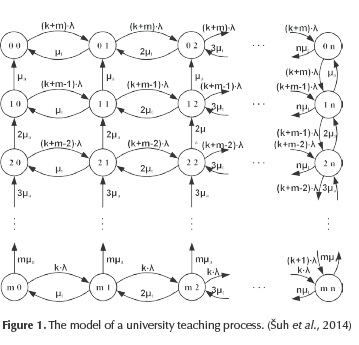
The model from queueing theory, where technicians and assistants are processing the requests, is illustrated in Figure 1. The pair of digits (p, q) (p = 0,1,...,m, q = 0,1,...,n) signify the number of assistants (the first digit) and the number of technicians (the second digit), who process the requests. Each pair of digits presents one system state. All possible transition intensities are presented between the states of the system.
The equations for the system presented in Figure 1 are constituted for each state of the system (Šuh et al., 2014). For example, let us consider the state (1,2). The probability that this system can be found in state (1,2) in time moment t+Δt is:
If Δt→0, Equation (1) can be expressed as:
The equations of the type presented by (2) can be defined for each possible state of the system, giving as the final result the matrix expression:
where P(t) is the vector of state probabilities, and A is the matrix of transition intensities between the system states.
As usual, in stationary state (when t→∞), probabilities of all states (including state (1,2)) do not change over time, so it becomes 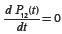 in Equation (2), or
in Equation (2), or 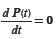 in Equation (3).
in Equation (3).
Therefore, in stationary state, matrix Equation (3) can be expressed as:
As usual in queueing systems, the normalization condition, which must be fulfilled, is 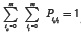 , where
, where 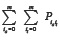 includes probabilities of all possible states of the system.
includes probabilities of all possible states of the system.
After solving system of Equations (4), which enables us to obtain probability of system states, we can determine important parameters of the system, as are the ones defined in this paper. The number of unknown values (probabilities) in the system of equations is equal to the number of possible states of the system (Petrovic et al., 2008).
Generation of the events in the system simulation
The number of possible states of the system is often very great. So, when solving the system analytically, we obtain a system of equations with a large number of unknown values, which is not calculated easily. In such situations, the simulation models of the queueing systems are very important (Rodrigues et al., 1972).
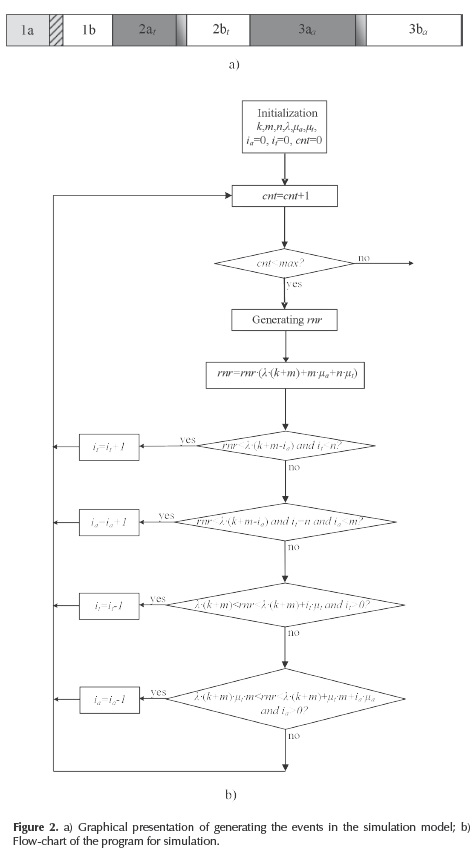
The main idea of simulation has its origin in the simulation of telephone systems (Olsson 1970, Kosten 1970). In the simulation process we start from the random number generator, which generates numbers with uniform distribution in the range 0 to 1. The random number (rnr) is multiplied by the normalization factor. The whole possible area of obtained random numbers is divided into three ranges, as presented in Figure 2a. The range 1 corresponds to the generation of new a request. The ranges 2 and 3 correspond to the completion of the processing, if a technician (range 2) or an assistant (range 3) are engaged in processing the request. Each one of the ranges 1, 2 and 3 has a constant size during the simulation, and it is divided in two parts. The function of these parts is as follows:
- If the random number is in the range 1a, the new request is generated.
- If the random number is in the range 1b, nothing happens.
- If the random number is in the range 2at, the request, which is processed by the technician, is terminated.
- If the random number is in the range 3aa, the request, which is processed by the assistant, is terminated.
- If the random number is in the range 2bt or 3ba nothing happens.
The size of the ranges 1a and 1b in Figure 2a depends on the simulation of the number of assistants, who are engaged in that moment with the processing of the requests (ia), because the assistants, who are processing the requests, cannot generate the requests at the same time. Thus, the greater number of assistants engaged in the processing of requests, reduces the size of the range 1a, and enlarges the size of the range 1b (symbolically presented by the hatched area in Figure 2a). The sizes of the ranges 2at and 3aa are directly proportional to the number of technicians (it), i.e. assistants (/a ) who are processing the requests in that moment.
The flowchart of the program for the simulation is presented in Figure 2b. In this figure only the method for the generation of the events in the simulation model is presented. The main parameters for the simulation: k, m, n, λ, µa and µt and initial values ia=0 and it= 0 are defined at the beginning of the program. The value of the counter (cnt) is an indication of how many events are generated. It is incremented after each simulation step and it is used to determine that generation of new events stops when cnt reaches its maximum value (max in Figure 2b).
The generated rnr in each simulation step is multiplied by the factor λ · (k+m) + m · µa + n · µt. The program tests in which range the generated rnr is situated, and depending on this, the new request is generated for the technician (i= / + 1) or for the assistant (ia= ia+ 1), or the termination of the processing of the request by a technician (it = it - 1) or an assistant (ia= ia - 1) is generated. Besides the condition a a that the generated rnr must be in the specific range, it is always necessary that the condition dealing with the number of engaged assistants and technicians must be fulfilled. For example, the new technician can be engaged in the processing of the request if the instantaneous number of engaged technicians is smaller than the total number of technicians at disposal (sign and it< n in Figure 2b). The new assistant would be engaged if all disposable technicians are engaged (and it = n), and the instantaneous number of assistants engaged in the processing of requests is smaller than the total number of assistants (and ia < m). The conditions, which must be checked in the case of the request termination, are if there are engaged assistants (and ia > 0), or engaged technicians (and it> 0) in the system. In all cases when the conditions for the generation of some event are not fulfilled, the execution of the program returns to the next simulation trial.
In each simulation trial at least 200000 random numbers were generated. All simulated cases were processed statistically by determination of mean values of variables and confidence interval of the obtained results.
The correctness of the simulation model is tested in such a way that its results are compared to the results obtained analytically for few, relatively simple cases. The probabilities of system states are compared at first. After that, important system parameters are determined based on analytical and simulation results. The analytical and simulation results for the probabilities of system states and for the mean number of active assistants and technicians are nearly completely equivalent.
Analysis of the obtained results
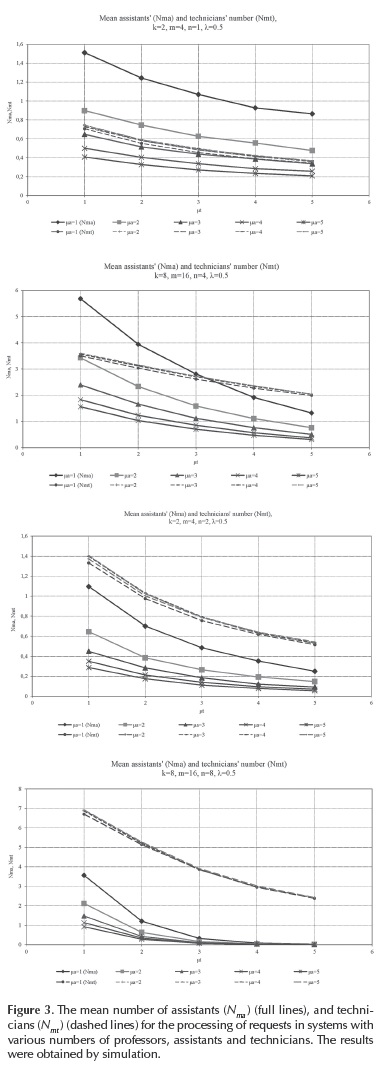
We wanted to give the answer to a few questions, using the simulation analysis. The first question was: is it better to divide all engaged technicians into smaller groups, thus providing that each group processes only the requests of a smaller group of professors and assistants; or to devote all technicians to all professors and assistants on the faculty? In order to give the answer to this question, we performed the simulation of the systems with k = 2, m = 4, n = 1, λ = 0.5 and with k = 8, m = 16, n = 4, λ = 0.5. Figure 3a, 3b, 3c, 3d, and Figure 4 present the mean values of variables obtained after four simulation trials. The elements presented as the result of simulation are the mean number of assistants and technicians (Figure 3, cases a and b) engaged in the processing of requests. The mean total number of engaged assistants and technicians for the analysis of the system with k = 2, m = 4, and n = 1 is obtained as the quadruple value read from the graphs in Figure 3, case a. In all the cases the total value obtained for number of needed assistants for the system with k = 2, m = 4, n = 1 is greater than in the case with k = 8, m = 16, n = 4, while the situation is opposite for the mean number of technicians. For example, for µt = 3 and µa = 1, the mean number of assistants for the system with k = 2, m = 4, n = 1 is Nma = 4-1.08 = 4.32, and the mean number of ma ' technicians is Nmt = 4-0.45 = 1.8. For the same values of µt and µa in the system with k = 8, m = 16, n = 4, the values are Nma = 2.8 and Nmt = 2.6. Therefore, it is better to devote all available technicians to all professors and assistants, because in that case the mean number of engaged technicians is greater, and the mean number of engaged assistants is smaller than when all assistants and technicians are divided into smaller groups. The mean number of engaged assistants on processing the requests drops from 4.32 to 2.8, or 35 %.
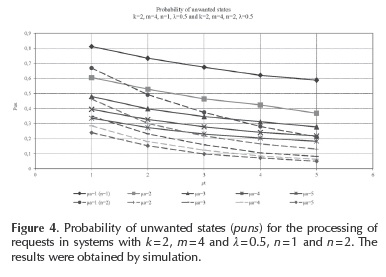
Let us consider now the situation where we introduce new technicians in the system with the same number of professors and assistants and the same intensity of generating the requests. The results of the simulation are presented in Figure 3: cases c and d, whereby case c refers to the system where technicians are split into smaller groups (k=2, m = 4, n = 2), and case d) to the system where all technicians process the demands of all professors and assistants (k = 8, m = 16, n = 8).
As in the previous analysis for n = 1, i.e. n = 4, the greater efficiency of the larger system can be proved in this case. For the same values µt = 3 and µa = 1 as in the previous case, the mean number of assistants engaged in the processing of requests for the system with k = 2, m = 4, n = 2, is Nma = 4-0.48 = 1.92; while the mean number of technicians is Nmt = 4-0.76 = 3.04 (quadruple values read on Figure 3, case c). In the system with k = 8, m = 16, n = 8 for the same values of µt and µa, the mean number of assistants is smaller, (N = 0.3), while ma the mean number of technicians is greater, (Nmt = 3.8), according to Figure 3, case d. In this case the mean number of total engaged assistants drops significantly when larger a system is implemented: from 1.92 to 0.3, or more than six times.
The second important element is the comparison of the probabilities of unwanted states (puns) when the number of engaged technicians increases, while their intensity for processing the requests remains unchanged; and in the case when the existing technicians increase the intensity of processing the existing requests. Unwanted states are the situations when at least one assistant is engaged in processing the request, and the probability of an unwanted state is the sum of probabilities of all system states when at least one assistant is engaged in processing the requests. The comparison of these values can be made according to the graph in Figure 4. The probabilities of unwanted states are presented for the system with n = 1 and n = 2, in both cases k = 2, m =4, λ = 0.5. According to the graph, for example, in the case when it is k = 2, m = 4, n = 1, µa = 1, for µt= 2, we obtain puns = 0.74. If the intensity of technicians' processing the requests increases two times (µt= 4), the probability of unwanted states decreases on puns = 0.62. If instead of this, the value stays µt = 2, and the number of technicians increases by 2, the probability of unwanted states decreases on puns = 0.49. So, the employment of new technicians has the greater influence on the decrease of puns than the increase of the technicians' intensity of processing the requests. The difference is significant: Δpuns = 0.74-0.62 = 0.12 when one technician is employed, while Δpuns = 0.74 - 0.49 = 0.25 when second technician is employed. The difference is significant and in this case the puns decrease when the second technician is em-ployed is more than twice the puns decrease when the intensity of technicians' processing the requests increases two times (puns decreases from 0.74 to 0.62, or Δpuns = 0.12 when pro-cessing intensity doubles, compared to the decrease from 0.74 to 0.49, or Δpuns = 0.25 when second technician is employed)
Conclusions
In this paper we presented the simulation model for the analysis of assistants' and technicians' engagement in the university teaching process. A specific feature of the system is that assistants have a dual role: they generate requests, but also process those requests, which can't be processed by technicians. The presented simulation model enables analysis of the complex systems behavior, when results cannot be obtained analytically. The model presented enables us to analyze the system in the cases when there are a lot of possible states of the system, when it is very difficult to obtain the results, which present the behavior of the system, using the mathematical analysis.
The main objective of the research presented in this paper, was the development of the simulation program for the analysis of assistants' and technicians' engagement in University teaching processes. This objective is fulfilled successfully, because the result of the developed simulation program for some simple systems agree with the results obtained analytically. The analysis of the results shows that it is desirable to devote all available technicians to all professors and assistants to process their requests. The total mean number of engaged assistants for the processing of the requests which cannot be processed by the technicians is smaller when all technicians can process the requests of all assistants and professors. At the same time, the mean number of engaged technicians is greater then (as technicians are utilized in a better way). This is illustrated in the paper by two numerical examples for small systems. These two systems differ in the number of employed technicians.
Besides this, in the simulation proved that better results in decreasing the probability of unwanted states (puns) is obtained by the employment of new technicians than by increasing the intensity of technicians' processing the requests. The difference between these two probabilities is illustrated by one numerical example for a small system. The results in this example are obtained both analytically and by simulation.
The simulation program proposed enables the analysis of significantly greater systems than the ones presented in this paper. Besides this, the program can be easily modified to analyze other similar queueing systems.
The results of this paper are especially important for the organization of auxiliary jobs in the faculty. It helps to decide how to distribute available technicians and whether to employ new technicians or to increase efficiency of technicians' engagement in the case of greater request volume.
The model in this paper supposes that an assistant who started processing requests, because there was no free technician, continues this action even when some technician finishes his instantaneous activity and becomes free. This is not the most suitable for the system. The more desirable arrangement is that a technician takes over request processing from the assistant as soon as he becomes free. The first future research direction is to implement such a processing scenario in the analysis.
The second research direction is to develop a model that considers the price needed to pay for processing generated requests by technicians and assistants. This model has to take into account not just the salaries, but also the penalties for the delay in the teaching process realization.
Concluding comment
The authors are willing to cede the simulation program to anyone who is interested.
References
Aizpun, M., Sandino, D., & Merideno, I. (2015). Developing students' aptitudes through University-Industry collaboration. Ingeniería e Investigación, 35(3), 121-128. DOI: 10.15446/ing.investig.v35n3.48188. [ Links ]
Bogoya, J. D., & Bogoya, J.M. (2013). An academic value-added mathematical model for higher education in Colombia. Ingeniería e Investigación, 33(2), 76-8. Retrieved from http://www.revistas.unal.edu.co/index.php/ingeinv/article/view/39521/41407#. [ Links ]
Filipowitz, B., & Kwiecien, J. (2008). Queueing systems and networks. Models and applications. Bulletin of the Polish Academy of Sciences, Technical Sciences, 56(4), 379-390. Retrieved from http://bluebox.ippt.pan.pl/~bulletin/(564)379.pdf. [ Links ]
Kleinrock, L. (1975). Queueing Systems. New York: John Wiley & Sons. [ Links ]
Kosten, K. M. (1970). Simulation in traffic theory. Proceedings of 6th ITC, Münich. [ Links ]
Kotnour, T. (1999). Developing and evaluating an organizational learning process to continuously improve teaching. IEEE Transactions on Education, 42(4). DOI: 10.1109/13.804561. [ Links ]
Lebl, A., & Mitic, D. (2014). Financial cost model of hiring technicians in teaching operations at the faculty. Proceedings of International Scientific Conference Management 2014, Union University Belgrade. Retrieved from http://www.meste.org/konf/Arhiva/Man_2014/PDF/068.pdf. [ Links ]
Macias, J. A. (2012). Enhancing Project-Based Learning in Software Engineering Lab Teaching Through an E-Portfolio Approach. IEEE Transactions on Education, 55(4), 502-507. DOI: 10.1109/TE.2012.2191787. [ Links ]
Mbarika, V. W., Sankar, C.S., & Raju, P.K. (2003). Identification of factors that lead to perceived learning improvements for female students. IEEE Transactions on Education, 46(1), 26- 36. DOI: 10.1109/TE.2002.804407. [ Links ]
Nikolic, S., Vial, P.J., Sankar, C.S., Ros, M., Stirling, D., & Ritz, C. (2015). Improving the Laboratory Learning Experience: A Process to Train and Manage Teaching Assistants. IEEE Transactions on Education, 58(2), 130-139. DOI: 10.1109/TE.2014.2335712. [ Links ]
Olsson, K.M. (1970). Simulation on computers. A method for determining the traffic-carrying capacities of telephone systems, TELE, XXII(1). [ Links ]
Pardede. E., & Lyons. J. (2012). Redesigning the assessment of an entrepreneurship course in an information technology degree program: Embedding assessment for learning practices. IEEE Transactions on Education, 55(4), 566-572. DOI: 10.1109/TE.2012.2199757. [ Links ]
Petrovic, G., Petrovic, N., & Marinkovic, Z. (2008). Application of the Markov Theory to Queueing Networks. Facta Universitatis, Series Mechanical Engineering, 6(1), UDC 519.217: 519.61, 45-56. Retrieved from http://facta.junis.ni.ac.rs/me/me2008/me2008-05.pdf. [ Links ]
Rodrigues, A., & De los Mozos, J.R. (1972). Roulette model for the simulation of delay-loss systems. ITT Electrical Communication, 47(2). [ Links ]
Siddiqi, R., Harrison, C. J., & Siddiqi, R. (2010). Improving Teaching and Learning through Automated Short-Answer Marking. IEEE Transactions on Learning Technologies, 3(3), 237-249. DOI: 10.1109/TLT.2010.4. [ Links ]
Šuh, T., Mitic, D., Lebl-Antonic, D., & Lebl, A. (2014). Determination of the Necessary Number of Technicians on the Faculty. Acta Polytechnica Hungarica, 11(1), 21-36. Retrieved from http://uni-obuda.hu/journal/Šuh_Mitic_Lebl-Antonic_Lebl_47.pdf. [ Links ]