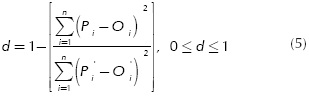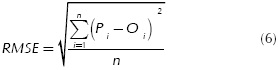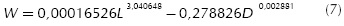Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.36 no.3 Bogotá Sep./Dec. 2016
https://doi.org/10.15446/ing.investig.v36n3.52336
DOI: http://dx.doi.org/10.15446/ing.investig.v36n3.52336
Growth model of the pineapple guava fruit as a function of thermal time and altitude
Modelo de crecimiento del fruto de feijoa en función del tiempo térmico y la altitud
Alfonso Parra-Coronado1, G. Fischer2, and J.H. Camacho-Tamayo3
1 Agricultural Engineer, Universidad Nacional de Colombia. MSc. Environmental Management, Pontifícia Universidad Javeriana, Colombia. Ph.D., Agricultural Sciences, Universidad Nacional de Colombia. Affiliation: Department of Civil and Agricultural Engineering, Universidad Nacional de Colombia, Bogotá, Colombia. E-mail: aparrac@unal.edu.co
2 Horticultural Engineer, Rhein-Main-Universität, Germany; MSc. Agr., Tech-nische Universität Berlin, Germany; Ph.D., Agricultural Sciences, Humboldt University Berlin, Germany. Affiliation: Agronomy Department, Universidad Nacional de Colombia, Bogotá, Colombia. E-mail: gfischer@unal.edu.co
3 Agricultural Engineer, Universidad Nacional de Colombia. MSc. Agricultural Engineering, Universidade Estadual de Campinas, Brasil. Ph.D., Agricultural Sciences, Universidad Nacional de Colombia. Affiliation: Department of Civil and Agricultural Engineering, Universidad Nacional de Colombia, Bogotá, Colombia. E-mail: jhcamachot@unal.edu.co
How to cite: Parra-Coronado, A., Fischer, G., & Camacho-Tamayo, J. H. (2016). Growth model of the pineapple guava fruit as a function of thermal time and altitude. Ingeniería e Investigation, 36(3), 06-14. DOI: 10.15446/ing.investig.v36n3.52336
ABSTRACT
The growth of the pineapple guava fruit is primarily stimulated by temperature but is also influenced by other climactic factors, such as altitude. The goal of this study was to develop a growth model for the pineapple guava fruit as a function of thermal time (GDD, growing-degree day) and altitude (H) of the production area. Twenty trees per farm were marked in two sites in the Cundinamarca region (Colombia) during the 2012 and 2014 seasons. Measurements were performed every seven days after day 96 and 99 post-anthesis until harvest in the sites of Tenjo (2580 m.a.s.l.) and San Francisco de Sales (1800 m.a.s.l.), respectively. A growth model was produced for weight as a function of fruit length and diameter as well as for the weight of the fruit as a function of GDD and H, with this last measure adjusted to a sigmoidal logistic growth model. The parameters for the regression analysis showed that the models satisfactorily predicted fruit growth for both of the sites, with a high determination coefficient. The cross-validation showed good statistical fit between the predicted and observed models; the intercept was not significantly different than zero, and the slope was statistically equal to one.
Keywords: Acca sellowiana, fruit weight, growing-degree days.
RESUMEN
El crecimiento del fruto de la feijoa es principalmente estimulado por la temperatura, pero también es afectado por otros factores climáticos como la altitud. El objetivo de este estudio es proponer un modelo de crecimiento del fruto de la feijoa en función del tiempo térmico (GDC, grados día de crecimiento) y de la altitud (H) de la zona de producción, para lo cual se marcaron veinte árboles por finca en dos localidades del departamento de Cundinamarca (Colombia), durante los años 2012 a 2014. Las mediciones se realizaron cada 7 días a partir del día 96 y 99 después de antesis hasta la cosecha, para las localidades de Tenjo (2580 m.s.n.m.) y San Francisco de Sales (1800 m.s.n.m.) respectivamente. Se obtuvo un modelo de crecimiento para el peso en función de la longitud y el diámetro del fruto, así como para el peso del fruto en función de GDC y H, ajustándose esta última a un modelo de crecimiento sigmoidal logístico. Los parámetros del análisis de regresión mostraron que los modelos predijeron satisfactoriamente el crecimiento del fruto para las dos localidades, con alto coeficiente de determinación. La validación cruzada mostró buen ajuste estadístico entre valores pronosticados y observados; la intercepción no fue significativamente diferente de cero y la pendiente fue estadísticamente igual a uno.
Palabras clave: Acca sellowiana, peso del fruto, grados-día de crecimiento.
Received: August 10th 2016 Accepted: November 21st 2016
Introduction
The feijoa fruit (Acca sellowiana (O. Berg) Burret), known in English-speaking countries as the pineapple guava, belongs to the order Myrtales, family Myrtaceae, subfamily Myrtoideae (Perea, Fischer & Miranda, 2010). The species is originally from South America, in areas spanning across Brazil, Uruguay, western Paraguay, and northeastern Argentina (Schuman & Ludders, 1992). Pineapple guava is a perennial and long-living species. Trees yield regularly once a year under seasonal subtropical conditions. However, in tropical areas, the species can produce continuously throughout the year (Quintero, 2012).
The pineapple guava is considered to be a promising crop for the Colombian Andean region, thanks to its excellent adaptation to areas between 1800 and 2700 m.a.s.l. There are several commercial varieties of pineapple guava fruit in Colombia (Clone 41 'Quimba', clone 8-4, Mammouth, Apollo, Gemini, Triumph, Rionegro, Tibasosa, among others). These are also considered to be important for pollination and for obtaining high-quality fruits (Parra & Fischer, 2013). For Colombia, Quintero (2012) estimated total pineapple guava production area to be 650 ha, with Boyacá, Cundinamarca, Santander, and Norte de Santander being the primary producing regions.
The fruit is defined as the primary sink in the context of photoassimilate competition (Link, 2000) and can be determined by a variety of factors such as phloem transport, compartmentalization, and metabolism (Ho, 1996). Final pineapple guava fruit weight and size differ greatly among cultivars as well as among fruits of the same cultivar (Vela, Salinero, Pinón & Sainz, 2009) and vary according to the position of the fruit in the canopy (Martínez-Vega, Fischer, Herrera, Chaves & Quintero, 2008). Size and weight are closely related to the physiological and phenological characteristics of the plant, growing conditions and prevailing environmental conditions during the fruit growth phase.
Growth refers to the irreversible increase in dry material or volume, changes in shape, size, mass, or number of structures, and is a function of the genotype and the environment (Krug, 1997), resulting in a quantitative increase in the size and weight of the plant or of an organ (Ardila, Fischer & Balaguera-López, 2011). Growth is a complex process including many processes such as cell division, elongation and enlargement, anabolism related to photosynthesis, synthesis of other compounds (e.g. amino acids, fatty acids, vitamins etc.) and these occur concurrent to catabolic processes such as respiration (Romani, 1984; Gómez, Ávila & Escalona, 1999). The study of growth is useful to determine the way in which the fruits increase in size and weight related to its age, until reaching the size and the weight at the time of the harvest (Coombe, 1976; Avanza, Bramardi, & Mazza, 2008), and the physiological maturity or optimal harvest state (Canizares, Laverde & Puesme, 2003), analyzing the formation and structural development of fruit over time (Mazorra, Quintana, Miranda, Fischer & Chaparro, 2006), and proposing a proper crop management (Rojas-Lara, Pérez-Grajales, Colinas-León, Sahagún-Castellanos & Avitia-García, 2008).
Growth can be quantified using models defined with mathematical expressions or functions that include a set of indexes (Hunt, 1990). A mathematical model helps synthesize and increase knowledge of a particular system (López, Ramírez & Rojano, 2005), evaluate possible management strategies, and make potential estimates of output, costs, and benefits of the use of specific commercial transactions and of the use of cultivation practices such as fertilization and irrigation (Canizares et al., 2003). Rates are determined by expressing the fruit-growth dynamics through measurements of dry or fresh material over determined time intervals (Ardila et al., 2011). The main intervals include the absolute growth rate (AGR), which indicates the change in size per unit of time, and the relative growth rate (RGR), which expresses the rate of variation in size per unit of initial weight (Hunt, 1990).
Among the nonlinear models used to characterize development and/or growth as a function of time, the logistic, the exponential, and the monomolecular models (Rojas-Lara et al., 2008; Ardila et al., 2011; Franco, 2013) as well as the Michaelis-Menten models (Rojas-Lara et al., 2008) stand out. The logistic model results from combining the exponential and the monomolecular model separated by a turning point, and is characterized by its sigmoidal shape (Rojas-Lara et al., 2008; Franco, 2013). The exponential model is valid for continual increases or decreases for which conditions are always favorable (Rojas-Lara et al., 2008). The monomolecular model indicates that the rate of change in dry weight of a plant is determined by the quantity of growth that remains to take place, which is why the growth rate shows a constant rate of decrease. The monomolecular model has been used to estimate the growth of different plant structures and pathogens (Franco, 2013).
Salisbury & Ross (2000) demonstrate that some fruits show a double-sigmoid growth behavior, such as raspberries, grapes, blackberries, olives, and stone fruit (e.g., peaches, cherries, and plums). Others show simple-sigmoid growth curves, as in the case of the passifloras (Gómez et al., 1999), apples, tomatoes, pears, oranges, pineapples, melons (Salisbury & Ross, 2000), avocados (Salisbury & Ross, 2000), and pineapple guava (Rodríguez, Arjona & Campos, 2006).
Often, calendar time has been used to predict growth and development stages in crops (Mendoza López, Luis Aguilar & Castillo Orta, 2004); however, a series of models have been proposed to improve the use of calendar time in predicting growth and development to describe the effect of temperature on phonological development (Warrington & Kanemasu, 1983). One of the most widely used methods is average daily temperature accumulation above a base temperature (Tb) (Monteith, 1984), known as thermal time, growing - or development - degree days (GDD), heat units (López, Chaves, Flórez & Salazar, 2010), or physiological time, and is defined as the quantity of degree days necessary to complete a particular development process or phonological phase (Trudgill, Honek & Van Straalen, 2005). Thermal time is used to calculate the appearance of nodes, leaves, and inflorescences, and to estimate the growth and development of fruits (Almanza, Quijano-Rico, Fischer, Chávez & Balaguera-López, 2010), as well as to estimate potential production (Salazar, Jones, Chaves & Cooman, 2008), among other factors.
There are various ways of calculating GDD, but the most common in agricultural and phonological studies is to calculate this parameter as the sum of the difference between average temperature and base temperature (Tb), with the average temperature calculated as the average of the minimum and maximum daily temperatures (Matzarakis, Ivanova, Balafoutis & Makrogiannis, 2007). The aforementioned calculation method to obtain GDD is well suited to describe growth and development because it is independent of environment or year (Ritchie & Ne Smith, 1991). One basic requirement for this focus is determining the critical temperature or base temperature (Tb), below which phonological development ceases or the plant discontinues its metabolic processes (Steinmaus, Prather & Holt, 2000). In the case of pineapple guava, the estimated base temperature for fruit growth is 1,76 °C (Parra-Coronado, Fischer & Chaves-Cordoba, 2015).
The aim of the present study was to evaluate the growth of the Quimba cv. pineapple guava in thermal time and to develop a physiological growth model for crops located at different altitudes.
Materials and methods
Location and characterization of study areas
The study was carried out on two farms. One, "La Pradera" farm, is located in the Tenjo municipality (4° 51' 23" N and 74° 6' 33" W) at 2580 m.a.s.l., with average annual temperature of 12,5 °C and relative humidity ranging from 74 % to 86 %; rainfall is bimodal, with annual average precipitation of 765 mm, concentrated between the March-May and September-November periods. The other one, "Mesopotamia" farm, is located in the San Francisco de Sales municipality (4° 57' 57" N and 74° 16' 27" W) at 1800 m.a.s.l., average annual temperature of 20,6 °C, and relative humidity ranging from 63 to 97 %; the rainfall is also bimodal, with annual average precipitation of 1493 mm, concentrated between February-May and September-November.
Pineapple guava trees over 16 years old (Clone 41 'Quimba') were grown with similar crop-management practices. Soil characteristics for both farms were sandy loam and similar ratios Ca / Mg, Mg / K, Ca / K and (Ca + Mg)/ K.
Experimental design
Because the pineapple guava is a perennial crop, 10 trees per individual plot and two places per farm were considered in this study, with a total of 40 trees included in the study (Fernández, Trapero & Dominguez, 2010). Thus, two blocks of information per harvest and farm were available, which allowed for additional information for validating the fruit growth model.
Trees were located in the middle of the growing lot, with the goal of maintaining uniformity in climactic conditions and eliminating border effects. Each whole tree plot (sample unit) was numbered, and the present flower buds in the middle third of the canopy were marked to follow fruit growth and development. Sampling was performed in 10 trees per plot, randomly selecting fruits from each tree once weekly after day 96 and 99 post-anthesis until harvest in the Tenjo and San Francisco de Sales sites, respectively. This procedure was performed over two consecutive years (halfway through 2012, 2013, and at the beginning of 2014) for two harvest periods. Due to the primary climatic conditions during the studied period, the evaluated plants only produced one harvest per year. The meteorological data were obtained from automatic meteorological stations iMETOS ECO D2 (Pessl Instruments, Weiz, Austria) that collect temperature, precipitation, relative humidity, and total radiation measurements each hour.
Thermal time (TT) in growing-degree days (GDD) was determined beginning with anthesis, using the Tb estimated by Parra-Coronado et al. (2015) for pineapple guava fruit growth of 1,76 °C. Thermal time was estimated as the daily sum of the difference between average temperature and base temperature for each stage (Equation (1)):
where TT is thermal time (GDD) accumulated over n days of fruit growth, Ti is the daily average temperature (°C) for the i-th day, and Tb is the base temperature (°C). GDDi for TT accumulation are calculated based on the following considerations:
where Tmax is the maximum temperature (°C) for the i-th day, and Tmin is the minimum temperature (°C) for the i-th day.
Growth variables measured in the study were (a) the variation in individual fresh weight of the fruit in grams, using the gravimetric method, and (b) the individual equatorial diameter and length of the fruit (mm) measured using a Vernier caliper. To evaluate fruit growth in each site as only a function of GDD, nonlinear polynomial, exponential, and sigmoidal models were first tested for fruit weight variation. The best-fitting equations were chosen based on those with the greatest determination coefficient (R2) and lowest standard error. Based on the best-fit equations for both of the sites, a specific growth model was chosen as a function of thermal time (GDD) and altitude (H) in the production zone, choosing the one with greatest R2 and lowest standard error. Likewise, an individual growth model was created for weight as a function of fruit length and diameter. The Solver for Excel® tool was used to estimate the parameters of these individual growth models. Solver is an iterative nonlinear procedure making the first estimate with initial values assigned to equation parameters and then increasing or decreasing the parameter values until a minimum value for the sum of the squared deviations is reached (Parra-Coronado et al., 2015).
The combined data average from two different periods for the cultivar and for each site studied (one parcel per crop) were used to develop the models. The sum of temperatures with corresponding Tb was averaged for each site. The entries for the growth model as a function of GDD and H included the anthesis date, the Tb value for fruit growth, the daily meteorological data including maximum and minimum temperatures (°C), and the altitude of the production area in each site.
Each of the equations obtained for evaluating the models were used on the remaining data. Cross-validation was performed between observed and simulated values, making it possible to visualize the quality of the model. The determination coefficient (R2), the matching index d (Equation (5)), and the root mean-square error RMSE (Equation (6)) were calculated to determine general model performance (Parra-Coronado et al., 2015). A descriptive statistical analysis was also performed using SPSS v.17 (SPSS Inc., Chicago, IL, USA),
where (n) is the number of observations, (Pi) is the predetermined value for the i-th date, and (Oi) is the observed value for the i-th date, P i = Pi - Ō, and O . = O . - Ō ; the general average for observeP va=ps is Ō .
where (n) is the number of observations, (Pi) is the predetermined value of the i-th date, and (Oi) is the observed value for the i-th date.
Results and discussion
The results obtained in this study show that pineapple guava fruit weight and size at harvest time are greater for fruits produced at higher altitude (2580 m.a.s.l.: fresh weight from 38,2 ± 4,2 to 98,9 ± 12,6 g, diameter from 35,2 ± 1,4 to 49,1 ± 2,5 mm; and 1800 m.a.s.l.: fresh weight from 30,5 ± 4,7 to 45,7 ± 6,8 g, diameter from 32,5 ± 2,6 to 40,0 ± 1,9 mm), requiring a greater number of calendar days and lower thermal time (GDD) to reach harvest from anthesis. Regina et al. (2010) found similar results for Chardonnay and Pinot Noir grapes cultivated in Minas Gerais State (Brazil), and indicated that the grapes cultivated at 1150 m.a.s.l. were larger and heavier than those grown at 873 m.a.s.l.
Individual pineapple guava fruit-weight equation as a function of length and diameter.
A well-fitting unique growth equation for pineapple guava fruit weight as a result of fruit diameter and length (Equation (7)) was obtained, with an R2 determination coefficient of 0,9984 and standard error of 0,695.
where W: fruit weight (g)
L: fruit length (mm)
D: fruit diameter (mm)
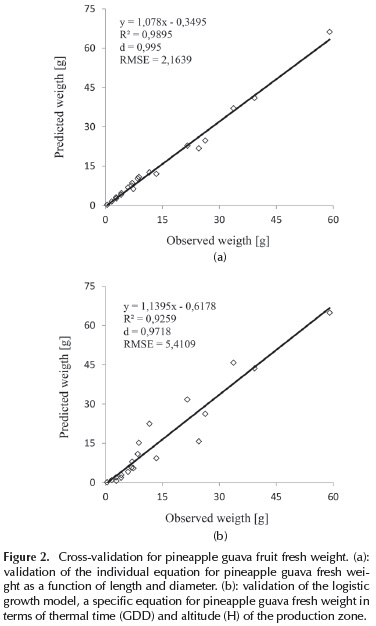
Figure 2a shows the cross-validated model evaluation using a comparison of predicted and observed weights during fruit growth. The cross-validation and regression analysis parameters showed that the model satisfactorily predicted pineapple guava fruit weight as a function of the fruit length and diameter. A good statistical agreement was found: the intercept was not significantly different from zero, and the slope was statistically equal to 1; these values are the expected estimates for a very strong goodness of fit between the predicted values (Y) and observed values (X). Moreover, the regression also showed a high determination coefficient (R2); the rate of matching (d) and the average root mean-square error (RMSE) also show a good fit in the model as a function of these dimensions for any of the production zones.
The model represented using Equation (7) can be applied to determine the weight of the fruit in any pineapple guava-production area in altitudes between 1800 and 2589 m.a.s.l. It is also possible to predict potential production from a determined site through the use of non-destructive measurements, such as the approximate determination of the number of fruits and the length and diameter of the fruit. Until now, there have been no equations that allow the determination of pineapple guava fruit size as a function of its dimensions for any production zone, and thus, the results of this study will help increase knowledge of the crop and improve its management to have greater production yields.
Mathematical models of thermal time for fruit weight
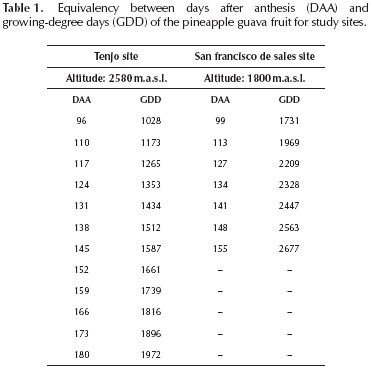
Table 1 shows the equivalency between days after anthesis (DAA) and thermal time or growing-degree days (GDD) for the pineapple guava fruit for the study areas; the fruit growth required 1972 GDD (180 DAA) to be harvested in the Tenjo site, while in San Francisco de Salas, the plants needed 2677 GDD (155 DAA). This result indicates that at higher altitudes, more calendar days are needed to arrive at harvest, but fewer GDD are needed because they depend directly on temperatures measured in each site.
The fruit weight as a function of GDD fit different types of growth curves (Table 2) for the fruit produced in two sites at the two extremes of production altitude (1800 m.a.s.l. for San Francisco de Salas and 2580 m.a.s.l. for Tenjo). Growth, represented by fruit weight, showed a good fit for polynomial (quadratic), exponential (simple with three parameters and Stirling Model), and sigmoid logistic nonlinear models. This finding agrees with those reported by Fischer (2003), Rodriguez et al. (2006), and Fischer, Ramírez & Almanza-Merchán (2012). The fruit growth curve had three post-anthesis stages: the first stage of slow growth lasted approximately 80 days after anthesis in both of the sites; stage two included faster growth from day 80 until day 127 (2209 GDD) for San Francisco de Sales, and from day 80 until day 145 (1587 GDD) for Tenjo; stage three, in which the fruit weight increased significantly in both of the sites, lasted from day 127 until harvest and from day 145 until harvest for San Francisco de Sales and Tenjo, respectively. These results coincide with those found by Rodriguez et al. (2006) for 'Quimba' pineapple guava and by Esemann-Quadros et al. (2008), who conducted feijoa fruit studies in anatomy and morphology.
Fischer (2003) showed that pineapple guava normally has a simple sigmoid growth curve (in size or weight) but can also express a double sigmoid depending on the cultivar and the agroecological conditions. Fruit development from anthesis until physiological maturity lasts from 120 to 150 days and is slow during the first 40 days. Rodriguez et al. (2006) observed that clone 41 (Quimba) and clone 8-4 fruit cultivated in the La Vega municipality (Cundinamarca), under similar climate conditions to San Francisco de Sales, showed a simple sigmoid growth curve, although the model that best described the fruit growth was the cubic polynomial one compared to quadratic and logistic models. These authors observed that the growth curve of the fruit showed three stages after anthesis: the first stage from 70 days post-anthesis was the slow-growing phase; the second stage lasted from day 70 until day 126, and the third stage lasted from day 126 until day 154. The authors also demonstrated that during the third development stage, the fruit volume increased significantly in both of the clones, which corroborated findings from Esemann-Quadros et al. (2008).
Several authors have used different models to describe the growth of certain fruit, including the following: Hernández & Martinez (1994) developed a quadratic model for the tamarillo fruit; González et al. (2001) used a polynomial model for star-fruit; Canizares et al. (2003) found a double sigmoidal growth model for guava fruit growth; Avanza et al. (2008) found the best model to describe the growth of 'Valencia late' sweet orange fruit to be a five-parameter logistic model; Almanza et al. (2010) found a logistic model fit for grape; Ardila et al. (2011) generated a sigmoidal logistic model for three tomato hybrids; and Silva, Silva, Matias, Ribeiro & Bruckner (2013) found a double sigmoid growth pattern for three peach genotypes. All of these models showed high R2 values, indicating their high predictive ability.
Specific mathematical model for fruit weight as a function of thermal time and altitude.
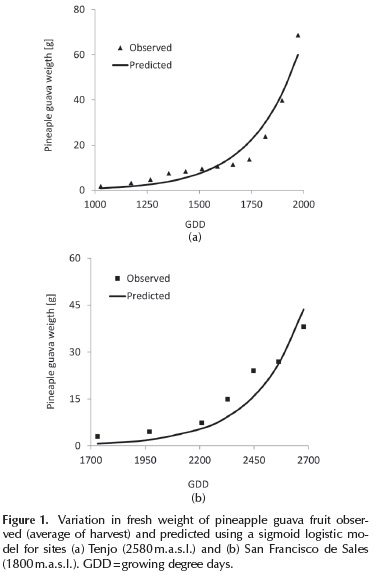
The best fit equations shown in Table 2 were modified by multiplying them with the factor (C*HD) to obtain a single equation for weight variation (W) for the pineapple guava in terms of thermal time and production area altitude; the H factor is the altitude (m.a.s.l.) of the production area, and C and D are parameters obtained by fitting the equation using the Solver® Excel toolkit. Table 3 shows equations obtained for pineapple guava fruit weight in terms of thermal time (GDD) and altitude (H); these equations were the only ones showing convergence when fit. Of the three equations found, the one showing the best fit was that belonging to the logistic sigmoid model, which showed a higher determination coefficient (R2 = 0,941) and lower standard error (3,830). Thus, this model is the best for predicting pineapple guava fruit weight as a function of GDD and H in production zones between 1800 and 2580 m.a.s.l. Figure 1 shows the observed and predicted weight variation in pineapple guava fruit using the logistic sigmoid model for the Tenjo and San Francisco de Sales sites.
The predicted fruit weight value at harvest time was underestimated by 14 % in the Tenjo site and overestimated by 12,5 % for the San Francisco de Sales site. This behavior is explained by the influence of the variation in other climactic factors on fruit growth in each of the evaluated harvests, such as solar radiation, rainfall, and moisture-retention characteristics of the soil (Fischer et al., 2012).
Figure 2b shows an evaluation of the model via cross-validation using a comparison of the predicted and observed weights during fruit growth (the remaining furrows not used for developing the model were used). The cross-validation and regression analysis parameters showed that the model satisfactorily predicted the weight of the pineapple guava fruit as a function of thermal time and production-area altitude. A good statistical agreement was found: the intercept was not significantly different from zero, and the slope was statistically equal to 1, which are the expected estimations for a very good fit between predicted values (Y) and observed values (X). Moreover, the regression showed a high determination coefficient (R2); the matching index (d) and root mean-square error (RMSE) also reflected a good fit of the model for fruit weight as a function of GDD and H for different production zones.
The sigmoidal logistic model equation shown in Table 3 can be used to determine fruit weight in any of the pineapple guava-production zones between the altitudes of 1800 and 2580 m.a.s.l. It is also possible to estimate potential production obtained in a given site by making approximate estimates of fruit numbers and keeping track of maximum and minimum temperatures in the site. Until now, there have been no equations allowing the determination of pineapple guava fruit weight in terms of thermal time and altitude of the production area, and thus, the results of this study are highly useful.
Additional evaluations of the model in different production zones are recommended, considering the influence of other factors in fruit development, such as cultivar and climate factors including radiation, rainfall, and moisture retained by the soil, accounting for climate variability and soil types that may exist in production zones.
Conclusions
The results found in this study show that the weight and size of pineapple guava fruits at harvest time have a direct relationship with the production zone altitude. Fruits produced at higher altitude required more calendar days and less thermal time (GDD) from anthesis to harvest. The regression analysis parameters showed that growth models for weight as a function of fruit length and diameter and for fruit weight as a function of thermal time and altitude satisfactorily predicted pineapple guava fruit growth for both of the sites with a high determination coefficient. A good statistical fit between predicted and observed values was found. Until now, there has been no model of this type that helped to determine pineapple guava weight as a function of related variables. This novelty makes the models found in this study of great value because they can be used to determine fruit weight in any pineapple guava-production zone, in similar latitudinal sites, between the altitudes of 1800 and 2580 m.a.s.l., as well as to estimate potential production in a particular site through non-destructive measures, such as the determination of fruit dimensions, production zone altitude, and GDD, as well as the approximate number of fruits under cultivation. We recommend to undertake further evaluations of these models for a wide range of pineapple guava varieties and environments.
Acknowledgments
We thank the Agricultural Sciences Faculty of the Universidad Nacional de Colombia, Bogota Campus, for providing financial support. We also thank Dr. Celsa Garcia Dominguez, professor in the Agronomy Department, and biologist Omar Camilo Quintero for providing valuable support, equipment, and the products necessary to conduct this study.
References
Almanza, P., Quijano-Rico, M., Fischer, G., Chávez, B., & Balaguera-López. H.E. (2010). Physicochemical characterization during growth and development of grapevine (Vitis vinifera L.) fruits under high tropical conditions. Agronomia Colombiana 28,173-180. [ Links ]
Ardila, G., Fischer, G., & Balaguera-López, H.E. (2011). Caracterización del crecimiento del fruto y producción de tres híbridos de tomate (Solanum lycopersicum L.) en tiempo fisiológico bajo invernadero. Revista Colombiana de Ciencias Hortícolas 5, 44-56. DOI: 10.17584/rcch.2011v5i1.1252. [ Links ]
Avanza, M.M., Bramardi, S.J., & Mazza, S.M. (2008). Statistical models to describe the fruit growth pattern in sweet orange 'Valencia late'. Spanish Journal of Agricultural Research 6, 577-585. DOI: 10.5424/sjar/2008064-352. [ Links ]
Canizares, A., Laverde, D., & Puesme, R. (2003). Crecimiento y desarrollo del fruto de guayaba (Psidium guajava L.) en Santa Bárbara, Estado Monagas, Venezuela. Revista UDO Agrícola 3, 34-38. [ Links ]
Coombe, B.G. (1976). The development of fleshy fruits. Annual Review of Plant Physiology 27, 207-228. DOI: 10.1146/annurev.pp.27.060176.001231. [ Links ]
Esemann-Quadros, K., Mota, A.P., Barbante, G., Guerra, M.P., Ducroquet, J.P.H.J., & Pescador. R. (2008). Estudo anatômico do crescimento do fruto em Acca sellowiana Berg. Revista Brasileira de Fruticultura, 30, 296-302. DOI: 10.1590/S0100-29452008000200005. [ Links ]
Fernández, R., Trapero, A., & Dominguez, J. (2010). Experimentación en agricultura. Sevilla: Consejeria de Agricultura y Pesca, Servicio de Publicaciones y Divulgación. [ Links ]
Fischer, G. (2003). Ecofisiologia, crecimiento y desarrollo de la feijoa. In: Fischer, G., Miranda, D., Cayón, G., & Mazorra, M. (Eds.). Cultivo, poscosecha y exportación de la Feijoa (Acca sellowiana Berg) (pp. 9-26). Bogotá: Produmedios. [ Links ]
Fischer, G., Ramírez, F., & Almanza-Merchán, P.J. (2012). Inducción floral, floración y desarrollo del fruto. En: Fischer, G. (Ed.), Manual para el cultivo de frutales en el trópico (pp. 120-140). Bogotá: Produmedios. [ Links ]
Franco, G. (2013). Caracterización fisiológica del fruto de gulupa (Passiflora edulis Sims), en condiciones del Bosque Húmedo Montano Bajo de Colombia. (Tesis inédita de doctorado). Facultad de Ciencias Agrarias, Universidad Nacional de Colombia. Medellin, Colombia. [ Links ]
Gómez, P.K., Ávila, E., & Escalona, A. (1999). Curva de crecimiento, composición interna y efecto de dos temperaturas de almacenamiento sobre la pérdida de peso de frutos de parchita 'Maracuya' (Passiflora edulis f. flavicarpa Degener). Revista de la Facultad de Agronomía, 25, 125-137. [ Links ]
González, D.V., Hernández, M.S., Herrera, A., Barrera, J.A., Martinez, O., & Páez, D. (2001). Desarrollo del fruto e índices de cosecha de la carambola (Averrhoa carambola L.) producida en el piedemonte amazónico colombiano. Agronomía Colombiana, 18, 7-13. [ Links ]
Hernández, M.S., & Martinez, W.O. (1994). Cambios morfológicos del fruto de tomate de árbol (Cyphomandra betacea. var. Tamarillo). Revista Comalfi, 21, 7-13. [ Links ]
Ho, L.C. (1996). The mechanism of assimilate partitioning and carbohydrate compartmentation in fruit in relation to the quality and yield of tomato. Journal of Experimental Botany, 47, 1239-1243. DOI: 10.1093/jxb/47.Special_Issue.1239. [ Links ]
Hunt, R. (1990). Basic growth analysis. Plant growth analysis for beginners. Unwin Hyman, Boston. DOI: 10.1007/978-94-010-9117-6. [ Links ]
Krug, H. (1997). Enviromental influences on development growth and yield. In: Wien, H.C. (Ed.). The physiology of vegetable crops. (pp. 101-180) London: Cabi Publishing. [ Links ]
Link, H. (2000). Significance of flower and fruit thinning on fruit quality. Plant Growth Regulation, 31, 17-26. DOI: 10.1023/A:1006334110068. [ Links ]
López, I.L., Ramírez, A., & Rojano, A. (2005). Modelos matemáticos de hortalizas en invernadero: Trascendiendo la contemplación de la dinámica de cultivos. Revista Chapingo Serie Horticultura, 11, 257-267. [ Links ]
López, M.A., Chaves, B., Flórez, V.J., & Salazar, M.R. (2010). Modelo de aparición de nudos en clavel (Dianthus car-yophyllus L.) cv. Delphi cultivado en sustratos. Agronomía Colombiana, 28, 47-54. [ Links ]
Martinez-Vega, R.R., Fischer, G., Herrera, A., Chaves, B., & Quintero, O.C. (2008). Caracteristicas fisico-quimicas de frutos de feijoa influenciadas por la posición en el canopi. Revista Colombiana de Ciencieas Hortícolas, 2, 21-32 DOI: 10.17584/rcch.2008v2i1.1170. [ Links ]
Matzarakis, A., Ivanova, D., Balafoutis, C., & Makrogiannis, T. (2007). Climatology of growing degree days in Greece. Climate Research, 34, 233-240. DOI: 10.3354/cr00690. [ Links ]
Mazorra, M.F., Quintana, A.P., Miranda, D., Fischer, G., & Chaparro, M. (2006). Aspectos anatómicos de la formación y crecimiento del fruto de uchuva Physalis peruviana (Solanaceae). Acta Biológica Colombiana, 11, 69-81. [ Links ]
Mendoza, López, M.R., Luis, Aguilar, A., & Castillo, Orta, S.F. (2004). Guayaba (Psidium guajava L.) su cultivo en el oriente de Michoacan. (Folleto técnico No. 4). Uruapan, Michoacan: Centro de Investigaciones del Pacifico Centro. Campo experimental Uruapan. [ Links ]
Monteith, J.L. (1984). Consistency and convenience in the choice of units for agricultural science. Experimental Agriculture, 20, 117-125. DOI: 10.1017/s0014479700000946. [ Links ]
Parra-Coronado, A., Fischer, G., & Chaves-Cordoba, B. (2015). Tiempo térmico para estados fenológicos reproductivos de la feijoa (Acca sellowiana (O. Berg) Burret). Acta Biológica Colombiana, 20, 167-177. [ Links ]
Parra, A., & Fischer, G. (2013). Maduración y comportamiento poscosecha de la feijoa (Acca sellowiana (O. Berg) Burret). Una revisión. Revista Colombiana de Ciencias Hortícolas 7 (1), 98-110. DOI: 10.17584/rcch.2013v7i1.2039. [ Links ]
Perea, M., Fischer, G., & Miranda, D. (2010). Feijoa. Acca sellowiana Berg. In: Perea, M., Matallana, L.P., & Tirado, A. (Eds.). Biotecnología aplicada al mejoramiento de los cultivos de frutas tropicales (pp. 330-349). Bogotá: Editorial Universidad Nacional de Colombia. [ Links ]
Fischer, G., & Miranda, D. (2012). Manual para el Cultivo de Frutales en el Trópico. Produmedios, Bogotá, Colombia. 443 - 473. [ Links ]
Regina, M.A., Carmo, E.L., Fonseca, A.R., Purgatto, E., Shiga, T.M., Lajolo, F.M., Ribeiro, A.P., & Mota, R.V. (2010). Influência da altitude na qualidade das uvas 'Chardonnay' e 'Pinot Noir' em Minas Gerais. Revista Brasileira de Fruticultura, 32, 143-150. DOI: 10.1590/S0100-29452010005000023. [ Links ]
Ritchie, J.T., & Ne Smith, D.S. (1991). Temperature and crop development. pp. 5-29. In: Hanks, R.J., Ritchie, J.T. (Eds.). Modelling plant and soil systems. American Society of Agronomy, Madison, WI. DOI: 10.2134/agronmonogr31.c2. [ Links ]
Rodriguez, M., Arjona, H.E., & Campos, H.A. (2006). Caracterización fisicoquimica del crecimiento y desarrollo de los frutos de feijoa (Acca sellowiana Berg) en los clones 41 (Quimba) y 8-4. Agronomía Colombiana, 24, 54-61. [ Links ]
Rojas-Lara, P.C., Pérez-Grajales, M., Colinas-León, M.T.B., Sa-hagún-Castellanos, J., & Avitia-Garcia, E. (2008). Modelos matemáticos para estimar el crecimiento del fruto de chile manzano (Capsicum pubescens R y P). Revista Chapingo Serie Horticultura, 14, 289-294. DOI: 10.5154/r.rchsh.2007.08.041. [ Links ]
Romani, R. (1984). Respiration, ethylene, and homeostasis in an integrated view of post-harvest life. Canadian Journal of Botany, 62, 2950-2955. DOI: 10.1139/b84-394. [ Links ]
Salazar, M.R., Jones, J.W., Chaves, B., & Cooman, A. (2008). A model for the potential production and dry matter distribution of cape gooseberry (Physalis peruviana L.). Scientia Horticulturae, 115, 142-148. DOI: 10.1016/j.scienta.2007.08.015. [ Links ]
Salisbury, F.B., & Ross, C.W. (2000). Fisiología de las Plantas 3. Desarrollo de las plantas y fisiología ambiental. Spain, Paraninfo S.A.: Thompson Editores. [ Links ]
Schuman, M. & Ludders, P. (1992). Cultivation of feijoa: Possibilities and limits in Colombia. Erwerbsobstbau, 34, 110-112. [ Links ]
Silva, D.F.P., Silva, J.O.C.E., Matias, R.G.P., Ribeiro, M.R., & Bruckner, C.H. (2013). Curva de crescimento e padrão respiratorio de frutos de genótipos de pessegueiro em região de clima subtropical. Revista Brasileira de Fruticultura, 35, 642-649. DOI: 10.1590/S0100-29452013000200037. [ Links ]
Steinmaus, S.J., Prather, T.S., & Holt, J.S. (2000). Estimation of base temperatures for nine weed species. Journal of Experimental Botany, 51, 275-286. DOI: 10.1093/jexbot/51.343.275. [ Links ]
Trudgill, D.L., Honek, A., Li, D., & Van Straalen, N.M. (2005). Thermal time - Concepts and utility. Annals of Applied Biology 146, 1-14. DOI: 10.1111/j.1744-7348.2005.04088.x. [ Links ]
Vela, P., Salinero, C., Pinón, P., & Sainz, M.J. (2009). Caracteristicas del fruto de Acca sellowiana cultivada en Galicia. Retrieved from: http://www.efa-dip.org/comun/publicaciones/comunicaciones/2009/feijoa%20%28logrono%29.pdf (accessed April 2014). [ Links ]
Warrington, I.J., & Kanemasu, E.T. (1983). Corn growth response to temperature and photoperiod I. Seedling emergence, tassel initiation and anthesis. Agronomy Journal, 75, 749-754. [ Links ]