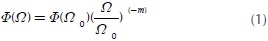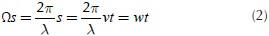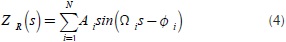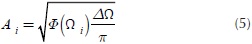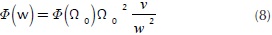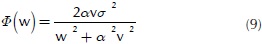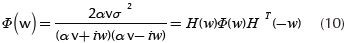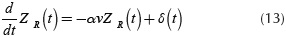Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.37 no.1 Bogotá Jan./Apr. 2017
https://doi.org/10.15446/ing.investig.v37n1.57277
DOI: http://dx.doi.org/10.15446/ing.investig.v37n1.57277
Evaluation of the methodologies used to generate random pavement profiles based on the power spectral density: an approach based on the International Roughness Index
Análisis de las metodologías utilizadas para generar perfiles aleatorios de pavimento con base en la densidad espectral de potencia (DEP): un enfoque ajuste basado en el Índice de Rugosidad Internacional
B. Goenaga1, L. Fuentes2, and O. Mora3
1 Boris Goenaga Silvera, MSc. Assistant Professor, Department of Civil and Environmental Engineering. Universidad del Norte Colombia. Barranquilla, Colombia. E-mail: bgoenaga@uninorte.edu.co
2 Luis Fuentes Pumarejo Ph. D. Chair, Department of Civil and Environmental Engineering, Universidad del Norte Colombia. Barranquilla, Colombia. E-mail: lfuentes@uninorte.edu.co
3 Otto Mora Civil Engineering. Research Assistant, Department of Civil and Environmental Engineering, Universidad del Norte Colombia. Barranquilla, Colombia. E-mail : olerma@uninorte.edu.co
How to cite: Goenaga, B. Fuentes, L. Mora, O. (2017). Evaluation of the methodologies used to generate random pavement profiles based on the power spectral density: An approach based on the International Roughness Index. Ingeniería e Investigación, 37(1), 49-57. DOI: 10.15446/ing.investig.v37n1.57277.
Received: May 3rd, 2016 Accepted: Jan 26th, 2017.
ABSTRACT
The pavement roughness is the main variable that produces the vertical excitation in vehicles. Pavement profiles are the main determinant of (i) discomfort perception on users and (ii) dynamic loads generated at the tire-pavement interface; hence its evaluation constitutes an essential step on a Pavement Management System. The present document evaluates two specific techniques used to simulate pavement profiles; these are the shaping filter and the sinusoidal approach, both based on the Power Spectral Density. Pavement roughness was evaluated using the International Roughness Index (IRI), which represents the most used index to characterize longitudinal road profiles. Appropriate parameters were defined in the simulation process to obtain pavement profiles with specific ranges of IRI values using both simulation techniques. The results suggest that using a sinusoidal approach one can generate random profiles with IRI values that are representative of different road types; therefore, one could generate a profile for a paved or an unpaved road, representing all the proposed categories defined by ISO 8608 standard. On the other hand, to obtain similar results using the shaping filter approximation, a modification in the simulation parameters is necessary. The new proposed values allow one to generate pavement profiles with high levels of roughness, covering a wider range of surface types. Finally, the results of the current investigation could be used to further improve our understanding on the effect of pavement roughness on tire pavement interaction. The evaluated methodologies could be used to generate random profiles with specific levels of roughness to assess its effect on dynamic loads generated at the tire-pavement interface and user's perception of road condition.
Keywords: Random process, power spectral pensity, sinusoidal approximation, shaping filter, pavement profile, roughness.
RESUMEN
La rugosidad del pavimento es la principal variable que produce la excitación vertical en los vehículos. Los perfiles de pavimento son los principales responsables de (i) la incomodidad percibida por los usuarios y, (ii) las cargas dinámicas generadas en la interfaz entre el neumático y el pavimento, de ahí que su evaluación constituye un paso esencial en un Sistema de Gestión de Pavimentos. El presente documento evalúa dos técnicas específicas utilizadas para simular perfiles de pavimento; estos son los filtros de forma y la aproximación sinusoidal, ambos basados en la Densidad de Potencia Espectral. La rugosidad del pavimento se evaluó utilizando el Indice Rugosidad Internacional (IRI), el cual es el índice más utilizado para caracterizar rugosidad del perfil longitudinal de una vía. En la presente investigación se definieron parámetros apropiados en el proceso de simulación para obtener perfiles de pavimento con rangos específicos de los valores de IRI utilizando ambas técnicas de simulación. Los resultados sugieren que el uso de la aproximación sinusoidal puede generar perfiles aleatorios con valores de IRI que son representativos de diferentes tipos de vías, por lo tanto, se podría generar un perfil para un pavimento nuevo o una vía sin pavimentar, cubriendo todas las categorías definidas por la norma ISO 8608. Por otro lado, para obtener resultados similares usando la metodología de filtro de conformación, es necesaria una modificación en los parámetros de simulación. Los nuevos valores propuestos permiten generar perfiles de pavimento con altos niveles de rugosidad, que cubren una gama más amplia de tipos de superficie. Por último, los resultados de la presente investigación se podrían utilizar para enriquecer lo que se conoce sobre el efecto de la rugosidad del pavimento en la interacción del pavimento de neumáticos. Las metodologías analizadas se podrían utilizar para generar perfiles aleatorios con niveles específicos de rugosidad (IRI) para evaluar su efecto sobre las cargas dinámicas generadas en la interfaz neumático-pavimento y la percepción del usuario del estado de la carretera.
Palabras Clave: Proceso aleatorio, densidad de potencia espectral, aproximación sinusoidal, filtro de forma, perfil del pavimento, rugosidad.
Introduction
Pavement roughness is the main variable that produces vertical excitation on vehicles. In absence of surface irregularities, any vertical acceleration experienced by a vehicle is generated by engine vibration, tire imbalance and other deterministic source of vibration (Kim, Rhee, Park, & Yun, 2009 and Reza-Kashyzadeh, Ostad-Ahmad-Ghorabi, & Arghavan, 2014). Thus, a significant effort has been dedicated to characterize the irregularities presented in a road pavement profile (Sayers, Gillespie, & Paterson, 1986). A detailed longitudinal pavement profile provides information associated with surface roughness and texture, as classified by the International Standardization Organization, (ISO 8608, 2016). This classification is based on the Power Spectral Density -PSD of the profile. Road profiles can be represented using a PSD function. To determine the Power Spectral Density function, or PSD, it is necessary to measure the surface profile with respect to a reference plane. Understanding pavement profiles represents a fundamental task considering that roughness has become one the most important and frequently used parameter in the decision-making process of Pavement Management Systems (PMS) (Flintsch, Zaniewski, & Delton, 1997 and Wang, Way, Delton, & Zaniewski, 1993).
The International Roughness Index (IRI) constitutes the roughness index most commonly used to characterize longitudinal road profiles. The IRI was initially proposed by the World Bank in 1986 to assess the perception of users on the condition of pavement surfaces.
Considering that pavement profiles are the main determinant of (i) discomfort perception on users and, (ii) dynamic loads generated at the tire-pavement interface, it is very important to understand its properties.
In the literature one can find two specific techniques used to simulate pavement profiles; these are the shaping filter (Schiehlen, 2006 and Tyan, Hong, Tu, & Jeng, 2009) and the sinusoidal approach (L. Sun, 2002), both of these based on the PSD.
Using these methodologies one can generate pavement profiles with different roughness levels. The present investigation aims to define appropriate parameters in the simulation process to obtain pavement profiles with specific ranges of IRI values. The results of the current investigation can be further used to study the effect of pavement roughness on the dynamic loads generated at the tire-pavement interface.
This document is organized as follow. Section II presents the methodology used to classify pavement profiles according to the PSD. Section III presents the sinusoidal and shaping filter methodologies for random profiles generation. Then, section IV presents the random profiles generated through the methodologies described in Section III. The IRI was calculated for each profile generated using the proposed methodologies and the results are presented in Section V. Finally, the main conclusions derived from this work are presented.
Pavement profile classification
Through the years, pavement profiles have been used to characterize the irregularities presented in a road. These irregularities are commonly summarized by a roughness index, and it have been found that roughness is one of the main variable that affect the tire-pavement interaction (Imine, Delanne, & M'Sirdi, 2006). The International Organization for Standardization (ISO 8608, 2016) proposes a methodology for classifying roads profiles based on the Power Spectral Density (PSD). The PSD allows representing a pavement as the sum of waves of different wavelengths and amplitudes, which are added one to the other by a mathematical transformation called the Fourier transform (Dodds & Robson, 1973 and Rill, 2006, 2012).
To determine the PSD of a pavement, it is necessary to measure the surface profile with respect to a reference plane. Random pavement profiles can be approximated by a PSD in the form of Equation (1) (Schiehlen, 2006; L. Sun, 2002 and Tyan et al., 2009).
where 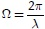 in rad/m is the spatial angular frequency, λ is the wavelength. Φ0∼Φ(Ω0) in m2/(rad/m) is the PSD value at a reference wave number Ω0=1 rad / m, and m is a pavement waviness indicator. It has been found that this parameter takes values of 1,75 < m<2,25, hence using m=2 is considered as a good estimate, (Schiehlen, 2006). It is important to note that the PSD presents a characteristic drop when the pavement wave number decreases (Andren, 2006 and Marcondes, Burgess, Harichandran, & Snyder, 1991).
in rad/m is the spatial angular frequency, λ is the wavelength. Φ0∼Φ(Ω0) in m2/(rad/m) is the PSD value at a reference wave number Ω0=1 rad / m, and m is a pavement waviness indicator. It has been found that this parameter takes values of 1,75 < m<2,25, hence using m=2 is considered as a good estimate, (Schiehlen, 2006). It is important to note that the PSD presents a characteristic drop when the pavement wave number decreases (Andren, 2006 and Marcondes, Burgess, Harichandran, & Snyder, 1991).
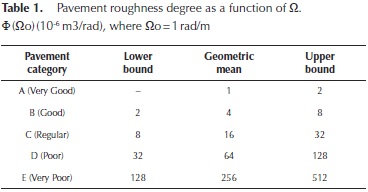
Table 1 presents the values of Φ(Ω0) suggested by the ISO 8608 to characterize pavement roughness of any kind of road. For a quick and proper estimation of the category of a given pavement profile, the ISO presents the following recommendations:
- New pavement surfaces such as flexible pavements could be assumed to have a good category. Category A and B.
- An old pavement layer that has not received any maintenance could be classified as an acceptable category. Category C.
- Unpaved low volume roads consisting of coarse aggregate surface or similar materials may be classified on a regular, poor or very poor roughness category. Category C through E.
Pavement profile in the time-frequency domain: The excitation on a vehicle tire is mainly conditioned by two factors, pavement roughness and vehicle velocity v (Cebon, 1999; Cole & Cebon, 1989 and Kavanagh & Ramanatan, 1982). Let s be the distance traveled, by definition the wavelength may be writing as 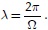 Assuming an initial condition of s=0 when t=0, the term Ωs may be written as,
Assuming an initial condition of s=0 when t=0, the term Ωs may be written as,
Where w is the angular velocity in the time domain in rad/ sec. Equation (2) can be rewritten to obtain Equation (3) as follows:
Hence the excitation frequency in the time domain is given by 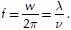 For most of vehicles the vibrations occur due to pavement profiles with waves which satisfy the conditions
For most of vehicles the vibrations occur due to pavement profiles with waves which satisfy the conditions 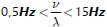 (Rill, 2006). Thus, to reach an excitation in the whole frequency range described above at a given vehicle speed, one needs to use different pavement wavelengths.
(Rill, 2006). Thus, to reach an excitation in the whole frequency range described above at a given vehicle speed, one needs to use different pavement wavelengths.
Random profiles estimation
Sinusoidal approximation
Longitudinal pavement profiles corresponding to a wheel track can be mathematically constructed from a set of sinusoidal waves with different wavelengths, amplitudes and phases. Assuming a vehicle travels at a constant speed over a road segment with length L, a random pavement profile is approximated overlaying an infinite number of sine waves 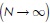 as described in Equation (4).
as described in Equation (4).
Where Ai is defined as follows,
As i=1,...,N where 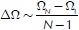 (rad/m), and the phase angles Φi are treated as a random variable, which follow a uniform distribution in the interval [0,2 π), (L. Sun, 2002; Tyan et al., 2009).
(rad/m), and the phase angles Φi are treated as a random variable, which follow a uniform distribution in the interval [0,2 π), (L. Sun, 2002; Tyan et al., 2009).
Shaping filter approach
The mean squared value of road surface roughness, that is the total area of the Power Spectral Density function, does not change with the velocity of a vehicle (Andren, 2006; Marcondes et al., 1991; B. L. Sun & Deng, 1998). Let Φ(w) denote the PSD that represents the excitation frequency induced by a road pavement profile, therefore we have the following relation:
Equation (3) could be used to rewrite Equation (6) as follows:
It can be shown that using Equations (1) and (3), with m=2, Equation (7) can be derived.
The above expression shows that pavement profile could be obtained from integrating a white noise process in the time domain. To avoid an increment on the standard deviation during the integration period, the PSD defined in Equation (8) must be modified to the next expression.
Where σ2 is the pavement profile variance, v is the vehicle velocity, while a is a constant that depends on the type of pavement surface, it is recommended to use following a values (Dharankar, Hada, & Chandel, 2016; Tyan et al., 2009).
- α=0,15 m-1 Corresponding to asphalt concrete roads.
- α=0,45 m-1 Corresponding to a paved road.
Where the term H(w)∼ 1/(αv+iw) corresponds to the frequency response function of the shaping filter process induced by the white noise with a PSD =2αvσ2. The pavement roughness variance may be obtained simplifying the expression given by the ISO 8608, and this may be approximated as follows;
However, the most used expression in the literature to define pavement roughness variance is defined as follow (ISO 8608) (Karnopp & Redfield, 1988)(Buhari, Zulkarnaini, Rohani, & Sulong, 2014).
Hence, if a vehicle travels over a pavement profile at a constant speed 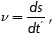 a pavement profile
a pavement profile 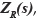 PSD defined by Equation (9), can be obtained from the output of a differential equation problem that is described by the Equation (13).
PSD defined by Equation (9), can be obtained from the output of a differential equation problem that is described by the Equation (13).
Where δ(t) is a white random process with a PSD as 2αvσ2 (Schiehlen, 2006). Replacing the expression given in Equation (12) in Equation (9) and solving to α with Ω = Ω0 an average value of α=0,117 m-1 is obtained, which is independent of the road category. Figure 1 shows the solution process scheme of Equation (13) that represents the shaping filter process, this problem has as input the white noise process with zero mean and variance that depends on the road category like was expressed in Equation (12). Finally, the differential equation is solved in a defined time interval, obtaining the pavement random profile as the system response.
Generation of pavement random profiles
100 profiles were generated for each category defined by the ISO 8608 for both shaping filter and sinusoidal approximation, for a total of 500 profiles for each method. The categories defined by the ISO 8608 can be found in Table 1.
Random profile generation using the sinusoidal approximation
Each random profile was generated using at least 1000 waves that included a large range of wavenumbers and amplitudes. The amplitude for each wave was defined using Equation (5). A total of 100 profiles were generated for each category described in Table 1. Figure 2 presents examples of random profiles generated to obtain specific roughness levels. Figure 2(a) shows a smooth random profile obtained using a set Φ (Ω0) = 1 x 10-6m3 / rad, while Figure 2(b) illustrates a rough random profile obtained using a set Φ (Ω0) = 256 x 10-6m3 / rad. A similar approach was used to generate the remaining profiles for each category.
Random profiles generation using a shaping filter approach
Simulink of Matlab can be used to solve the process described by Equation (13) to generate pavement random profiles, the entry of the process is the standard deviation of the white noise process which depends of the pavement category, a 80km/h∼22,2m/s speed and a value of α = 0,127m1 are set. The Equation (13) is analyzed in time intervals of 0.005 seconds, for a total period of 10 seconds, which allows collecting near of 2000 points of a pavement profile, representing a distance of 222 meters.
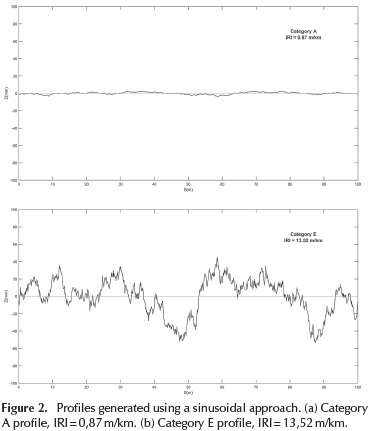
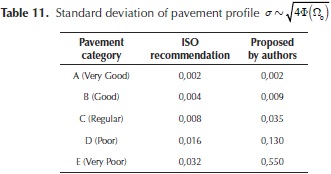
Table 2 presents the standard deviation values (σ) obtained using Equation (12) for the Φ(Ω0) values defined by the ISO 8608 for each pavement category.
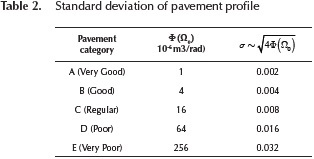
Figure 3 presents pavement profiles generated for category A with σ=0,002 and category E with σ=0,032. Again, a similar approach was used to generate the remaining profiles for each category.
Analysis of pavement random profiles based on IRI values
Power spectral density is a probabilistic method, which constitutes a measure of the mean squared value of a random variable. In general, this method is used for random vibration analysis, which describes how the power of a signal or time series is distributed over different frequencies. If one considers the pavement as a continuous surface, the IRI sequence of road profiles is a random phenomenon that obeys a zero-mean Gaussian distribution. This can be regarded as a stationary stochastic process (Du, Liu, Wu, & Jiang, 2014). Therefore, the IRI calculated from a random profile can also be considered as a random variable.
The random pavement profiles generated will be used to simulate the tire-pavement interaction for a specific road category (Table 1), therefore, it is necessary that these profiles that are used as an input of the quarter car model represents the roughness characteristic of each road category, where the roughness is represented by the International Roughness Index (IRI).
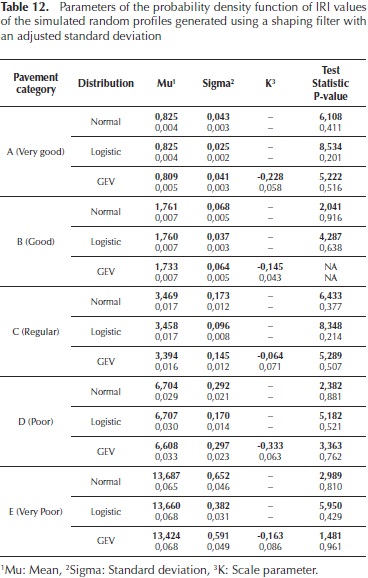
The IRI was calculated for each profile generated using the proposed methodologies in accordance to the ASTM E 1926. Furthermore, a statistical analysis was performed on the IRI values calculated on the different profiles for each category. The analysis included the determination of the probability density function that represents the variability of IRI for each category.
Analysis of IRIs from sinusoidal profiles
The histogram was developed to visually evaluate the IRI values obtained for each pavement condition category. In addition, an analysis was undertaken assessing whether a given distribution was suited to the IRI data-set for each category of pavement condition. The Statistics Toolbox of Matlab was used to evaluate the goodness of fit for the Normal, Logistic and Generalized Extreme Value (GEV) probability density functions.
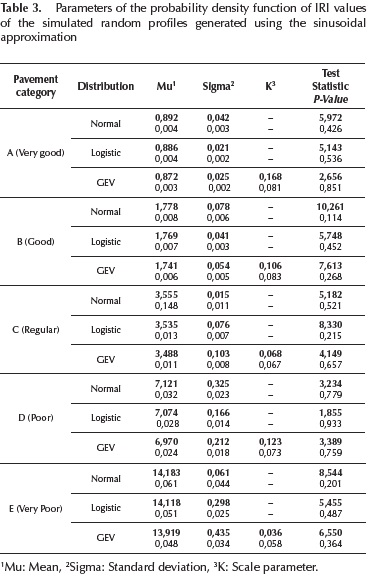
Table 3 presents the parameters of the probability density functions adjusted to the IRI values of each pavement category calculated on the random pavement profiles generated using the sinusoidal approximation.
The critical value for evaluating the null hypothesis H0 for each probability density function was 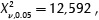 with a significance level of 0,05 and v degrees of freedom, where v=k - 1, and k representing the number of classes generated to calculate the frequency histogram. The class number generated in all cases was of 7. It can be statistically assumed that the function provides a proper data fit if
with a significance level of 0,05 and v degrees of freedom, where v=k - 1, and k representing the number of classes generated to calculate the frequency histogram. The class number generated in all cases was of 7. It can be statistically assumed that the function provides a proper data fit if 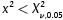 (p-value > 0,05). The results presented on Table 3 suggest that all the distributions evaluated provide a good fit, therefore, to choose the best function one could use the standard error of each parameter and the p-value of each probability function as selection criteria.
(p-value > 0,05). The results presented on Table 3 suggest that all the distributions evaluated provide a good fit, therefore, to choose the best function one could use the standard error of each parameter and the p-value of each probability function as selection criteria.
Analysis of IRIs from shaping filter profiles
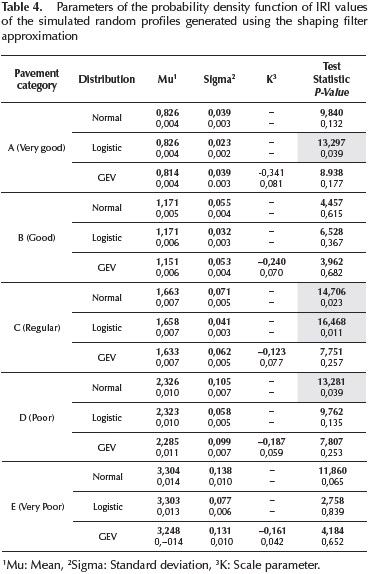
The same analysis was performed on the random pavement profiles generated using the shaping filter approximation. Table 4 details the fitting results for the three probability density functions; again the critical value for evaluating the null hypothesis H0 was 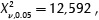
Table 4 shows that the only distribution that provides a good fit for all pavement categories is the Generalized Extreme Value function (GEV). The expected IRI values obtained for the categories A, B, C, D and E using the GEV were 0,814 m/km, 1,151 m/km, 1,633 m/km, 2,285 m/km y 3,248 m/km, respectively.
Discussion of results
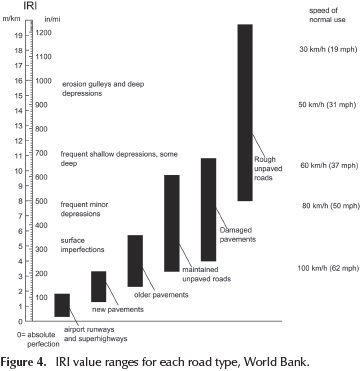
From the results presented above, one can conclude that random profiles generated using a sinusoidal approach present IRI values that are representative of a large variety of road types, from paved roads (Category A and B) with mean IRI values of 0,18 m/km and 1,8 m/km, to unpaved roads (Category E) with expected IRI values of 14,1 m/km. These results are consistent with the IRI specifications provided by the World Bank for different road types (Sayers et al., 1986), as shown in Figure 4.
On the other hand, the IRI values calculated on the profiles generated using the shaping filter approximation (Table 4) correspond to values representative of new roads, highways and airport pavements, just as it can be seen in Figure 4. As an example, Table 4 shows that a mean IRI value of 3,3 m/ km is associated to a pavement with a very poor condition (category E). These results suggest that the shaping filter methodology is only applicable to simulate pavement profiles for highways and road surfaces with high quality construction and maintenance standards.
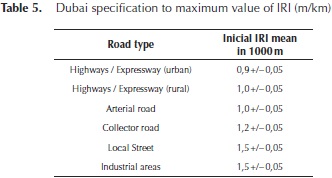
Tables 5-10 present typical technical specifications used by agencies around the world to assess road condition based on IRI values. For example, Table 5 presents the maximum initial IRI values allowed for different road types in Dubai.
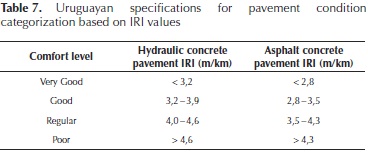
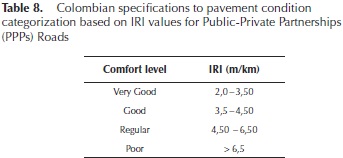
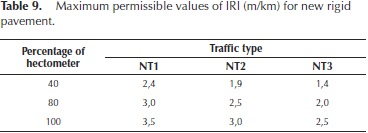
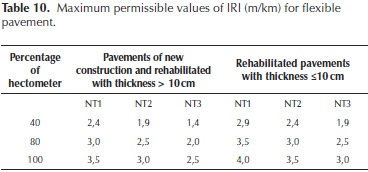
Table 6 shows the Canadian IRI specification to control the quality of the road network; the initial value for a new pavement cannot be greater than 1,8 m/km in one complete section of 100 meters. Table 7 presents the Uruguayan case which makes a distinction between asphalt concrete and hydraulic concrete pavement, establishing that maximum IRI values cannot be greater to 2,8 m/km. It is seen that the specification is more permissible with hydraulic concrete pavements. Table 8 presents the general specification used to manage the Public-Private Partnerships (PPPs) roads in Colombia, indicating that new roads or roads in good condition must present an IRI in the range of 2,0 m/km to 3,5 m/km. In addition, Table 9 presents the maximum permissible values of IRI for new rigid pavement for general highways in Colombia, this value depends on the traffic type, which is categorized by the Equivalent Single Axial Load (ESAL), where NT1 : ESAL's < 0,5 x 106, NT2 : ESAL's 0,5 x 106 to 5 x 106 and NT3 : ESAL's > 5 x 106, the range of IRI in this case is 1,4 m/km to 3,5 m/km. Table 10 presents the maximum permissible values of IRI for new or rehabilitated flexible pavement for general highways in Colombia, the range of IRI is 1,4 m/km to 4,0 m/km.
Summarizing, the IRI values accepted for new roads, highways or airport pavements in most cases are in the range of 1,0 m / km and 3,5 m / km, suggesting that the shaping filter methodology is the only applicable for this type of surfaces. However, the shaping filter approximation could be used to simulate a pavement random profile of any type of road with an appropriate calibration of the standard deviation of the white noise process.
Standard deviation recommended to generatea pavement random profile using a shaping filter approach
The standard deviation values presented in Table 2, which are recommended by ISO to generate random pavement profiles using a shaping filter approach, must be adjusted so that this methodology could be used to generate profiles with high IRI values. Therefore, the standard deviation of the white noise on the shaping filter process was adjusted to generate pavement random profiles consistent with the sinusoidal approach results.
Table 11 presents the proposed standard deviation values that could be used to generate pavement random profiles using a shaping filter approach with results consistent with the sinusoidal approximation. Table 12 shows the statistical analysis of the obtained IRI values, it can be appreciated that the mean values for each category are consistent with Figure 4 and the sinusoidal approach results.
Conclusions
Pavement profiles constitute a fundamental input on investigations directed to understand tire pavement interaction. An appropriate analysis of a profile would allow one to evaluate the dynamic forces developed at the tire-pavement interface due to roughness. In this paper, two of the most commonly techniques used to generate random pavement profile have been analyzed, the authors made a comparison between the results of the shaping filter and the sinusoidal approach which were obtained for each of the pavement categories defined in the ISO 8608.
500 profiles were generated using both methods. Specifically, 100 profiles were generated for each category for both shaping filter and sinusoidal approximation. The International Roughness Index (IRI) was calculated for each profile in accordance to the ASTM E 1926.
The results suggest that sinusoidal approach can be used to generate random pavement profiles with IRI values that being representative of different road types, this is, one can model profiles for a paved or an unpaved road in any of the categories defined by the ISO 8608. On the other hand, to obtain similar results using the shaping filter approximation a modification in the simulation parameters is necessary. An adjustment to the standard deviation values of the white noise process suggested by the ISO 8608 is proposed. The new proposed values allow one to generate pavement profiles with high levels of roughness, covering a wider range of surface types.
Finally, the results of the current investigation could be used to further improve understanding the effect of pavement roughness on tire pavement interaction. The evaluated methodologies could be used to generate random profiles with specific levels of roughness to assess its effect on dynamic loads generated at the tire-pavement interface and user's perception of road condition. The random profile would serve as an input to the quarter car model used to evaluate tire pavement interaction. In addition, the proposed probability density functions to characterize the IRI values could facilitate future simulation processes using techniques such as the Monte Carlo method. These density functions could be used to characterize IRI values obtained from random profiles defined to a specific roughness level.
Acknowledgment
The authors express their gratitude to the Gobernación del Atlántico and the National Government, for being partially fund-ed this work through the project LOGPORT BPIN 20120001001911050672 (Agreement No.0103-2013-000016).
References
Andren, P. (2005). Power spectral density approximations of longitudinal road profiles. International Journal of Vehicle Design, 40(1-3), 2-14. [ Links ]
Buhari, R., Zulkarnaini, M. R., Rohani, M. M., & Sulong, N. F. (2015). Longitudinal Road Profile Model Generation Based on Measurement Data Using Mathematical Approach. Advanced Science Letters, 21(12), 3627-3631. [ Links ]
Cebon, D. (1999). Handbook of vehicle-road interaction. Taylor & Francis. [ Links ]
Cole, D. J., & Cebon, D. (1989). Simulation and measurement of dynamic tyre forces. Cambridge University Press. [ Links ]
Delton, J. (1997). Expert project recommendation procedure for ADOT's pavement management system. (Doctoral dissertation, Arizona State University). [ Links ]
Dharankar, C. S., Hada, M. K., & Chandel, S. (2016). Numerical generation of road profile through spectral description for simulation of vehicle suspension. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 1-11. [ Links ]
Dodds, C. J., & Robson, J. D. (1973). The description of road surface roughness. Journal of sound and vibration, 31(2), 175-183. [ Links ]
Du, Y., Liu, C., Wu, D., & Jiang, S. (2014). Measurement of International Roughness Index by Using-Axis Accelerometers and GPS. Mathematical Problems in Engineering, 2014. [ Links ]
Imine, H., Delanne, Y., & M'sirdi, N. K. (2006). Road profile input estimation in vehicle dynamics simulation. 285-303: Vehicle System Dynamics, 44(4). [ Links ]
ISO 8608. (2016). Mechanical Vibrations - Road Surface Profiles - Reported Of Measured Data, ISO 8608: 2016. International Organization For Standardization. [ Links ]
Kavanagh, R. J., & Ramanathan, R. (1982). Computer simulation of road surface profiles for a four-wheeled vehicle. In Proceedings of the 14th conference on Winter Simulation-Volume 1 (pp. 337-346). Winter Simulation Conference. [ Links ]
Kim, S. M., Rhee, S. K., Park, H. B., & Yun, D. J. (2009). Correlations among Pavement Surface Roughness, Moving Dynamic Vehicle Loads, and Concrete Pavement Performance. In Performance Modeling and Evaluation of Pavement Systems and Materials: Selected Papers from the 2009 GeoHunan International Conference (pp. 25-31). [ Links ]
Marcondes, J., Burgess, G. J., Harichandran, R., & Snyder, M. B. (1991). Spectral analysis of highway pavement roughness. Journal of Transportation engineering, 117(5), 540-549. [ Links ]
Redfield, R. C., & Karnopp, D. C. (1988). Roadway elevation profile generation for vehicle simulation. Vehicle System Dynamics, 17(5), 267-280. [ Links ]
Reza-Kashyzadeh, K., Ostad-Ahmad-Ghorabi, M. J., & Arghavan, A. (2014). Investigating the effect of road roughness on automotive component. Engineering Failure Analysis, 41, 96-107. [ Links ]
Rill, G. (2008). Vehicle Dynamics, Lecture Notes. Regensburg: University of Applied Sciencies. [ Links ]
Rill, G. (2011). Road Vehicle Dynamics: Fundamentals and Modeling. Regensburg: University of Applied Sciencies. [ Links ]
Sawyers, M. W., Gillespie, T. D., & Paterson, W. D. (1986). Guidelines for Conducting and Calibrating Road Roughness Measurements. (No. Technical Paper 46). [ Links ]
Schiehlen, W. (2006). White Noise Excitation of Vehicule Structure. Sadhana, 31(4), 487-503. [ Links ]
Sun, L. (2003). Simulation of pavement roughness and IRI based on power spectral density. Mathematics and computers in simulation, 61(2), 77-88. [ Links ]
Sun, L., & Deng, X. (1993). Predicting vertical dynamic loads caused by vehicle-pavement interaction. Journal of transportation engineering, 124(5), 470-478. [ Links ]
Tyan, F., Hong, Y. F., Tu, S. H., & Jeng, W. S. (2009). Generation of Random Road Profile. Journal of Advanced Engineering, 4(2), 1373-1378. [ Links ]
Wang, K. C., Way, G., Delton, J., & Zaniewski, J. (1993). Pavement network optimization and implementation. Arizona. [ Links ]