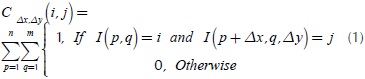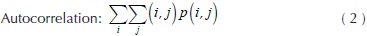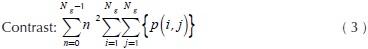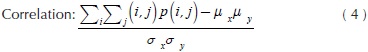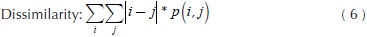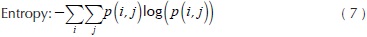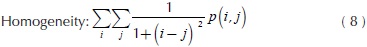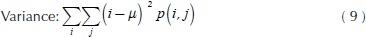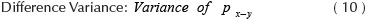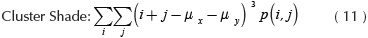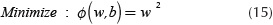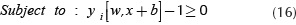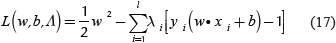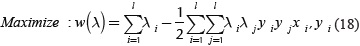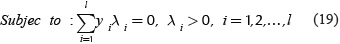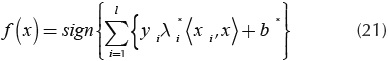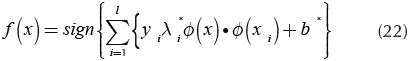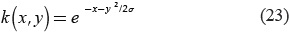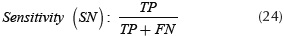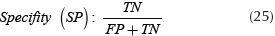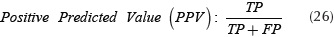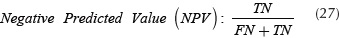Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.37 no.1 Bogotá Jan./Apr. 2017
https://doi.org/10.15446/ing.investig.v37n1.54703
DOI: http://dx.doi.org/10.15446/ing.investig.v37n1.54703
Weed recognition by SVM texture feature classification in outdoor vegetable crop images
Reconocimiento de maleza por características de textura usando SVM en imágenes exteriores de cultivos de hortalizas
Camilo Pulido1, Leonardo Solaque2, and Nelson Velasco3
1 Mechatronics Engineer, Universidad Militar Nueva Granada, Colombia -UMNG. Research Assistant, UMNG, Bogotá, Colombia. E-mail: camilopulidorojas@gmail.com
2 Electronics Engineer, Universidad de Antioquia, Colombia. Docteur de L'INSA Specialite Systemes Automatiques, L'institut National Des Sciences Appliquées, France. Professor Titular, UMNG, Bogotá, Colombia. E-mail: leonardo.solaque@unimilitar.edu.co.
3 Mechatronics Engineer, Universidad Militar Nueva Granada- UMNG, Colombia. Master of Science, Universidad Nacional, Colombia. Professor Assistant, UMNG, Bogotá, Colombia. E-mail: nelson.velasco@unimilitar.edu.co.
How cite: Pulido, C. Solaque, L., and Velasco, N. (2017). Weed recognition by SVM texture feature classification in outdoor vegetable crop images. Ingeniería e Investigación, 37(1), 68-74. DOI: 10.15446/ing.investig.v37n1.54703.
Received: December 15th 2015 Accepted: February 7th 2017
ABSTRACT
This paper presents a classification system for weeds and vegetables from outdoor crop images. The classifier is based on Support Vector Machine (SVM) with its extension to the nonlinear case, using the Radial Basis Function (RBF) and optimizing its scale parameter a to smooth the boundary decision. The feature space is the result of Principal Component Analysis (PCA) for 10 texture measurements calculated from Gray Level Co-occurrence Matrices (GLCM). The results indicate that classifier performance is above 90%, validated with specificity, sensitivity and precision calculations.
Keywords: Weed recognition, support vectors, co-occurrence matrix, PCA.
RESUMEN
El presente trabajo muestra un sistema de clasificación de maleza y hortalizas a partir de imágenes exteriores de cultivos. El clasificador está basado en la teoría de las máquinas de vectores de soporte (Support Vector Machine o SVM) con su extensión para el caso no lineal, haciendo uso de la función de base radial (RBF) y optimizando su parámetro de escala a para suavizar la región de decisión. El espacio de características es el resultado del análisis por componentes principales (PCA) de 10 medidas de textura calculadas a partir de matrices de co-ocurrencia en niveles de gris (GLCM). Los resultados indican un rendimiento del clasificador por encima del 90%, calculando los índices de especificidad, sensibilidad y precisión.
Palabras clave: Reconocimiento de maleza, vectores de soporte, matrices de co-ocurrencia, PCA.
Introduction
Weeds are plants that compete with the desired commercial crop, lowering productivity. They do this by blocking irrigation canals and by competing for water, nutrients, space, and light, consequently, the quality and crop yield decreases. A robotics application that can discriminate between weeds and crops from images is a cost-effective alternative to allow selective treatment to focus on optimizing resources and preserving environments, by identifying and removing only weed plants mixed with vegetables in crops. This approach can be solved using images processing to select undesired plants and by making an autonomous mechanical eradication on a mobile platform moving through crop, without affecting the other plants using chemical products.
Recent developments on the field of machine vision have led to a renewed interest in implementing weed recognition systems based on it. Basically, there are three main approaches for weed detection: based on colour, shape and texture analysis. Relating to colour and shape features, previous research suggests a criterion for segmenting plants based on a Vegetation Index that emphasizes the "green" component of the source image. Two such indices are the Excess Green Index (Woebbecke, et al., 1995), (Muangkasem, et al., 2010) and the Normalized Difference Vegetation Index using for weed classification considering color and shape (Pérez et al., 2000) and quantify map vegetative cover (Wiles, 2011). An advantage of indices is that they may perform well with different sunlight and background conditions, as a side effect. Colour features can be complemented with shape features that describe their geometry. If weeds can be identified by using shapes, then they can be identified by using area, perimeter, convexity and longest chord calculations (Shinde & Shukla, 2014).
Other studies have been carried out for weed classification with texture features using texture measures calculated on the basis of the Gray Level Co-Occurrence Matrix (GLCM) (Haralick, et al., 1973 and Burks, 1997), which preserves the spatial and high and texture descriptors have been used for training neural networks to identify plant species or weeds; numerous researchers have explained this approach, some of the most relevant articles are shown in Huang K. (2007) and Kavdir I. (2004) with classification accuaracy around 90%. Wu & Wen (2009) proposed a support vector machine classifier to identify weeds in corn fields during early crop stages, using the co-occurrence matrix in gray levels and statistical histogram properties to extract texture features with greater accuracy to 92%. Similarly, Ahmed, et al. (2012) evaluate fourteen colour, size and moment invariant features to get an optimal combination that provides the highest classification rate; their result achieves above 97% accuracy.
Based on studies described above, there exists a potential of using texture features to discriminate weed and vegetables applied to classifiers design and so to be carried to agriculture robotic applications. The main objective of the research presented in this paper is to develop a weed identification system using GLCM texture features extraction and their dimensionality reduction using Principal Component Analysis (PCA) to get suitable patterns in 2D feature space for training a support vector machine classifier from outdoor and unfiltered RGB images. The data processing system consists of a 3,30 GHz processor and 8GB RAM running MATLAB 2015b.
This paper has been divided into five parts. The first part is the Introduction; section 2 describes texture feature calculation and dimensionality reduction. In section 3, Support Vector Machine training is explained. Results and discussion are in section 4. The final part 5 is about conclusions and future work. Finally, acknowledgements are presented.
Texture Feature Processing using PCA
Texture features quantify, in various ways, grey levels differences. Building texture calculations over an entire image makes visible areas where these changes occur. Processing for texture features extraction contains a data base with outdoor vegetables crops images for SVM training, including labeled images according to weed and vegetables classes. Then, Grey Level Co-Occurrence Matrix method (GLCM) is purposed for each observation in the training set, where each matrix calculated serves as a basis to compute 10 statistical texture measures. Then, Principal Component Analysis (PCA) is used to represent original data in a new base where most variance is preserved on each axis; as a result, dimensionality reduction is performed to get a 2D feature space which procedure is described below.
GLCM and texture feature extraction
The GLCM method is a practical way to organize and tabulate the changes in brightness for different combinations of pixels, preserving the spatial information, getting first and second order texture measures, obtaining statistical calculations considering or not the relationship between neighboring pixels. The mathematical definition of cooccurrence matrix is shown in the Equation (1).
Where C, is a co-occurrence matrix defined over an I image with m x n size, parameterized with steps Δx and Δx. This matrix must be modified in such a way diagonal and normalized according to Haralick, et al., (1973) for texture calculations. The present paper works with ten texture measures computed from the co-occurrence matrix. These features were selected for cover three groups: contrast, order and descriptive statistics. Likewise, these quantify similarity or local variance in the image, deviation of the gray levels, co-occurrence frequency of pixels, uniformity and homogeneity of the image within the image evaluation. The mathematical expressions about texture features are shown in Equations (2) - (11).
Where Nx and Ny are the columns and rows respectively to rectangular image, quantized in Ng gray levels and p(i,j) are the input (i,j)ith of the normalized GLCM.
The database of images was built using 250 photos captured by a person moving along vegetable crops using an 8MP camera perpendicular to crop lines, avoiding illumination disturbances in a not-automated manner, controlling the lens aperture for redu-cing light input to preserve the real color of the plants. Although this process was manual, it is a first approach to testing the present weed classification based on texture descriptors, and even more thinking about further work with light controlled conditions using a camera obscura. The photos used in this paper include spinach and chard crops of "Horticulture Technology", an academic program of Universidad Militar Nueva Granada Campus in Cajicá, Colombia. The images were labeled manually based on the random growth of weed and the expertise of crops manager to identify using a binary classifier between weed and plants classes.
With the dataset acquired, an observation with 100 x 100 pixels was built, dividing the original image into a grid. Some of the images used for feature extraction are shown in Figure 1.
It is important to highlight that the size of the observation was considered in this way, due to weed size. If the area was smaller, it would be a kind of zoom in and the little leafs of the weed could fill the entire window.
Then, texture measurements described above are calculated for each GLCM (observation with size of 100 x 100 pixels). Following this, results were stored and tabulated in a matrix of 250 rows for the observations and 10 columns representing the variables or texture descriptors.
PCA and dimensionality reduction
The Principal Component Analysis (PCA) is a multivariate method or tool used to find patterns in data, establishing a relationship of observed variables to detect trends, groups, deviations and outliers. The objective of the analysis is to represent the data in terms of a Y matrix that contains the greatest variance information in the directions of their eigenvectors (see Equation (12)), from X matrix with n columns for samples and m rows assigned to variables (Reddy, et al., 2012).
The principal components a result from eigenvectors of normalized covariance matrix of X, which are orthogonal to each other and sorted in descending order respect to eigenvalues (proportion of total dataset variance). Eigenvalues, therefore, indicate the proportion of variance and importance (length) of each principal component axis. To clarify, PCA calculation should be with the normalized data, subtracting the mean and divided by standard deviation, in order to avoid a large variance values due to measuring range and units of the extracted texture features.
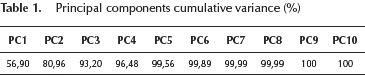
For the purpose of increasing the reliability of weed classification, a dimensionality reduction is carried out preserving the greatest variance in the data, thus, the eigenchannels derived from the texture descriptors and containing the majority of the input variance are those that best describe the features resulting from the linear combination of all calculated texture statistics for this particular image. The PCA calculation is performed on training set and the cumulative variances are shown in 1.
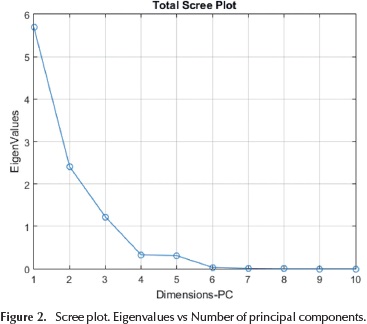
Moreover, another way of analyzing the principal component relevance for dimensionality reduction is through scree plot that represents eigenvalues versus number of components (See Figure 2).
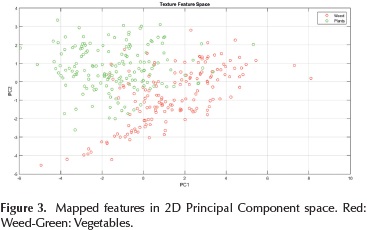
The descriptors must contain the most information possible about classes to discriminate them. In the same way, this corresponds to the direction with the greatest variance (eigenvalues) in the data. With this in mind, the first two components retain 80,96% of the data variance. For the purpose to validate a clear difference between weed and vegetable classes in 2D principal component space, the training set is transformed using eigenvectors obtained and graphed in Figure 3.
Support Vector Machine classification
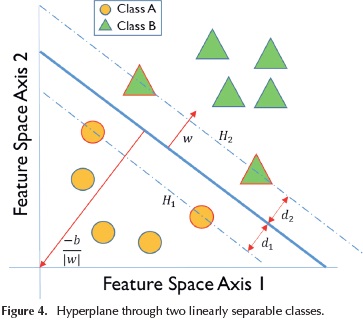
Support Vector Machine (SVM) is a discriminative classifier formally defined by a separating hyperplane. Support vectors are the closest examples to the separating hyperplane, and the aim of SVM is to orientate this hyperplane in such a way as to be as far as possible (margin) from the closest members of both classes. This separating hyperplane works as the decision surface and is described by wx+b=0, where w is normal to the hyperplane and b/||w|| is the perpendicular distance from the hyperplane to the origin. The Figure 4 shows a decision boundary example for discriminating two classes A (Circles) and B (Triangles) corresponding to vectors xi of the training set, with yi class labels of +1 and -1 respectively. The hyperplane's equidistance from H1 and H2 (d1+d2) means a quantity known as margin.
Then, the SVM approach is based on selecting the variables w and b to describe training data using Equations (13) and (14).
In order to orientate the hyperplane to be far from the Support Vectors, it is necessary to maximize the margin value 1/||w||. This implies to:
This is a convex quadratic optimization problem, which than can be expressed as a dual problem with Lagrange Multipliers.
Where Λ=(λ1,..., λl) is the vector of non-negative Lagrange multipliers corresponding to the constraints in Equation (16). Therefore, the dual problem is:
The optimal solution λ* is a discriminant function to classify new points in feature space. Equations (20) and (21) shows how is built this function. Where b* is a threshold value (Osuna, et al., 1997).
In most cases, the classification problems are nonlinear in feature space, then, SVM theory can be extended projecting input data to a higher dimensionality space, in which a separating hyperplane can be built. This approach is achieved using a kernel function given a suitable mapping x -> ø(x).
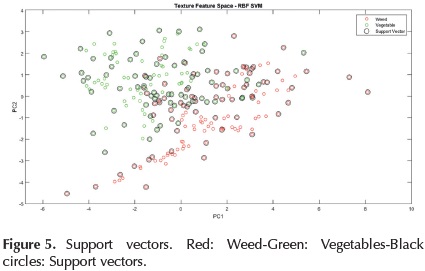
Up to now, this section has explained SVM theory; therefore, the methodology used to train will be set out. Figure 5 shows the highlighted support vectors (black circles) according to training set results from dimensionality reduction using PCA with texture features.
The radial basis function (RBF) is used as kernel to resolve weed classification problem due to the nonlinear representation of texture features in principal components space. The mathematical definition of RBF is exposed in Equation (23).
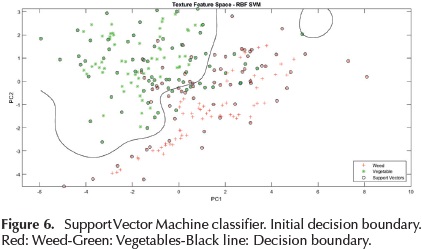
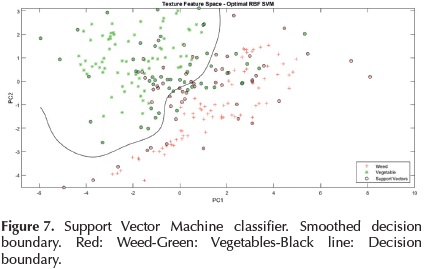
Figure 6 shows the contour of decision boundary corresponding to RBF kernel with σ=1 in training set.
To increase the reliability of weed discrimination, the support vector machine trained above is optimized. For this purpose, the training data is partitioned into 10 sets, then, 10-fold cross-validation loss is expressed as a function and it is used to find an optimal a value with the simplex search method of Lagarias et al., (1998). The resulting value of a is 0,9614 and the smoothed decision boundary is shown in Figure 7.
Results
The classification algorithm was tested with a set of images that contain weed and vegetable observations. As the training set, each observation has a size of 100 x 100 pixels and was taken perpendicular to crop lines, avoiding illumination. The experiments were carried out over two validation sets with a size of 70 and 320 samples, these experiments were labeled and stored respect their class in a column vector, with regard of classification performance indices calculations described in Equations (24), (25), (26) and (27).
Where True Positive (TP) is the number of plants detected as weed correctly. True Negative (TN) corresponds to the number of plants detected as crop correctly. False Positive (FP), the number of crop plants detected as weed and False Negative (FN), the number of weed plants detected as crop.
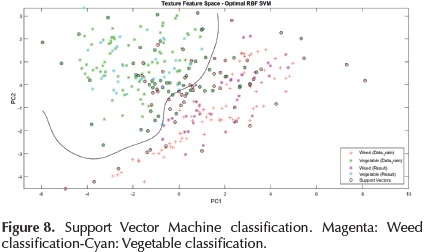
The first test was performed with a set of 70 images, 35 observations of weed, and the remaining, weed images. The results are shown in Figure 8, in which pattern or principal components space with the decision boundary is displayed, and the position of asterisks indicate weed (magenta) and vegetables (cyan) classification.
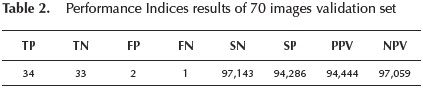
The classifier performance is tabulated in Table 2 with the indices calculation described above.
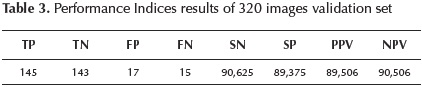
Another test was performed with a set of 320 images, half corresponding to weed and the remaining to vegetable samples. Table 3 exposed the results achieved as performance indices.
Conclusions
The present study was designed to extract relevant features as patterns from texture measures, and use it for classify weed and vegetables. The approach used outdoor images without preprocessing and was validated according to the results of principal components analysis and the clear difference between classes exposed in feature space (See Figure 3), thereby, other algorithms to try outdoor conditions images are not necessary, and the computational cost is also reduced. The statistical measures of the performance of classifier indicate: Sensitivity and specificity values above 90% represent a high percentage of correct classification of weed and vegetables according their true condition. Meanwhile, positive and negative predicted values describe a high accuracy, indicating the probability that a new sample can be really classified as weed or vegetable. These results suggest that the system classification developed has a high performance and can be applied for selective treatment of weeds or applications that requires continuous monitoring for minimizing resource consumption on agricultural productivity. Future work is focus on transfer coordinates from identification results of the crop scene to a mechanical structure as set-points to reach and pull out weed plants on a module that will be pulled by a tractor.
Acknowledgements
This work is supported by the project INV ING-1758 namely "Sistema de detección de malezas, suelo compacto, suelo seco, plagas y piedras en los campos de cultivo Fase 1", funded by the research vice D.R AVE rectory of the Universidad Militar Nueva Granada in Bogotá-Colombia.
References
Ahmed, F., Al-Mamun, H., Bari, A., Hossain, E., & Kwan, P. (2012). Classification of crops and weeds from digital images: A support vector machine approach. Crop Protection, 40, 98-104. [ Links ]
Burks, T. (1997). Color image texture analysis and neural network classification of weed species. [ Links ]
Cho, S., Lee, D., & Jeong, J. (2002). AE-Automation and Emerging Technologies: Weed-plant Discrimination by Machine Vision and Artificial Neural Network. Biosystems Engineering, 83(3), 275-280. [ Links ]
Haralick, R. M., & Shanmugam, K. (1973). Textural features for image classification. IEEE Transactions on systems, man, and cybernetics, 3(6), 610-621. [ Links ]
Huang, K.-Y. (2007). Application of artificial neural network for detecting Phalaenopsis seedling diseases using color and texture features. Computers and Electronics in Agriculture, 57, 3-11. [ Links ]
Kavdir, L (2004). Discrimination of sunflower, weed and soil by artificial neural networks. Computers and Electronics in Agriculture, 44(2), 153-160. [ Links ]
Lagarias, J. C., Reeds, J. A., Wright, M. H., & Wright, P. E. (1998). Convergence properties of the Nelder--Mead simplex method in low dimensions. SIAM Journal on optimization, 9(1), 112-147. [ Links ]
Muangkasem, A., Thainimit, S., Keinprasit, R., Isshiki, T., & Tangwongkit, R. (2010). Weed detection over between-row of sugarcane fields using machine vision with shadow robustness technique for variable rate herbicide applicator. Energy Research Journal, 1(2), 141-145. [ Links ]
Osuna, E., Freund, R., & Girosi, F. (1997). Support vector machines: Training and applications. [ Links ]
Pérez, A. J., López, F., Benlloch, J. V., & Christensen, S. (2000). Colour and shape analysis techniques for weed detection in cereal fields. Computers and electronics in agriculture, 25(3), 197-212. [ Links ]
Reddy, T. A., Devi, K. R., & Gangashetty, S. V. (2012, March). Nonlinear principal component analysis for seismic data compression. In Recent Advances in Information Technology (RAIT), 2012 1st International Conference on (pp. 927-932). IEEE. [ Links ]
Shinde, A. K., & Shukla, M. Y. (2014). Crop detection by machine vision for weed management. International Journal of Advances in Engineering & Technology, 7(3), 818. [ Links ]
Wiles, L. J. (2011). Software to quantify and map vegetative cover in fallow fields for weed management decisions. Computers and electronics in agriculture, 78(1), 106-115. [ Links ]
Woebbecke, D. M., Meyer, G. E., Von Bargen, K., & Mortensen, D. A. (1993, May). Plant species identification, size, and enumeration using machine vision techniques on near-binary images. In Applications in Optical Science and Engineering (pp. 208-219). International Society for Optics and Photonics. [ Links ]
Woebbecke, D. M., Meyer, G. E., Von Bargen, K., & Mortensen, D. A. (1995). Color indices for weed identification under various soil, residue, and lighting conditions. Transactions of the ASAE-American Society of Agricultural Engineers, 38(1), 259-270. [ Links ]
Wu, L., & Wen, Y. (2009). Weed/corn seedling recognition by support vector machine using texture features. African Journal of Agricultural Research, 4(9), 840-846. [ Links ]