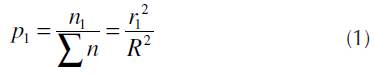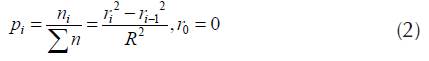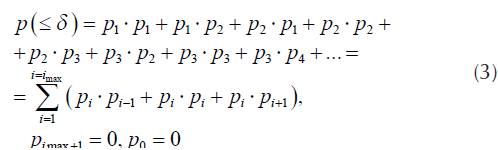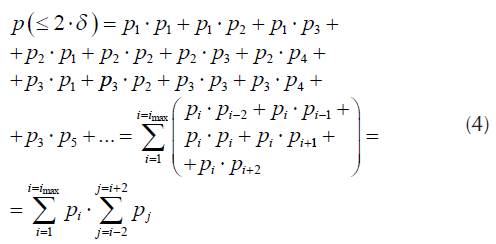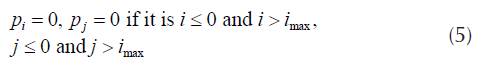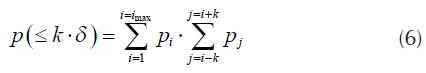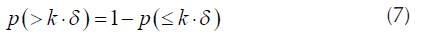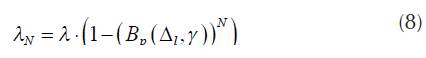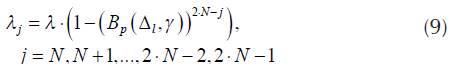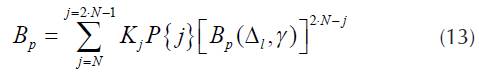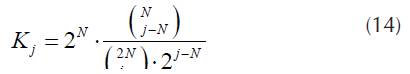Introduction
VAMOS (Voice service over Adaptive Multi-user channels on One Slot) technics significantly contribute to the increase of traffic capacity in classical GSM cell. This technics is implemented in GSM cell with frequency (FDMA) and time (TDMA) division multiplex, but each timeslot can be used for two connections (over two OSC, Orthogonal SubChannels). If full rate connections are applied, capacity may be doubled, and if half rate connections are applied, capacity may be quadrupled. In this way, the life cycle of GSM systems is prolonged, meaning GSM systems are "determined to stay", (Gerstacker et al., 2011). Besides increasing traffic capacity of GSM systems, there are also other developments related to these systems, which contribute to their "prolonged life". One possible direction of modernization is improvement in GPRS localization, as described in Paz et al. (2015).
The basic elements, which allow traffic capacity increase in GSM systems which implement VAMOS technics, are an implementation of QPSK (Quadrature Phase-Shift Keying) modulation and TSC (orthogonal Training Sequence Codes), (Säily et al., 2011; Huang, 2010). This modulation (i.e. it's variant AQPSK (Adaptive Quadrature Phase-Shift Keying) or α - QPSK) is implemented in downlink direction, when signal is transmitted in the same time to both users over the same timeslot. Implementation of α - QPSK modulation in the downlink direction (from a base station (BS) towards a mobile station (MS), i.e. mobile user) allows us to send signals of different power level to MSs, using the same channel, if the attenuation to each of them is different. Thus each MS receives signal of approximately equal power. The process of two connections placing in the same timeslot is called pairing. The main limitation in the process of pairing is that power ratio of two connections, using the same timeslot (SCPIR - SubChannel Power Imbalance Ratio) is less than 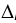 max
(dB).
max
(dB).
In this paper, we calculate the probability that the power level difference for two users dedicated to the same timeslot is too great, i.e. that user pairing is unsuccessful. Existing contributions, related to VAMOS technics, are presented in Section 2, where it is also emphasized what is the novelty of this paper. In Section 3, the cell model is presented and in Section 4, conditions for successful pairing are emphasized. In Section 5, the process of call arrival for pairing is presented, and the probability of unsuccessful pairing (unpairing) is calculated in Section 6. Numerical examples are given in Section 7. The traffic process simulation, which is used to estimate accuracy of the probability of unsuccessful pairing calculation, is presented in Section 8.
Previous contributions
Available literature, considering VAMOS systems, is not numerous. In Gerstacker et al. (2011) several types of VAMOS signal receivers are analyzed with the aim to reduce cochannel interference. Further analysis of interference cancellation may be found in Ruder et al. (2015). But, these two contributions are only enabling technology for VAMOS implementation to achieve the main goal to increase GSM system traffic capacity.
Traffic capacity duplication if full rate VAMOS channels are applied, and quadruplicating if half rate VAMOS channels are applied is just an approximation. A more precise analysis, which is based on Erlang traffic model consideration, is presented in Lebl et al. (2015) and illustrated in Enache (2015). This is the simplest analysis method, which shows that capacity increase is greater than it is expected, according to the approximation.
VAMOS function implementation is based on user pairing. The purpose of user pairing and classes of pairing possibilities are explained in Budura et al. (2014). There are two pairing strategies, as it is emphasized in Ruder et al., (2012): the first one is to pair all users, who can be paired, regardless of the number of busy channels (pure VAMOS) and the second one is to start user pairing when some threshold of the number of busy channels is reached. Contribution (Ruder, 2014) is complex study of user pairing, which includes results in Gerstacker et al. (2011); Ruder et al. (2015); Ruder et al. (2012)). It analyses influence of pairing on frame error rate (FER) and base station power per active user. In Ruder, (2014) also different receiver algorithms are analyzed (for example, Single Antenna Interference Cancelation (SAIC) and Mono Interference Cancelation (MIC)). According to available literature (Ruder, 2014), although it is the most comprehensive approach to user pairing consideration, it does not explicitly emphasize some factors, which have influence on the pairing possibilities. These factors are indirectly analyzed (or not analyzed): user distance from the base station and user distribution in the base station cell (when users are uniformly distributed in the cell, the maximum number of users is situated in the area annulus near the cell rim). In Ruder (2014) environment attenuation factor (γ) is only mentioned in an example, the influence of γ variation is not considered. The first contribution of our paper is that we analyze influence of these three important factors on pairing possibilities. The other novelty is that we consider call loss in VAMOS systems, which includes together traffic loss and loss caused by unsuccessful pairing and compare these results to the loss in pure Erlang systems. According to our knowledge, there is no such an analysis in literature.
Model, designation and assumptions
Let us consider a circular GSM cell, whose radius is R. The distribution of MSs in the cell is uniform, i.e. MS number per unit area of the cell is constant. Control of the emission power is applied in BS in the direction towards MSs. Distance between BS and MS is designated by r, 0 ≤ r ≤ R. Signal attenuation is designated by a. Attenuation coefficient which depends on the mutual distance between the MS and the BS is γ, a = k-r γ , k is the coefficient of proportionality and 2 ≤ γ≤ 5, (Ebersprächer et al., 1999). The number of timeslots used for traffic (TCH) is N and the number of MSs is M. The channels are mainly used for telephone traffic, which means that after the new request (new call) is generated in random moment; the connection must be established in a relatively short time interval, (ITU-T, 1999, ITU-T, 2000). Each user, i.e. MS, initiates a new call with the same intensity, so that the total offered traffic (A) is of constant intensity. The duration of the connection is random variable with the negative exponential distribution. The mean connection duration is t m = 1/μ, A = λ/μ = λt m It is assumed that N << M. The considered model is pure VAMOS, (Ruder, 2014), where all active MSs use VAMOS technics, i.e. maximal number of connections is 2-N.
Traffic model with full availability is analyzed in this paper, which means that call serving is with loss. The analyzed systems include application of VAMOS technics and they are not of Erlang type, because, due to pairing, the assumption that each request can seize each idle (sub) channel is not satisfied. In this paper the states of classical Erlang model are expressed as (j,A,2N), j = 0,1,.....2N-1, 2N. The probability that all channels in Erlang model are busy is designated as B e = P(2N,A,2N). The state probabilities in the considered VAMOS model are designated by P{j}, j = 0,1,.....2N-1, 2N, and the probability that all channels are busy by B=P{2N}. The difference in power, which is dedicated to the users with different attenuation, is (. The BS emission power towards MS is P, P m!n ≤ P ≤ P max . The power control in BS is realized in 15 steps of 2dB each one, (3rd Generation, 2001).
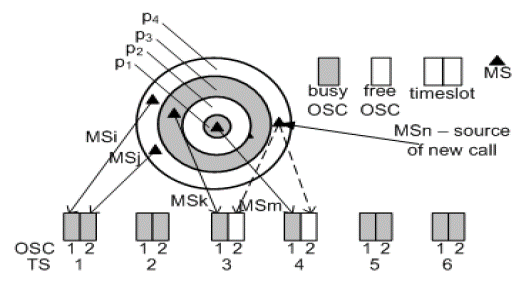
The cell model is symbolically presented in Figure 1. Continuous variation of attenuation in the cell is presented in Figure 1.1. Figure 1.2 shows effect of power control. The emission power changes (in steps of 2 dB), so that all users in the cell receive approximately the same power level. The lowest power level, P1, is intended for the users located in the circle of radius r 1 around BS. The signal of the next power level, P 2 , is sent to the users in the circular ring (annulus) whose inner radius is r 1 and external radius is r2, and so on. Figure 1.3 symbolically presents number of users in the circle around BS (n1) and in other annuli (n2, n3,...). The probability that the source or destination of the call are in a circle of radius r 1 or in an annulus is proportional to the area of that circle or that annulus. This probability is presented in Figure 1.4 and designated as p 1 , p 2 ,....
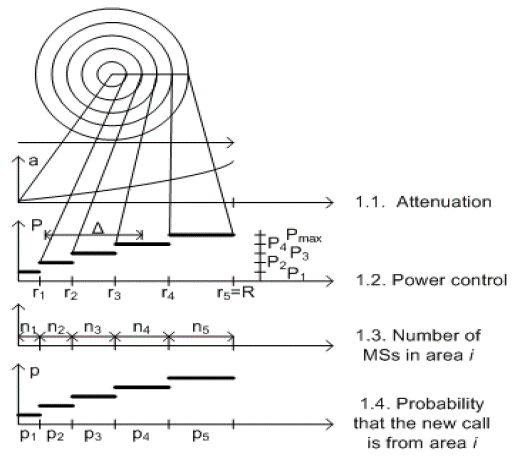
Source: Authors
Figure 1 Symbolical presentation of signal attenuation, emission power, number of MSs and the probability of new request generation in the parts (annuli) of the considered cell.
The difference in the required emission power for users with different attenuation is presented in Figure 1.2 and designated by symbol  .
.
Let us consider pairing of telephone connections, which have to be set up quickly after a request. Pairing two connections per timeslot is performed so that the difference in the required emission power in the direction from the BS to the MSs is less than the threshold limit value  l The values
l The values 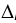 l
= 4dB,
l
= 4dB,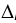 l
= 6dB, (Balint et al., 2014),
l
= 6dB, (Balint et al., 2014), 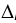 l
= 8dB and vl
= 10dB, (Das et al., 2014) are implemented in practice. The value of 10dB is considered the maximum applicable value of SCPIR, (Digital, 2016). If two calls vary according to the required power for more than
l
= 8dB and vl
= 10dB, (Das et al., 2014) are implemented in practice. The value of 10dB is considered the maximum applicable value of SCPIR, (Digital, 2016). If two calls vary according to the required power for more than 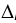 l, pairing attempt is considered unsuccessful. Unpaired call will be dedicated to another, completely idle timeslot, if such one exists.
l, pairing attempt is considered unsuccessful. Unpaired call will be dedicated to another, completely idle timeslot, if such one exists.
In the state where there is one or more idle subchannels, unsuccessful attempt of pairing in this paper can be conditionally called unpairing (unsuccessful pairing) probability, and this probability can be marked as B p . Determination of the probability of unsuccessful pairing is the basic aim of this paper.
Pairing technics
In this section pairing and conditions of unsuccessful pairing probability are explained on one simplified model.
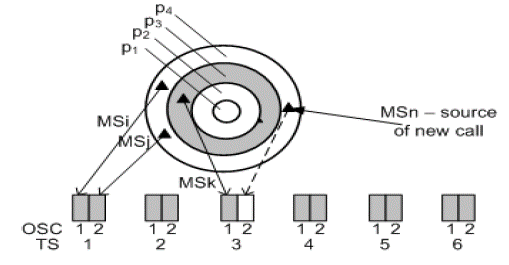
Pairing is done in such a way that two connections, for which the required power does not differ by more than Al, are combined in one timeslot, users MSi and MSj, Figure 2. Let us consider the group of 6 timeslots of which 4 are completely busy, i.e. occupied by paired connections. Two timeslots (TS3 and TS4) are half busy, i.e. only one OSC is busy in each of them. In a random moment appears a new call from the user MSn. The required power for the user MSn is greater than the power dedicated to OSC1 in TS3 and to OSC1 in TS4 for more than  l, i.e. | PMSn - PMSk| >
l, i.e. | PMSn - PMSk| >  l and | PMSn - PMSm | >
l and | PMSn - PMSm | > 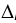 |. Pairing a new connection in timeslots TS3 and TS4 in this case is unsuccessful.
|. Pairing a new connection in timeslots TS3 and TS4 in this case is unsuccessful.
The probability of a successful pairing is proportional to the probability that a new call is coming from the annuli where the calls MSk and MSm belong, and it is P sp2 = (p 1 +p 3 )/ (p 1 +p 2 +p 3 +p 4 ), where p 1 , p 2 , p y p 4 (as in Figure 1) are the probabilities that the new call is initiated in annuli 1, 2, 3, 4. The probability of unsuccessful pairing is B p2 = 1-P sp2 .
Let us now consider the case when there is only one idle OSC, (OSC2, TS3), Figure 3. The probability of successful pairing is now P sp1 = p 3 /(p+p 2 +p 3 +p 4 ) and it is smaller than the probability of successful pairing when there are two idle OSCs, P sp2 . The probability of unpairing is Bp1 = 1-P sp1 .
It can be said that the probability of unsuccessful pairing for one call is as greater as there are less idle OSCs in that moment.
New calls
In this section method of pairing is explained on an example of a cell with maximum number of annuli.
Generation of new calls (for which the same power level is transmitted from the BS) in certain parts of the cell (circle and annuli) is random process, and the call rate is proportional to the surface of the considered part. The probability of call generation, or termination, in the circle of radius r1 around BS is
As users are uniformly distributed over the surface area which is covered by the considered cell, the probability that the connection source or destination is in the annuli i, i ≥ 1, is
Let δ(= 2dB) be the difference of signal power level, which is necessary to be sent to the users in adjacent areas (adjacent annuli). The probability, that difference of power level for two consecutive calls is not greater than δ is
The probability, that emission power for two consecutive calls is greater than δ is P(> δ) =1 - P(≤ δ).
The probability, that difference of power level for two consecutive calls is not greater than 2-δ is
Where
It is obvious that P(> 2-δ) = 1 - P(≤ 2-δ).
The probability, that difference of power level for two consecutive calls is not greater than k-δ is
also with the validity of the condition (5). The probability, that emission power for two consecutive calls is greater than k-δ is
These considerations are also valid when, instead of two consecutive calls, we analyze two calls that need to be paired in one timeslot.
The question is how the coefficient of attenuation affects the probability of successful or unsuccessful pairing. It is clear that an increase of attenuation coefficient produces the decrease of the annulus area that is covered with an attenuation of 2dB. That's why the number of users, who are located in parts of the cells where necessary power varies less than Al relative to the considered user, is smaller if γ is larger. It can be concluded that the probability of successful pairing is as smaller as attenuation coefficient is greater.
The probability P(> k-δ) that two calls can't be paired in one time slot is designated as B p (A,1).
Calculation of the probability of unpairing
In this section calculation of unsuccessful pairing probability is presented when there is various number of busy OSCs.
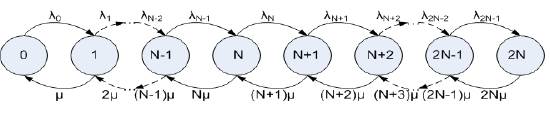
Let us consider the group of N timeslots, i.e. 2-N OSCs. The state of the system is designated by {j}, j = 0,1,2,...2N-1,2N, where j is the number of busy OSCs, and P{j} is the probability that system is in the state {j}. Unsuccessful pairing is overcome by taking an OSC in an idle timeslot, if idle timeslot exists. Unsuccessful pairing is, theoretically, possible in all states where it is j ≥ N,Figure 4a). Figure 4b) presents the group where it is j ≥ N, but with such position of busy OSCs that, when new call is generated, it will be paired in OSC2 of TS3, or it will be realized in TS4. In the situation presented in Figure 4a) it is possible (although with low probability) that a new call cannot be paired with any of existing calls.
Source: Authors
Figure 4 An example where pairing can be impossible (Figure 4a)) and where the connection is always realized (Figure 4b)).
The state probabilities can be calculated if we consider the state diagram, (Iversen 2015), section 4.2.2. Figure 5 presents possible states and transitions between states. It is important to emphasize that call arrival rates in states j = 0,1,2,....N-2,N-1 are equal, i.e. λ0 = λ 1 = ... = λ Ν2 = λ Ν1 = λ. In conditions j > N pairing can be unsuccessful, which means that offered call intensity is not realized completely in established connections.
The part of traffic arrival rate represents unsuccessful pairing. In the state N traffic arrival rate intensity is reduced by the part that is not realized due to unsuccessful pairing:
In Equation (8), the part of traffic, which is not realized, is expressed as the product of call arrival rate (λ) and the probability of unsuccessful pairing 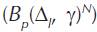 . Generally, for the state N ≤ j <2-N
. Generally, for the state N ≤ j <2-N
i.e. traffic arrival rate is equal to the product of call intensity and the probability that there is no unsuccessful pairing.
If the system is in statistical equilibrium, then the cut equations are valid, (Iversen, 2015)
On the base of these equations, the state probabilities can be determined as:
provided that
Now the total unpairing probability in all states where unpairing is possible can be determined as
where K is probability that there are no free timeslots in state {j} is
It should be noted that there is also a loss due to the occupancy of all OSCs and it is
The unpairing probability B
p
depends on traffic (λ/μ), attenuation coefficient (γ) and allowed difference in the power of paired connections (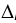 l).
l).
The unpairing probability is greater if the offered traffic is greater and it is the general rule at all serving systems.
As it is emphasized in Section 4, the unpairing probability is greater if the attenuation coefficient is greater.
The unpairing probability is greater if the allowed difference in the power of paired connections is smaller, as there are fewer users in areas -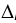 l, +
l, + 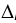 r
r
Numerical examples
Characteristics of GSM cell with implemented VAMOS technics are illustrated by several examples. It is analyzed the dependence of the unsuccessful pairing probability on the traffic load, allowed signal level difference of two paired connections and attenuation coefficient.
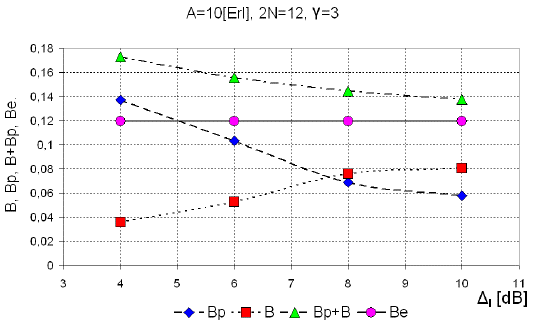
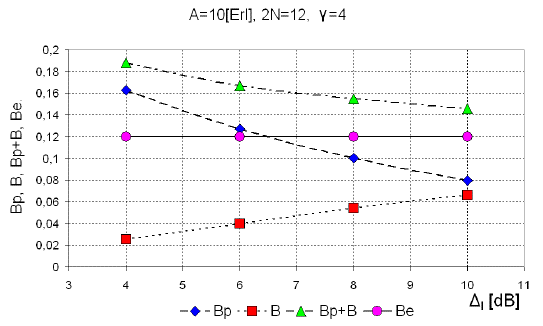
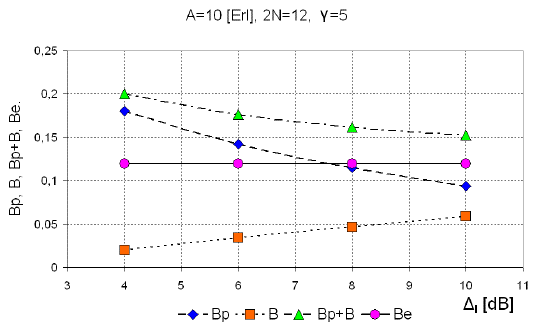
Figures 6, 7 and 8 present dependence of the probability of unsuccessful pairing, Bp, Equation (13), blocking probability, B, equation (15) and their sum B p + B, on the allowed signal level difference (Δ l ) between two paired connections for the group of N = 6 timeslots with the offered traffic load 10 Erlangs (10Erl), for the cases γ = 3, γ = 4 and γ = 5. It should be noted that in classical Erlang group with 12 channels technics, and the blocking probability in Erlang group, as and offered traffic 10Erl the loss is B=P(12,10,12)=0.1197.
Source: Authors. Results were obtained by simulation
Figure 6 Probability of unsuccessful pairing (Bp), blocking probability (B), the sum B p + B and Erlang loss (Be) as the function of allowed difference (Δl) in level of signals, which are paired for γ = 3.
Source: Authors. Results were obtained by simulation
Figure 7 Probability of unsuccessful pairing (Bp), blocking probability (B), the sum B p + B and Erlang loss (Be) as the function of allowed difference (Δl) in level of signals, which are paired for γ = 4.
Source: Authors. Results were obtained by simulation
Figure 8 Probability of unsuccessful pairing (Bp), blocking probability (B), the sum B p + B and Erlang loss (Be) as the function of allowed difference (Δl) in level of signals, which are paired for γ = 5.
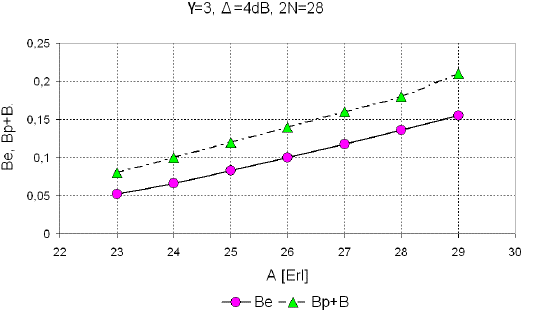
Figure 9 presents dependence of the sum B p + B in the group of N = 14 timeslots (2N = 28 OSCs), which uses VAMOS technics, and the blocking probability in Erlang group, as the function of traffic, γ = 3, Δ = 4dB.
Source: Authors. Results were obtained by simulation
Figure 9 A comparison of the sum of the unpairing probability an blocking (Bp + B) with the blocking probability in Erlang group (Be).
Figure 10 presents dependence of unpairing probability on the attenuation coefficient. This dependence is in accordance with the statement set out at the end of Section 4. Considered group of channels is as in the examples of Figures 6-8, and allowed difference in power between two paired connections is Δ l = 6dB. It may be noted the fact that the probability of unsuccessful pairing B p ,Equation (13), increases when attenuation coefficient increases, but the loss probability, due to occupancy of all channels, drops.
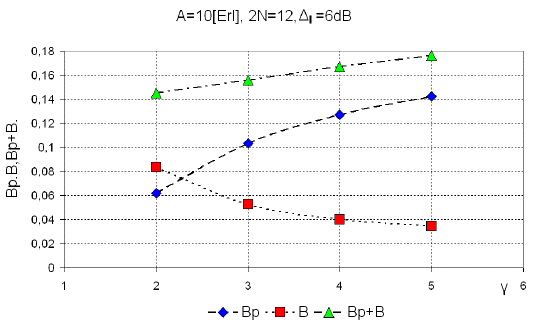
Source: Authors. Results were obtained by simulation
Figure 10 Unpairing probability (Bp), blocking probability (B), and the sum Bp+B as the function of attenuation coefficient γ.
Figure 11 presents distributions of system states P{j} j = 0,1,...2N for the group of N = 6 timeslots, which uses VAMOS technics. The offered traffic to this group is 10Erl. The distributions are obtained by calculation and simulation (mean value of three simulation trials). As can be seen from the graph in Figure 11, the results of calculation and simulation satisfactorily agree one to the other.
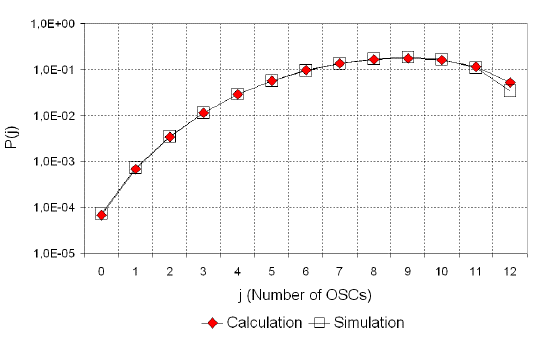
Source: Authors
Figure 11 Comparison of the probabilities of VAMOS system states obtained by calculation and simulation.
Each simulation trial in this contribution is performed till at least 300000 offered calls, i.e. more than 20000 calls per channel.
Simulation
Verification of the results is realized by simulating the process of channel seizure and release in one GSM cell. The simulation process is based on Rou׳ette or Monte Car׳o method, (Jeruchim et al 2002, Akimaru et al 1992). The starting point in simulation is software generation of (quasi)random numbers, which is one of methods to obtain random sequence of numbers. The detailed survey of different methods for random number generation is presented in López-Leyva et al (2016)).
The main purpose of simulation in this paper is to compare the results of simulation and the results of calculating the probability of unsuccessful pairing. Besides its primary objective, the purpose of simulation is also to verify how much the state distribution probability for the group that contains 2N OSCs deviates from the state distribution probability for the classical Erlang full availability group.
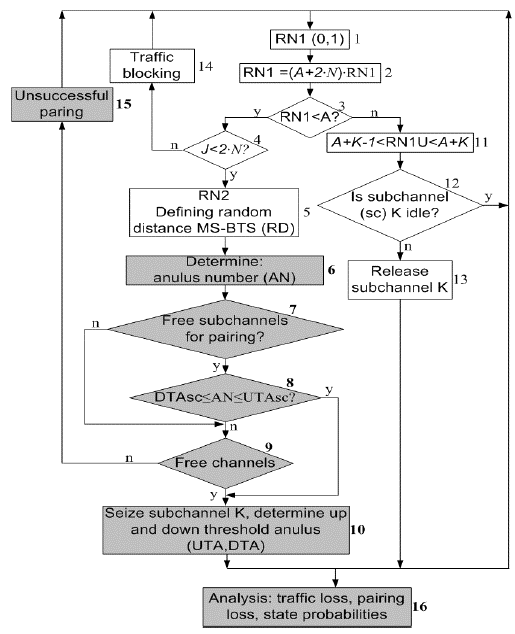
The simulation program is similar to the programs implemented in Mileusnić, Šuh et al (2014) Mileusnić, Jovanović et al (2014) and Mitić et al (2016) and it is briefly presented in the Figure 12. The parts of simulation program, which differ from the simulation steps presented in Mileusnić, Šuh et al (2014).Mileusnić, Jovanović et al (2014). Mitić et al (2016) are specially highlighted (by grey shaded blocks). The parts of simulation program already presented in Mileusnić, Šuh et al (2014), Mileusnić, Jovanović et al (2014), Mitić et al (2016) include generation of traffic process and determination of the distance between BS and MS on the basis of generated random numbers. Instead of the number of channels in the system, in the places where it is necessary is figuring the number of subchannels (2N in blocks 2 and 4).
After determination of mutual distance between BS and MS, the area (number of the annulus or the circle next to the BS in which mobile user, participant in a connection, is located) is determined in block 6. After that, it is checked whether the call can be realized. It is first tested whether the new connection can be paired with some of already existing connections. Pairing can be realized if at least one idle OSC exists in the pair where one OSC is already busy (block 7) and if the annulus (AN), where the new offered call is located, is between the upper (UTAsc) and lower (DTAsc) previously defined threshold for some of currently unpaired OSCs (block 8). If pairing cannot be realized with any of previously active OSCs, when the second OSC in the pair is idle, it is tested in block 9 whether some completely idle channel exists (i.e. channel with two idle OSCs). If there are no such channels, the pairing impossibility is declared (block 15). Therefore, in the case of VAMOS system simulation, besides blocking caused by the lack of idle OSCs - traffic blocking (block 14), unsuccessful pairing, caused by pairing impossibility, must be also predicted (block 15).
The new offered connection can be established if pairing can be realized or if some completely idle channel exists. In that case, one OSC is seized in the block 10 and upper and lower threshold (annulus) is determined for possible future pairing.
At the end of simulation, the elements, which are important for the analysis, are determined in block 16: the probability of traffic loss, the probability of unsuccessful pairing and the probabilities of system states (i.e. probabilities of the number of busy OSCs).
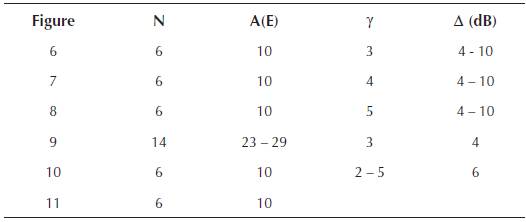
Simulation parameters for various simulation trials in this paper are summarized and it is shown in Table 1. In this table these parameters are emphasized separately, for each Figure with presented results (6 - 11). The input parameters, which are varied, are number of timeslots (N), offered traffic A (E), attenuation coefficient (γ) and allowed power difference for two mobile users to be successfully paired (Δ (dB)).
Conclusions
Besides classical loss due to lack of idle channels (blocking), in the GSM cell, which uses VAMOS technics, there exists the probability of unsuccessful pairing in OSCs of the same timeslots. Pairing is unsuccessful if the difference in required emission power for two considered connections is greater than the allowed threshold. In the group of 2N OSCs unsuccessful pairing may happen when the number of busy OSCs is greater or equal to N. The probability of unsuccessful pairing is greater if the offered traffic is greater, if the difference in allowed emission power for paired connections in the same timeslot is smaller and if the attenuation coefficient is greater. Comparison of blocking probability in Erlang model Be=P(2N,A,2N) and the sum of blocking probability and the probability of unsuccessful pairing (S=Bp+B) in normal traffic conditions shows that it is S>Be, but not more than two times. The results of calculation in numerical examples are compared to the results of simulation, for which a special program is developed by upgrading some well-known programs.