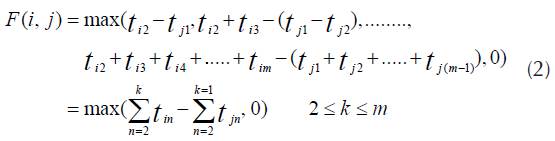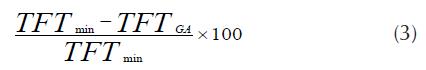Introduction
Scheduling is an important aspect of any manufacturing concern. The importance of efficient scheduling function cannot be denied as it ensures timely dispatch of products to the market before the competitors, thus yielding higher profits. The primary objective in any scheduling problem is to efficiently allocate jobs to the available machines and to determine the start and ending time of each operation, such that certain objective function is minimised or maximised. The schedule developed should also satisfy various production constraints. In order to achieve high-efficiency production, efficient scheduling algorithms/schemes are therefore considered to be a key factor.
Flow shop scheduling is one of the widely studied models of the manufacturing environment. In a general flow shop scheduling problem, there are n-jobs that are required to be scheduled on m-machines to typically minimise total completion time or makespan. All jobs follow the same processing order. The flow shop scheduling problem has received considerable attention since its introduction in 1954 (Johnson, 1954). Over the years, numerous efficient techniques and meta-heuristics have been proposed by various researchers. Gupta et al. (2006) has given a detailed survey of flow shop scheduling research. Tyagi et al. (2013) also present a survey of the evolution of flow shop scheduling problems and possible approaches for their solution.
No-wait flow shop (NWFS) is an extension of general flow shop, where all the operations of a particular job are required to be processed in a continuous manner, i.e. there are no intermediate buffers between the machines and all operations are to be processed without interruptions. Pharmaceutical processing, concrete ware production, oil refineries, etc., are some examples of no-wait flow shop scheduling. A comprehensive analysis of research and applications of NWFS has been made by Hall et al. (1996). The problem is categorised to be NP-hard even for a simple 3-machine case (Hans, 1984).
In this paper, a NWFS scheduling problem is presented, where the objective is to minimise total flowtime of all jobs. A spreadsheet-based genetic algorithm (GA) is proposed for the problem. Empirical analysis has been made for flow shop benchmark problems proposed by Carlier (1978), Reeves (1995), Heller (1960) and Taillard (1993). The performance of the proposed GA is compared with different meta-heuristics that have been reported earlier in the published literature. The rest of this paper is organised as follows: Section 2 gives an overview of past research for minimisation of total flowtime in NWFS scheduling environment. Section 3 gives problem definition and assumptions. Brief overview of GA and its components is given in section 4. Section 5 presents implementation details of Reddi et al. (1972) equation for no-wait flow shop model with a numerical example. Section 6 presents empirical analysis for various benchmark problems taken from already published literature. Finally, section 7 concludes the paper.
Past Research
The first reported instance to address no-wait scenario in flow shop scheduling was presented by Reddi et al. (1972). The authors converted the corresponding problem into a travelling salesman problem and solved it in polynomial time by using an algorithm proposed by Gilmore et al. (1964). Due to the large number of research papers available on no-wait flow shop scheduling, we will restrict the literature review to the papers addressing only the objective function of flowtime that were published from year 2011 onwards.
Gao et al. (2011a) minimise total flowtime in NWFS problem using a discrete harmony search algorithm (DHS). In the first step, job permutation is represented by a harmony. Harmony memory is then initialised by using a new heuristic based on the NEH heuristic method (Nawaz et al. (1983). In the second step, novel pitch adjustment rule is employed in the improvisation to produce a new harmony. The local exploitation ability of the algorithm is enhanced by embedding a local search procedure. Laha et al. (2011) also minimise total flowtime by a constructive heuristic. The priority of a job in a sequence is determined by the sum of its processing times on the bottleneck machine(s). Computational experiments show that the proposed heuristic performs significantly well compared to Bertolissi heuristic Bertolissi (2000). Shafaei et al. (2011) minimise mean flowtime in a two-stage flexible no-wait flow shop problem. The authors develop six meta-heuristic algorithms based on imperialist competitive algorithm (ICA), ant colony optimisation (ACO) and particle swarm optimisation (PSO) to solve the problem. Then, they use 36 different problems (18 small and 18 large-scale problems) to test the performance of the algorithms. The results of the numerical experiments show that the proposed algorithms significantly outperform other algorithms in terms of solution quality and CPU time.
Gao et al. (2012) also consider minimisation of total flowtime in a NWFS scheduling problem using a hybrid harmony search (HHS) algorithm. NEH heuristic (Nawaz et al. (1983) is firstly used to form an initial harmony memory. Secondly, this memory is divided into several small groups, where each group independently executes its evolution process. However, all groups share information reciprocally by dynamic re-grouping mechanism. Thirdly, a variable neighbourhood search algorithm (VNS) is embedded in the HHS algorithm to stress the balance between global and local exploration. A speed-up method is applied to reduce the running time requirement. Computational simulations are carried out on well-known benchmark problems. The results show that the proposed HHS outperforms other methods published in the literature.
Guang et al. (2012) consider multi-objective NWFS problem using an evolved discrete harmony search algorithm to minimise total makespan, maximum tardiness and total flowtime. A job-permutation-based encoding scheme is applied to enable the continuous harmony search algorithm to be used for all sequencing problems. An archive set of non-dominated solutions is dynamically updated during the search process. The authors demonstrate that the proposed algorithm produces superior quality solutions in terms of searching diversity level, efficiency and quality. Tasgetiren et al. (2013) also consider a multi-objective NWFS problem to minimise the makespan and total flowtime. A variable iterated greedy algorithm with differential evolution is proposed to solve the problem. A differential evolution algorithm is used to optimise the parameters of the iterated greedy algorithm. Gao et al. (2013) present four composite and two constructive heuristics to minimise the flowtime.
The heuristics are based on constructive heuristic proposed by Laha et al. (2008), Bertolliso heuristic (Bertolissi, 2000) and standard deviation heuristic (Gao et al., 2011a). The performance of the proposed heuristics is tested on benchmark flow shop problems already published in the literature. Experimental results show that the proposed heuristics perform better than the existing ones.
Sapkal et al. (2013) propose a constructive heuristic to minimise flowtime. In the initial sequence, the sum of processing times of individual jobs on the bottleneck machines are used to prioritise the jobs. Final job sequence is obtained by a new job insertion technique based on NEH heuristic (Nawaz et al., 1983)1983. The authors demonstrate that the proposed heuristic outperforms Rajendran et al. (1990) and Bertolissi (2000) heuristics without effecting the average computational time. Akhshabi et al. (2014) propose a hybrid algorithm based on particle swarm optimisation (PSO) and a local search method to minimise total flowtime. Laha et al. (2014a) minimise total flowtime by a penalty-shift-insertion algorithm. A penalty-based heuristic derived from Vogel's approximation method for classic transportation problem is used to generate the initial sequence. In the second phase, a forward shift heuristic is used to improve the solution. The solution is further improved by a job-pair and a single-job insertion heuristic. Laha et al. (2014b) also propose a constructive heuristic to minimise flowtime in a NWFS scheduling problem. Similarly, Chaudhry et al. (2014) also present a GA approach to minimise total flowtime in no-wait flow shop scheduling problem. The performance of the GA is compared with well-known benchmark problems.
Zhu et al. (2015) also propose an iterative search method to minimise flowtime. Huang et al. (2015) propose a new heuristic algorithm named "Ant colony optimization (ACO) with flexible update". The proposed heuristic overcomes the limitations of traditional ACO algorithm. Nagano et al. (2015) consider minimisation of flowtime in a NWFS with sequence dependent setup times. A constructive heuristic is proposed to minimise flowtime by breaking the problem into quarters. The performance of the proposed algorithm is compared with previously reported heuristic algorithms. Qi et al. (2016) also consider minimisation of flowtime by a fast-local neighbourhood search algorithm. The algorithm initially constructs an unscheduled job sequence according to the total processing time and standard deviation of jobs on the machines. In the first step, the job sequence is optimised using a basic neighbourhood search algorithm. Then, an innovative local neighbourhood search scheme is designed to search for the partial neighbourhood in each iterative processing and calculate its solution with an objective increment method. The experimental results show that the proposed approach performs better than previous approaches in terms of quality and robustness of the solution.
Ying et al. (2016) propose a self-adaptive ruin-and-recreate algorithm to minimise flowtime in a no-wait flow shop scenario. Bewoor et al. (2017a) present a hybrid PSO algorithm to solve this class of problem. The proposed algorithm initialises population efficiently with the NEH heuristic technique (Nawaz et al., 1983)1983 and uses an evolutionary search guided by PSO, as well as simulated annealing based on a local neighbourhood search to avoid getting stuck in local optima and to provide the appropriate balance of global exploration and local exploitation. Bewoor et al. (2017b) present a PSO algorithm to minimise flowtime in a no-wait flow shop problem. The authors show that the proposed PSO algorithm outperforms GA and Tabu Search (TS) algorithms. Bewoor et al. (2018) also present a hybrid PSO algorithm for minimisation of flowtime in a foundry. Extensive computational experiments are carried out based on various casting (job) characteristics viz. casting type, mould size and type of alloy, where size of job (n) is considered as 10, 12, 20, 50 and 100. Miyata et al. (2018) study the impact of preventive maintenance policies in the performance of constructive heuristics for the no-wait flow shop problem with total flowtime minimisation. Díaz Ramírez et al. (2018) apply a mixed integer programming for production-scheduling in a chemical industry that identifies lot size and product sequence to maximise profit.
The proposed GA presented here is an extension of earlier work (Chaudhry et al., 2014; Chaudhry et al., 2012). In the current research, we present a spreadsheet-based GA for a NWFS scheduling environment, where the objective is to minimise total flowtime. As compared to previous studies, the proposed approach is general purpose and domain independent whereby it can be used for the optimisation of any objective function without changing the spreadsheet model or the GA routine. Similarly, the spreadsheet model can be extended to cater for more machines and jobs without any change to the basic GA routine. Spreadsheets have been used extensively for scheduling, as highlighted by Astaiza A (2005) for examination scheduling.
Problem Description and Assumptions
The general no-wait flow shop scheduling can be described as follows: there are n jobs from a set of jobs {j = 1, 2, 3, 4..., n} that are required to be processed through m machines {k = 1, 2, 3, 4..., m}. Each job j has a sequence of m operations (oj1, oj2..., ojk) that are required to be processed through m machines in a continuous manner, such that the completion time of ojk is equal to the earliest start time of oj k+1 for k = 1, 2, 3..., m-1. In other words, there has to be no waiting time between successive operations of each of the n jobs. The problem is then to find the sequence of jobs that would minimise the total flowtime of all the jobs.
The flowtime criterion for a schedule provides the measure of the time that a job spends in the system. The total flowtime for a sequence of jobs is the sum of the completion times of all the jobs. Minimisation of total flowtime criterion leads to rapid turn-around of jobs, stable utilisation of resources, and minimisation of work-in-process inventory costs (Framinan et al., 2003) 2003. The total flowtime is thus given by:
where is the completion time of job j n on machine k m , if it is scheduled in r position.
Other assumptions in this study are as follows:
All jobs are available at t = 0.
Processing times of operations are known in advance and deterministic.
An operation once started cannot be disrupted, i.e. no pre-emption of operations and jobs.
A machine, at any time, can process at most one job only.
At any given time, each job can be processed on only one machine.
There are no setup times for preparing a machine to process an operation.
Time for the movement of jobs between machines is negligible.
Genetic Algorithms
Genetic Algorithms (GA) belong to population-based meta-heuristics that are based on Darwin's theory of natural evolution. GAs were first proposed by Holland (1975) and his colleagues at the University of Michigan. These are general algorithms that work well in variety of situations. They are quickly able to provide a reasonable solution to the problem as they can traverse through large search spaces fast. GAs are most effective in a search space for which little is known. The first reported application of GAs for scheduling was presented by Davis (1985). Delgado et al. (2005) have also applied genetic algorithms for scheduling manufacturing cell tasks. Similarly, Frutos et al. (2012) apply genetic algorithms for multi-objective scheduling procedures in non-standardised production processes.
GAs start with a population of solutions (prospective solutions called chromosomes). Solutions from one population are taken into the next population with a view of getting better solutions in successive generations. In the first step, based on the fitness, two parent solutions are selected to form a child solution by employing the crossover operator. Afterwards, crossover mutation is applied to make random changes in the solution and form newer solutions. The algorithm then compares the fitness of the child solutions with the rest of the members of the population thus using the principle of survival of the fittest to discard the worst performing member of the population.
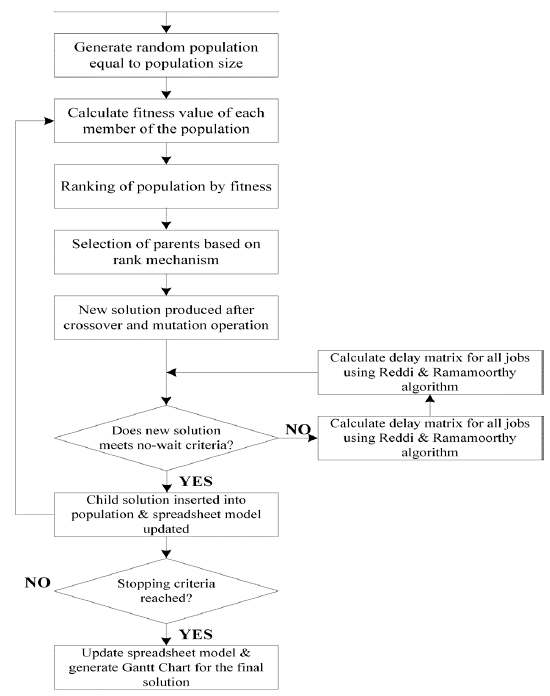
In this research, we have used permutation representation for the chromosome. For parent selection, rank-based selection method is used, while steady-state reproduction is used to produce offspring for the next generation (Whitley et al., 1988). For crossover operation, an order crossover (Davis, 1985) is used as it works best with the permutation representation by preserving the relative order of the genes and avoids duplicate genes in the chromosome. In the mutation operation, individual genes are swapped to form new chromosomes. The number of swaps increases or decreases corresponding to increase or decrease in the mutation rate. The details about various GA components, i.e., selection, reproduction, crossover and mutation, are given in Chaudhry et al. (2017). The flowchart of the GA as implemented in this research is shown in Figure 1.
Implementation Details
As stated earlier, the no-wait scheduling model in this research is based on the start delay matrix proposed by Reddi et al. (1972). This section describes the implementation details of this matrix.
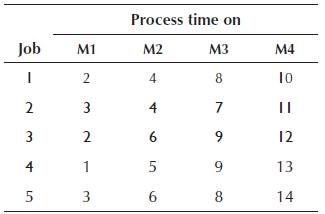
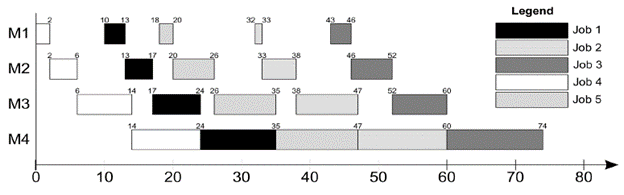
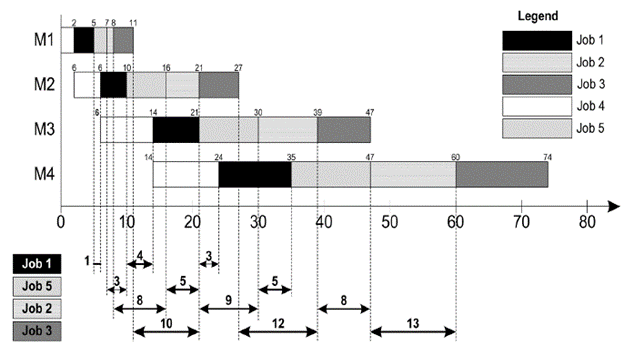
Consider a 5-job, 4-machine flow shop problem, as given in Table 1, where the objective is to minimise total flowtime. The optimal job sequence to minimise flowtime in the given problem is 4-1-5-2-3. The Gantt chart for the problem with waiting times between successive operations of the jobs is given in Figure 2. It can be seen from Figure 2 that Job 1 waits for 1, 4 and 3 time units between operation 1-2, 2-3 and 3-4, respectively. Waiting times between operation 1-2, 2-3 and 3-4 of Job 5 are 3, 5 and 5 time units, respectively. For Job 2, the waiting times are 8, 9 and 8 time units between operations 1-2, 2-3 and 3-4, respectively, whereas Job 3 waits for 10, 12 and 13 time units between operation 1-2, 2-3 and 3-4, respectively. As per no-wait constraint, all operations are required to be processed in continuation, i.e. there should not be any waiting time between successive operations of a particular job.
In this research work, we use a two-step procedure for the NWFS scheduling problem. The first stage calculates the delay factor for each job sequence. The start of the job is then delayed by as many time units as have been calculated in stage 1. Reddi et al. (1972) equation is used to calculate the delay factor for job i after job j.
If F (i, j) gives the minimum delay between the completion of job J. and the start of job J,, then the delay F (i, j) would be calculated by equation 2 (Reddi et al., 1972)1972, as follows:
From equation (2), we can observe that if job J. proceeds with no-wait in process, then the time to complete job J. is independent of the jobs that will precede and follow it. The minimum time for starting job J j after completion of J on the first machine, i.e. F(i, j), is the function of the parameters of job J i and J j only. Hence, the minimum timing of any sequence (j׳1, j 2 , j 3 , jn) must incorporate times F(i, j) between successive pairs of jobs J i , J j (Reddi et al., 1972)1972.
The corresponding schedule for the Gantt chart in Figure 2 would be as shown in Figure 3.
Source: Authors
Figure 2 Gantt chart for job sequence 4-1-5-2-3 with waiting times between the jobs.
Empirical Analysis
Empirical analysis was carried out to compare the performance of the proposed GA with earlier studies. The experiments were carried out on four different sets of benchmark problems taken from already published literature. The experiments were conducted on a Core i3 1,8 GHz computer with 4 GB RAM. Being a stochastic optimisation technique, the performance of a GA is dependent on different parameters, namely: crossover & mutation rates and the population size. Repeated tests were therefore conducted to determine the best set of values for aforesaid parameters. The best values were found to be 0,65 and 0,06, and 65 for crossover & mutation rates and the population size, respectively. Each problem was then run for 100 000 iterations that corresponded to 3 mins on the aforementioned computer. The results presented in the subsequent sub-section are based on 30 simulation runs, i.e. each problem instance is run for 30 times with random starting solution and subsequently noting the best value found for each instance. The % Diff is the relative difference of the best value found by all other algorithms (TFT min ) against the proposed GA algorithm (TFT GA ) and is calculated by equation 3:
Positive values indicate that the proposed GA found better results as compared to all other previous algorithms, while negative values indicate worse results.
Problem Set 1
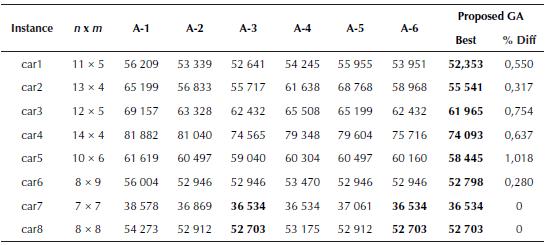
Problem set 1 consists of eight problem instances adapted from Carlier (1978). The results produced by GA have been compared with the following algorithms:
A-1: Grouping harmony search algorithm (Gao et al., 2011b)
A-2: Discrete differential evolution algorithm (Gao et al., 2011b)
A-3: Improved harmony search algorithm (Gao et al., 2011b)
A-4: Particle swarm optimisation algorithm (Dong et al., 2010)
A-5: Differential evolution algorithm (Dong et al., 2010)
A-6: Hybrid differential evolution algorithm (Dong et al., 2010)
The proposed GA approach found better results for six problems, while same results for two problems. Comparative results for total flowtime values of algorithms A1 - A6 and the proposed GA algorithm are presented in Table 2.
Table 2 Total flowtime comparison for algorithms A-1 to A-6 for Carlier (1978) data set
Source: Authors
Problem Set 2
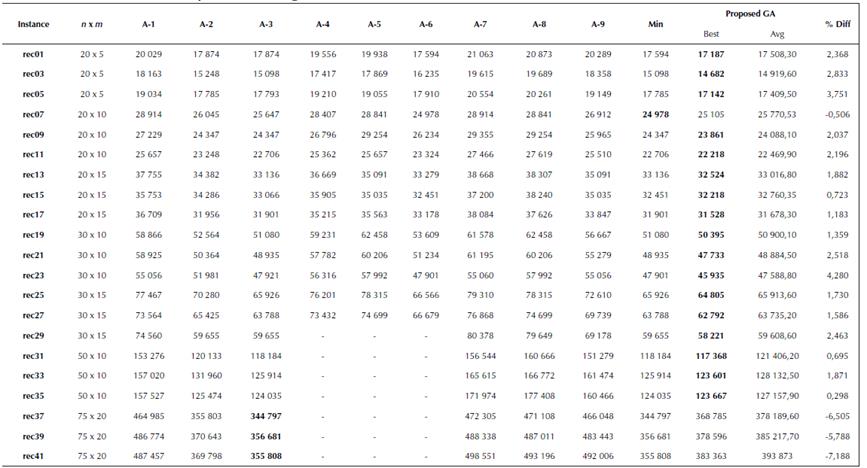
Problem set 2 consists of twenty-one problem instances adapted from Reeves (1995), ranging from 20-jobs 5-machines to 75-jobs 20-machines. Apart from the algorithms mentioned for Problem Set 1, the performance of the proposed algorithm was also compared with three more algorithms, as mentioned below:
A-7: Harmony search algorithm (Gao et al., 2010)
A-8: Differential evolution algorithm (Gao et al., 2010)
A-9: Grouping harmony search algorithm (Gao et al., 2010)
Comparative results of the proposed approach with nine other algorithms, i.e. from A-1 to A-9, for minimisation of total flowtime are given in Table 3. From Table 3, we can see that the proposed approach produced better results for 17 instances out of a total of 21. The proposed approach could not find better results for instance 'rec07', where the percentage error was 0,506%, as compared to the best-known value, i.e. to algorithm A-6. Furthermore, the performance of the proposed approach was also worse for problem size 75 χ 20, i.e. instances rec37, rec39 and rec41, where the percentage errors were 6,505%, 5,788% and 7,188%, respectively, compared to the best-known value among algorithms A1 to A-9. Only for algorithms A-2 and A-3, the results were superior to the proposed approach for problem size 75 χ 20. For all other problems, the results obtained by the proposed approach were superior to all other nine algorithms (A-1 to A-9). The best values found for each instance by various algorithms is marked in bold.
Table 3 Total flowtime comparison for algorithms A-1 to A-9 for Reeves (1995) data set
Source: Authors
Problem Set 3
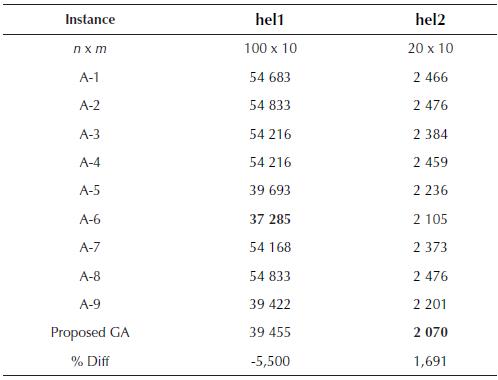
Problem set 3 consists of two problem instances adapted from Heller (1960). The first problem instance is a large sized problem with 100 jobs and 10 machines, while the second instance is a small sized problem with 20 jobs and 10 machines. For Problem Set 3, comparison of the GA was also done with nine algorithms (A-1 to A-9), as mentioned previously. The proposed GA was able to find superior results compared to all nine previous algorithms for problem instance 20 χ 10, while the performance was worse only in algorithms A6 and A9 for problem instance 100 χ 10. The comparative total flowtime values are presented in Table 4. The best values for each of the two instances are marked in bold.
Table 4 Tomtal flowtime comparison for algorithms A-1 to A-9 for Heller (1960) data set
Source: Authors
Problem Set 4
Problem set 4 consists of sixty problem instances adapted from Taillard (1993). mThe set consists of six subsets of problems with n x m combination of 20 χ 5, 20 χ 10, 20 χ 20, 50 χ 5, 50 χ 10 and 50 χ 20. Each set consists of 10 instances. The following heuristics were used for the comparison of results with the proposed GA algorithm:
A-10: Improved std dev heuristic proposed by Gao et al. (2011a)
A-11 : Job insertion based heuristic algorithm proposed by Bertolissi (2000)
A-12: Constructive heuristic, based on the idea of job insertion, proposed by Laha et al. (2008)
A-13: Heuristic algorithms proposed by Aldowaisan et al. (2004)
A-14: ISDH algorithm with local search by Gao et al. (2013)
A-15: IBH with local search algorithm by Gao et al. (2013)
A-16: ISDH algorithm with an iteration operator by Gao et al. (2013))
A-17: IBH algorithm with iteration operator by Gao et al. (2013)
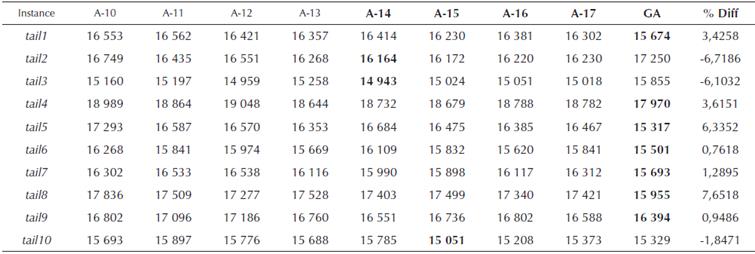
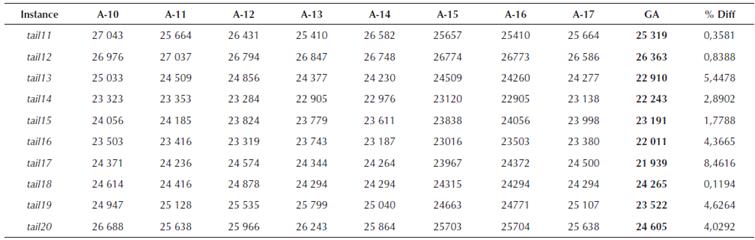
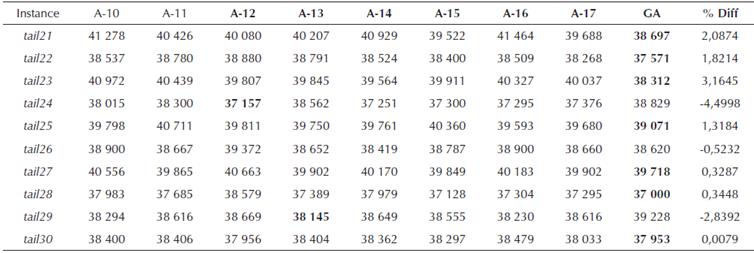
Table 5 to Table 10 give the comparative results for the total flowtimes found by various algorithms for the flow shop instances proposed by Taillard (1993). The best values among all instances are marked in bold.
Table 5 Total flowtime comparison for algorithms A-10 to A-17 for 20 x 5 data set from (Taillard, 1993)
Source: Authors
Table 6 Total flowtime comparison for algorithms A-10 to A-17 for 20 x 10 data set from (Taillard, 1993)
Source: Authors
Table 7 Total flowtime comparison for algorithms A-10 to A-17 for 20 x 20 data set from (Taillard, 1993)
Source: Authors
Table 8 Total flowtime comparison for algorithms A-10 to A-17 for 50 x 5 data set from (Taillard, 1 993)
Source: Authors
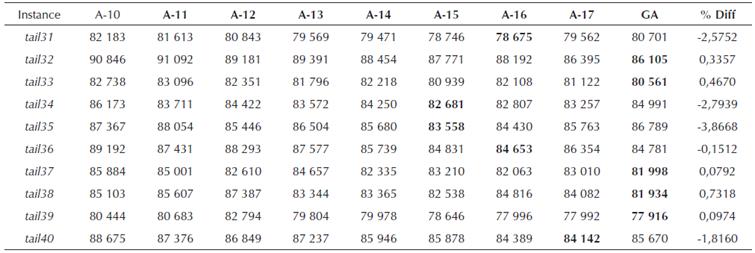
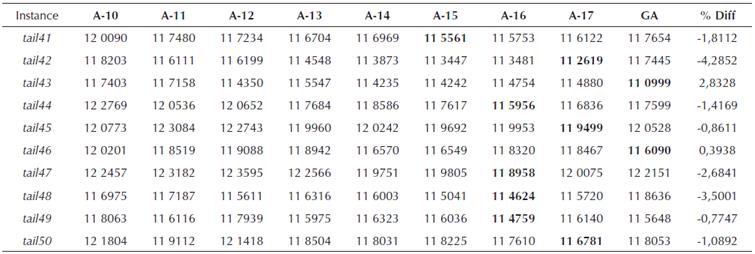
Table 9 Total flowtime comparison for algorithms A-10 to A-17 for 50 x 10 data set from (Taillard, 1 993)
Source: Authors
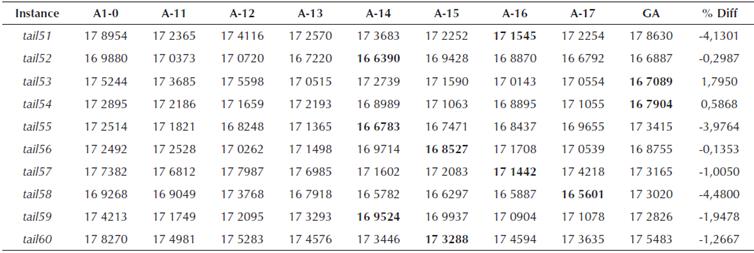
Table 10 Total flowtime comparison for algorithms A-10 to A-17 for 50 x 20 data set from (Taillard, 1993)
Source: Authors
From the preceding tables, we can see that the proposed GA approach was able to find better solution for 33 instances out of a total of 60 problem instances solved, while for 27 instances the performance was worse. For smaller size problems, i.e. for n = 20 (total of 30 instances), the proposed GA approach produced superior results for 24 instances, while worse only for six instances. For only two problem instances, i.e. tail2 and tail3, the %Diff between the proposed approach and the best solution by earlier approaches was more than 6%, while for the rest of the four problems the %Diff was 1,85%, 4,50%, 0,52% and 2,84% for problem instances tail10, tail24, tail26 and tail29, respectively.
As mentioned earlier, the performance worsened for large sized problem instances. For n = 50, a total of 30 instances were solved, but the GA found a better solution only for 9 of them. However, for the 21 instances where proposed GA approach was not able to find a better solution than the best solution value among earlier approaches, the maximum %Diff was less than 5% with maximum %Diff being 4,48%. It may be noted here that the best value found by the proposed GA algorithm was not worse than all the previous algorithms under discussion. The proposed approach did find better solution compared to some of the earlier algorithms.
Although the proposed approach was not able to find better solutions for all the instances, the performance of the algorithm can be considered robust. The general-purpose nature and the ability to handle any objective function without changing the basic GA routine makes it a truly general purpose scheduling approach. Furthermore, arrangement of data and schedule in familiar spreadsheet environment also makes it easy to use in shop floor environment. The general-purpose nature and robustness of the algorithm to address a large number of problems has been the key advantage of the proposed approach.
Conclusions
In this paper, a no-wait flow shop scheduling problem was considered where the objective was to minimise total flowtime. The problem has practical applications in process industries and is considered to be NP-hard even for 3-machine cases (Hans, 1984).
Though the performance of the proposed approach though was inferior in some cases, it found solutions that were equal or better than those of previous studies in a wide range of problems. The empirical analysis shows that the proposed approach can solve large sized flow shop problems with reasonable accuracy. The %Diff was calculated between the solution found by the proposed approach and the best value among all the previous solution techniques. For problem set 1, the proposed GA found better solution for six instances out of eight problem instances, while the same solution for the remaining two. For problem set 2, out of twenty-one instances, the proposed approach found better solutions for 17 instances and worse for four of them with maximum % Diff less than 10%. Problem set 3 consisted of only two problems. The proposed approach found a better solution for the small-sized problem, while for large-sized problem the % Diff was 5,50%. For problem set 4, the proposed approach found better solutions for 33 instances out of sixty problems and worse for the remaining 27 with a maximum % Diff of 6,72%. It may be noted here that the best value found by the proposed GA algorithm was not worse to all the previous algorithms under discussion. The proposed approach did find better solution compared to some of the earlier algorithms.
It was demonstrated that the proposed algorithm is simple to implement and easily customisable to include additional jobs or machines. The proposed GA approach has been implemented in a familiar spreadsheet interface and has the ability to generate Gantt chart, thus presenting a graphical representation of the schedules which is easily understandable by shop floor managers.