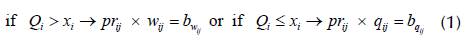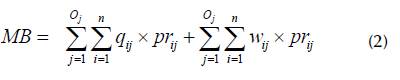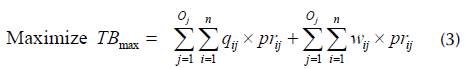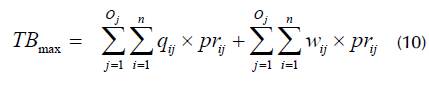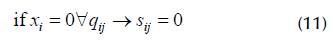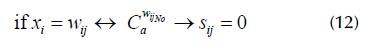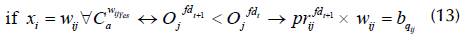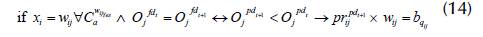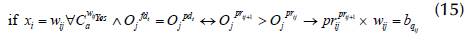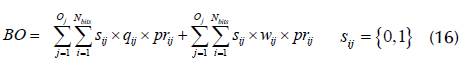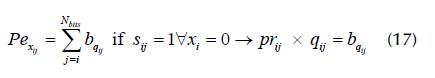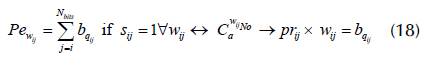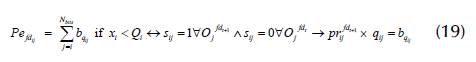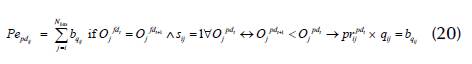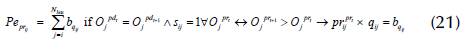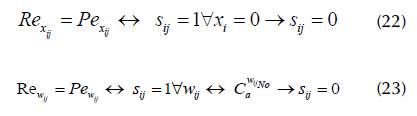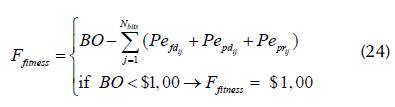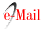Introduction
During the last decades, most companies have started to aim for large production and distribution volumes focusing on reducing lead times and inventory (van den Berg and Zijm, 1999; Richards, 2011; Haq and Boddu, 2017). The majority of customers, according to Pinto and Nagano (2020), have reduced the size of their orders and started to place them in shorter time intervals and minimum amounts of multiple Stock Keeping Units (SKUs) in their Distribution Centers (DCs). This tendency has resulted in shorter order fulfilment deadlines, and, consequently, it has started to demand greater process agility in DCs (Seyedrezaei et al., 2012; Matthews and Visagie, 2013; Marchet et al., 2015). The fact is that there are still no tools that can foresee the exact demand volume for dynamic stochastic environments in an unequivocal way (Seyedrezaei et al., 2012; Sereshti and Bijari, 2013; Baud-Lavigne et al., 2014). The option to maintain minimum levels in uncertain scenarios can cause, at a given billing moment, some SKU restrictions in the DC (Pinto et al., 2018). Additionally, most customers do not accept billings or receiving partial purchases, for example, in the e-commerce sector (Rim and Park, 2008). This fault will result in conflicting orders and the need to determine billing and fulfilment rankings for these SKUs (Rim and Park, 2008; Slotnick, 2011; Seyedrezaei et al., 2012; Huang and Ke, 2017; Ledari et al., 2018; Leung et al., 2018; Boysen et al., 2019; Pinto and Nagano, 2020). In this sense, this paper adresses a specific decision-making problem to maximize billing, which is called Optimized Billing Sequencing (OBS). This problem was initially approached by Pinto et al. (2018) and refers to the optimization of the billing processes of the order portfolio in a typical DC. In practice, OBS problems are usually very complex, and the pressure to maximize results and meet delivery deadlines demands agility in finding the best solution. However, dealing with a set of rules, restrictions, and decision variables without the help of a suitable quantitative tool becomes a complex task when the objective is to optimize the OBS. Fast decision-making based solely on experience or feeling may lead to waste of time and financial losses in the DC (Pinto et al., 2018). The literature, however, is insufficient and does not provide optimization methods (OMs) that can arrive at time and quality solutions that are satisfactory to all OBS instances. The available research neglects important practical aspects or offers lengthy solutions that constitute limitations for DCs. Therefore, there is a demand for OMs that are more robust and suited for the reality of DCs, which basically consist of achieving two OBS targets: OM robustness and practical application in DCs. Thus, this paper focusses on adapting to real world demands in order to deal with practical dilemmas not yet addressed by the OMs proposed for OBS. The entire OBS configuration under study is the same as the one considered by Pinto and Nagano (2020). In this sense, the amount of available inventory for billing is always controlled at minimum levels based on SKU demands. There are therefore some uncertainties regarding the management of the demand, which is stochastic, and billings occur based on Variable Time Windows (VTW). Most delivery deadlines are tighter, and there is a high frequency of small orders containing minimum amounts of multiple SKUs. Billing decisions prioritize order fulfilment and payment dates by the Earliest Due Date (EDD) rule. The proposed approach aims to enable managers to make decisions in a more agile and consistent way regarding the trade-off between the level of customer service and the financial result maximization of the aforementioned DCs. Thus, the objective of this paper is to provide an efficient billing maximization algorithm that, in an agile and consistent manner, produces optimized solutions for higher levels of OBS complexity. This algorithm is called Iterative Greedy Algorithm (IGA-OBS), and its performance is compared to the genetic algorithm (GA-OBS) by Pinto and Nagano (2020). In technical terms, the latter is an extension and improvement of the first GA-OBS that was proposed in the literature by Pinto et al. (2018), whereas, in methodological terms, this is a quantitative research based on mathematical modeling and computational simulation. Performance evaluations of the IGA-OBS in this work are carried out by means of intense computational experiments for a set of problems with different OBS complexity levels.
We have focused our attention on the potential of IGA-OBS/ GA-OBS for practical effectiveness and their capacity to adapt to the reality of current DCs. This paper is structured as follows: section 2 explains the OBS problem; section 3 presents the Literature review; section 4 expresses the model formulation of the OBS; section 5 presents the IGA-OBS; section 6 demonstrates the GA-OBS; section 7 brings the computational experiments and the performance assessments of the GA-OBS and the IGA-OBS; finally, the last section states the final considerations and the main suggestions for future studies and approaches to the OBS.
OBS problem
This section presents the OBS problem to maximize the billing of a typical DC. In this OBS, there are uncertainties regarding the management of the demand, which is stochastic, and SKU inventories available for billing are controlled at minimum levels in the DC. It is common for customers to place more than one order simultaneously, which constitutes a dynamic (online) input in the order portfolio regardless of SKU availability. These orders may have varied sizes and different quantities, or distinct unit selling prices for multiple combinations of different SKUs or of the same SKU. Most customers demand tighter delivery deadlines for a set of orders with multiple fulfilment and payment dates for a given VTW. Billing sequences are determined by analyzing the best combinations between fulfilment and payment dates, which are always prioritized by the EDD rule. All billings are generated after a certain number of orders accumulates in the order portfolio, which also occurs within time intervals pre-set by the VTW. Demands with partial inventory restrictions are billed according to costumer approval, and those referring to total restrictions are billed when the SKUs are available. Every order that is not billed due to SKU restrictions is transferred to the following VTW until the quantities of the mentioned SKUs are available in the DC. Therefore, the OBS problem is caused by restrictions or management failures resulting from the dynamics of changes, uncertainties, and disorders, in addition the pressing emergency in the reality of current DCs (Pinto et al., 2018). Decisions are usually made based on fulfillment rankings pre-defined by internal policies, which include a set of rules, constraints, and decision variables inherent to the OBS. In the literature, the mechanism to determine which SKUs are billed for each order was classified by Pinto et al. (2018) as a variation of the Knapsack Problem (KP). Thus, the OBS may be reduced to a decision-making problem, for which the ideal solution is to maximize the total billing of the order portfolio (Pinto and Nagano, 2020).
Literature Review
The available literature shows the research by Pinto et al. (2018) to be the first to approach and propose an OM for a specific problem of the so-called OBS. This OM is formulated through a hybrid GA, whose structure is based on the canonic GA by Holland (1975) and programmed in Visual Basic for Applications (VBA) from Microsoft Office Excel 2013. The hybrid GA is called GA-OBS, and it is formulated by means of binary genetic structures that use an elitist selection and an aptitude function guided by penalties and repairs of individuals that are unfeasible to the OBS. This GA-OBS can deal with inventory restrictions and with customer acceptance criteria regarding billings of partial amounts of SKUs to attribute them in an optimized manner to the order portfolio demand in compliance with the First Come, First Served (FCFS) rule. Experiments demonstrated that the proposed GA-OBS provides solutions that optimize billing and expedite decision-making processes for the OBS.
More recently, an important innovation that aims to provide approaches to OBS that are better adapted to real-world needs was proposed by Pinto and Nagano (2020). This approach proposes an extension and enhancement of the OBS by Pinto et al. (2018), along with the Optimized Picking Sequence (OPS) by Pinto and Nagano (2019). These problems refer to the optimization of billing and manual picking processes, respectively, in a typical parts Warehouse (WA). The WA in question operates with a picking system that fits into the low-level picker-to-parts category with pick-and-sort process, and it has only one area known as Pick-up and Drop-off (P/D). The research objective was to provide a OM that integrated and offered optimized solutions for OBS/OPS in order to better deal with the trade-off between the level of customer service and the efficiency of said WA. The proposed OM was formulated by integrating two Gas called GA-OBS and GA-OPS. GA-OBS deals with inventory restrictions and possible partial billings, maximizes the total order portfolio billing by prioritizing the fulfilment and payment dates in compliance with the Earliest Due Date (EDD) rule, and generates a picking order for the GA-OPS. In the sequence, GA-OPS, which comprises the iteration of batch (GABATCH) and routing (GATSP) algorithms to satisfy all specificities of the problem and to minimize picking total time and cost for the OPS. Programming was done in Python, and both data inputs/outputs and results analyses were supported by Microsoft Office Excel 2016. Experiments with problems with different complexity levels showed that the proposed tool produces solutions of satisfactory quality and speeds up decision-making and operational processes so as to optimize financial results and productivity of the WAs.
Evidently, GA applications stand out for their robustness, implementation, and hybridization flexibility with other OMs (Gen et al., 2008; Bottani et al., 2012). However, Pinto et al. (2018) applied the GA-OBS to solve only one single-size problem, and they did not include large OBS instances. The objective of the authors' approach was to gain insights into the best population size configuration and number of generations linked to variations in the genetic operator parameters that can maximize the solution potential of the GA-OBS. Therefore, the authors themselves recognize the need for tests in problems of higher instances, as well as the implementation of other parameters, operators, and genetic representations or evolutionary designs that can improve performance. In Pinto and Nagano (2020), the proposal was to address the integration of problems by considering a series of practical dilemmas present in WAs. The solutions are of satisfactory quality for different instances and complexity levels configured for the OBS/OPS. However, solutions for problems in large instances demand considerable efforts in terms of checking and repairing chromosomes to be performed by GAs. These occurrences may result in an exponential increase of computational processing time and make the OM inefficient for some WAs.
Similar approaches to the OBS that presuppose inventory restrictions and uncertainties associated to the demand forecast were proposed by Rim and Park (2008) and Seyedrezaei et al. (2012). Rim and Park (2008) used the entire binary Linear Programming (LP) to deal with inventory restrictions in order to fulfil DC orders, aiming to maximize the Order Fill Rate (OFR). SKUs are only attributed to orders if there is available inventory in the DC; if there is not, orders are transferred to the next day and fulfilled according to SKU availability and priority rules to avoid excessive delays to the OFR. Experiments demonstrated that LP is better than the simple models in terms of order size and/or number of SKUs when compared to the FCFS rule. Seyedrezaei et al. (2012) applied the GA to a NP-complete inventory forecast and demand problem to plan and maximize the number of orders fulfilled according to Customer Importance, SKU Useful Life, and Back-Orders. This GA calculates the demand coefficient of each customer for a given time period and defines an inventory considering the DC's capacity and the useful life of the SKUs. Hence, orders that are not fulfilled due to SKU restrictions are transported to the next period (back-order). Compared to the Lingo software, the GA arrived at solutions with higher quality and satisfactory time to better manage DCs. In the search for more robust strategies and optimization methods, advanced technologies for intelligent decision making in manufacturing and logistics are presented by Chien et al. (2012). Other approaches focused on producing solutions that can maximize costs and/or maximize order fulfilment profit in an agile and flexible manner are found in high-impact journals (Ghiami et al., 2013; Mousavi et al., 2013; Bandyopadhyay and Bhattacharya, 2014; Diabat, 2014; Park and Kyung, 2014; Diabat and Deskoores, 2016; Kumar et al., 2016; Mousavi et al., 2017; Inkaya and Akansel, 2017).
Model formulation
In the OBS, the SKU notation refers to the registration number that distinguishes the n product types available in the DC stock. The quantity of each SKU in stock at a given t moment of the VTW is given by x, and it is represented by the set X = {x1, x2, xn}, in which the subscript i = (1, 2 n) denotes the i-th SKU. The Purchase Order Portfolio (POP) comprises n orders, represented by POP = {O1, O2, On}, and the subscript j refers to the j-th order ∀j = (1, 2, n). These orders are from a set of m customers, represented by CG = {C1, C2, Cm}, in which the subscript a = (1, 2, m) denotes the a-th customer (Cα) of the POP. The total demand of x in the POP is given by Q, whereas the demand of x j in O j is given by qij being O j = {q1j q2j,…, q nj } ∀i = (1, 2 n) attributes of C α . If TV is the Total Value of the POP at the t instant of billing in the VTW, then, the TV will only be obtained if xi ≥ Q i , in which y is the restriction of x i and w i = (Qi - y i ) is the availability of x in case y > 0. Thus, the notationcy-' determines that the customer accepts w billing to O j , whereas cw α determines that the customer does not accept w billing to O j .. The insertion date of q ij in the POP is denoted by id., and, subsequently, the pre-defined priority criteria for the OBS are obtained: i) fd - order fulfilment date of i in O j ii) pd. - order payment date of i in O j and; iii) pr.. - unit selling price of i in O j . The entire billing process of is carried out by comparing Q i . to the offer of x, so that, every non-billed qij will be transferred to t+1 to be processed again by the next VTW. Up next are the indexes, parameters and restrictions, as well as the decision criteria and variables that configure the OBS optimization problem:
• Parameters and restrictions
VTW: Variable Time Windows;
t: VTW billing moment;
O j : refers to the j-th order of the POP in t;
C a : refers to the a-th customer of the POP in t;
q ij : SKU demand in the O of the POP in t;
Q i : total demand of a SkU of the POP in t;
xi: total number of a SKU in the DC in t;
yi: restriction of x in the DC regarding the Q. of the
POP in t;
wi: partial availability of x (Qi - yi) in the DC in case yi > 0 in t.
• Decision criteria and variables
pr..: SKU unit price in the O j ;
fd ij : SKU fulfillment date in the O j ;
pd ij : SKU payment date in the O j ;
C α wijYes : determines if C accepts billings of w i to O j ;
C α wijNo : determines if C a does not accept billings of w i to O j .
OBS optimization is subjected to the calculation of the possible Maximum Billing (MB) that can be obtained from the inventory of each SKU available in the DC versus the Q. of the POP at a given t moment of the VTW. The calculation of the MB is then used to check the need for execution and of an IGA-OBS/GA-OBS search parameter to optimize the OBS. In cases where the MB < TV, i.e. if xi < Q i , so the MB will be the main parameter of the best possible solution for the OBS. The calculation criterion to obtain the MB, as demonstrated by Equation (1), prioritizes the highest pr ij according to the following parameters: i) b wij . - billing value of w ij and; ii) b qij - billing value of q ij .
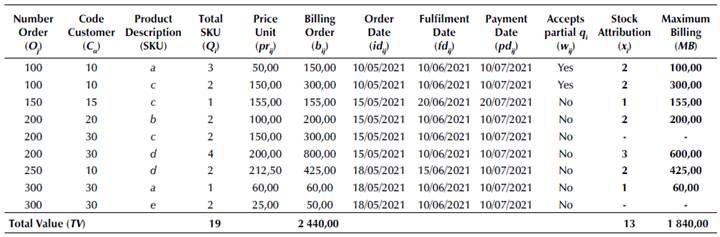
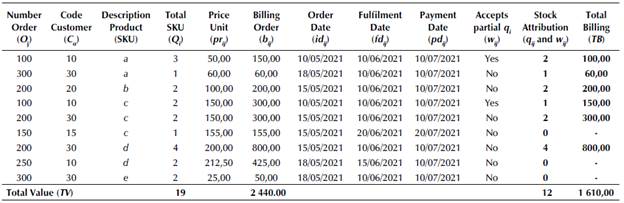
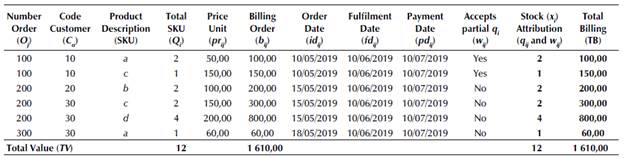
Then, MB can be obtained according to Equation (2). In the sequence, Table 1 demonstrates a calculation example of the MB for a given POP. In this example, we presuppose that the CD's inventory volume is represented by X = {3a, 5 b , 3 c , 5d, 0e, 1f, 0 g and 5h}.
Table 1 shows that, given the availability of x i , and prioritizing only the highest pr ij according to b wij and b qij , the algorithm found the best billing mix, i.e., MB = 1 840,00, then, MB < TV (xi < Qi). For example, for "d", despite fdd200 < fdd250, the algorithm prioritized billing for O250, given that, prd250 > prd200 in POP. Note that the MB does not yet consider all the criteria and decision variables inherent to the OBS. Therefore, Total Billing (TB) maximization of the POP can be expressed as a mathematical programming model to maximize TB max : 1. If x = 0, s.. = 0 according to Equation (11).
Billing (TB) maximization of the POP can be expressed as a mathematical programming model to maximize TB max :
Subjected to:
The objective function in Equation (3) is to find the maximum possible billing of the POP. Restriction (4) ensures that q i will only be attributed to O if, in a t given moment of the VTW, the variable x i > 0 in the DC. Restriction (5) ensures that, ∀C α wijNo , the total demand of qij can only be attributed to its corresponding O j if, at a t given moment of VTW, the variable xi ≥ q ij in the DC. Restriction (6) will make sure that a given w can only be attributed to O j if w i > 0 in the POP and c α wijYes . Variables (7), (8), and (9) determine that the rules for fd ij , pd ij , and pr. are satisfied in the POP.
Iterative Greedy Algorithm (IGA-OBS)
The logic of the IGA-OBS is based on the verification and attribution technique through the iteration of a set of interdependent elements which configure the OBS. The first phase of its formulation is the sorting mechanism of the POP by the fulfilment priority levels defined by fd ij /pd ij / pr ij . It is assumed that fd ij and pd ij have respectively higher priority levels than the pr ij of the POP. Hence, q ij and w ij are attributed by automatically comparing and updating inventory balances after each SKU attribution. Therefore, q ij or w is attributed to O. by the variable s ij . Thus, = qi or wi; otherwise, s ij = 0 to obtain the TB maximization according to Equation (10).
Thus, q i or w i may or may not be attributed to the j-th depending on parameters and restrictions, decision criteria, and variables inherent to the OBS. The attribution routine verifies whether there is a balance of x i in the DC, and, after each execution, the IGA-OBS produces a solution that maximizes the TB of the POP. q i or w i to O j is attributed according to the following conditions:
1. If x i = 0, s ij = 0 according to Equation (11).
2. If x i = w ij in case C α wijNo , s ij = 0 according to Equation (12).
3. If fdt+1 < fdt, fdt+1 is prioritized over fd t according to Equation (13).
4. If pdt+1 < pdt, pdt+1 has preference over pd t according to Equation (14).
5. If pr ij+1 > pr ij , pr ij+1 is prioritized over pr.. according to Equation (15).
To exemplify the solution of the problem given by Table 1, Table 2 shows how the IGA-OBS performs both the POP ordering and the assignments of x i to maximize TB. The following colors are used to demonstrate the attributions of q i and w ij in order to exemplify the calculation that maximizes TB: i) black: it refers to the total attributions of qij ii) green: it corresponds to the attributions of wij and iii) red: it indicates the q ij and w ij that were not attributed due to the total restrictions of a given SKU.
On Table 2, it can be observed that, for "α", O 100 and O 300 have identical fd ij and pd ij . However, pr > pr a300 > pr a100 and, if O100 has C α wijYes as a criterion for billings of w ij , s i100 = 2α and s i300 = 1α. Note that for “c”, O 150, even having the highest pr c among the orders, is discarded because fd 150 is higher than fd 100 and fd 200. In case of “d”, there is insufficient inventory of x d to satisfy O 200 and O 250, and both have C α wijNo Cα as a criterion for billings of w ij . Thus, if fd 200 < fd 250, the option is to satisfy O 200. As for “e”, there were no attributions as x d = 0, that is, the entire IGA-OBS solution logic satisfies all demands inherent to the OBS to maximize the TB. Table 3 presents the list of q ij to be billed, whereas the q ij that will not be billed is represented by y = {1 a , 2 c , 2 d and 2 e } due to y i restrictions. In sequence, Algorithm 1 shows the IGAOBS pseudocode
Genetic algorithm (GA-OBS)
In the evolutive genetic structure of the GA-OBS, the representation of chromosome (C) is given by a binary string {0,1}, which attributes q. or w to O by variable s ij = 1 ; otherwise, s ij = 0. Then, a C is divided into O n genes, and q ij or w ij is an allele of the j-th gene according to Figure 1.
The population is a matrix denoted by N pop , with N bits being the number of bits of C, and N ger the total of generations in the exécution of the GA-OBS (Haupt, R. and Haupt, S., 2004). The initial N pop is generated randomly (Man et al., 1996), i.e., if s.. < 0,5, s ij = 0 ; otherwise, s ij = 1, and N bits is equal to the number of POP lines. Therefore, the Billing Obtained (BO) by C is given by Equation (16).
The fitness function (Ffitness) first penalizes every C that is not feasible to the OBS by assigning a negative value equal to the b qij of the invalid bit, in which ∀s ij = 1 according to the following conditions: If s ij = 1 and xi = 0: penalty Pe x is imposed according to Equation (17).
1. If s ij =1 to w ij in case :Cα wijNo: penalty Pe w is imposed according to Equation (18).
2. The s ij = 1 must prioritize the first fd ij in the POP: If xi < Q i , fd t is preferred over fdt+1 ; otherwise, penalty Pe fd is imposed according to Equation (19).
3. The s ij = 1 must prioritize the first pd ij , in the POP: after checking the fd ij , if pdt+1 < pdt, pdt+1 is prioritized; otherwise, penalty Pe pd is imposed according to Equation (20).
4. The s ij = 1 must prioritize the highest pr ij in the POP: after checking the fd ij and the pd ij , if pr ij + 1 > pr ij , pr ij +1 is prioritized; otherwise, penalty Pe pr is imposed according to Equation (21).
Next, F fitness makes repairs by swapping "l" for "0" in bits with incidence of Pe x and Pe w by means of Re and Re repairs according to Equations (22) and (23).
Therefore, b qij , and b wij , for N bits repaired are $0,00, and $1,00 is attributed to F fitness in case F fitness < 1, i.e., F fitness may vary from $0,00 to BO according to Equation (24).
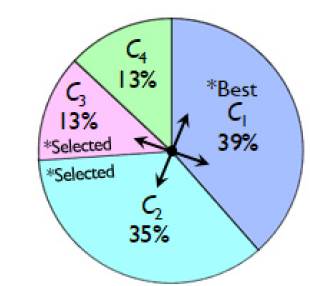
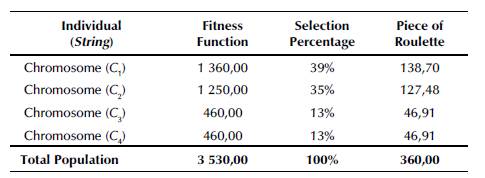
The roulette wheel by Holland (1975), linked to Elitism (E) by De Jong (1988), is used as a selection technique, in which only the best C (C Elite ) of each Nger is transferred to become the first C of N ger+1 . The selection probability of each individual is equivalent to a certain slice of the roulette wheel, as expressed by Equation (25).
To exemplify this, Table 4 shows the calculus of the selection probability for four individuals. Then, the select graphic by the roulette wheel with elitism is demonstrated by Figure 2.
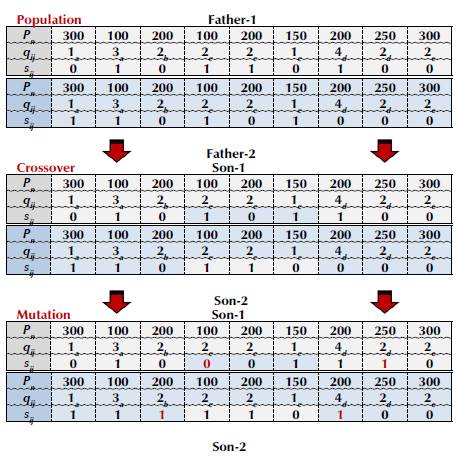
The implemented crossover operator is of the two-point kind, and the mutation is an adaptation of the flip type, both by Holland (1975). Figure 3 illustrates the crossover and mutation diagram implemented to GA-OBS.
Figure 3 shows that the crossover is applied to the "Parents" according to the crossover probability (p c ) pre-defined for the GA-OBS. In the crossover, each O j and q ij remain static, while permutations occur only for s ij in order to form the "Sons" of N ger+1 Figure 3 also shows that the mutation affects the "Sons" resulting from the crossover, and it will be applied according to the mutation probability (pm), whereas t x is the rate for the exchange between the N bits of C. Therefore, each bit to be mutated is randomly chosen and receives a value corresponding to the exchange between 0 and 1 for the s ij of C. Note that the mutated bits (red) make changes in the genetic pattern of the "Sons".
Thereupon, pc, pm, and t x allow a parameterization that can vary from 0 to 100%. However, after being pre-defined, they remain fixed during all the N ger in each execution of the GA-OBS. To generate Npop+1 the N pop swapping technique with elitism by De Jong (1988) is used. The termination criterion used, prevailing the first one obtained, is that the MB or N ger is used. Algorithm 2 shows the GA-OBS pseudocode.
Computational experiments and result analyses
This section and its subsections detail problem configurations, computational experiments, and analyses of the results obtained by the GA-OBS and the IGA-OBS.
These analyses focused on assessing performance and on the conditions to adapt GA-OBS/IGA-OBS to the reality of the aforementioned DC. Algorithm implementations and computational experiments were carried out in a microcomputer featuring a 2.0GHz i7 processor and 8GB of RAM. Programming was conducted in Python, and both data inputs/outputs and analyses were supported by Microsoft Office Excel 2016. Experiments included a set of problems with different complexity levels based on the literature and the reality of DCs. The entire problem conigurations and the instances used in the experiments are identical to those considered by Pinto and Nagano (2020). Therefore, the problems are classified into three categories: i) Small (SM); ii) Medium (ME) and; iii) Large (LG).
Test probjems and parameter setting
This subsection details problem formulations and parameter configurations or each OBS category. For a better comparative analysis of the algorithms, all the problems are conigured so that the MB is the optimized solution for the OBS. Thus, in the DC under study, there is a total of 1 250 types of SKUs to satisfy the POP at a given t moment of the VTW. Depending on the OBS category, SKU restrictions in the DC are the following: i) xi = 0 from 1 to 2,5% and; ii) xi = 2 from 2 to 3%. All billing processes take place immediately after VTW = 8 (hours), where 50% of the POP orders contain C α wijYes and fr Yes . The number of SKUs that repeat among the n orders of each POP range from 50 to 80%. However: i) if x i . = 0, there will be no SKU repeated in another order; ii) if x i = 2, there will be only one SKU repeated in another order. Date conigurations are shown next, and they presuppose that t refers to the date of the last order input in the POP. For idij: i) 50% have id ij = t; and ii) 50% of the remaining id ij range from id ij = t-5 days to id ij = t-1 days. For fdij: i) 30% (fdij = t); ii) 30% (fdij = t+10 days); iii) 20% (fdij= t+20 days); and iv) 20% (fdij= t+30 days). For pdij: i) 20% (pdij = t); ii) 20% (pdij = t+10 days); iii) 20% (pdij= t+15 days);iv) 20% (pdij= t+30 days); and v) 20% (pd, = t+45 days). pr ij is randomly determined by an even distribution function [100, 1 000]. However: i) if x = 0, pr ij = $200,00; ii) if x = 2, pr ij = $100,00; and iii) if SKU repeated among orders is C α wijNo , then pr ij = $ 120,00. Table 5 summarizes the problems formulated for the OBS.
Computational results and analyses
This section describes the results of the computational experiments and the performance analyses of the GA-OBS/ IGA-OBS proposed for the OBS. The analyses were carried out by means of Outcome Assessment Metrics (OAM), and the final assessment was consubstantiated by the set of average results obtained by the GA-OBS/IGA-OBS. GA-OBS computational experiments demonstrated that a critical factor in the generation of high-aptitude inviduals is the calibration of the genetic operators. There is no standard formula to indicate which ideal parameter configuration will produce the appearance of C Elite in the GA-OBS. While considering that the new generations are not deterministic, we sought to better deal with the trade-off between the quality of the solutions and the computational efficacy of the GA-OBS. The option was to use average parameters that better adjusted to the real situations and the design of the evolutive genetic structure of the GA-OBS. After the execution series for the each OBS problem category, combinations and parameter minimum and maximum limits that provided the best solutions to the GA-OBS are summarized in Table 6.
In Table 6, it is possible to verify that the initial N pop ranges from 200 to 2 000 individuals, and that the N ger ranges from 200 to 12 000 individuals. Notice that p c ranges from 50 to 80%, while p m ranges from 20 to 80% using a t x of 1 or 2% depending on OBS complexity. Tables 7 and 8 sumarize the results obtained by the GA-OBS and IGA-OBS according to the following OAM: i) Tardiness in Customer Orders (TCO); ii) Number of Fulilled Orders (NFO); iii) Total of Billed Products (TBP); iv) Computational Processing Time (CPT); v) Maximum Billing (MB) ; and vi) Total Billing (TB).
Tables 7 and 8 demonstrate that GA-OBS and IGA-OBS can satisfy all rules, restrictions, and decision criteria to maximize the TB for each OBS instance. The genetic structure implemented in the GA-OBS can conduct the search for C Elite , and meet al conditions attributed to the OBS. In general, the GA-OBS converges up to C Elite from the third until the tenth generation at most for each OBS category. This demonstrates that the size of both the N pop and the N ger and that pc, pm, and t x have proved to be sufficient to create a level of diversity capable of capturing all OBS specificities and allow the convergence of the GA-OBS.
However, obtaining the best results for instances of higher OBS levels is conditioned to significant increases in the size of the N pop and the N ger . Thus, there is a relative dependence on the size of the N pop and the N ger , which, if they are not large enough to expand the search space, will make the GA-OBS stagnate in a local solution that is distant from TB maximization. Note that, for a POP with more than 30 orders containing more than 80 lines and 200 SKUs, the GA-OBS obtained a much higher CPT than the IGA-OBS.
This happens because the GA-OBS solutions require an exaustive search for a large number of possible solutions, thus demanding intensive effort in verifications and repairs, which exponentially expands the CPT and can make it unfeasible for OBS reality. Probabilistic properties and the configuration of the genetic representation linked to an aptitude function guided by penalties and repairs are critical factors for the evolution and convergence of the GA-OBS. We also verified that the GA-OBS is extremely sensitive to the calibration of genetic operators and the parameterization of pc, pm, and tx, which is the best possible to favor the diffusion of positive genetic features for each new generation of the GA-OBS. Improper parameterizations can destroy the aptitude of the individuals or force the evolution to occur more slowly, as well as leading to a premature convergence or demanding a CPT that makes the GA-OBS unfeasible. The fact is that, the greater the OBS instance, the greater the number of penalties and repairs, thus the longer the GA-OBS solution will be.
In practical terms, the GA-OBS is limited to medium-size problems and differs from the needs of managers when faced with the complexities present in the daily reality of DCs. On the other hand, the experiments evidenced that the performance of the IGA-OBS was much better than that of the GA-OBS, and that it produced optimized solutions with a CPT that is less than one minute for any OBS category. The use of the IGA-OBS enables managers to deal more quickly and consistently with higher levels of OBS complexity; the faster the flow of information, the higher is the degree of negotiation accuracy, and the faster is the OBS decision-making. These actions result in less waste of time and greater flexibility and precision to schedule billing and picking processes within the DC. IGA-OBS solutions optimize the quality of order protfolio fulilment and cash flow management by reducing the DC's eventual financial losses. In general terms, the IGA-OBS provides a tool that enables managers to make decisions in a more agile and consistent way regarding the trade-off between the level of customer service and the maximization of the DC's financial result. In addition to that, the IGA-OBS does not use penalties or repairs, and it can be implemented without major difficulties to other OBS and DC configurations. The option to use Excel allows the main current management software programs to extract .xls files to make uploads to the IGA-OBS. Analysis of SKU inventory specificities and the best VTW adjustment regarding the POP size also contribute to formulating OMs with practical designs that are more robust and suitable for OBS.
Final considerations
This paper proposes an efficient algorithm to solve a specific billing maximization problem called Optimized Billing Sequencing (OBS). Initially approached by Pinto et al. (2018), OBS refers to the optimization of order portfolio billing processes in a typical Distribution Center (DC). In the OBS under study, Stock Keeping Unit (SKU) inventories are controlled at mimimum levels inside the DC. There are, however, uncertainties regarding the management of the demand, which is stochastic, and billings occur from Variable Time Windows (VTW). Most delivery deadlines are tight, and there is a high frequency of small orders containing minimum amounts of multiple SKUs. It is not uncommon that, when billing, determining fulilment rankings may be necessary, as well as analyzing whether customers accept partial amounts due to SKU restrictions. Decision making about billing prioritizes fulfilment and payment dates in compliance with the Earliest Due Date (EDD) rule. Thus, the new algorithm proposed for the OBS was called Iterative Greedy Algorithm (IGA-OBS) and its performance was compared to the genetic algorithm (GA-OBS) by Pinto and Nagano (2020). Experiments with problems with different levels of complexity demonstrated that the algorithms satisfy all rules, restrictions, and decision variables, and they obtain solutions of satisfactory quality for all OBS instances. It was evidenced that the GA-OBS is limited to medium-size problems, as it demands a high computational processing time that differs from those required to the reality of current DCs. However, the GA-OBS is capable of producing optimized solutions with a computational processing time of less than one minute for any OBS problem. This research fills a gap in the literature and makes valuable contributions to further studies on the development of algorithms with practical designs that are more robust and suitable for OBS. The proposed IGA-OBS enables managers to make decisions in a more agile and consistent way in terms of the trade-off between the level of customer service and the maximization of the financial result of the aforementioned DC. There is still a vast field of inquiries and assumptions for new optimization methods for many other approaches and configurations for the so-called OBS. The main limitation is that the literature does not yet provide an available database with different OBS problems to better test the IGA-OBS/GA-OBS. Suggestions for further researches are: i) to conduct studies with actual applications, so a comparative analysis of the processes adopted by managers versus those resulting from the IGA-OBS can be made; ii) to implement more efficient designs to elements, parameters, and genetic operators, or formulate evolutionary genetic representations that improve the GA-OBS performance; iii) to carry out extensive computational experiments by means of comparative studies among other renowned metaheuristics versus the IGA-OBS; iv) to assess the IGA-OBS with dynamic variables in order to deal with payment deadlines, cashflow, demand forecast, and production lead times that replenish DC inventories.