Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Colombiana de Cardiología
Print version ISSN 0120-5633
Rev. Colom. Cardiol. vol.17 no.2 Bogota Mar./Apr. 2010
(1) Grupo de investigación INSIGHT. Bogotá, Colombia.
(2) Cardiología pediátrica. Fundación Cardioinfantil. Bogotá. Colombia.
Centro de procedencia: Grupo de Investigación INSIGHT, Bogotá, Colombia. Proyecto n° 1868 financiado por el Banco de La República- Fundación Cardioinfantil.
Correspondencia: Javier O. Rodríguez-Velásquez. MD. Director del Grupo de investigación INSIGHT. Dirección: Cra 79B N° 51-16 Sur. Int. 5 Apto. 102, Barrio Kennedy, Bogotá, Colombia.Teléfono: 4527541. Correo electrónico: grupoinsight2025@yahoo.es.
Recibido: 09/02/2009. Aceptado: 20/11/2009.
Antecedentes y objetivos: la geometría permite la caracterización matemática objetiva de las formas; la geometría fractal caracteriza objetos irregulares. La forma de los estados dinámicos del ventrículo izquierdo que se observa mediante eco-cardiografía, puede evaluarse de manera objetiva a partir de medidas de dimensiones fractales.
Métodos: se midió la dimensión fractal a través del método de Box-Counting de tres objetos definidos en 28 imágenes eco-cardiográficas, 16 de infantes normales (grupo A) y 12 enfermos (grupo B), a fin de establecer diferencias entre salud y estados patológicos a partir de su comparación con las dimensiones fractales de dos prototipos de normalidad y dos de enfermedad.
Resultados: se desarrolló una nueva metodología diagnóstica de aplicación clínica basada en el concepto de "armonía matemática intrínseca", y se halló que las dimensiones fractales de los objetos definidos para un ecocardiograma enfermo presentan similitudes hasta en su cuarta cifra significativa, con lo que se evidencia la posibilidad de seguir la evolución de normalidad a enfermedad. De acuerdo con los cálculos realizados 68,75% de los casos del grupo A podrían tener mejor evaluación con el diagnóstico desarrollado y los enfermos podrían diagnosticarse de modo más efectivo.
Conclusiones: las imágenes ecocardiográficas pediátricas pueden caracterizarse de manera objetiva con medidas de dimensión fractal, lo cual permite desarrollar una metodología de diagnóstico clínico de la eco-cardiografía en menores de edad, a partir del concepto de armonía matemática intrínseca.
PALABRAS CLAVE: ecocardiografía, fractal, armonía matemática intrínseca.
Background and objectives: Geometry allows the objective mathematical characterization of forms. Fractal geometry characterizes irregular objects. The left ventricle dynamical states form observed through echocardiography can be objectively evaluated through fractal dimension measures.
Methods: A measurement of fractal dimension was performed using the Box-counting method of three defined objects in 28 echocardiographic images, 16 from normal children (group A) and 12 ill children (group B), in order to establish differences between health and illness from its comparison with the fractal dimensions of 2 normality prototypes and 2 disease prototypes.
Results: A new diagnostic, clinical application methodology was developed based in the "intrinsic mathematical harmony" (IMH) concept, and it was observed that the fractal dimensions of the defined objects for an abnormal echocardiogram show similarity to its fourth significant number, thus demonstrating the possibility of following up the evolution from normality towards disease. According to the performed calculations, 68.75% of the cases in group A could be better evaluated with the developed diagnostic methodology, and the ill ones could be diagnosed more effectively.
Conclusions: The pediatric echocardiography images can be objectively characterized with fractal dimension measurements, thus enabling the development of a clinical diagnostic methodology of echocardiography in children from the IMH concept.
KEY WORDS: echocardiography, fractals, intrinsic mathematical harmony.
Introducción
La geometría es una rama de la matemática que estudia las propiedades de las figuras en el espacio. La geometría euclidiana clásica se aplica a las superficies planas, mientras que las no euclidianas se aplican a las superficies curvas o a objetos irregulares (1, 2). La aplicación de medidas euclidianas en objetos irregulares observados en modelos de experimentación en animales, se utiliza en el desarrollo de métodos de evaluación de diferentes exámenes; sin embargo, en la mayoría de los casos sus resultados dependen de la subjetividad y experiencia del observador (3). La utilización de nuevas formas de medición basadas en geometría fractal (4, 5) ha producido resultados exitosos en la descripción de la morfología y fisiología animal y humana a nivel experimental y clínico (6-11).
En cardiología, Huikuri y colaboradores (12) proporcionaron medidas predictivas de mortalidad después de infarto agudo del miocardio a partir de medidas fractales. Goldberger y colaboradores (13) asociaron enfermedad a comportamientos excesivamente periódicos o aleatorios, mientras que una conducta intermedia se asoció con la salud, desarrollando así la concepción salud/enfermedad de los sistemas dinámicos. Su reinterpretación permitió el desarrollo de un nuevo método de diagnóstico matemático objetivo y reproducible de la monitoría fetal mediante la aplicación de la ley de Zipf/Mandelbrot (14). Rodríguez y colaboradores establecieron conceptos como el de armonía matemática intrínseca (15), variabilidad y diferencia neta (16), que evidencian discrepancias matemáticas entre normalidad y enfermedad a partir de análisis geométricos de los objetos estudiados, ya que las dimensiones fractales analizadas de forma aislada pueden resultar insuficientes para realizar diagnósticos clínicos.
La ecocardiografía es uno de los procedimientos diagnósticos de mayor uso en la evaluación del funcionamiento cardiaco por su bajo costo y su carácter no invasivo. Para su evaluación se han desarrollado medidas con base en geometría euclidiana, que aproximan su forma a la de una estructura regular (17, 18), lo cual hace que los diagnósticos sean dependientes de la subjetividad y experiencia del observador, y dificulten el establecimiento de diagnósticos precisos y reproducibles.
El objetivo de este trabajo es desarrollar una metodología geométrica para la caracterización matemática objetiva del ecocardiograma pediátrico, a través de la medición de las dimensiones fractales de imágenes en sístole y diástole que se calculan con el método de Box-Counting y se evalúan mediante el concepto de armonía matemática intrínseca. La metodología desarrollada permitirá la evaluación simultánea de la estructura ventricular izquierda en sístole y diástole, estableciendo un parámetro matemático de diferenciación objetiva y reproducible, entre normalidad y enfermedad, aplicable en la clínica.
Métodos
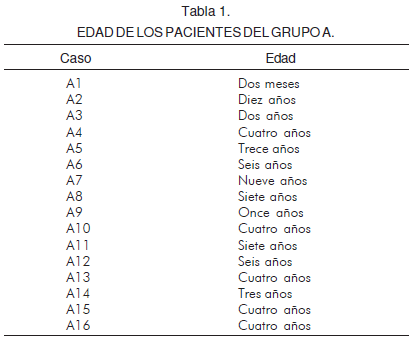
Se tomaron 28 ecocardiografías de pacientes con edades entre diez días de nacidos a diecisiete años de edad, clasificados y agrupados según el diagnóstico clínico convencional realizado por un médico experto. Los exámenes se clasificaron en dos grupos: el grupo A corresponde a menores normales, dieciséis pacientes, y los menores del grupo B presentan afecciones cardiacas, de los cuales doce resultaron representativos de enfermedad (Tablas 1 y 2).
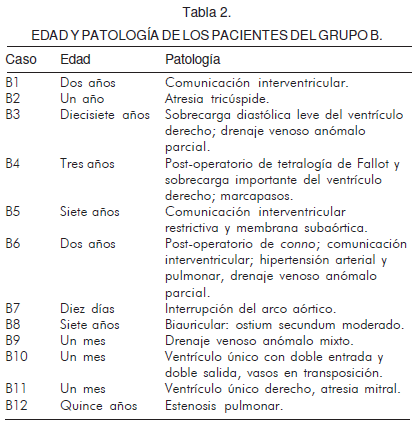
Como prototipos de normalidad y enfermedad, se eligieron cuatro ecocardiogramas los cuales no presentaron dudas en su diagnóstico tanto desde los parámetros clínicos convencionales de análisis del ecocardiograma como desde la evaluación clínica general; el primer ecocardiograma escogido como prototipo de enfermedad presentó estenosis pulmonar, mientras el segundo ventrículo único con doble entrada y doble salida, además de vasos en transposición.
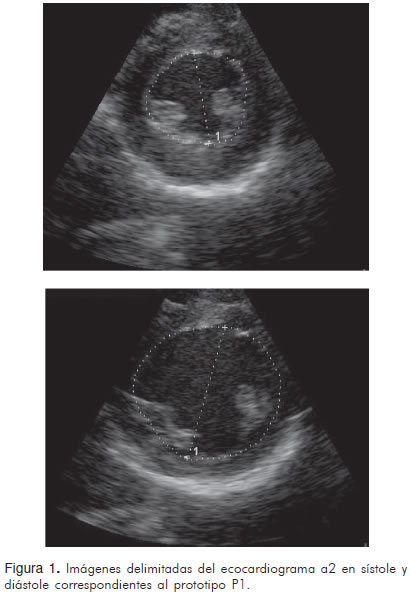
El examen ecocardiográfico se realizó con un equipo VIVID 3 de General Electric®, del servicio de eco-cardiografía pediátrica de la Fundación Cardioinfantil; con éste se tomaron las imágenes y se realizó la delimitación de los objetos observados con el procedimiento convencional realizado por un experto (Figura 1).
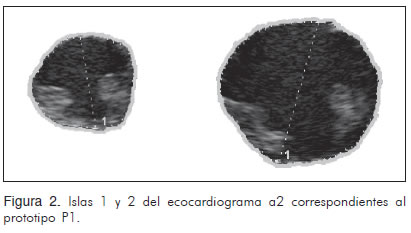
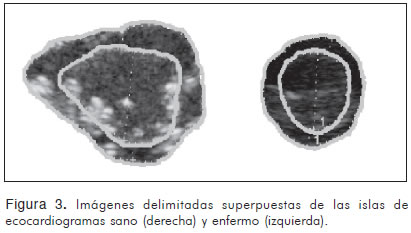
Los contornos ecocardiográficos del ventrículo izquierdo en diástole y sístole se denominaron isla 1 e isla 2 respectivamente. Adicionalmente se desarrolló el concepto de isla total, correspondiente a la unión de las islas 1 y 2. Las islas fueron aisladas de la imagen total de la eco-cardiografía (Figura 2) y se les superpusieron cinco rejillas con cuadros de 10 - 5 - 2,5 - 1,2 y 0,6 milímetros de lado, realizando el respectivo conteo de cuadros para la obtención de la dimensión fractal a través del método de Box-Counting (Figura 3).
Análisis matemático
La evaluación de las ecocardiografías se hizo mediante el cálculo los valores numéricos de las dimensiones fractales calculadas en las dos islas y la totalidad (ver definiciones).
Las dimensiones fractales de las islas en los cuatro prototipos fueron evaluadas con el concepto de armonía matemática intrínseca. Posteriormente estas medidas se contrastaron con las dimensiones fractales de las ecocardiografías de ambos grupos en busca de características matemáticas de diferenciación entre normalidad y enfermedad.
Dado que esta metodología se basa en procedimientos matemáticos generales para la caracterización de la dinámica cardiaca, las medidas que se obtienen caracterizan matemáticamente cada caso particular sin necesidad de hacer análisis estadísticos sobre una población específica.
Definiciones
Fractal: del latín fractus, interrumpido. Objeto irregular. Término que se define como sustantivo: objeto irregular, y como adjetivo: irregularidad.
Dimensión fractal: medida numérica adimensional del grado de irregularidad de un fractal. La definición de dimensión fractal usada en este trabajo es la dimensión fractal de Box-Counting.
Dimensión fractal de Box-Counting:
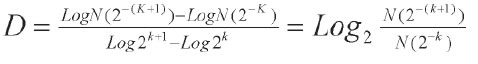
donde:
N: número de cuadros que contiene el contorno del objeto.
K: grado de partición de la cuadrícula.
D: dimensión fractal.
Armonía matemática intrínseca: grado de similitud o diferencia entre las unidades y las cifras significativas de las dimensiones fractales de las islas. Cuando la diferencia en las dimensiones fractales está en la unidad se denota con cero, cuando es en la primera cifra significativa con uno, en la segunda con dos y en la tercera con tres*.
Isla 1: objeto que se obtiene de la imagen ecocardiográfica de acuerdo con el contorno en diástole delimitado por el experto.
Isla 2: objeto que se obtiene de la imagen ecocardiográfica de acuerdo con el contorno en sístole delimitado por el experto.
Isla total: objeto matemático constituido por la unión de las islas 1 y 2.
Prototipos normales: imágenes ecocardiográficas sin dudas en su diagnóstico normal denominados P1 y P2.
Prototipos enfermos: imágenes ecocardiográficas con patologías severas, sin dudas en su diagnóstico, denominados P3 y P4.
Resultados
Las dimensiones fractales del grupo A están entre 0,8856 y 1,1483 para la isla 1, entre 0,0117 y 1,1074 para la 2 y entre 0,9136 y 1,1047 para la total, mientras que los valores del grupo B están entre 0,9304 y 1,0153 para la isla 1, entre 0,9250 y 0,9884 para la 2 y entre 0,9298 y 0,9943 para la total.
Los rangos en que se encuentran las dimensiones fractales para cada isla, no diferencian los grupos, lo que muestra que las dimensiones fractales aisladas no son un parámetro para caracterizar los grupos.
Al evaluar las dimensiones fractales calculadas para las islas dinámicas en los cuatro prototipos seleccionados, con el concepto de armonía matemática intrínseca, se encontró que un paciente es normal cuando los grados de irregularidad difieren sólo en su primera cifra significativa, mínimo en una de las tres comparaciones. Por ejemplo, el prototipo 2, (Tabla 3), presenta un valor de 1 en las dos primeras relaciones y 2 en la relación de la isla 2 con la total. El paciente A11 presenta 1 en la última relación y en las demás relaciones el valor es 0, por lo cual se considera normal desde esta metodología (Tabla 4).
En contraste, los pacientes enfermos se caracterizan porque sus dimensiones fractales difieren en la segunda, tercera y cuarta cifra significativa, pero no presentan diferencia en la primera cifra significativa en ninguna de las tres comparaciones. Por ejemplo, el prototipo 4 (Tabla 3) presenta valores de 2 en todas las relaciones y el paciente B1 presenta valores de 4 en todas las relaciones, por lo cual se considera enfermo (Tabla 5).
Posiblemente son enfermos o están en evolución hacia la enfermedad quienes, como en los casos de los pacientes A5 y B9, en las relaciones entre isla 1 y 2 e isla 1 y total, presentan un valor de 0 y en la última relación se encuentra un valor de 2. Para este tipo de casos se recomienda un seguimiento cuidadoso a fin de observar su evolución en el tiempo.
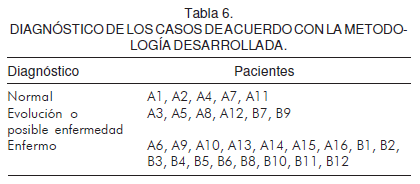
En las tablas 4 y 5 se comparan las dimensiones fractales de las islas uno y dos, uno y total, y dos y total. La tabla 6 presenta el diagnóstico de los casos de acuerdo con la metodología desarrollada.
Discusión
Este es el primer trabajo en el que se evalúa matemáticamente el ecocardiograma pediátrico a través de la medición de la dimensión fractal de imágenes en sístole y diástole. Se aplicó el concepto de armonía matemática intrínseca al desarrollo de una nueva metodología diagnóstica, estableciendo un parámetro de diferenciación objetiva, reproducible y aplicable en la clínica. La metodología desarrollada permite la evaluación simultánea de la estructura ventricular izquierda en sístole y diástole, encontrando que las dimensiones fractales establecen diferencias matemáticas entre normalidad y enfermedad. Los ecocardiogramas cuya evaluación de armonía matemática intrínseca es 1 en cualesquiera de las relaciones establecidas por las islas, se asocian a normalidad, mientras que los que presentan los valores de 2, 3 y 4 en la armonía matemática intrínseca en más de una de las relaciones sin un valor 1 como mínimo, se asocian con enfermedad. Los casos en los que la relación entre las islas 1 y 2, y entre las islas 1 y total tengan un valor igual a 0, y la relación entre la isla 2 y la total presente un valor igual a 2, posiblemente están asociados a enfermedad o a evolución hacia ésta y se recomienda un seguimiento posterior cuidadoso.
Los prototipos escogidos permiten la determinación de las características matemáticas fundamentales que diferencian normalidad de enfermedad, a partir de las cuales se realiza una evaluación del resto de casos. Esta metodología diagnóstica evalúa cada caso de manera objetiva a partir de sus características geométricas, independientemente de la patología específica y de la edad del paciente, siempre y cuando sea menor de dieciocho años, encontrando medidas numéricas generales del estado de normalidad o enfermedad del ventrículo izquierdo que hacen innecesario el uso de métodos estadísticos. Así, al comparar órdenes de magnitud utilizando la función exponencial en base e, por ser ésta la función inversa a la función logaritmo, se encuentra que el grado de similitud entre las partes y la totalidad, en los pacientes normales, oscila en órdenes entre e0=1 ye1=2.178; mientras que en los enfermos se encuentra entre e10=22026.4658 y e1000=1,97x10434, es decir que el grado de similitud entre las partes componentes y la totalidad en los casos enfermos llega incluso a ser 10434 veces mayor que en los casos normales.
Estudios previos evidencian que las alteraciones morfológicas se relacionan con anomalías funcionales; tal es el caso de las simulaciones de la actividad cardiaca realizadas por Kappenberger (19), quien muestra cómo la geometría y la anatomía influyen la estabilidad eléctrica del corazón. Esta es la razón por la cual el análisis geométrico del ventrículo, en dos momentos funcionales diferentes, puede dar cuenta de su estado de normalidad o enfermedad. La caracterización matemática permite superar el carácter descriptivo de los diagnósticos tradicionales, en los que sólo se consideran los estados de normalidad y enfermedad, así como su objetiva evolución. De acuerdo con la metodología desarrollada, 68,75% de los sujetos del grupo A corresponden a pacientes enfermos o en evolución hacia la enfermedad, al presentar órdenes matemáticos característicos de los prototipos de enfermedad. Este hecho evidenciaría dificultades en la objetividad del diagnóstico tradicional y la posibilidad de un análisis más objetivo por medio del diagnóstico desarrollado. Es necesario realizar estudios posteriores de esta metodología para su aplicación clínica a pacientes adultos, así como para evaluar el verdadero impacto clínico de la importancia de la evolución hacia la enfermedad. En la actualidad los pacientes diagnosticados como sanos desde la metodología vigente, no presentan dificultades posteriores.
De acuerdo con el tipo de eco-cardiografía realizada, el ventrículo se estudia a través de aproximaciones a distintas figuras regulares que no corresponden a lo que se observa en los modelos obtenidos de vaciados en cera (17, 18). El análisis aislado de las dimensiones fractales obtenidas para las islas 1 y 2 no permite establecer rangos de diferenciación entre normalidad y enfermedad. Mediante el concepto de armonía matemática intrínseca se construyó un objeto matemático abstracto denominado isla total, que da cuenta de la estructura ventricular en sístole y diástole de manera unificada y que es independiente de mayores o menores grados de irregularidad del ventrículo, basándose en la determinación matemática de relaciones armónicas que caracterizan al cuerpo humano.
La aplicación de conceptos matemáticos y físicos a la caracterización y el diagnóstico de la morfología y dinámica de diferentes sistemas biológicos, dio lugar a resultados efectivos en estudios clínicos y experimentales. Tal es el caso de los trabajos de Goldberger (20-22), basados en la teoría de los sistemas dinámicos, y los de Rodríguez y colaboradores, quienes desarrollaron un método de caracterización de radiografías de tórax con base en geometría fractal aplicada a casos normales (23) y patológicos (24), y evidenciaron un comportamiento fractal del repertorio inmune caracterizando el grado de complejidad del repertorio T específico contra al alergeno Poa p9 (25). Manivannan y colaboradores (26) realizaron medidas del ventrículo izquierdo en ecocardiogramas bidimensionales, desarrollando un índice geométrico denominado IE (índice de excentricidad) que permite evaluar la disfunción sistólica. Rodríguez y colaboradores (16), evaluaron la dinámica fractal de la ramificación coronaria izquierda de pacientes con presencia y ausencia de enfermedad arterial oclusiva severa, a partir de los conceptos de variabilidad y diferencia neta aplicados a imágenes consecutivas de sístole a diástole; de manera análoga, en este trabajo se utiliza una abstracción matemática, la isla total, para evaluar un mismo objeto en diferentes estados dinámicos. Estos trabajos evidencian que la superación de los problemas en el diagnóstico de exámenes médicos puede basarse en medidas objetivas y en concepciones físicas y matemáticas que permitan la interpretación diagnóstica de las medidas realizadas.
Aplicaciones futuras
Se desarrollará una generalización de esta metodología aplicándola a exámenes ecocardiográficos de adultos y se estudiarán las implicaciones pronosticas de la evolución entre normalidad y enfermedad. La automatización de éste y otros métodos de diagnóstico matemático de la estructura y dinámica cardiaca, permitirá el desarrollo de métodos de evaluación integrados de estos exámenes.
Conclusiones
Las imágenes ecocardiográficas pediátricas pueden caracterizarse de manera objetiva con medidas de dimensión fractal.
La construcción matemática de la isla total a partir del concepto de armonía matemática intrínseca, permite desarrollar una metodología de diagnóstico clínico de la ecocardiografía en menores de edad.
Medidas que tengan por lo menos una vez el valor 1, en alguna de las relaciones establecidas entre las islas, corresponden a un estado saludable, mientras que valores de armonía matemática intrínseca de 2, 3 o hasta 4, sin un valor 1 como mínimo, se asocian con enfermedad. Por último, son posiblemente enfermos o están en evolución hacia la enfermedad los casos en que las medidas de las relaciones de armonía matemática intrínseca entre la isla 1 y la 2, y entre la isla 1 y la total, tengan un valor igual a cero y la relación entre isla 2 y la total muestre un valor igual a dos, por lo que se recomienda un seguimiento cuidadoso en el tiempo.
Esta metodología diferencia clínicamente normalidad de enfermedad de manera matemática objetiva para cada caso individual, independientemente de la patología específica y de la edad del paciente, si éste es menor de dieciocho años.
El 68,75% de los casos del grupo A puede ser mejor diagnosticado con esta metodología que con la evaluación clínica tradicional.
Dedicatoria
Infinitas gracias a todos los maestros, en especial al Maestro de Maestros, que con su amor y bendiciones hizo que lo extraordinario abriera las puertas de nuestros corazones.
A los maestros Newton y Kepler, que con su ejemplo nos llevaron a apreciar la belleza y armonía del universo.
A los niños colombianos.
_______________
* Por ejemplo para el ecocardiograma A4, la dimensión fractal de la isla 1 es 0,8856 y la de la isla 2 es 0,9356, encontrando diferencia en la primera cifra significativa, es decir que la armonía matemática intrínseca entre estas islas es 1. En el ecocardiograma A8, la dimensión fractal de la isla 1 es 1,0096 y la de la isla 2 es de 0,9454, diferenciándose en la unidad, es decir que le corresponde el valor 0 de armonía matemática intrínseca. Para el ecocardiograma B4 la dimensión fractal de la isla 1 es 0,9465 y de la isla total 0,9422 diferenciándose en la tercera cifra significativa, es decir, un valor de armonía matemática intríseca de 3. REGRESAR
Agradecimientos
Este trabajo hace parte de los resultados del proyecto No. 1868 financiado por el Banco de la República, por lo cual agradecemos a esta entidad.
A la Fundación Cardioinfantil por el apoyo al desarrollo de esta investigación, especialmente al director de investigaciones, el Dr. John Dennis.
A Olga Pérez, enfermera de la Fundación Cardioinfantil, por su paciencia y apoyo en la consecución de las imágenes y la información.
Bibliografía
1. Somerville DM. The elements of non-eucliean geometry. New York: Dover Publications, 1958. [ Links ]
2. Mandelbrot B. Introducción. En: Los Objetos Fractales. Barcelona: Tusquets Eds. S.A.; 2000. p. 13-26. [ Links ]
3. Lafont A, Topol EJ. Experimental evidence of remodeling after angioplasty. En: Arterial remodeling: a critical factor in restenosis. Boston, Mass: Kluwer Academic Publishers; 1997. p. 51-68. [ Links ]
4. Mandelbrot B. The fractal geometry of nature. San Francisco: Freeman; 1972. p. 341-348. [ Links ]
5. Peitgen H, Jurgens H, Saupe D. Chaos and fractals; new frontiers of science. New York: Springer; 1992. p. 183-228. [ Links ]
6. Glenny RW, Robertson HT, Yamashiro S, Bassingthwaighte JB. Applications of fractal analysis to physiology. J Appl Physiol 1991; 70: 2351-67. [ Links ]
7. Burgos J. Fractal representation of the immune B cell repertoire. Biosystems 1996; 39: 19-24. [ Links ]
8. Burgos J, Moreno-Tovar P. Zipf-scaling behavior in the immune system. Biosystems 1996; 39: 227-32. [ Links ]
9. Arle JE. Simon, Richard H. An application of fractal dimension to the detection of transients in the electroencephalogram. Electroencephalogr Clin Neurophysiol 1990; 75: 296-305. [ Links ]
10. Kiselev VG, Hahn KR, Auer DP. Is the brain cortex a fractal? Neuroimage 2003; 20 (3): 1765-74. [ Links ]
11. Cheng SC; Huang YM. A novel approach to diagnose diabetes based on the fractal characteristics of retinal images. IEEE Trans Inf Technol Biomed 2003; 7 (3): 163-70. [ Links ]
12. Huikuri HV, Makikallio TH, Peng Ch, Goldberger AL, Hintze U, Moller M. Fractal correlation properties of R-R interval dynamics and mortality in patients with depressed left ventricular function after an acute myocardial infartion. Circulation 2000; 101: 47-53. [ Links ]
13. Goldberger A, Amaral L, Hausdorff JM, Ivanov P, Peng Ch, Stanley HE. Fractal dynamics in physiology: alterations with disease and aging. PNAS 2002; 99: 2466-72. [ Links ]
14. Rodríguez J, Prieto S, Ortiz L, Bautista A, et al. Diagnóstico matemático de la monitoría fetal aplicando la ley de Zipf-Mandelbrot. Rev Fac Med Univ Nac Colomb. 2006; 54 (2): 96-107. [ Links ]
15. Rodríguez J, Mariño M, Avilán N, Echeverri D. Medidas fractales de arterias coronarias en un modelo experimental de reestenosis; Armonía matemática intrínseca de la estructura arterial. Rev Col Cardiol 2002; 10: 65-72. [ Links ]
16. Rodríguez J, Álvarez L, Mariño M, Avilán N, Prieto S, Casadiego E. et al. Variabilidad de la dimensión fractal del árbol coronario izquierdo en pacientes con enfermedad arterial oclusiva severa. Dinámica fractal de la ramificación coronaria. Rev Col Cardiol 2004; 11 (4): 185-92. [ Links ]
17. Muñoz R, Marcus E, Palacio G, Gauvreau K, Wessel DL, Colan SD. Reconstruction of 3-Dimensional right ventricular shape and volume from 3 orthogonal planes. J Am Soc Echocardiogr 2000; 13 (3): 177-185. [ Links ]
18. Marcus E, Muñoz R, Palacio G, Wessel D, Colan SD. A new quantitative method for the diagnosis of right ventricular hypertensive disorder in 3 dimensions. J Am Soc Echocardio 2000; 13: 186-193. [ Links ]
19. Kappenberger L. Arrythmia: a therapeutic dilemma. En: Computer Simulation and Experimental Assessment of Cardiac Electrophysiology. Lausanne: Futura Publishing Company; 2001. p. 185-8. [ Links ]
20. Goldberger A, Rigney D, West B. Chaos and fractals in human physiology. Sci Am 1990; 262: 42-9. [ Links ]
21. Goldberger A, West BJ. Fractals in physiology and medicine. Yale J Biol Med 1987; 60: 421-35. [ Links ]
22. Lipsitz L, Goldberger A. Loss of "complexity" and aging. (preliminary communication) JAMA 1992; 267 (13): 1806-1809. [ Links ]
23. Rodríguez J, Lemus J, Serrano J, Casadiego E, Correa C. Medidas fractales cardiotorácicas en radiografía de tórax. Rev Col Cardiol 2005; 12 (3): 129-34. [ Links ]
24. Rodríguez J, Prieto S, Correa C, Avilán N, Ulloa H, Caicedo R. Medidas fractales de radiografías de tórax de pacientes con diferentes patologías. Rev Cienc Salud 2006; 4 (1): 31-38. [ Links ]
25. Rodríguez J. Comportamiento fractal del repertorio T específico contra el alergeno Poa P9. Rev Fac Med Univ Nac Colomb 2005; 53 (2): 72-8. [ Links ]
26. Manivannan J, Reddy MR, Thanikachalam S, Kumar RA. Quantitative evaluation of left ventricle performance from two dimensional echo images. Echocardiography 2006; 23 (2): 87-92. [ Links ]














