Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Colombiana de Cardiología
Print version ISSN 0120-5633
Rev. Colom. Cardiol. vol.17 no.3 Bogota May/June 2010
Predicciones físicas y matemáticas de la dinámica cardiaca de aplicación clínica
Physical and mathematical predictions of the cardiac dynamic for clinical application
Grupo INSIGHT, Bogotá, Colombia.
Correspondencia: Dr. Javier Rodríguez. Cra. 79 B N° 51-16 Sur. Int. 5 Apto. 102, Barrio Kennedy, Teléfono: 3134057252. Bogotá, DC., Cundinamarca, Colombia. Correo electrónico: grupoinsight2025@yahoo.es.
Recibido: 20/07/2009. Aceptado: 21/12/2009.
ANTECEDENTES: la teoría de sistemas dinámicos cuantifica los estados y la evolución de los sistemas. La cuantificación de espacios de ocupación de atractores caóticos en el espacio de fases partiendo del Holter, diferenció un grupo de enfermedad aguda de otro normal y con enfermedad crónica.
OBJETIVO: crear una nueva metodología de ayuda diagnóstica para la dinámica cardiaca cuantificando los sistemas dinámicos con probabilidad y entropía.
MÉTODO: se desarrolló una inducción con diez Holters construyendo atractores en el mapa de retardo y cuantificando pares ordenados de la frecuencia cardiaca durante dieciocho horas, evaluando la probabilidad de ocupación, entropía y sus proporciones para tres regiones de los atractores, buscando valores predictivos de normalidad-anormalidad.
Las predicciones se confirmaron con veinte casos. Se enmascararon conclusiones del Holter y antecedentes clínicos en una muestra de treinta pacientes, sobre la cual se aplicó la metodología físico-matemática; así mismo se desenmascararon los resultados clínicos, calculando sensibilidad, especificidad y coeficiente Kappa respecto al diagnóstico físico-matemático.
RESULTADOS: se diferenciaron dinámicas cardiacas agudas, crónicas, normales y evolución normalidad-enfermedad; con las proporciones de la entropía de los atractores. Se desarrolló una metodología predictiva de ayuda diagnóstica clínica para el Holter. La confirmación de las predicciones con los veinte casos, acertó en 100%; la sensibilidad y especificidad fueron de 100%. La concordancia entre el «estándar de oro» y el diagnóstico físico-matemático fue de 1.
CONCLUSIONES: la dinámica cardiaca evaluada con las proporciones de la entropía, reveló una auto-organización acausal predecible del atractor dinámico geométrico, que constituye un método de ayuda diagnóstica aplicable a la clínica.
PALABRAS CLAVE: Holter, atractor caótico, probabilidad, entropía.
BACKGROUND: the dynamic systems theory quantifies the states and evolution of systems. Quantification of the chaotic attractor occupation spaces in the phases space based on the Holter, differentiated a group of acute disease from another normal group and with chronic disease.
OBJECTIVE: to create a new methodology of diagnostic aid for the cardiac dynamics quantifying the dynamics systems with probability and entropy.
METHOD: an induction with ten Holter monitors was developed; building attractors in the space of phases and quantifying ordered pairs of the heart rate during 18 hours, evaluating the occupation probability, entropy and entropy's proportions for 3 attractor's regions, looking for predictive normality/disease values.
The predictions were confirmed in 20 cases. The conclusions of the Holter and the clinical antecedents in a 30 patients sample to which a physical/mathematical methodology was applied, were covered; likewise, clinical results were uncovered, quantifying sensibility, specificity and Kappa coefficient with regard to the physical/mathematical diagnosis.
RESULTS: the acute, chronic and normal cardiac dynamics and the normality/sickness evolution were differentiated by the quantification of the proportions of entropy attractors. A predictive clinical diagnostic aid methodology for the Holter evaluation was developed. Confirmation of predictions in the 20 cases was 100% successful, as was sensibility and specificity. The concordance between the Gold-standard and the physical/mathematical diagnosis was equal to 1.
CONCLUSIONS: the cardiac dynamics evaluated by the entropy proportions revealed an acausal and predictable self-organization of the geometric dynamic attractor, that constitutes an aid diagnostic method for clinical use.
KEY WORDS: Holter, chaotic attractor, probability, entropy.
Introducción
La teoría de los sistemas dinámicos caracteriza los estados y la evolución de los sistemas por medio de representaciones de sus variables dinámicas en el espacio de fases. De manera general, se presentan tres diferentes clases de atractores, los cuales corresponden a dinámicas predecibles e impredecibles, estos son: el punto, el ciclo y el caótico (1); la dimensión fractal es una medida que puede cuantificar la irregularidad de los atractores caóticos (2). Los fractales, de forma habitual, se pueden dividir en tres clases: abstractos (3, 4), salvajes (4) y estadísticos (5); el uso de medidas fractales ha permitido la cuantificación y evaluación de varios sistemas morfológicos y fisiológicos (6-9).
La teoría de los sistemas dinámicos ha sido aplicada para la caracterización de diversos sistemas fisiológicos, como la dinámica cardiaca fetal (10) y de adultos (11); en un trabajo desarrollado por Rodríguez y colaboradores se estudió la dinámica cardiaca en el Holter y se desarrolló una caracterización objetiva que diferencia dos grupos: el primero enfermedad aguda y el segundo casos normales y con enfermedad crónica (12).
El Holter es una prueba de electrocardiografía ambulatoria, de tipo no invasivo, que evalúa dos o tres canales electrocardiográficos durante un período de 24 a 48 horas, y permite determinar cambios dinámicos de los fenómenos eléctricos que son de corta duración y transitorios. Se desarrolló con el objetivo de obtener mayor información sobre la variación del funcionamiento cardiaco; su mayor utilidad es la detección de arritmias, así como la evaluación de cambios del segmento ST -isquemia-, cambios en los intervalos R-R variabilidad de la frecuencia cardiaca-, y diagnóstico y valoración de arritmias cardiacas. Es muy usado para la evaluación de la respuesta a tratamientos (13).
La probabilidad es una medida matemática de los posibles eventos de un experimento que se evalúa por medio de una fracción entre la frecuencia de aparición de cada evento y los eventos totales. El espacio abstracto que contiene a todos los eventos se denomina espacio muestral; esta medida cuantifica la posibilidad de la existencia futura de cada evento (14).
Las teorías que surgen para resolver el problema de muchos cuerpos del orden de 1023 (15) son la termodinámica y la mecánica estadística, constituyentes de la primera de tres revoluciones científicas que, junto con la mecánica cuántica y los sistemas dinámicos construyeron para la física una concepción acausal del orden de la naturaleza. El concepto de entropía fue enunciado por Carnot e históricamente ha sido reinterpretado en los contextos de la teoría cinética de los gases, la mecánica estadística y la teoría de la información (16-18).
El algoritmo de la entropía aproximada, publicado en 1991 (19) básicamente se desarrolló para cuantificar la regularidad de las señales biológicas en la presencia de un ruido blanco; esta medida cuantifica la predecibilidad de valores futuros para la amplitud del electroencefalograma (EEG) basado en el conocimiento previo de las amplitudes (20), cuantificando qué tanto los patrones de datos se repiten a sí mismos en límites predeterminados de tolerancia sobre la siguiente comparación de incrementos (21, 22). Cuanto menor sea el valor de la entropía aproximada menor es la complejidad o impredecibilidad de la serie de datos. Aunque la entropía aproximada puede calcularse a partir de grupos de datos pequeños, la cantidad de datos tiene una influencia en el valor del resultado (23).
Experimentos con sujetos normales no muestran cambios significativos en la entropía aproximada de las fluctuaciones de la frecuencia cardiaca después de la administración de atropina, lo cual sugiere que el tono vagal no es un determinante de la entropía aproximada (24, 25). Esta misma medida ha aumentado durante ejercicio después del nivel umbral ventilatorio y durante ejercicio después de atropina, manteniendo el concepto de que las activaciones simpáticas aumentan la entropía aproximada (25). Observaciones en pacientes con fallas cardiacas congestivas avanzadas, sugieren que el tratamiento con beta-bloqueadores no altera los valores de la entropía aproximada (26). Se ha encontrado que valores reducidos de la entropía aproximada en las fluctuaciones de latidos cardiacos preceden episodios espontáneos de fibrilación atrial en pacientes sin enfermedad cardiaca estructural (27); además los valores de entropía aproximada antes del comienzo de la fibrilación atrial fueron menores en comparación con los valores obtenidos del grupo control de sujetos normales. El incremento de la predictibilidad en el comportamiento de la frecuencia cardiaca, medida con la entropía aproximada, también precede episodios espontáneos de fibrilación atrial después de cirugía de bypass de las arterias coronarias (28). Aunque se ha asociado reducción en la complejidad de la dinámica cardiaca con complicaciones post-operatorias de cirugía vascular, no hay evidencia clara de que cambios en la complejidad del comportamiento de la frecuencia cardiaca se relacionen con riesgos de muerte (29).
El propósito de la investigación es diseñar una nueva metodología de ayuda diagnóstica para la dinámica cardiaca a partir del Holter, basada en la teoría de la probabilidad y la entropía, cuantificando las proporciones de la entropía de los pares ordenados de la frecuencia cardiaca del atractor en el espacio de fases.
Definiciones
Mapa de retardo: tipo de atractor específico que representa de manera gráfica la dinámica de un sistema, ubicando pares ordenados de valores de una variable dinámica consecutiva en el tiempo en un espacio de dos o más dimensiones.
Par ordenado de frecuencias cardiacas: se define como cualquier combinación consecutiva de dos frecuencias cardiacas representadas como (x,y) las cuales estarán contenidas en el mapa de retardo, ubicándose en el rango de cinco correspondiente de acuerdo con sus coordenadas.
Probabilidad de pares ordenados consecutivos en rangos de cinco: se define como el cociente entre la cantidad de pares ordenados que ocupen dicho rango y el total de pares ordenados de todo el trazado (14).

Donde: X, Y son múltiplos de 5.
Entropía del atractor: en un sistema no equiprobable, como en el caso de los rangos de (X,Y) la entropía de la ocupación de un atractor en el espacio de fases está dada por:
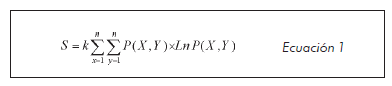
Donde: X, Y son múltiplos de 5, P(X, Y) es la probabilidad para el rango (X, Y), k es igual a la constante de Boltzmann, 1,38 x 10-23 (J/k) y S el valor de la entropía (16, 17).
Proporción S/k del atractor: al despejar de la ecuación 1, se obtiene el valor para la proporción S/k en función de la suma de las probabilidades por sus logaritmos naturales.
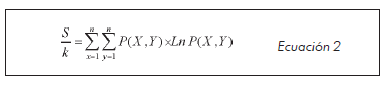
la cual puede re-escribirse así:
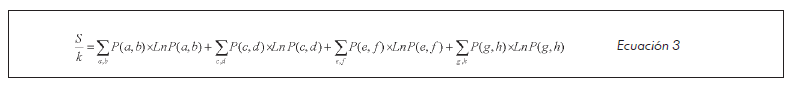
Donde a, b, c, d, e, f, g, h son múltiplos de 5 latidos por minuto, P(a,b) es la probabilidad para los rangos que corresponden a frecuencias de ocupación de unidades, P(c,d) es la probabilidad para los rangos que corresponden a frecuencias de ocupación de decenas, P(e,f) es la probabilidad para los rangos que corresponden a frecuencias de ocupación de centenas, P(g,h) es la probabilidad para los rangos que corresponden a frecuencias de ocupación de miles, k es igual a la constante de Boltzmann, 1,38 x 10-23 (J/k) y S el valor de la entropía (16, 17).
Para finalmente simplificar la anterior ecuación en la siguiente expresión:
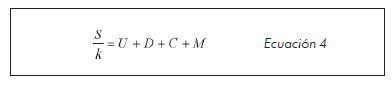
Donde U es la suma que corresponde a las frecuencias de ocupación de unidades, D es la suma que corresponde a frecuencias de ocupación de decenas, C es la suma que corresponde a frecuencias de ocupación de centenas, M es la suma que corresponde a frecuencias de ocupación de miles, k es igual a la constante de Boltzmann, 1,38 x 10-23 (J/k) y S el valor de la entropía (16, 17).
Proporciones: divisiones entre las sumas (partes componentes de la totalidad que corresponde a la proporción S/k) de las frecuencias de ocupación agrupadas en órdenes de magnitud respecto a la totalidad (T) o a ellas mismas:
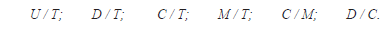
Donde T corresponde al valor para la proporción S/k, es decir la totalidad.
Materiales y métodos
Partiendo de diez Holters, denominados prototipos, tres normales y siete con diferentes enfermedades: dos con enfermedad aguda, cuatro con enfermedad crónica y uno en el límite inferior de normalidad, –diagnosticados por un especialista, de acuerdo con los parámetros clínicos convencionales, los normales examinados voluntariamente para efectos de la investigación– (Tabla 1), y a partir de su frecuencia cardiaca mínima y máxima, y el número de latidos en cada hora, se generó una simulación de los valores consecutivos de la frecuencia cardiaca, con un software diseñado para tal efecto, de la misma forma que se realizó en un trabajo previo (12).
Partiendo de los valores simulados se plantea en esta nueva metodología la construcción de un mapa de retardo (ver definiciones), donde se cuantifica la frecuencia de aparición de cada par ordenado consecutivo de la frecuencia cardiaca en rangos de a cinco, para cada paciente, de tal modo que el atractor construido no es representado mediante trazados irregulares de un punto a otro, como se hace tradicionalmente, sino cuantificando en cada espacio la frecuencia de cada valor consecutivo para los pares ordenados de la frecuencia cardiaca (Figuras 1 y 2). Estos diez prototipos fueron seleccionados por abarcar un rango amplio de edades, desde los 21 años hasta los 81, así como un rango amplio de los valores medios (51-98), mínimos (32-55) y máximos (87-164) de la frecuencia cardiaca y por ser dinámicas particulares excluyentes de importancia clínica como dinámicas normales, tiempo de la onda P a R en el límite inferior de normalidad, crónicos y agudos, lo cual permite desarrollar un proceso inductivo desde estos prototipos particulares en el contexto de un espacio de fases finito universal para todos los atractores, y así desarrollar una generalización con la ley de la probabilidad y la entropía no equiprobable, aplicable a pacientes que se encuentren dentro de estos rangos numéricos.
A partir de los valores de la frecuencia cardiaca mínima y máxima registradas para cada Holter prototipo de normalidad durante la duración total del examen, que fueron 48–116, 41–164 y 37–156 respectivamente, y de los valores mínimos y máximos registrados cada hora, se observa que existen valores de la frecuencia cardiaca comunes para los tres prototipos, y valores que no son comunes a todos. De igual forma, partiendo de los valores de la frecuencia cardiaca mínima y máxima registradas para todos los Holter prototipos de normalidad durante la duración total del examen, que fueron 37–164 y para los prototipos de anormalidad que fueron 32–156, se observa que existen valores de la frecuencia cardiaca que se presentan en los prototipos de anormalidad y no en los prototipos de normalidad, por la tanto se definieron tres regiones dentro del espacio de fases, que representan dichos valores de la frecuencia cardiaca, así:
- Región uno: abarca a todos los rangos de la frecuencia cardiaca que fueron comunes a los Holter normales.
- Región dos: abarca la totalidad de los rangos ocupados por Holter normales, excluyendo los de la región uno.
- Región tres: incluye los rangos de la frecuencia cardiaca que no son ocupados por los prototipos normales, es decir la región restante total del mapa de retardo.
Estas regiones se escogieron para realizar comparaciones entre los atractores de normalidad y anormalidad y evolución entre estos estados.
Luego se definió un espacio de probabilidad donde cada pareja de frecuencias cardiacas se considera como un evento, evaluando para cada región y cada examen la probabilidad de ocupación respecto a la totalidad, cuantificando la probabilidad para cada uno de los rangos de a cinco en el espacio de fases, para luego evaluar la entropía de cada atractor, y posteriormente comparar normalidad y enfermedad crónica y aguda y la posible evolución entre normalidad y enfermedad.
Finalmente se despejó de la fórmula de la entropía (ver definiciones) (ecuación 1), la relación S/k (ecuación 2), la cual es igual a la sumatoria de la probabilidad de ocupación de cada rango de cinco por su logaritmo, para luego agrupar los sumandos que corresponden a probabilidades asociadas a frecuencias de ocupación entre 1-9 (unidades), 10-99 (decenas), 100-999 (centenas) y 1000-9999 (miles), (ecuación 3), desarrollando dichas sumas (ecuación 4), para posteriormente evaluar las proporciones existentes entre cada sumando respecto a la totalidad (proporción S/k) y las proporciones entre centenas respecto a miles y decenas respecto a centenas para cada región determinada.
Análisis físico-matemático de las dinámicas
Diferenciación entre dinámicas normales, agudas y crónicas
En las tres regiones se compararon las proporciones analizadas para todos los prototipos, determinando igualdades y diferencias en las proporciones respecto a normalidad y enfermedad. Para ello se determinaron los valores máximo y mínimo de cada proporción en cada región estudiada para los prototipos de normalidad, y luego se compararon estos rangos con las medidas obtenidas para los prototipos anormales con el objetivo de determinar si sus valores se encuentran dentro de los rangos de normalidad o no. Para cada valor de las proporciones que no se encontró incluido dentro del rango respectivo de normalidad, se realizó una resta siguiendo la siguiente regla: si el valor es menor que el límite inferior de normalidad entonces del límite inferior de normalidad se resta el valor analizado, pero si el valor es mayor que el límite superior de normalidad se resta de dicho valor el límite superior de normalidad, y así se cuantifica específicamente cada dinámica, respecto a la normalidad.
Cuantificación preventiva: especificación de la enfermedad y evolución entre normalidad y enfermedad
Con base en las regiones establecidas, los rangos de normalidad que se determinan al aplicar la metodología y debido a que existen diferentes grados de compromiso en la anormalidad, las restas de las proporciones que no se encontraron dentro del rango de normalidad se ordenaron en cuatro grupos: un grupo para las restas de las proporciones asociadas a frecuencias de aparición de miles, otro para las de centenas, otro para las de decenas, y otro para las de unidades. Finalmente, se sumaron los valores de cada grupo obteniendo un único valor para cada uno de los cuatro órdenes de magnitud evaluados, para así cuantificar qué tan alejada está una dinámica anormal, pues cuanto mayores sean estos valores más alejado estará un paciente de los límites de normalidad. Permite además que al evaluar en el tiempo a un mismo paciente se pueda determinar si está evolucionando hacia la anormalidad o la normalidad comparando si aumentan o disminuyen estos valores respectivamente.
Confirmación de la inducción
Posteriormente se seleccionaron veinte casos particulares, sobre los cuales se aplicó la metodología planteada con el objetivo de confirmar la validez de las predicciones realizadas por medio de una comparación porcentual.
Metodología estadística
Paralelamente se seleccionó una población de cien pacientes y se excluyeron aquellos con edad menor a 21 años; partiendo de los exámenes restantes se realizó un muestreo aleatorio simple (mediante una tabla de aleatorización), seleccionando una muestra de treinta pacientes para los cuales se enmascararon las conclusiones de la lectura del Holter y los antecedentes clínicos registrados en éstos. Debido a que para aplicar la metodología físico-matemática son necesarios los valores mínimos, máximos y total de latidos registrados en el Holter para cada hora, estos resultados no se enmascararon.
Posteriormente se aplicó la metodología físico-matemática planteada en este trabajo a dicha muestra, se desenmascararon los resultados diagnósticos del Holter que se tomaron como estándar de oro, y se calcularon sensibilidad, especificidad y tasa de falsos negativos y de falsos positivos por medio de una tabla de contingencia de 2*2, con respecto a los resultados matemáticos y finalmente se evaluó el nivel de concordancia entre el estándar de oro y el diagnóstico físico matemático mediante el coeficiente Kappa. Además, después de desenmascarar los resultados se observó si existieron exámenes dentro de la muestra que correspondieran a un mismo paciente en diferentes tiempos, con el fin de evaluar su posible evolución.
Resultados
Generales
Se encontró que las parejas ordenadas en rangos de a cinco para las frecuencias cardiacas de los tres Holter normales, variaron entre (50,50) y (170,170), mientras que para los siete enfermos entre (45,45) y (145,145); se encontraron 17 rangos asociados a los pares ordenados de frecuencias cardiacas que aparecen de forma simultánea en los tres trazados de los Holter normales (región uno), y se encontraron 25 rangos totales. Estos son los rangos que incluyen a todos los pares ordenados de la frecuencia cardiaca para los tres holter normales, excluyendo los de la región uno (región dos).
Se encontró que los valores para la frecuencia de ocupación de las parejas de la frecuencia cardiaca en el espacio de fases, variaron entre 0 y 9.522 con valores de probabilidad de 0 y 0,142 respectivamente. Se encontró que los valores de la entropía para los atractores variaron entre 4,40x10-23 y 7,09x10-23, y que valores de las entropías iguales o menores a 5,07x10-23 corresponden a casos agudos (Tabla 2). Se encontró que los valores de entropía para los Holter normales variaron entre 6,39x10-23 y 7,09x10-23, para los Holter con diagnóstio de infarto agudo del miocardio entre 4,40x10-23 y 5,07x10-23 y para los demás Holter prototipos de anormalidad (casos crónicos) entre 5,41x10-23 y 6,96x10-23, de lo que se puede deducir que los rangos de variación para dinámicas normales y agudas están completamente diferenciados y que valores intermedios entre estos rangos se presentan con enfermedad crónica en algunos casos, lo cual se había encontrado previamente al estudiar los espacios de ocupación de atractores clásicos en el espacio de fases con la geometría fractal (12). Los resultados anteriores para la entropía muestran que ésta es una medida que cuantifica la evolución entre normalidad enfermedad, pasando por enfermedades crónicas hasta llegar a agudas, con el decrecimiento respectivo de su valor.
Se encontró que las diferentes proporciones para los sumandos de la entropía de los Holter normales en la región uno variaron entre 0 y 3,607, para la región dos entre 0 y 3,301 para los anormales estos valores en la región uno variaron entre 0 y 1,9029, para la región dos entre 0 y 7,001 y para la región tres entre 0 y 0,8983 (Tabla 3). En las dinámicas crónicas y agudas las restas para las proporciones que no se encontraron dentro de los límites de normalidad variaron entre 0,00006 y 3,69926 y las sumas de dichas restas agrupadas variaron entre 0 y 3,7336 (Tabla 3).
Método de ayuda diagnóstica para diferenciar dinámicas normales, agudas y crónicas
Por lo menos dos de las proporciones evaluadas para los atractores anormales en cualesquiera de las regiones no están contenidas dentro de los límites de normalidad, lo cual permite diferenciar las dinámicas normales de las anormales; así, por ejemplo, los límites de normalidad en la región uno para la proporción D/T, variaron entre 0,0389 y 0,0923, para la proporción C/T entre 0,4825 y 0,5516, para la proporción D/C entre 0,0807 y 0,1904, en la región tres para la proporción U/T entre 0 y 0 y para la proporción D/T entre 0 y 0 y el paciente A1 tuvo un valor de 0,0939, 0,4466, 0,2103, 0,0008 y 0,0104 respectivamente para cada una de estas proporciones; estos valores se encuentran fuera de los límites de normalidad.
Cuantificación preventiva: especificación de la enfermedad y evolución entre normalidad y enfermedad
Se encontró que todas las dinámicas anormales presentaron valores específicos cada una, para la agrupación en órdenes de magnitud de las proporciones que estuvieron fuera de los rangos de normalidad. Solamente tres de los atractores presentaron proporciones que corresponden a miles fuera del rango de normalidad, de los cuales dos presentaron infarto agudo del miocardio (A6 y A7) (Tabla 1), mientras que el tercero (A2), que tuvo mareo, dolor anginoso persistente y un total de 54 ectópicos supraventriculares, presentaron un valor inferior 13 y 42 veces respecto a los pacientes A6 y A7 respectivamente, lo que muestra una diferenciación entre los dos atractores con enfermedad aguda y los pacientes con enfermedad crónica. De esta forma se establece la cuantificación específica para los Holter, evaluando gradualmente las proporciones que se encuentran fuera de los rangos de normalidad así: primero se tendrán en cuenta las proporciones que corresponden a miles, luego las de centenas, decenas y finalmente las de unidades. Así un Holter estará mas alejado de la normalidad si presenta proporciones correspondientes a miles fuera de los límites de normalidad, alejado en menor grado si presenta dichas proporciones solamente en centenas, en menor grado si presenta dichas proporciones solamente en decenas, y finalmente en menor grado que los anteriores si presentan proporciones fuera de normalidad solamente en unidades. De igual forma entre mayor sea la diferencia entre el valor fuera de la normalidad respecto a los límites mas estará alejado el Holter de la normalidad, permitiendo hacer evaluaciones en el tiempo para un mismo paciente del cambio de estos valores y determinar su evolución a normalidad o enfermedad y además cuantificar de forma preventiva la dinámica cardiaca. Esto se evidencia también con el paciente A10 cuyo diagnostico es PR en el límite inferior de normalidad y que solamente presenta una suma asociada con centenas y es la menor de todos los pacientes anormales estudiados.
Confirmación de las predicciones
Los veinte Holter seleccionados presentaron anormalidades clínicas y el número de proporciones fuera de los límites de normalidad osciló entre 5 y 9 por Holter (Tabla 4), lo cual valida las predicciones que aquí se plantean. Todas las dinámicas anormales presentaron valores específicos cada una, para la agrupación en órdenes de magnitud de las proporciones que estuvieron fuera de los rangos de normalidad. Las restas para las proporciones que no se encontraron dentro de los límites de normalidad variaron entre 0,00004 y 2,4608; no se muestran datos. Finalmente las sumas de dichas restas agrupadas variaron entre 0 y 2,83, y solamente tres de estos pacientes presentaron valores mayores a uno en el valor que agrupa las proporciones que corresponden a miles de los cuales dos tienen infarto agudo del miocardio y uno marcapasos, encontrando 100% de acierto con respecto a las predicciones (Tabla 4).
Estudio estadístico
Para los treinta Holters seleccionados el número de proporciones fuera de los límites de normalidad osciló entre 0 y 11 (Tabla 4); para los Holters normales ninguna proporción estuvo fuera de los límites de normalidad, mientras que para los anormales este valor osciló entre 2 y 11, lo cual confirma las predicciones realizadas. Todas las dinámicas anormales presentaron valores específicos cada una, para la agrupación en órdenes de magnitud de las proporciones que estuvieron fuera de los rangos de normalidad y las restas para las proporciones que no se encontraron dentro de los límites de normalidad variaron entre 0,00008 y 26,4412; no se muestran datos. Finalmente las sumas de dichas restas agrupadas variaron entre 0 y 26,56 (Tabla 4). Se encontró además que solamente tres de estos pacientes presentaron valores mayores a uno en el valor que agrupa las proporciones que corresponden a miles de los cuales uno posee marcapasos y los otros dos indican palpitaciones y son los que tienen mayor número de ectopias supraventriculares de la muestra seleccionada: 2.650 y 94 respectivamente (Tabla 4). Luego de desenmascarar los resultados diagnósticos de los Holter para la muestra seleccionada, siendo este el estándar de oro, la medida de sensibilidad fue de 100%, la de especificidad de 100% y la de tasa de falsos positivos y negativos de 0%, respectivamente. De acuerdo con el coeficiente Kappa, el diagnóstico que se obtuvo mediante la metodología desarrollada, fue de 1,00 con respecto al estándar de oro, correspondiente al más alto nivel de concordancia posible.
Cuantificación de la evolución
Al tener un rango de normalidad y todas las posibles proporciones que pueden o no estar fuera de este rango, se pueden hacer comparaciones a priori para el cambio de estos valores en el contexto de la evolución normalidad-anormalidad para un mismo paciente, sin la necesidad de comprobarlo en el tiempo.
Así por ejemplo, después de desenmascarar los resultados convencionales del Holter se encontró que solamente tres correspondieron a un mismo paciente y se realizaron en diferentes tiempos; estos corresponden en orden temporal a los Holter número I33, I34 y E1, (Tabla 4), que son el control realizado a un paciente después de una operación de ablación exitosa, lo cual se comprobó a través de la disminución progresiva del valor que cuantifica las proporciones de miles fuera de los límites de normalidad, siendo estos valores: 0,88, 0,60 y 0,41 respectivamente (Tabla 4). De esta forma, las sumas que cuantifican en órdenes de magnitud a las proporciones que se encuentran fuera de los límites de normalidad evaluadas en el tiempo, permiten cuantificar la evolución hacia los estados de normalidad o anormalidad por el decrecimiento o aumento de las mismas respectivamente, y teniendo en cuenta como se aclaró previamente que las sumas que corresponden a los miles deberán ser tomadas como las más importantes, luego las sumas que corresponden con centenas, luego las de decenas y finalmente las de unidades.
La diferencia entre el atractor representado gráficamente en las figuras 1 y 2, con relación a los tradicionales, es que éstos no poseen una cuantificación de las frecuencias de aparición de cada punto, mientras los que se representan en las figuras 1 y 2 sí, lo que permite hacer una cuantificación matemática a partir de la ley de la probabilidad y la entropía, base fundamental de la metodología predictiva y de ayuda diagnóstica desarrollada en este trabajo.
Discusión
Este es el primer trabajo en el que se desarrolla un nuevo método de ayuda diagnóstica para el Holter a partir de la evaluación de las proporciones de la entropía en la ocupación de pares ordenados dinámicos de los atractores caóticos en el espacio de fases, evidenciando la existencia de un orden subyacente a la impredecibilidad del caos en la dinámica cardiaca mediante el cual se predicen diferencias entre normalidad, anormalidad y evolución entre estos estados, de aplicación clínica a cada caso particular, preventiva e independiente de la patología, intervenciones, y edad si es mayor de 21 años. El establecimiento de los rangos de evolución normalidad-enfermedad puede hacerse de manera más precisa sin que cambie la metodología planteada. La confirmación de las predicciones de la teoría corrobora la inducción físico-matemática a partir de diez casos y su aplicación general a cualquier caso particular; es importante aclarar que las predicciones físico-matemáticas son de carácter universal, por lo que no necesitan una validación estadística; sin embargo dicha validación se realizó para cumplir con los requisitos de la literatura médica actual.
En esta metodología se realiza un experimento donde no se tienen en cuenta las condiciones iniciales; además se estudian las diferentes probabilidades de ocupación de acuerdo con su orden de magnitud (unidades, decenas, centenas y miles), comparándolas en el contexto de la entropía no equiprobable, encontrando estados geométricos intrínsecos que predicen las diferencias entre normalidad y anormalidad, y evidenciando una auto-organización del atractor, es decir, un orden predecible desde las proporciones de una ley de la naturaleza. Usualmente, la entropía se interpreta como el grado de desorden de un sistema. En este trabajo es una medida de orden que cuantifica las proporciones de ocupación geométrica del atractor, evidenciando que para caracterizar la dinámica cardiaca es necesario establecer relaciones de partes y totalidad de probabilidad y entropía en atractores geométricos y no medidas de la variabilidad, puesto que existen rangos en los que los valores de probabilidad y entropía se superponen; sin embargo la entropía permite diferenciar un grupo de normalidad y crónico de otro de enfermedad aguda.
La simplificación realizada al construir la totalidad de la dinámica a través de los rangos hallados de forma empírica en el Holter, muestra que desde planteamientos teóricos es posible crear las rutas que toma un atractor para cambiar su estado, permitiendo predecir las posibles formas en las que evoluciona un paciente de normalidad a enfermedad y viceversa, dentro de un espacio acotado y con valores finitos. La cuantificación de los valores predictivos que caracterizan los estados de normalidad y enfermedad, evidencian que esta metodología es de carácter más simple, y que a pesar de que el valor del coeficiente Kappa muestra que la metodología convencional y ésta se corresponden, la metodología física es más específica y eficaz para la evaluación de la dinámica cardiaca con respecto al estándar de oro, presentado por ejemplo con los resultados para los Holter I33, I34, E1 que corresponden a un mismo paciente durante tres días consecutivos después de una operación de ablación, mostrando su evolución hacia la normalidad por la reducción en los valores de las sumas de las restas de las proporciones que no se encontraron dentro de los límites de normalidad y que corresponden a miles (Tabla 4). Esto evidencia las implicaciones a nivel clínico, farmacológico y diagnóstico de esta metodología, pues permite prevenir la evolución de dinámicas normales a enfermas y evaluar las intervenciones farmacológicas y las indicaciones quirúrgicas y médicas, o ambas.
Las metodologías de diagnóstico clínico de la dinámica cardiaca se basan en clasificaciones (30, 31) de forma similar a las clasificaciones de los cuerpos en la física aristotélica (cuerpos más densos y sutiles); en contraposición, en la teoría de gravitación newtoniana (32, 33) existe una ecuación sobre la totalidad de las dinámicas de los cuerpos densos del universo y no una clasificación. De igual forma, en este trabajo, así como en la mecánica clásica, se plantea una metodología universal que contiene cualquier posible dinámica cardiaca y su cuantificación dentro de la normalidad o su separación de ésta, así como la evaluación de cualquier estado de evolución de estos valores con fines clínicos. Por ejemplo, dos pacientes (A6 y A7), con la misma clasificación clínica (infarto agudo del miocardio), presentan valores diferentes en las restas de las proporciones que están fuera del rango de normalidad; en el caso de las agrupadas en miles la del paciente A7 es 3,2 veces mayor que la del A6, lo que muestra que una misma clasificación se cuantifica de forma diferente y más específica por la metodología que aquí se plantea.
Carnot enunció por primera vez el concepto de entropía en la termodinámica; esta teoría busca establecer leyes entre las diversas propiedades de la materia sin tener en cuenta su estructura interna (15), y la definió como una igualdad entre las proporciones del calor dado a una máquina junto con el valor de la temperatura del contenedor que cede dicha temperatura, y el calor cedido por la máquina a otro contenedor con otra temperatura. Posteriormente, en la teoría cinética de los gases, Boltzmann definió la entropía como una medida proporcional al logaritmo del número de microestados equivalentes a nivel macroscópico. Luego la entropía fue redefinida y generalizada en la mecánica estadística, para los sistemas fuera del equilibrio constituyéndose como una medida proporcional a la suma de los productos de la probabilidad de cada microestado por su logaritmo, siendo la constante de proporcionalidad la constante de Boltzmann (16, 17). De igual modo, la entropía ha sido generalizada en el contexto de su conservación en la forma de información holográfica donde no hay valores infinitos para ésta (34), y utilizada por Shannon como una medida que cuantifica la cantidad de información que posee un sistema de forma objetiva (18). En este trabajo la entropía no equiprobable se estructura en relaciones geométricas de la dinámica estudiada en donde las distribuciones de probabilidades se auto-organizan dando cuenta del orden del atractor geométrico.
En una revisión de varios métodos que han sido usados para estimar la complejidad de series de tiempo en el análisis de la dinámica cardiaca realizada por Juha y colaboradores (35), donde se estudiaron los exponentes de Lyapunov (36), la dimensión Haussdorff (36, 37), la dimensión de correlación D2 (36, 38) y la entropía de Kolmogorov (39), se aclara que la aplicabilidad clínica de estos métodos no ha sido bien establecida. La diferencia observada en un trabajo previo entre pacientes con enfermedad aguda y pacientes con enfermedad crónica y normales para el Holter en adultos (12), se halló de forma más simple en este trabajo a partir de los valores de la entropía de cada atractor. La especificidad para la diferenciación y predicción a partir de las proporciones de la entropía vistas en este trabajo, evidencia la dificultad de encontrar una aplicación clínica a partir de la evaluación matemática de la variabilidad de la frecuencia cardiaca, pues las proporciones de la entropía Boltzmann-Gibbs son sensibles a las distribuciones no equiprobables de los espacios de probabilidad y sus cambios, así como a su evaluación de acuerdo con las frecuencias de aparición, permitiendo un análisis del orden matemático de la totalidad del fenómeno, mientras que el análisis aislado de la variabilidad de la frecuencia no permite evidenciar este orden subyacente. La cuantificación de la entropía aproximada a la frecuencia cardiaca corresponde a trabajos particulares aplicados a problemas específicos (24-29), mientras que este trabajo es una universalización a partir de una inducción para cualquier caso particular.
El orden físico y matemático evidenciado no se correlaciona con la aleatoriedad ni el azar de los sistemas dinámicos (40) pues se evidenció que las proporciones probabilísticas en el contexto de la entropía permiten realizar diferenciaciones clínicas de las dinámicas cardiacas, de forma similar con una proteína teórica construida con un generador pseudo-aleatorio y péptidos que se unen o no en un trabajo de predicción de péptidos de unión al HLA clase II, donde se evidenciaron órdenes subyacentes fundamentales (41). Dos concepciones han sido fundamentales en la física teórica: Einstein quien dice que «Dios no juega a los dados» lo que implica que los fenómenos pueden ser deterministas, como por ejemplo sus resultados de la relatividad especial y general, en contra de la posición de Bohr, quién dice que «Dios sí juega a los dados» como en la mecánica cuántica, permitiendo sistemas indeterminados y aleatorios (42). El resultado determinista de este trabajo se logra al considerar una posición determinista-indeterminista simultánea, en la cual se consideró que «Dios juega a los dados, pero cargados», así el determinismo y el indeterminismo conviven y esta concepción se introdujo en la fórmula de la entropía Boltzmann-Gibbs para ver los cargamientos de las distribuciones de las probabilidades y poder determinar las proporciones de esas distribuciones de probabilidades; así los atractores caóticos se convierten en atractores geométricos con órdenes matemáticos predecibles a partir de esta reinterpretación de la entropía.
En trabajos anteriores se había propuesto una nueva visión en la medicina (5, 12, 41, 43-48) basada en el desarrollo de teorías predictivas, que así como la teoría de gravitación universal puede predecir de manera objetiva y absolutamente determinista un eclipse, logrará encontrar resultados del mismo nivel en el desarrollo de diagnósticos médicos; en este trabajo se desarrolló una teoría que predice de manera objetiva y determinista desde la teoría de la probabilidad, el principio de la entropía proporcional y la geometría de los sistemas dinámicos las dinámicas cardiacas en el contexto de un método de ayuda diagnóstica. Así como en la física no es necesario desarrollar un tratamiento estadístico para predecir un eclipse, de igual forma las predicciones de esta teoría son independientes de la validación estadística.
La capacidad de caracterización y predicción de una dinámica aparentemente caótica como la cardiaca por medio de esta metodología, sugiere que el orden subyacente encontrado puede constituir un principio general para cualquier sistema dinámico caótico.
Dedicatoria
Al Maestro Isaac Newton por su devoción al misterio.
Al Maestro Maharishi Mahesh Yogi por enseñar la meditación que da la paz al corazón de la creación.
A mis hijos.
A la L, a Diego Armando Maradona, al Boca Juniors y a la Selección de Argentina por hacerme creer que la entrega total es la que lleva a los resultados.
Agradecimientos
Al Grupo Insight por creer y crear la mística y la entrega de mi corazón.
A la clínica del Country, en especial a la doctora Natalia Malaver, directora del Centro de Investigaciones, y al doctor John Ayala, cardiólogo de la institución, por apoyar mis investigaciones.
A Cardiolog, por facilitarnos la toma de los Holter de los casos normales, y a su enfermera Miriam Parada, por su colaboración en la toma de los mismos.
Al Doctor Guillermo Mora, profesor de Medicina de la Universidad Nacional, por facilitarnos conocimientos sobre la aplicación y análisis del Holter, así como Holter usados en este estudio.
A la Doctora Luisa Fernanda Benítez, por sus sugerencias epidemiológicas.
Bibliografía
1. Devaney R. A first course in chaotic dynamical systems theory and experiments. Reading Mass.: Addison- Wesley; 1992. p. 1-48. [ Links ]
2. Peitgen, H. Length area and dimension. Measuring complexity and scalling properties. En: Chaos and Fractals: New Frontiers of Science. Springer-Verlag. N.Y. 1992. p. 183-228. [ Links ]
3. Mandelbrot B. The fractal geometry of nature. Freeman. Tusquets Eds. S.A. Barcelona; 2000. p. 341-8. [ Links ]
4. Peitgen H, Jurgens H, Saupe D. Chaos and fractals: new frontiers of science. Springer-Verlag. N.Y.; 1992. p. 67-766. [ Links ]
5. Rodríguez J. Comportamiento fractal del repertorio T específico contra el alergeno Poa P9. Rev Fac Med Univ Nac Colomb 2005; 53 (2): 72-8. [ Links ]
6. Goldberger A, West BJ. Fractals in physiology and medicine. Yale J Biol 1987; 60: 421-35. [ Links ]
7. Goldberger A, Rigney D, West B. Chaos and fractals in human physiology. Sci Am 1990; 262: 42-49. [ Links ]
8. West, B. J. Fractal physiology and chaos medicine. London: World Scientific Publishing, Co.; 1990. [ Links ]
9. Goldberger A, Amaral L, Hausdorff J, Ivanov P, Peng C, Stanley H. Fractal dynamics in physiology: alterations with disease and aging. Proc Natl Acad Sci USA 2002; 99 (suppl 1): 2466-72. [ Links ]
10. Gough N. Fractals, chaos, and fetal heart rate. Lancet 1992; 339: 182-3. [ Links ]
11. Denton T, Diamond G, et al. Fascinating rhythm: a primer on chaos theory and its application to cardiology. Am Heart J 1990; 6 (1): 1419-40. [ Links ]
12. Rodríguez J, Prieto S, Avilán N, Correa C, Bernal P, Ortiz L, Ayala J. Nueva metodología física y matemática de evaluación del Holter. Rev Colomb Cardiol 2008; 15: 50-4. [ Links ]
13. Palma J, Arribas A, Ramón J, Juanatey G, Marín E, Simarro E, Guías de práctica clínica de la Sociedad Española de Cardiología en la monitorización ambulatoria del electrocardiograma y la presión arterial. Rev Esp Cardiol 2000; 53: 91-109. [ Links ]
14. Feynman RP, Leighton RB, Sands M. Probabilidad. En: Física. Feynman RP, Leighton RB, Sands M. Física. Vol. 1. Primera edición Wilmington: Addison-Wesley Iberoamericana, S. A. México; 1998. p. 6-1, 6-16. [ Links ]
15. Feynman RP, Leighton RB, Sands M. Leyes de la termodinámica. En: Física. Feynman RP, Leighton RB, Sands M. Física. Vol. 1. Primera edición Wilmington: Addison-Wesley Iberoamericana, S. A. México; 1998. p. 44-1, 44-19. [ Links ]
16. Matvéev A. Física molecular. Primera edición, Moscú; 1987 MIR. [ Links ]
17. Tolman R. Principles of statistical mechanics. Primera edición. New York: Dover Publications; 1979. [ Links ]
18. Frodden E, Royo J, Entropía e información, Seminario Final del curso de Termodinámica, Depto. de Física, Facultad de Ciencias, Universidad de Chile, 2004. Disponible en http://fisica.ciencias.uchile.cl/~gonzalo/cursos/termo_II-04/ seminarios/seminarios1.htm [ Links ]
19. Pincus SM, Gladstone IM, Ehrenkranz RA. A regularity statistic for medical data analysis. J Clin Monit 1991; 7 (4): 335-45. [ Links ]
20. Bein B. Entropy. Best Practice & Research Clinical Anaesthesiology 2006; 20 (1): 101-9. [ Links ]
21. Pincus SM, Goldberger AL. Physiologic time-series analysis: what does regularity quantify? Am J Physiol 1994; 226: H1643-56. [ Links ]
22. Pincus SM, Viscarello RR. Approximate entropy: a regularity statistic for fetal heart rate analysis. Obstet Gynecol 1992; 79: 249-55. [ Links ]
23. Pincus SM, Huang WM. Approximate entropy: statistical properties and applications. Commun Stat Theory Meth 1992; 21: 3061-77. [ Links ]
24. Perkio J, Zareba W, Badilini F, Moss AJ. Influence of atropine on fractal and complexity measures of heart rate variability. Ann Noninv Electrocardiol 2002; 7: 326-31. [ Links ]
25. Tulppo MP, Ma¨kikallio TH, Takala TE, Seppa¨nen T, Huikuri HV. Quantitative beat-to-beat analysis of heart rate dynamics during exercise. Am J Physiol 1996; 271: H244-52. [ Links ]
26. Lin LY, Lin JL, Du CC, Lai LP, Tseng YZ, Huang SKS. Reversal of deteriorated fractal behavior of heart rate variability by beta-blocker therapy in patients with advanced congestive heart failure. J Cardiovasc Electrophysiol 2001; 12: 26-32. [ Links ]
27. Vikman S, Mäkikallio TH, Yli-Mäyry S, Pikkujämä S, Koivisto AM, Reinikainen P, Airaksinen KE, Huikuri HV. Altered complexity and correlation properties of RR interval dynamics before the spontaneous onset of paroxysmal atrial fibrillation. Circulation 1999; 100: 2079-84. [ Links ]
28. Hogue CW Jr., Domitrovich PP, Stein PK, Despotis GD, Re L, Schuessler RB, et al. RR interval dynamics before atrial fibrillation in patients after coronary artery bypass graft surgery. Circulation 1998; 98: 429-34. [ Links ]
29. Fleisher LA, Pincus SM, Rosenbaum SH. Approximate entropy of heart rate as a correlate of postoperative ventricular dysfunction. Anesthesiology 1993; 78: 683-92. [ Links ]
30. JMO Arnold, P Liu, C Demers, et al. Canadian Cardiovascular Society consensus conference recommendations on heart failure 2006: Diagnosis and management. Can J Cardiol 2006; 22 (1): 23-45. [ Links ]
31. Comisión de Evaluación Diagnóstica de la Insuficiencia Cardíaca. Consenso De Insuficiencia Cardiaca. Rev Arg Cardiol 2000; 68 (3): 10-28. [ Links ]
32. Feynman RP, Leighton RB, Sands M. La teoría de la gravitación. En: Física. Feynman RP, Leighton RB, Sands M. Física. Vol. 1. Primera edición México; Wilmington: Addison-Wesley Iberoamericana, S. A. 1998. p. 7-1, 7-17. [ Links ]
33. Feynman RP, Leighton RB, Sands M. Leyes de Newton de la dinámica. En: Física. Feynman RP, Leighton RB, Sands M. Física. Vol. 1. Primera edición, México, Wilmington: Addison-Wesley Iberoamericana, S. A. 1998. p. 9-1, 9-14. [ Links ]
34. Bekenstein J. La información en el Universo holográfico. Investigación y ciencia; 2003. p. 36-43. [ Links ]
35. Juha S. PerkiöMä Ki, Timo H. Mä Kikallio, Heikki Huikuri. Fractal and complexity measures of heart rate variability. Clin Exp Hypertens 2005; 2 y 3: 149-58. [ Links ]
36. Eckmann JP, Ruelle D. Ergodic theory of chaos and strange attractors. Rew Mod Physics 1985; 7: 617-56. [ Links ]
37. Babyloyantz A, Destexhe A. Is the normal heart a periodic oscillator? Biol Cybern 1988; 58: 203-11. [ Links ]
38. Grassberger P, Procaccia I. Measuring the strangeness of strange attractors. Physica 1983; 9D: 189-208. [ Links ]
39. Grassberger P, Procaccia I. Estimation of the Kolmogorov entropy from a chaotic signal. Phys Rew A 1983; 28: 2591-3. [ Links ]
40. Chaitin GJ. Aritmética y azar. Investigación y Ciencia 1988; 144: 44-50. [ Links ]
41. Rodríguez J. Teoría de unión al HLA clase II teorías de probabilidad combinatoria y entropía aplicadas a secuencias peptídicas. Inmunología 2008; 27 (4): 151-66. [ Links ]
42. Calude CS, Stay MA. From Heisenberg to Godel via Chaitin. Int J Theoretical Physics 2007; 46 (8): 2013-25. [ Links ]
43. Rodríguez J, Mariño M, Avilán N, Echeverri D. Medidas fractales de arterias coronarias, un modelo experimental en re-estenosis, armonía matemática intrínseca de la estructura arterial. Rev Col Cardiología 2002; 10: 65-72. [ Links ]
44. Rodríguez J, Prieto S, Ortiz L, et al. Diagnóstico Matemático de la monitoria fetal aplicando la ley de Zipf-Mandelbrot. Rev Fac Med Univ Nac Colomb 2006; 54 (2): 96-107. [ Links ]
45. Rodríguez J. Dynamical systems theory and ZIPF – Mandelbrot Law applied to the development of a fetal monitoring diagnostic methodology. XVIII FIGO World Congress of Gynecology and Obstetric. Kuala Lumpur, MALAYSIA. November 2006. [ Links ]
46. Rodríguez J, Prieto S, Ortiz L, Wiesner C, Díaz M, Correa C. Descripción matemática con dimensiones fractales de células normales y con anormalidades citológicas de cuello uterino. Rev Cienc Salud 2006; 4 (2): 58-63. [ Links ]
47. Rodríguez J. Diferenciación matemática de péptidos de alta unión de MSP-1. 2 mediante la aplicación de la teoría de conjuntos. Inmunología 2008; 27 (2): 63-8. [ Links ]
48. Rodríguez J. Caracterización física y matemática de péptidos de alta unión de MSP-1 mediante la aplicación de la teoría de la probabilidad y la entropía. Arch Alerg Inmunol Clín 2008; 39 (2): 74-82. [ Links ]














