Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Colombiana de Cardiología
Print version ISSN 0120-5633
Rev. Colomb. Cardiol. vol.19 no.1 Bogota Jan./Feb. 2012
Diagnóstico fractal del ventriculograma cardiaco izquierdo
Geometría fractal del ventriculograma durante la dinámica cardiaca
Fractal geometry of ventriculogram during cardiac dynamics
Javier Rodríguez; MD.(1, 2), Signed Prieto(1, 2), Catalina Correa, PSY(1, 2); Pedro Bernal(1, 2), Luisa Álvarez, PSY. (1, 3); Germán Forero, MD.(2); Sarith Vitery(2); Germán Puerta(2); Ingrid Rojas(2)
(1) Grupo Insight. Bogotá, DC., Colombia.
(2) Línea de Profundización e Internado Especial en Teorías Físicas y Matemáticas aplicadas a la Medicina: Universidad Militar Nueva Granada – Clínica del Country. Bogotá, DC., Colombia.
Correspondencia: Dr. Javier Rodríguez Velásquez. Cra. 79B N° 51-16 Sur. Int. 5. Apto. 102, Barrio Kennedy, Bogotá D.C., Colombia. Teléfono: 4 52 75 41. Correo electrónico: grupoinsight2025@yahoo.es
Recibido: 15/06/2011. Aceptado: 23/09/2011.
Antecedentes y objetivos: la geometría fractal permite describir y caracterizar los objetos irregulares, lo que resulta adecuado para medir estructuras del cuerpo humano. El propósito de este trabajo es caracterizar el ventrículo izquierdo durante la dinámica cardiaca con dimensiones fractales para desarrollar un diagnóstico matemático objetivo y reproducible de la ventriculografía izquierda.
Método: este es un estudio de concordancia diagnóstica donde se calcularon las dimensiones fractales del ventrículo en sístole, en diástole y en un total de 36 ventriculogramas evaluados como normales, y anormales en leves, moderados y severos de acuerdo con la fracción de eyección según el diagnóstico clínico convencional; posteriormente se determinaron los grados de similitud de las dimensiones fractales entre los tres objetos componentes.
Resultados: los grados de similitud estuvieron entre 1 y 9.000, y al organizar estos valores en conjuntos, se encontró una progresión a partir de los normales hasta los anormales severos. Se establecieron los grados de similitud característicos que permiten diferenciar normalidad de enfermedad y evolución entre éstas, evidenciando que la clasificación de la clínica convencional presenta dificultades al evaluar de forma precisa y objetiva la evolución de un ventriculograma hacia la normalidad o la enfermedad.
Conclusiones: se desarrolló una nueva metodología diagnóstica objetiva y reproducible de aplicación clínica basada en evaluaciones geométricas independiente de la clasificación clínica.
Palabras clave: fractal, diagnóstico, ventrículo izquierdo, ventriculografía izquierda.
Background and Objectives: fractal geometry allows to describe and characterize irregular objects, which is appropriate for measuring human body structures. The purpose of this study is to characterize the left ventricle during cardiac dynamics by means of fractal dimensions to develop an objective, mathematical and reproducible diagnosis of left ventriculography.
Method: this is a diagnostic concordance study in which we calculated the fractal dimensions of the ventricle in systole, in diastole and in a total of 36 ventriculograms evaluated as normal, mild, moderate and severe according to the ejection fraction in accordance with the conventional clinical diagnosis ; subsequently, the degree of similarity of the fractal dimensions between the three components were determined.
Results: the degrees of similarity were between 1 and 9,000, and when arranging these values into sets, there was a progression from normal to severe. We established the characteristic degrees of similarity that allow to distinguish normality from disease and the evolution between them, showing that the conventional clinical classification presents difficulties to assess accurately and objectively the evolution of a ventriculogram towards normality or disease.
Conclusions: we developed a new objective and reproducible diagnostic methodology of clinical application based on geometric assessments that is independent from the clinical classification.
Keywords: fractal, diagnosis, left ventricle, left ventriculography.
Introducción
En 1975 Mandelbrot desarrolló la geometría fractal y con el propósito de describir de manera adecuada los objetos irregulares de la naturaleza, definió el concepto de dimensión fractal (1). Existen tres clases de fractales: los matemáticos abstractos, los estadísticos y los salvajes, cada uno de los cuales tiene diferente definición, aplicación y metodología para su obtención (2). Los fractales salvajes son objetos irregulares que se caracterizan por la superposición de sus partes y cuya dimensión fractal se calcula por medio del método de Box-Counting (3).
Se han realizado múltiples aplicaciones de la geometría fractal a la caracterización de la morfología y la dinámica de diferentes tejidos y sistemas. Tal es el caso de la caracterización de los cambios de la irregularidad de células, paredes parenquimales, tejidos y redes vasculares durante el desarrollo neoplásico. Polhman y colaboradores (4) y Lefebvre y Benali (5), por ejemplo, determinaron la utilidad de métodos de análisis fractal en la reducción de diagnósticos falsos positivos en el análisis de mamografías digitales. Los grados de lesión hasta carcinoma en el tejido conectivo epitelial de interfase de la mucosa oral fueron estudiados por Landini y Rippin (6), quienes determinaron un espectro de valores fractales asociado a dichos cambios. Del mismo modo, Gazit y colaboradores (7) establecieron valores fractales característicos de normalidad y enfermedad de la arquitectura y la fisiología tumoral en tumores andrógeno-dependientes de ratones.
Sin embargo, se ha encontrado que no siempre es posible establecer rangos de valores característicos de normalidad y enfermedad, evidenciando que la evaluación de dimensiones fractales aisladas no siempre provee información diagnóstica (8). En este sentido, se han desarrollado trabajos en diferentes áreas de la medicina, en los que se observa la necesidad y utilidad del desarrollo de metodologías y conceptos para el análisis ulterior de las dimensiones fractales. Por ejemplo, se desarrollaron los conceptos de variabilidad y diferencia neta de las dimensiones fractales para el reconocimiento matemático de distintos niveles de gravedad de enfermedad arterial oclusiva evaluada en angiografías (9, 10). También se desarrolló una generalización fractal que permite determinar el total de arterias coronarias normales y restenosadas con base en el concepto de armonía matemática intrínseca (11). Del mismo modo, se desarrolló un diagnóstico clínico de la dinámica cardiaca fetal evaluada en monitorías, con base en la distribución fractal de componentes dinámicos del sistema, evaluados con la dimensión fractal de Zipf Mandelbrot (12), y un método matemático de aplicabilidad clínica para el diagnóstico de células preneoplásicas y neoplásicas del epitelio escamoso cervical, el cual supera el diagnóstico de ASCUS (13).
El ventriculograma, que permite la visualización de la silueta ventricular al final de la sístole y la diástole, se usa para calcular la fracción de eyección (FE) y establecer anomalías en la motilidad de la pared del ventrículo (14), pero su interpretación depende de la experiencia del evaluador. Rodríguez y colaboradores (15) desarrollaron una medida cuantitativa de ventriculogramas normales y con fracción de eyección menor a 40%, con diagnóstico de compromiso ventricular severo, basada en la evaluación de los grados de similitud entre las dimensiones fractales de los contornos ventriculares izquierdos durante la dinámica cardiaca, en sístole, diástole y totalidad, permitiendo establecer una medida objetiva y reproducible, independiente de la experiencia del observador y de ayuda diagnóstica para el ventriculograma.
En la presente investigación se calcularán dimensiones fractales de ventriculogramas normales, leves, moderados y severos, desarrollando un diagnóstico físico y matemático, objetivo y reproducible, de aplicación clínica.
MétodosDefiniciones
Fractal: objeto irregular o irregularidad del mismo.
Dimensión fractal: medida numérica que evalúa la irregularidad de un objeto. En esta investigación se utilizó la definición de dimensión fractal de Box-Counting.
Dimensión fractal de Box-Counting (2):
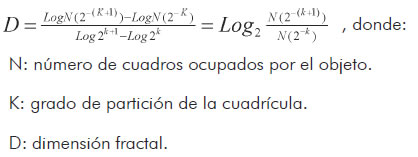
Regiones medidas fractalmente
Sístole (S): región correspondiente a la imagen del ventrículo en sístole.
Diástole (D): región correspondiente a la imagen del ventrículo en diástole.
Totalidad (T): suma de los valores medidos en sístole y en diástole.
Análisis matemático
Grados de similitud: para el cálculo de los grados de similitud se definió un valor para cada cifra de la dimensión fractal. A las unidades se les asignó un valor de 1, a las décimas 10, a las centésimas 100 y a las milésimas 1.000. Comparando las cifras de izquierda a derecha, se ubica la primera cifra que es diferente entre las dimensiones fractales, y se restan sus valores; el resultado de la resta se multiplica por el valor asignado a la cifra1.
Valores generales de posibles grados de similitud ordenados en conjuntos:
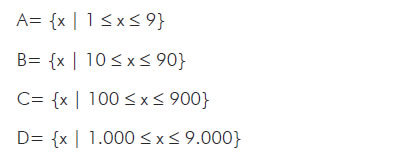
Este es un estudio de concordancia diagnóstica, basado en una metodología de generalización geométrica aplicada a la clínica, en el que se seleccionaron 36 pacientes sin diferenciación de género, sometidos a examen de ventriculografía izquierda por indicación médica, los cuales fueron divididos en cuatro grupos: un grupo de nueve pacientes con fracción de eyección normal, otro de nueve pacientes diagnosticados clínicamente como leves, nueve moderados y nueve severos con fracción de eyección menor a 40%, los cuales fueron escogidos con el fin de tener el espectro completo de relaciones geométricas posibles evaluadas en la clínica para hacer comparaciones con la metodología matemática propuesta. Dicho examen fue realizado y evaluado por especialistas del departamento de Hemodinamia de la Fundación Cardioinfantil - Instituto de Cardiología y las imágenes se obtuvieron a través del sistema ACOM–TOP de SIEMMENS.
Se utilizó la canalización vía percutánea de la arteria femoral para el cateterismo cardiaco, y posteriormente se insertaron catéteres de 5 (de 1,5 mm de diámetro) o 6 french (de 1,8 mm). Se inyectaron, a presión, en la cavidad ventricular izquierda, 30 a 45 mL de medio de contraste a una velocidad de 10 a 12 mL/s. Se seleccionaron tres objetos matemáticos para su caracterización, correspondientes a las imágenes del ventrículo izquierdo en sístole, diástole y la totalidad, a las cuales se les calculó su dimensión fractal con una modificación del método Box-Counting de acuerdo con la metodología utilizada en trabajos anteriores (8-11). Ésta consiste en la simplificación de su cálculo a través del conteo de cuadros mediante la superposición de rejillas de 1 y 2 cm, evaluando los contornos geométricos durante el comportamiento dinámico del sistema, permitiendo así la realización posterior de las respectivas comparaciones entre los objetos evaluados y desarrollándose una metodología evaluativa de la dimensión fractal de objetos definidos independientemente del grado de compromiso.
Con esta metodología se obtienen caracterizaciones matemáticas para cada ventrículo particular y para cada grupo estudiado, lo que posibilita prescindir de metodologías estadísticas y hace innecesario el uso de grandes muestras para comprobar los resultados.
Las dimensiones fractales fueron analizadas comparando cada una de las regiones con las otras dos en busca de las posibles diferencias y/o igualdades entre los grupos del estudio y para cada caso particular, a partir del cálculo del grado de similitud. Finalmente estos valores son comparados intra e intergrupos determinando las características diferenciales de normalidad o enfermedad.
Este trabajo está clasificado en la categoría de investigación sin riesgo, pues se hacen cálculos matemáticos sobre resultados de exámenes de la práctica clínica que han sido prescritos médicamente; así mismo, los resultados de este trabajo no afectan a los pacientes y cumplen con las normas científicas, técnicas y administrativas para la investigación en salud, basadas en la resolución No. 008430 de 1993, específicamente con el título 11 referente a la investigación en seres humanos, respetando su integridad y anonimato.
ResultadosLas dimensiones fractales medidas en sístole oscilaron entre 0,6214 y 1,2064, en diástole entre 0,4361 y 1,4995, y para la totalidad entre 0,5849 y 1,1375. Las dimensiones fractales de ventrículos clasificados clínicamente como normales oscilaron entre 0,4361 y 1,4995, los leves entre 0,6520 y 1,1293, los moderados entre 0,8580 y 1,1375, y los severos entre 0,8813 y 1,1844 (Tabla 1). Los valores de los grados de similitud entre las regiones medidas para los ventriculogramas evaluados con fracción de eyección normal estuvieron en los conjuntos A y B, presentando, generalmente, valores del conjunto A en una de sus comparaciones; en los leves se presentaron los conjuntos A, B y C, igual que en los moderados, y en los severos se encontraron los conjuntos A, B, C y D (Tabla 2).
Los valores para los grados de similitud evidencian una diferenciación matemática entre los ventriculogramas evaluados clínicamente como normales y los evaluados como severos; las tres comparaciones para los normales fueron siempre menores que 90, mientras que en por lo menos una de las comparaciones para los severos se encuentra un valor entre 100 y 9.000 (Tabla 3). Adicionalmente, los grados de similitud representados por los conjuntos C y D, son característicos de por lo menos una de las comparaciones en ventriculogramas severos, mientras que los representados por los conjuntos A y B pueden presentarse en cualquier grupo, pero son característicos del conjunto de casos normales, los cuales sólo pueden tomar estos valores (Figura 1) (Tabla 3).
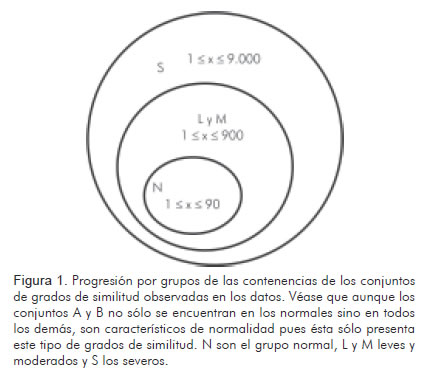

Tres de los ventriculogramas evaluados como leves presentaron en todas sus comparaciones grados de similitud asociados a los de normalidad; así mismo se presentó un caso en los ventriculogramas moderados, evidenciando que los valores asociados a normalidad pueden aparecer en los ventriculogramas evaluados como leves y moderados pero no en los severos. Del mismo modo, los grados de similitud asociados a lesión severa se presentan en todos los casos restantes de los grupos de leves y moderados.
De esta forma, los grupos leves y moderados no presentan características matemáticas diferenciales, lo que sugiere que estas clasificaciones cualitativas son estados de evolución entre la normalidad y la enfermedad. También evidencia la capacidad diagnóstica de la metodología propuesta, pues puede cuantificar qué tan leve o moderada es una disfunción ventricular; es decir, qué tanto dista el compromiso ventricular de la normalidad o del compromiso severo.
Cabe resaltar que sólo se encuentran valores mayores a 1.000 en el grupo de ventriculogramas severos, lo que concuerda con la afirmación de que el aumento de este valor se asocia con disfunciones severas.
La evaluación permite obtener todos los grados de similitud posibles para caracterizar cualquier ventriculograma y evaluar su grado de compromiso, partiendo de todas las combinaciones de grados de similitud viables entre los objetos matemáticos medidos.
DiscusiónEste es el primer trabajo donde se desarrolla un nuevo diagnóstico matemático de la ventriculografía izquierda basado en la geometría fractal y en la definición de grados de similitud. Se calcularon dimensiones fractales de ventriculogramas en sístole, en diástole y en la totalidad, de pacientes normales, leves, moderados y severos de acuerdo con el diagnóstico clínico convencional, evaluándose grados de similitud de las dimensiones fractales entre los objetos definidos y desarrollando una cuantificación geométrica diagnóstica, con implicaciones para cualquier patología cardiaca que tenga repercusiones en la geometría ventricular.
Tanto la función como la morfología cardiaca se evaluaron y relacionaron de forma unificada. Se realizó una abstracción matemática de la totalidad a partir de la suma de los valores de cuadros ocupados en sístole y diástole, permitiendo generalizar las medidas de la estructura ventricular obtenidas durante la dinámica cardiaca. La presente investigación evidencia órdenes de normalidad y enfermedad en la estructura y dinámica del ventrículo izquierdo. El orden develado podría expandir los alcances de las posibilidades metodológicas de investigación científica desarrolladas a partir de simulaciones computacionales, como el caso de las investigaciones de Kappenberger (16) quien mostró cómo la geometría y la anatomía influyen en la estabilidad eléctrica del corazón.
Medidas poblacionales de número mayor de ventriculogramas, no afectarían la metodología propuesta, pues los que tienen fracción de eyección normal están completamente diferenciados de los severos, y en los clasificados como leves y moderados podrían encontrarse tanto ventriculogramas con fracción de eyección normal como severos y progresiones entre estos dos estados, evidenciando la evolución entre normalidad y enfermedad, que ahora serían cuantificados de forma objetiva y reproducible, mediante relaciones matemáticas. Otros trabajos en cardiología implementan medidas físicas o matemáticas junto con análisis estadísticos como el de Huikuri y colaboradores (17), quienes realizaron una caracterización de la dinámica cardiaca aplicando geometría fractal en pacientes con infarto agudo de miocardio con una fracción de eyección menor al 35%, superando los factores predictores de muerte convencionales. Estas investigaciones son útiles para muestras poblacionales. A diferencia del trabajo de Huikuri, el trabajo que aquí se presenta es una generalización geométrica, en la que los resultados son útiles para cualquier muestra poblacional y para cada caso particular.
Múltiples trabajos recientes revelan la importancia y aplicabilidad práctica de teorías físicas y matemáticas para la investigación de los diferentes campos de la medicina. Tal es el caso de caracterizaciones y predicciones en Inmunología y Biología molecular, entre las que se encuentra una predicción del estado de unión o no unión del 100% de los péptidos evaluados, evidenciando un orden matemático acausal subyacente al fenómeno de unión, con base en las teorías de probabilidad, combinatoria y entropía (18) y una teoría predictiva de unión de péptidos de malaria implicados en el proceso de invasión al glóbulo rojo con una especificidad del 90% y una sensibilidad del 95% (19). Se han desarrollado predicciones útiles en la toma de decisiones en salud pública (20), tales como la predicción de brotes de malaria en tres semanas en 820 municipios de Colombia con una eficacia del 99,86% (21). En Cardiología, se han desarrollado trabajos desde la teoría del caos que han permitido establecer una nueva concepción de normalidad–enfermedad que contradice el concepto homeostático tradicional (22), y se han desarrollado evaluaciones del Holter de aplicación clínica, como el método diagnóstico desarrollado por Rodríguez, en el cual se diferencia normalidad de enfermedad y evolución entre ambas con base en el análisis de proporciones de la entropía en el atractor geométrico (23). Del mismo modo, se han desarrollado diagnósticos basados en la morfología celular, como la evaluación de células preneoplásicas y neoplásicas de cuello uterino, donde, del mismo modo que en el presente trabajo, se utilizan medidas fractales junto con conceptos originales, para la diferenciación de estados de normalidad y enfermedad (12). Siguiendo esta perspectiva teórica, en la cual se resuelven problemas experimentales y clínicos a partir de la aplicación de teorías físicas y matemáticas, en el presente trabajo, partiendo de la geometría fractal, se realizaron cuantificaciones estrictas que caracterizan objetivamente el grado de compromiso o normalidad para cualquier ventriculograma.
Estos resultados evidencian que, del mismo modo que ocurre con las teorías físicas desarrolladas en el último siglo (24-26), una concepción acausal de la naturaleza permite el establecimiento de órdenes matemáticos subyacentes a la irregularidad y aparente impredecibilidad de los fenómenos de la medicina, de utilidad no sólo en el campo clínico y experimental sino en el de la salud pública.
Conclusiones- Se desarrolló un nuevo método matemático de evaluación diagnóstica de la ventriculografía izquierda, que caracteriza de manera unificada la estructura y la fisiología ventricular, encontrando que las similitudes entre las dimensiones fractales de los componentes de un ventrículo con fracción de eyección normal, son menores o iguales a 90, mientras que en un ventrículo anormal estas similitudes varían en un rango de 1 a 9.000, presentando un valor mayor que 100 en por lo menos una de las comparaciones.
- Al desarrollar una progresión geométrica de los grados de similitud para las dimensiones fractales, se encontró que los valores mayores a 1 se superponen en los casos leve y moderado, sólo diferenciando los severos por valores mayores a 100 en una de las tres medidas realizadas.
- Con esta nueva metodología es posible cuantificar la evolución entre normalidad y compromiso severo del ventrículo, permitiendo también establecer evolución entre normalidad y enfermedad.
- La precisión de las medidas usadas por esta nueva metodología diagnóstica hace innecesario el uso de medidas estadísticas y permite una evaluación matemática general y objetiva de cualquier ventriculograma en particular.
AgradecimientosA la Fundación Cardioinfantil, en especial a los doctores Darío Echeverri, Cardiólogo de la institución y Rodolfo Dennis, Director del Departamento de Investigaciones, por apoyar este trabajo.
A la Universidad Militar Nueva Granada, en especial a los doctores José Ricardo Cure Hakim, Vicedecano de investigaciones, Henry Acuña, Jefe de la división de Investigación Científica, y Esperanza Fajardo, Directora del Centro de Investigaciones de la Facultad de Medicina.
Al Centro de Investigaciones de la Clínica del Country, en especial a los doctores Andrés Rodríguez, Director del Centro de Investigaciones, Jorge Ospina, Director Médico de la Clínica del Country, y Tito Tulio Roa, Director de Educación Médica, por su apoyo en las investigaciones.
A Jacqueline Romero, Adriana Forero y Doris Páez de la Fundación Cardioinfantil, por su apoyo a las investigaciones del grupo Insight.
Este trabajo es resultado del proyecto MED 736, financiado por el Fondo de investigaciones de la Universidad Militar Nueva Granada.
______
1Por ejemplo, en la tabla 1, en el paciente 6 del grupo leve, el grado de similitud entre las dimensiones fractales de la sístole y la totalidad se calcula así: la primera cifra diferente entre los números está en las centésimas, que en la sístole es 1, mientras en la totalidad es 6; se restan obteniendo 5, lo que se multiplica con el valor asignado a esta cifra significativa que es 100, de lo que resulta que el grado de similitud es 500.
Bibliografía1. Mandelbrot B. The fractal geometry of nature. Barcelona: Tusquets Eds.; 2000. p. 341-8. [ Links ]
2. Peitgen H, Jurgens H, Saupe D. Lenght, area and dimension. Measuring complexity and scaling properties. En: Peitgen H, Jurgens H, Saupe D. Chaos and Fractals: New Frontiers of Science. New York: Springer - Verlag; 1992. p.183-228. [ Links ]
3. Mandelbrot B. ¿Cuánto mide la costa de Bretaña? En: Mandelbrot B. Los Objetos Fractales. Barcelona: Tusquets Eds; 2000. p. 27-50. [ Links ]
4. Pohlman S, Powell K, Obuchowski NA, Chilcote WA, Grundfest - Broniatowski S. Quantitative classification of breast tumours in digitized mammograms. Med Phys. 1996; 23: 1337-1345. [ Links ]
5. Lefebvre F, Benali HA. Fractal approach to the segmentation of microcalcifications in digital mammograms. Med Phys. 1995; 22: 381-390. [ Links ]
6. Landini G, Rippin JW. Fractal dimensions of epithelial-connective tissue interfaces in premalignant and malignant epithelial lesions of the floor of mouth. Anal Quant Cytol Histol. 1993; 15: 144-149. [ Links ]
7. Gazit Y, Baish JW, Safabaksh N. Fractal characteristics of tumour vascular architecture during tumour growth and regression. Microcirculation 1997; 4 (4): 395-402. [ Links ]
8. Rodríguez J, Mariño M, Avilán N, Echeverri D. Medidas fractales de arterias coronarias, un modelo experimental en restenosis, armonía matemática intrínseca de la estructura arterial. Rev Colomb Cardiol 2002;10:65-72. [ Links ]
9. Rodríguez J, Álvarez L, Mariño M, Avilán N, Prieto S, Casadiego E, et al. Variabilidad de la dimensión fractal del árbol coronario izquierdo en pacientes con enfermedad arterial oclusiva severa. Rev Colomb Cardiol. 2004; 11 (4): 185-92. [ Links ]
10. Rodríguez J, Prieto S, Ortiz L, Correa C, Álvarez L, Bernal P, et al. Variabilidad de la dimensión fractal de la ramificación coronaria izquierda en ausencia y presencia de EAO moderada y severa. Rev Colomb Cardiol. 2007; 14 (3): 173-180. [ Links ]
11. Rodríguez J, Prieto S, Correa C, Bernal P, Puerta G, Vitery S, et al. Theoretical generalization of normal and sick coronary arteries with fractal dimensions and the arterial intrinsic mathematical harmony. BMC Med Phys 2010; 10: 1-6. Disponible en: http://www.biomedcentral.com/1756-6649/10/1 [ Links ]
12. Rodríguez J, Prieto S, Ortiz L, Bautista A, Bernal P, Avilán N. Diagnóstico matemático de la monitoria fetal aplicando la ley de Zipf-Mandelbrot. Rev Fac Med Univ Nac Colomb. 2006; 54 (2): 96-107. [ Links ]
13. Rodríguez J, Prieto S, Correa C, Posso H, Bernal P, Puerta G, et al. Generalización fractal de células preneoplásicas y cancerígenas del epitelio escamoso cervical. Una nueva metodología de aplicación clínica. Rev Fac Med. En prensa. [ Links ]
14. Harrison TR. Principios de Medicina Interna. Madrid: Mc Graw Hill; 1998. p. 1429-1430. [ Links ]
15. Rodríguez J, Prieto S, Ortiz L, Avilán N, Álvarez L, Correa C, et al. Comportamiento fractal del ventrículo izquierdo durante la dinámica cardiaca. Rev Colomb Cardiol. 2006; 13 (3): 165-170. [ Links ]
16. Kappenberger L. Arrhythmia: a therapeutic dilemma. En: Virag N, Blanc O, Kappenberger, L. Computer Simulation and Experimental Assessment of Cardiac Electrophysiology. Lausanne: Futura Publishing Company; 2001. p. 185-188. [ Links ]
17. Huikuri HV, Mäkikallio TH, Peng Ch, Goldberger AL, Hintze U, Moller M. Fractal correlation properties of R-R interval dynamics and mortality in patients with depressed left ventricular function after an acute myocardial infarction. Circulation 2000; 101: 47-53. [ Links ]
18. Rodríguez J. Teoría de unión al HLA clase II: teoría de probabilidad, combinatoria y entropía aplicadas a secuencias peptídicas. Inmunología 2008; 27 (4): 151-166. [ Links ]
19. Rodríguez J, Bernal P, Prieto S, Correa C .Teoría de péptidos de alta unión de malaria al glóbulo rojo. Predicciones teóricas de nuevos péptidos de unión y mutaciones teóricas predictivas de aminoácidos críticos. Inmunología 2010; 29 (1). [ Links ]
20. Rodríguez J, Prieto S. Dinámica de la epidemia de malaria. Predicciones de la trayectoria de la epidemia. Rev Fac Med. Aprobado para publicación. [ Links ]
21. Rodríguez J. Método para la predicción de la dinámica temporal de la malaria en los municipios de Colombia. Rev Panam Salud Publica. 2010; 27 (3): 211-8. [ Links ]
22. Goldberger AL, Amaral L, Hausdorff JM, Ivanov P, Peng Ch, Stanley HE. Fractal dynamics in physiology: alterations with disease and aging. PNAS 2002; 99: 2466-2472. [ Links ]
23. Rodríguez J. Entropía proporcional de los sistemas dinámicos cardiacos: predicciones físicas y matemáticas de la dinámica cardiaca de aplicación clínica. Rev Colomb Cardiol 2010; 17: 115-129. [ Links ]
24. Feynman R. Leighton RB, Sands M. Comportamiento cuántico. En: Feynman R. Leighton RB, Sands M. Física. Vol. 1, Cap. 37. Wilmington: Addison-Wesley Iberoamericana S.A.; 1987. [ Links ]
25. Fernández - Rañada A. Movimiento caótico. En: orden y caos. Scientific American. Prensa Científica S.A., 1990. p. 66-77. [ Links ]
26. Feynman R. Los principios de la mecánica estadística. En: Física. Vol. 1. Cap. 40. Addison-Wesley Iberoamericana S.A.; 1987. [ Links ]














