Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Colombiana de Cardiología
Print version ISSN 0120-5633
Rev. Colomb. Cardiol. vol.19 no.5 Bogota Sept./Oct. 2012
Dinámica fractal de la ramificación coronaria izquierda
Fractal dynamic of the left coronary branching
Grupo Insight. Bogotá, Colombia.
(1) Grupo Insight. Bogotá, Colombia.
(2) Universidad Militar Nueva Granada. Bogotá, Colombia.
(3) Centro de Investigaciones Clínica del Country. Bogotá, Colombia.
Correspondencia: Dr. Javier Rodríguez Velásquez. Calle 45 sur No. 78 I-25, Teléfono: (57) 313 405 7252, Bogotá, Colombia. Correo electrónico: grupoinsight2025@yahoo.es
Recibido: 09/11/2011. Aceptado: 12/04/2012.
INTRODUCCIÓN Y OBJETIVOS: la geometría fractal evalúa la irregularidad de los objetos naturales, permitiendo caracterizar de forma imparcial la totalidad de la ramificación coronaria izquierda a diferencia de la metodología actual que evalúa únicamente partes de ésta. Con base en esta medida se generalizó una nueva metodología diagnóstica para detectar cualquier tipo de disfunción cardiaca severa.
MÉTODOS: estudio de concordancia diagnóstica en el que se utilizó el método de box counting para medir dimensiones fractales de imágenes consecutivas entre sístole y diástole de la ramificación coronaria izquierda en proyección oblicua derecha anterior de angiografías de ocho pacientes con enfermedad arterial oclusiva leve. Así mismo, se evaluaron sus cambios por medio de los conceptos de variabilidad y diferencia neta y se compararon estos resultados con pacientes sin enfermedad arterial oclusiva, con enfermedad arterial oclusiva moderada y severa evaluados previamente de igual forma, para obtener una metodología matemática que evalúa el impacto de cualquier patología en la dinámica cardiaca.
RESULTADOS: los casos que presentan diferencias netas de cero corresponden a pacientes con disfunciones cardiacas severas, independientemente del grado o ausencia de enfermedad arterial oclusiva diagnosticada.
CONCLUSIONES: se generalizó una nueva metodología diagnóstica de aplicación clínica que detecta disfunciones cardiacas severas sub-diagnosticadas con las metodologías actuales, mediante la caracterización de la dinámica total de la ramificación coronaria izquierda.
PALABRAS CLAVE: fractal, angiografía, diagnóstico.
INTRODUCTION AND OBJETIVES: fractal geometry evaluates the irregularity of natural objects, allowing impartially characterize the entire left coronary branching unlike the current methodology which evaluates only parts of it. Based on this measure, a new diagnostic method was generalized to detect any type of severe cardiac dysfunction.
METHODS: Concordance study using the box counting method to measure fractal dimensions of consecutive images between systole and diastole of the left coronary branch in right anterior oblique projection in angiograms of eight patients with mild arterial occlusive disease. Likewise, we evaluated its changes through the concepts of variability and net difference and compared these results with patients without occlusive arterial disease, with moderate to severe arterial occlusive disease previously and similarly evaluated, to obtain a mathematical methodology to assess the impact of any pathology in cardiac dynamics.
RESULTS: The cases with zero net differences occur in patients with severe cardiac dysfunction, regardless of the degree or absence of diagnosed occlusive arterial disease.
Conclusions: a new diagnostic methodology of clinical application to detect sub-diagnosed severe heart dysfunction was generalized with current methodologies, through the characterization of the total dynamics of the left coronary branch.
KEYWORDS: fractal, angiography, diagnosis.
Introducción
La geometría fractal, desarrollada por Benoît Mandelbrot, describe matemáticamente objetos irregulares (1). Esta geometría se originó al analizar paradojas que evidenciaban la imposibilidad de realizar caracterizaciones efectivas de objetos irregulares mediante medidas euclidianas (2) y condujo a la definición de dimensión fractal (3). Dada la naturaleza irregular de las estructuras biológicas, la utilización de esta geometría en la investigación médica ha permitido realizar medidas matemáticas objetivas (4-6) y determinar diferencias entre salud y enfermedad con aplicaciones experimentales y clínicas (7-9). Existen diferentes definiciones y metodologías de medición de la dimensión fractal, de acuerdo con las características del objeto a medir (10), las cuales se han aplicado a la caracterización del sistema inmune (11, 12), la morfología cardiaca con implicaciones fisiológicas (7), el desarrollo de diagnósticos de aplicación clínica en la monitoría fetal (13, 14), las células y tejidos (8), así como las discriminaciones entre diferentes estructuras normales y con alteraciones neoplásicas (15-20).
La metodología actual de evaluación clínica de la enfermedad arterial oclusiva con la angiografía, impide ver el impacto de la obstrucción sobre la totalidad de la ramificación y los cambios en su forma durante la dinámica cardiaca. Rodríguez y colaboradores (21) desarrollaron una nueva medida morfométrica de evaluación clínica de angiografías coronarias, basándose en el cálculo de las dimensiones fractales de secuencias de imágenes de la ramificación coronaria izquierda entre sístole y diástole y los conceptos originales de variabilidad y diferencia neta, y encontraron que los pacientes que presentan enfermedad arterial oclusiva severa generalmente se caracterizan por una menor variabilidad en la secuencia de dimensiones fractales evaluada con la diferencia neta, que los pacientes sin enfermedad arterial oclusiva. Esta metodología valora el impacto de la obstrucción respecto al comportamiento global y posteriormente fue aplicada con éxito a pacientes con enfermedad arterial oclusiva moderada (22).
En la presente investigación se aplicará a la enfermedad arterial oclusiva leve la metodología definida en el estudio anterior y se compararán los resultados con los obtenidos previamente para ramificación coronaria izquierda con obstrucción severa, moderada y sin enfermedad arterial oclusiva (21, 22), con el fin de lograr una caracterización matemática general de la misma, desarrollando un diagnóstico matemático de la angiografía aplicable a cualquier disfunción cardiaca.
Métodos
Este es un estudio de concordancia diagnóstica para cuya realización se contó con ocho exámenes de angiografía coronaria con enfermedad arterial oclusiva leve y cálculos previos de siete exámenes de pacientes sin enfermedad arterial oclusiva, 9 de pacientes con enfermedad arterial oclusiva moderada y 7 con enfermedad arterial oclusiva severa (21, 22). Los exámenes fueron hechos en el departamento de Hemodinamia de la Fundación Cardioinfantil, Instituto de Cardiología. La selección y el diagnóstico de los casos fueron efectuados por un especialista de acuerdo con los parámetros utilizados en la clínica en mención (23).
La angiografía coronaria se realizó mediante la canalización de la arteria femoral vía percutánea, y la inserción de catéteres intravasculares (24, 25) para la canulación selectiva del ostium de las arterias coronarias izquierda y derecha y la inyección del medio de contraste. La digitalización y posterior revisión de estas imágenes se hizo a través de un reproductor de imágenes angiográficas Acom T.O.P. marca Siemmens.
Al seguir la metodología previamente desarrollada por Rodríguez y colaboradores (21) basada en el método de box counting, en la que con sólo dos rejillas es posible hacer comparaciones y diferenciaciones físicas efectivas, se superpusieron dos cuadrículas a cada imagen, formadas por cuadros de 1 y 2 cm de lado, respectivamente, y se contó el número de cuadros que ocupaba la ramificación en cada cuadrícula. Con estos datos se calcularon las medidas de dimensión fractal de cada una de las imágenes de la secuencia de sístole a diástole, empleando la ecuación de dimensión fractal de box-counting:
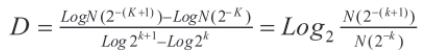
Donde N es el número de cuadros que conforman el objeto irregular; K denota el grado de partición de la cuadrícula y D es la dimensión fractal.
Análisis matemático de las medidas
Para la evaluación de las dimensiones fractales se utilizaron los conceptos de variabilidad y diferencia neta. La variabilidad de la dimensión fractala se define como la variación en las décimas de medidas consecutivas de la dimensión fractal en la totalidad de la secuencia. La diferencia netab es la medida numérica del cambio total creciente y decreciente en una secuencia. El cambio total creciente es la suma del doble de veces que se presenta una variación creciente de dos décimas y el triple de veces que se presenta una variación de tres décimas en la secuencia de dimensiones fractales. Para calcular el cambio total decreciente se utiliza el mismo procedimiento. La diferencia neta es la diferencia entre estos valores (21). Estos conceptos evalúan objetivamente el cambio en la estructura geométrica de la ramificación coronaria izquierda, lo que permite determinar el impacto de cualquier patología en la morfología cardiaca de manera objetiva y reproducible, haciendo innecesario el uso de análisis estadísticos.
Estos resultados fueron comparados con los obtenidos previamente para ramificación coronaria izquierda con lesión severa, moderada y sin enfermedad arterial oclusiva, estableciendo cuatro grupos:
Grupo 1: ausencia de enfermedad arterial oclusiva.
Grupo 2: enfermedad arterial oclusiva leve.
Grupo 3: enfermedad arterial oclusiva moderada.
Grupo 4: enfermedad arterial oclusiva severa.
Para la determinación de características diferenciales entre los grupos evaluados se evaluó conjuntamente el número de diferencias netas de cero en comparación con el resto de valores en los diferentes grupos.
Este estudio se clasifica como investigación sin riesgo ya que se hacen cálculos matemáticos sobre resultados de exámenes clínicos que han sido prescritos médicamente, donde los resultados del trabajo no afectan en modo alguno a los pacientes. Adicionalmente, cumple con las normas científicas, técnicas y administrativas para la investigación en salud, con base en la resolución No. 008430 de 1993, y específicamente con el título 11 referente a la investigación en seres humanos, respetando su integridad y anonimato.
Resultados
Las dimensiones fractales de los cuatro grupos oscilan entre 1,15 y 1,93. Para el grupo 1 están entre 1,31 y 1,84, para el 2 estos valores varían entre 1,30 y 1,77; para el 3 presenta valores entre 1,33 y 1,93 y para el 4 entre 1,15 y 1,82. Estos resultados se muestran en las tablas 1, 2, 3 y 4.
Al observar el comportamiento de las diferencias netas de la variabilidad en los grupos, se evidencia que generalmente para el grupo 1 este valor es diferente de cero, a excepción del paciente 4, mientras que es igual a cero en dos casos del grupo 2, en tres casos del grupo 3 y en cinco del grupo 4, señalando una disminución de la variabilidad al aumentar la gravedad de la lesión, de tal modo que, comúnmente, las lesiones severas se caracterizan por diferencias netas de cero (Tabla 5).
Además, se encuentran algunas simetrías en el grupo 4 en los saltos de 2 ó 3 en la dimensión calculada, evidenciando equivalencias en los cambios creciente y decreciente de los pacientes, comportamiento que no es observable en ningún otro grupo.
Discusión
Este es el primer trabajo donde se generaliza una metodología de diagnóstico matemático del estado morfológico y funcional del corazón que detecta disfunciones cardiacas severas independientemente de la patología presente, con base en dimensiones fractales de imágenes consecutivas entre sístole y diástole de angiografías de arterias coronarias izquierdas. La comparación de casos de enfermedad arterial oclusiva leve con información previa respecto a casos sin enfermedad arterial oclusiva, y con enfermedad arterial oclusiva moderada y severa (21, 22), permitió observar el impacto de la lesión en el funcionamiento total de la ramificación, evidenciando un parámetro matemático característico de lesiones severas independiente de la lesión diagnosticada desde los parámetros convencionales.
Se usaron las definiciones de variabilidad y diferencia neta de las dimensiones fractales como medida morfométrica, y se encontró que la variabilidad evaluada con la diferencia neta generalmente aumenta al disminuir la gravedad de la lesión y disminuye en los casos de enfermedad arterial oclusiva severa, lo que se evidencia en el aumento progresivo de diferencias netas de cero al aumentar la gravedad de la lesión.
La metodología desarrollada, al evaluar la totalidad de la ramificación coronaria y los cambios geométricos que presenta en su movimiento, evalúa el impacto de cualquier patología en la dinámica cardiaca superando las dificultades diagnósticas actuales en los casos en los que no aparece la enfermedad arterial oclusiva, pero sí una diferencia neta de cero evaluada con esta metodología.
En este trabajo se determina matemáticamente la dinámica fractal de la totalidad de la ramificación coronaria izquierda mediante la evaluación del cambio geométrico de su estructura en imágenes consecutivas de su paso de sístole a diástole. Para ello, las dimensiones fractales obtenidas se evaluaron por medio de los conceptos matemáticos de variabilidad y diferencia neta de cada secuencia, que evalúan no sólo el impacto de la obstrucción respecto a la totalidad sino además el cambio de la estructura geométrica en el tiempo durante la dinámica cardiaca, obteniendo una caracterización objetiva de la angiografía independiente del número de mediciones consecutivas tomadas de la misma.
El análisis de las diferencias y similitudes entre los grupos se basa en la observación del comportamiento global del número de diferencias netas de 0 que aparecen en cada grupo, puesto que en ellos se evidencia la disminución de la variabilidad. La presencia de diferencias netas, generalmente de cero en el grupo de pacientes con enfermedad arterial oclusiva severa, permite concluir que este valor es característico de una disfunción cardiaca severa. Cabe anotar que sólo se presentó una diferencia neta de 5 correspondiente a un paciente sin enfermedad arterial oclusiva, lo cual está acorde con los resultados obtenidos, puesto que evidencia una alta variabilidad, generalmente asociada a ausencia de enfermedad arterial oclusiva. La diferencia neta de cero se encontró en distintos casos en todos los grupos, incluyendo ausencia de enfermedad arterial oclusiva, lo que pone en evidencia casos subdiagnosticados desde la metodología tradicional, que podrían ser detectados y contar con un seguimiento más minucioso con la aplicación de esta metodología. Para este tipo de pacientes se recomendaría un mejor seguimiento a fin de precisar pronósticos en la clínica.
La teoría del caos, que analiza fenómenos impredecibles, caracteriza los sistemas con atractores de forma irregular como los fractales, y ha permitido reinterpretar los problemas tradicionales del estudio del corazón de una manera matemática objetiva, en muchos casos con aplicaciones experimentales y clínicas. Durante los últimos veinte años se han desarrollado investigaciones en fisiología cardiaca que invalidan la concepción homeostática tradicional del ritmo cardiaco, demostrando que se trata de una dinámica caótica cuyo estudio permite establecer diferencias entre salud y enfermedad (26-28). Gracias al uso de geometría fractal, Huikuri y colaboradores (29), desarrollaron una medida fractal de los intervalos R-R con la cual estimaron el riesgo de mortalidad en pacientes con fracción de eyección menor al 35% después de un infarto agudo del miocardio, de manera más eficaz que los parámetros clínicos convencionales. Por su parte, Goldberger y colaboradores (30, 31), encontraron que al caracterizar matemáticamente mediante espacios de fase los intervalos entre sístole y diástole, la periodicidad y la aleatoriedad de la dinámica cardiaca están asociadas a enfermedad, mientras que la salud corresponde a un comportamiento intermedio. Rodríguez y colaboradores (13), desde una reinterpretación de la concepción de salud-enfermedad de la Teoría de Sistemas Dinámicos, desarrollaron un método de diagnóstico matemático de la monitoría fetal de aplicación clínica empleando la ley de Zipf-Mandelbrot al análisis de la frecuencia de aparición de los CDS, que posteriormente fue refinado y generalizado (14). También se han aplicado sistemas dinámicos y probabilidades al Holter con implicaciones clínicas (32, 33), y se desarrolló un diagnóstico físico y matemático de aplicación clínica basado en proporciones de la entropía en el atractor geométrico (34), que posteriormente fue aplicado al seguimiento de pacientes en la unidad de Cuidados Coronarios, cuantificando el impacto de intervenciones de tipo farmacológico y/o quirúrgico, y evidenciando procesos de agudización de la dinámica cardiaca, aún sin presentar síntomas clínicos visibles (35). Recientemente se desarrolló una ley de carácter exponencial de la dinámica caótica cardiaca, que establece diferencias diagnósticas entre normalidad, enfermedad y evolución, y cuantifica la totalidad de dinámicas posibles para cada estado (36). Siguiendo una concepción matemática y física, estos trabajos permiten realizar afirmaciones para cada caso particular con base en análisis de la dinámica cardiaca. En la presente investigación se sigue la misma línea teórico-práctica, realizando un análisis geométrico de los cambios durante el movimiento con el cual se obtiene la dinámica fractal de un mismo objeto, que permite detectar disfunciones severas no detectables con las metodologías tradicionales ni con las dimensiones fractales observadas independientemente. La aplicación de conceptos matemáticos hace innecesario el uso de análisis estadísticos, puesto que permiten realizar medidas objetivas y reproducibles.
Dado que la angiografía es un examen invasivo, no es posible caracterizar el funcionamiento de un corazón normal con esta metodología; además, para la realización de esta investigación se ha contado con pacientes que presentan diferentes sintomatologías y patologías como hipertensión arterial o miocardiopatía dilatada, entre otras, además de manifestar enfermedad arterial oclusiva. Estas condiciones dificultan el desarrollo de una metodología que dé cuenta del paso de normalidad a enfermedad; sin embargo, evaluar casos de disfunción cardiaca objetivamente, además de enfermedad arterial oclusiva severa, permite generalizar un parámetro matemático para cualquier disfunción severa de diagnóstico clínico.
La variabilidad de la dimensión fractal proporciona un único número que sintetiza la información de cada secuencia; para su obtención no se tienen en cuenta los cambios en una y cuatro décimas puesto que los primeros aparecen de manera indistinta en los grupos evaluados, y sólo se registra un cambio de cuatro décimas correspondiente a uno de los pacientes del grupo 4.
En la actualidad no existe una metodología que integre la información de los exámenes que evalúan la fisiología y morfología cardiacas. La simulación computacional ha abierto nuevas posibilidades metodológicas para la investigación científica; tal es el caso de las simulaciones de la actividad cardiaca realizadas por Kappenberger que muestran cómo la geometría y la anatomía influyen en la estabilidad eléctrica del corazón (37). Es así como, al hacer uso de estas simulaciones en Medicina, sería posible efectuar una mejor evaluación del paciente a partir del análisis unificado de diferentes exámenes, como ventriculograma, fracción de eyección ventricular, electrocardiogramas, Holter, etc., y otras medidas como la variación geométrica del corazón en movimiento con dimensiones fractales, que brinden un diagnóstico global y objetivo como los realizados en este trabajo.
La aplicación de teorías físicas y matemáticas en campos fundamentales de la Medicina se ha efectuado por ejemplo en Biología molecular, donde se han realizado predicciones como la unión de péptidos de malaria implicados en el proceso de invasión al glóbulo rojo con una especificidad del 90% y una sensibilidad del 95% (38), además de caracterizaciones y predicciones en Inmunología, entre las que se encuentran predicciones de unión de péptidos de malaria (39), que podrían ser útiles para el desarrollo de vacunas. En Salud pública se han desarrollado predicciones anuales en dengue y malaria, así como predicciones de brotes de malaria en tres semanas para 820 municipios de Colombia con una eficacia del 99,86% (40). También se han logrado generalizaciones con implicaciones a nivel clínico y experimental, por ejemplo en células preneoplásicas y neoplásicas de cuello uterino, donde fue posible cuantificar la totalidad de prototipos fractales posibles y establecer un diagnóstico diferencial para cada uno (41); del mismo modo se determinó el número total de posibles estructuras arteriales coronarias en el proceso de estenosis y restenosis, desde normalidad hasta oclusión total de la luz (42).
Las teorías físicas actuales (43-45) se basan en una concepción acausal de la naturaleza, logrando predicciones precisas; en Medicina, siguiendo esta teorización acausal, se logran predicciones de utilidad no sólo en el plano clínico y experimental sino en Salud pública.
Aplicaciones futuras
La aplicación clínica de esta metodología permitirá detectar pacientes subdiagnosticados, sin importar la presencia o ausencia de enfermedad arterial oclusiva, y al seguirlos rigurosamente en el tiempo, aportar acerca de la evolución hacia mayor compromiso cardiaco y probablemente sobre mortalidad. Además, la metodología desarrollada facilitará la realización de simulaciones computacionales del comportamiento cardiaco, así como la construcción de metodologías de evaluación que sinteticen la información de diferentes exámenes como angiografías, ventriculogramas y otros. Sería muy importante correlacionar el diagnóstico desarrollado para el Holter con las proporciones de la entropía con las medidas de las ramificaciones coronarias realizadas en este trabajo.
Conclusiones
La metodología generalizada en este trabajo permite una caracterización diagnóstica objetiva y reproducible de la dinámica total de la ramificación coronaria izquierda observada en angiografías.
El grupo con enfermedad arterial oclusiva severa se caracteriza por presentar generalmente diferencias netas de cero, a diferencia de los otros grupos, evidenciando que este valor constituye un parámetro característico de disfunción severa independientemente de la presencia de enfermedad arterial oclusiva, que permite detectar disfunciones severas subdiagnosticadas.
El uso de teorías matemáticas hace posible obtener resultados concluyentes sin necesidad de un gran volumen poblacional, ni tratamientos estadísticos, lo que optimiza esfuerzos y recursos.
Agradecimientos
Los autores manifiestan su agradecimiento a la Fundación Cardioinfantil - Instituto de Cardiología, en especial a los doctores Darío Echeverri, Cardiólogo de la institución, y Rodolfo Dennis, director del Departamento de Investigaciones, por apoyar este trabajo.
De igual forma, a la Universidad Militar Nueva Granada, en especial a los Doctores Martha Bahamón, Vicerrectora Académica, José Ricardo Cure Hakim, Vicerrector de Investigaciones, Henry Acuña, Jefe de la división de Investigación Científica, Clara Benavides, Directora del Programa de Medicina, y Esperanza Fajardo, Directora del Centro de Investigaciones. Este trabajo es resultado del proyecto MED 842 financiado por el Fondo de investigaciones de la Universidad Militar Nueva Granada.
Y, finalmente, al Centro de Investigaciones de la Clínica del Country por su apoyo a nuestras investigaciones, en especial a los Drs. Andrés Rodríguez, director del Centro de Investigaciones y subdirector médico de la institución y Adriana Lizbeth Ortiz, epidemióloga del Centro, por el apoyo a las investigaciones.
Bibliografía
1. Mandelbrot B. Introducción. Los objetos fractales. Barcelona: Tusquets Eds S.A.; 2000. p. 13-26. [ Links ]
2. Mandelbrot B. ¿Cuánto mide la costa de Bretaña? Los objetos fractales. Barcelona: Tusquets Eds. S.A.; 2000. p. 27-50. [ Links ]
3. Mandelbrot B. The fractal geometry of nature. San Francisco: Freeman; 1972. p. 341-348. [ Links ]
4. West JW. Fractal physiology and chaos in Medicine. Singapore: World Scientific; 1990. [ Links ]
5. Goldberger AL, West BJ. Fractals in Physiology and Medicine. Yale: Journal Biol 1987; 60: 421-35. [ Links ]
6. Glenny H, Robb W, Robertson H, Thomas, Yamashiro, Stanley, et al. Applications of fractal analysis to physiology. J Appl Phys. 1991; 70 (6): 2351-2367. [ Links ]
7. Rodríguez J, Mariño M, Avilán N, Echeverri D. Medidas fractales de arterias coronarias en un modelo experimental de restenosis. Armonía matemática intrínseca de la estructura arterial. Rev Col Cardiol 2002; 10: 65-72. [ Links ]
8. Baish JW, Jain RK. Fractals and cancer. Cancer research 2000; 60: 3683-3688. [ Links ]
9. Dey P, Rajesh L. Fractal dimension in endometrial carcinoma. Anal Quant Cytol Histol 2004; 26 (2): 113-6. [ Links ]
10. Peitgen H, Jurgens H, Saupe D. Chaos and Fractals: New Frontiers of Science. N.Y.: Springer-Verlag; 1992. p. 202-219. [ Links ]
11. Burgos J. Fractal representation of the immune B cell repertoire. Biosystems 1996; 39: 19-24. [ Links ]
12. Burgos J, Moreno-Tovar P. Zipf-scaling behavior in the immune system. Biosystems 1996; 39: 227-232. [ Links ]
13. Rodríguez J, Prieto S, Ortiz L, Bautista A, et al. Diagnóstico matemático de la monitoría fetal aplicando la ley de Zipf-Mandelbrot. Rev Fac Med Univ Nac Colomb 2006; 54 (2): 96-107. [ Links ]
14. Rodríguez J. Dynamical systems theory and ZIPF - Mandelbrot Law applied to the development of a fetal monitoring diagnostic methodology. XVIII FIGO world congress of gynecology and obstetrice. Kuala Lumpur, Malaysia. November 2006. [ Links ]
15. Gazit Y, Berk DA, Leunig M. Scale-invariant behavior and vascular network formation in normal and tumor tissue. Phys Rev Lett 1995; 75: 2428-243. [ Links ]
16. Gazit Y, Baish JW, Safabaksh N. Fractal characteristics of tumor vascular architecture during tumor growth and regression. Microcirculation 1997; 4: 395-402. [ Links ]
17. Pohlman S, Powell K, Obuchowski NA. Quantitative classification of breast tumors in digitized mammograms. Med Phys 1996; 23: 1337-1345. [ Links ]
18. Lefebvre F, Benali H. A fractal approach to the segmentation of microcalcifications in digital mammograms. Med Phys 1995; 22: 381-390. [ Links ]
19. Landini G, Rippin JW. Fractal dimensions of epithelial-connective tissue interfaces in premalignant and malignant ephitelial lesions of the floor of mouth. Anal Quant Cytol Histol 1993; 15: 144-149. [ Links ]
20. Luzi P, Bianciardi G, Miracco C, Desanti MM, Del Vecchio MT, Alia L, et al. Fractal analysis in human pathology. Ann NY Acad Sci 1999; 879: 255-257. [ Links ]
21. Rodríguez J. Álvarez L. Mariño M. Avilán N. Prieto S. Casadiego E. et al. Variabilidad de la dimensión fractal del árbol coronario izquierdo en pacientes con enfermedad arterial oclusiva severa. Dinámica fractal de la ramificación coronaria. Rev Col Cardiol 2004; 11 (4): 185-92. [ Links ]
22. Rodríguez J, Prieto S, Ortiz L, Correa C, Álvarez L, Bernal P, Casadiego E. Variabilidad de la dimensión fractal de la ramificación coronaria izquierda en ausencia y presencia de enfermedad arterial oclusiva moderada y severa. Rev Colomb Cardiol 2007; 14 (3): 173-180. [ Links ]
23. Bam D, Brossman W. Diagnostic Cardiac Catheterization and Angiography. En: Kasper D, Braunwald E, Hauser S, Longo D, Jameson JL, Fauci A. Harrison's Principles of Internal Medicine. 16th ed. USA: MacGraw-Hill, 2005. p. 1327-1333. [ Links ]
24. Serrano P, Portero M, Aguarón V, Peleato A, Ferreira I. Cateterismo cardíaco y procedimientos intervencionistas. Clin Invest Arterioscl 2002; 14(3): 156-65. [ Links ]
25. Braunwald, E. Heart disease. Vol. 1. 5a. Ed. Philadelphia Pennsylvania: W.B. Saunders Company. 1997. p. 266-268. [ Links ]
26. Garfinkel A, Spano M, Ditto W, Weiss J. Controlling Cardiac Chaos. Science 1992; 257 (28): 1230-1235. [ Links ]
27. Goldberger AL, Non-linear dynamics for clinicians: chaos theory, fractals, and complexity at the bedside. Lancet 1996; 347: 1312-1314. [ Links ]
28. Plamen I, Rosenblum M, Peng CK, Mietus J, Havlin S, Stanley H, et al. Scaling behavior of heartbeat Intervals obtained by wavelet-based time-series analysis. (Letters to Nature) Nature 1996; 383 (26): 323-327. [ Links ]
29. Huikuri HV, Makikallio TH, Peng Ch, Goldberger AL, Hintze U, Moller M. Fractal correlation properties of R-R interval dynamics and mortality in patients with depressed left ventricular function after an acute myocardial infarction. Circulation 2000; 101: 47-53. [ Links ]
30. Goldberger A, Amaral L, Hausdorff JM, Ivanov P, Peng Ch, Stanley HE. Fractal dynamics in physiology: alterations with disease and aging. PNAS 2002; 99: 2466-2472. [ Links ]
31. Goldberger A, Rigney D, West B. Chaos and fractals in human physiology. Sci Am 1990; 262: 42-49. [ Links ]
32. Rodríguez J, Prieto S, Bernal P, Soracipa Y, Salazar G, Isaza D, et al. Nueva metodología de ayuda diagnóstica de la dinámica geométrica cardiaca. Dinámica cardiaca caótica del Holter. Rev Acad Colomb Cienc 2011; 35 (134): 5-12. [ Links ]
33. Rodríguez J, Correa C Ortiz L, Prieto S, Bernal P, Ayala J. Evaluación matemática de la dinámica cardiaca con la teoría de la probabilidad. Rev Mex Cardiol 2009; 20 (4): 183-9. [ Links ]
34. Rodríguez J. Entropía proporcional de los sistemas dinámicos cardiacos: predicciones físicas y matemáticas de la dinámica cardiaca de aplicación clínica. Rev Colomb Cardiol 2010; 17: 115-129. [ Links ]
35. Rodríguez J, Prieto S, Bernal P, Izasa D, Salazar G, Correa C, et al. Entropía proporcional aplicada a la evolución de la dinámica cardiaca. Predicciones de aplicación clínica. En: La emergencia de los enfoques de la Complejidad en América Latina. Argentina: Comunidad de Pensamiento Complejo (CPC). 2011. En Prensa. [ Links ]
36. Rodríguez J. Mathematical law of chaotic cardiac dynamic: Predictions of clinic application. J Med Med Sci 2011; 2: 1050-1059. [ Links ]
37. Kappenberger L. Arrythmia: a therapeutic dilemma. In: computer simulation and experimental assessment of cardiac electrophysiology. Lausanne: Futura Publishing Company; 2001. p. 185-188. [ Links ]
38. Rodríguez J, Bernal P, Prieto S, Correa C .Teoría de péptidos de alta unión de malaria al glóbulo rojo. Predicciones teóricas de nuevos péptidos de unión y mutaciones teóricas predictivas de aminoácidos críticos. Inmunología 2010; 29 (1): 7-19. [ Links ]
39. Rodríguez J, Bernal P, Álvarez L, Pabón S, Ibáñez S, Chapuel N, et al. Predicción de unión de péptidos de MSP-1 y EBA-140 de plasmodium falciparum al HLA clase II Probabilidad, combinatoria y entropía aplicadas a secuencias peptídicas. Inmunología 2010; 29 (3): 91-99. [ Links ]
40. Rodríguez J. Método para la predicción de la dinámica temporal de la malaria en los municipios de Colombia. Rev Panam Salud Publica 2010; 27 (3): 211-8. [ Links ]
41. Rodríguez J, Prieto S, Correa C, Posso H, Bernal P, Puerta G, et al. Generalización fractal de células preneoplásicas y cancerígenas del epitelio escamoso cervical. Una nueva metodología de aplicación clínica. Rev Fac Med 2010; 18 (2): 173-181. [ Links ]
42. Rodriguez J, Prieto S, Correa C, Bernal P, Puerta G, Vitery S, et al. Theoretical generalization of normal and sick coronary arteries with fractal dimensions and the arterial intrinsic mathematical harmony. BMC Medical Physics 2010; 10: 1-6. [ Links ]
43. Feynman R, Leighton RB, Sands M. Comportamiento cuántico. En: Feynman R. Leighton RB, Sands M. Física. Vol 1. Wilmington: Addison-Wesley Iberoamericana S.A.; 1987. Cap. 37. [ Links ]
44. Fernández - Rañada A. Movimiento caótico. En: orden y caos. Scientific American. Prensa Científica S.A., 1990. p. 66-77. [ Links ]
45. Feynman R. Los principios de la mecánica estadística. En: Feynman R. Leighton RB, Sands M. Física. Vol. 1. Wilmington: Addison-Wesley Iberoamericana S.A.; 1987. Cap 40. [ Links ]













