Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Colombiana de Cardiología
Print version ISSN 0120-5633
Rev. Colomb. Cardiol. vol.20 no.4 Bogota July/Aug. 2013
(1) Centro de investigación, innovación, desarrollo y transferencia de tecnología. Facultad de Ingeniería. Universidad de Caldas. Manizales, Colombia.
(2) Departamento de informática y computación. Universidad Nacional de Colombia. Manizales, Colombia.
(3) Departamento de Lenguajes y Sistemas Informáticos. Universidad Pontificia de Salamanca. Madrid, España.
(4) Facultad de Ingeniería. Universidad de Lomas de Zamora. Buenos Aires, Argentina.
Correspondencia: Dr. Andrés P. Castaño, Universidad de Caldas. Facultad de Ingeniería. Calle 65 No. 26-10. Ci2dt2. Manizales, Colombia. Correo electrónico: andres.castano@ucaldas.edu.co
Recibido: 02/11/2012. Aceptado: 26/02/2013.
Objetivo: evaluar el grado de predictibilidad entre dos modelos de electrofisiología celular para aurícula humana, analizando las propiedades, a nivel tisular, de la duración del potencial de acción (APD) y velocidad de conducción (CV) en un tejido en tres dimensiones incorporando el direccionamiento de fibras para toda la anatomía auricular.
Métodos: se implementaron los modelos celulares de Courtemanche-Ramírez-Nattel y Nygren; además se desarrolló un modelo geométrico detallado y realista de una aurícula humana, partiendo del modelo burdo de Harrild-Henriquez al que se le incorporó el direccionamiento de fibras en toda la anatomía auricular.
Resultados: las constantes de difusión implementadas permitieron obtener en ambos modelos velocidades de conducción muy similares a las velocidades de conducción reales; además, en las regiones de alta conductividad el direccionamiento de fibras longitudinal permitió obtener velocidades de conducción más altas que en otras zonas de la aurícula.
Conclusiones: la curva del potencial de acción muestra un APD90 (AP al 90% de la repolarización) de 320 ms en NYG y 235 ms en CRN. En condiciones donde las propiedades de la membrana no han cambiado en la aurícula normal, se ha observado que en ambos modelos se generan subidas de potencial de acción rápidas que se aprecian en la forma del potencial, asociados con una baja velocidad de propagación en la dirección transversal y una subida lenta del potencial de acción, que se relaciona también con una alta velocidad de propagación en el sentido longitudinal.
Palabras clave: potencial de acción, anisotropía, velocidad de conducción.
Objective: to evaluate the degree of predictability between two models of human atrial cellular electrophysiology, analyzing at tissue level the properties of the action potential duration (APD) and conduction velocity (CV) in a three-dimensional tissue incorporating direction of fibers for the entire atrial anatomy.
Methods: we implemented the cellular models of Courtemanche-Ramirez-Nattel and Nygren, also developed a detailed and realistic geometric model of a human atrium, starting from the clumsy model of Harrild-Henriquez to which we incorporated the direction of fibers throughout the entire atrial anatomy.
Results: The diffusion constants implemented allowed to obtain in both models conduction velocities very similar to the real conduction velocities; moreover, in the high conductivity regions the longitudinal fiber direction allowed to obtain conduction velocities higher than in other areas of the atrium.
Conclusions: the action potential curve shows a APD90 (AP at 90% of repolarization) of 320 ms in NYG and 235 ms in CRN. Under conditions where the membrane properties have not changed in the normal atrium, we observed that in both models increases of fast action potential are generated, which can be seen as the potential associated with a low propagation velocity in the transversal direction and a slow rise of the action potential, which is also related to a high propagation velocity in the longitudinal direction.
Keywords: action potential, anisotropy, conduction velocity.
Introducción
Los modelos computacionales de tejido cardiaco han generado gran cantidad de información acerca de la complejidad de las interacciones entre las propiedades de la membrana y la heterogeneidad estructural del corazón. La fortaleza de los modelos computacionales, radica en que proporcionan una plataforma versátil para que los investigadores puedan interpretar datos experimentales y realizar nuevas predicciones sobre hipótesis que no son observables o comprobables usando las técnicas experimentales actuales. En la clínica, hacen incursión los modelos matemáticos ya que permiten el desarrollo de técnicas especializadas en cirugía asistida. El uso de modelos electro-anatómicos ha permitido también el estudio de fármacos y su efectividad frente a patologías bien identificadas.
La mayoría de los modelos utilizados se basa en estudios previos de propagación en anatomías simplificadas en dos dimensiones sobre las que se ha probado la propagación del potencial de acción estimulando ciertas regiones.
En este trabajo se hace énfasis en dos modelos de electrofisiología celular para aurícula humana, (1) modelo NYG y (2) modelo CRN, ambos desarrollados usando las variables de compuerta estilo Hodgkin-Huxley. El modelo de Nygren usa 29 variables y 12 corrientes de membrana, mientras que el de Courtemanche tiene 21 variables y 12 corrientes de membrana.
La propagación del potencial de acción a nivel celular puede obtenerse a partir de una corriente de estímulo con magnitud y duración suficientes para elevar el potencial de membrana por encima de su umbral de excitabilidad. A nivel tisular, se presentan varios factores adicionales que deben considerarse y hacen este proceso más complejo: velocidad de conducción, anisotropía y curvatura del frente de onda para cada región (3). Los estudios que se encuentran entre estos modelos han sido tratados en detalle para miocitos aislados (4-6). A nivel de tejido, algunos estudios han demostrado que los efectos electrotónicos pueden alterar el comportamiento de la célula aislada y es necesario considerar nuevas propiedades en el tejido, como la propagación y las reentradas, que no se pueden predecir desde la célula aislada (7). Estudios recientes (8) analizan el efecto de la heterogeneidad y anisotropía del tejido en el inicio y mantenimiento de la fibrilación auricular (AF) usando el modelo CRN.
El objetivo de este trabajo es evaluar el grado de predictibilidad entre los dos modelos indicados, analizando las propiedades, a nivel tisular, de la duración del potencial de acción (APD) y velocidad de conducción (CV) en un modelo de tejido realista en tres dimensiones, incorporando el direccionamiento de fibras para toda la anatomía auricular.
Este modelo computacional en 3D puede usarse para estudiar patrones de conducción auricular y los mecanismos que subyacen la génesis de la fibrilación auricular asociada con la heterogeneidad anatómica auricular y su anisotropía. Una aproximación realista de la electrofisiología y la anatomía en nuestro modelo contribuye a comprender la propagación del frente de onda durante un ritmo sinusal normal y la aparición de actividad focal que desencadena la fibrilación auricular, muy común en la clínica.
Métodos
Implementación de los modelos
Los modelos básicos de NYG y CRN fueron implementados y descritos por Nygren y colaboradores (1) y Coutermanche y colaboradores (2, 9) respectivamente, para reproducir la actividad eléctrica celular. Para el modelo de NYG, el valor del parámetro KCa fue modificado a 0,025 mmol/L.
Modelo anatómico auricular
Se desarrolló un modelo geométrico detallado y realista de aurícula humana, partiendo del modelo burdo de Harrild y colegas (10). Los datos originales de esta malla fueron obtenidos de la firma Viewpoint digital, que a su vez los obtuvo de IMR (imágenes de resonancia magnética). Se ajustó el modelo original y se trasladó a un formato estereolitográfico (stl), con el fin de manipular adecuadamente el modelo con el uso de un software de diseño asistido por computador.
Mediante un proceso de remallado se reconvirtió el elemento triangular a un cuadrilátero; a través de un refinado de la malla se agregaron nuevos elementos y se ajustó la superficie a la anatomía natural, sometiéndola a la extrusión para darle volumen. La malla se mejoró redimensionando la geometría a las características anatómicas del tejido auricular siguiendo la observación y el detalle descrito en diversos estudios experimentales y por observación de corazones in vitro.
El modelo anatómico tridimensional obtenido incluye ambas aurículas en las cuales se destaca: el nodo sino-auricular (SAN), la cresta terminalis (CT), el haz intercaval, los músculos pectíneos, el septum spurium, la fosa oval y su anillo, el septum interauricular, el haz de Bachmann, las aurículas izquierda y derecha, la orejuela derecha e izquierda, las venas pulmonares derechas e izquierdas, el istmo, las venas cavas superior e inferior, el vestíbulo de la válvula tricúspide y el de la válvula mitral, así como el seno coronario.
Direccionamiento de fibras
El método utilizado se basa en estudios previos (11) para separar regiones del tejido cuyo direccionamiento de fibras es uniforme. Una vez definida la región, se determina la dirección del vector local de la fibra, considerando el efecto de la curvatura del tejido. Para ello, fue necesario crear un cilindro imaginario que envolviera ese tejido, en cuyo caso se traza una directriz como eje del cilindro imaginario, la cual es una línea en el espacio lo suficientemente separada del tejido como para que lo envuelva. Las líneas tangentes del cilindro corresponden a las fibras del tejido.
Propiedades de conducción
En este modelo se consideraron tres regiones para conductividad alta, media y baja. Las regiones de conductividad alta correspondieron al haz de Bachmann, la cresta terminalis y los músculos pectíneos; las de baja conductividad a la región del istmo y del SAN, y las demás regiones se tomaron como de conductividad media. La región de la fosa oval se consideró no conductora.
Las constantes de difusión del tejido se establecieron de manera que la velocidad de conducción estuviera de acuerdo con los datos experimentales (12, 13). Los valores del tensor de difusión obtenidos para ambos modelos fueron de 0,6 para conductividad alta, 0,2 para conductividad media y 0,1 para conductividad baja. Para ambos modelos la anisotropía se fijó de acuerdo con la relación entre la velocidad de propagación longitudinal y transversal y fue de 10:1 en la cresta terminalis y de 3:1en el resto del tejido auricular. La dirección longitudinal siguió el camino preferente de la dirección de las fibras del tejido.
Métodos numéricos
Una formulación monodominio representa adecuadamente la propagación en un tejido y se indica mediante la siguiente ecuación diferencial
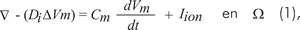
Donde Vm representa el potencial en el espacio intracelular, dt es el tensor de conductividad anisotrópico, Cm la capacitancia de la membrana celular e Iion corresponde al conjunto de corrientes que describen el estado iónico de las células en el tejido como una función del tiempo y de las concentraciones iónicas. Se asume un espacio extracelular con resistencia infinita.
Con las siguientes condiciones de frontera:

Donde n es el vector normal a la superficie.
Esta ecuación corresponde a un modelo de reacción difusión y para resolverlo se desprende un sistema de ecuaciones lineales con un término reactivo altamente no lineal representado por el Iion, que se resolvió mediante el desarrollo de un código en paralelo usando el método de los elementos finitos (FEM). El sistema que ha de resolverse en cada paso de tiempo tiene como número de incógnitas el número de nodos (100554).
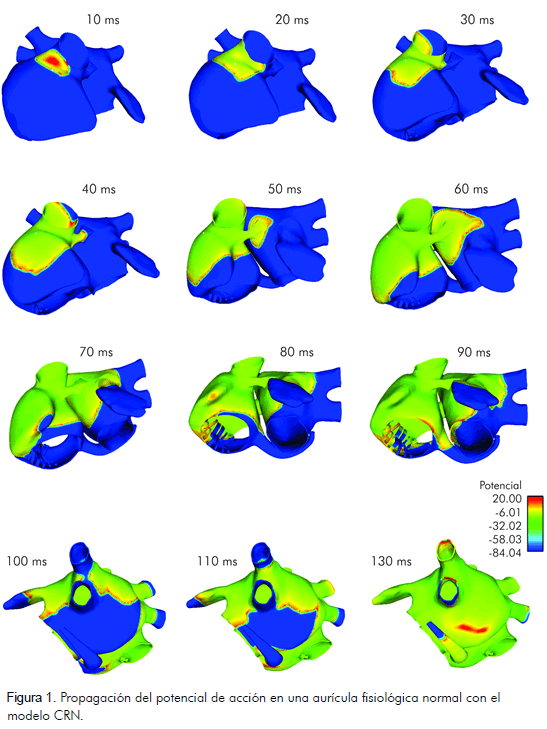
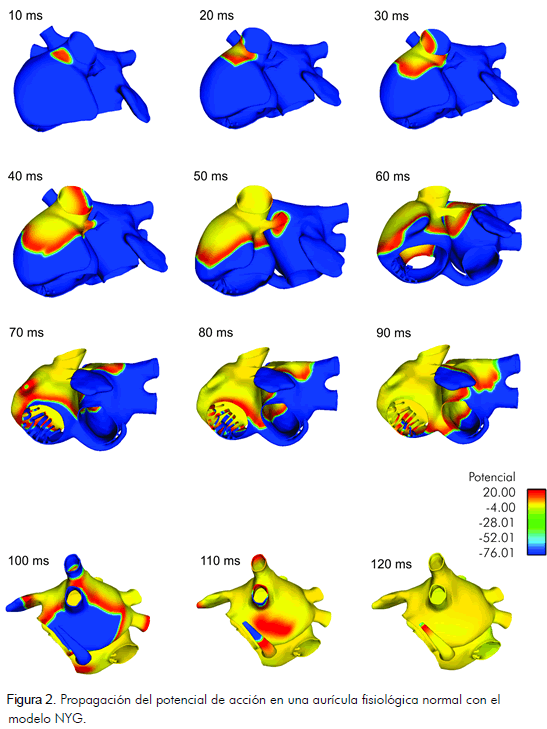
Para estabilizar el tejido se disparó un tren de diez impulsos a una frecuencia de 1 Hz, en la región del SAN con una longitud básica del ciclo (BCL) de un segundo a una frecuencia de 1 Hz y una duración de 6 ms. La propagación para el décimo impulso se muestra en las figuras 1 y 2.
Resultados
La excitación se inicia en el SAN y se expande por la aurícula derecha bifurcándose. Un frente se dirige hacia la cresta terminalis avanzando más rápidamente ya que ésta tiene mayor conductividad, y de allí sigue el camino preferente del haz intercaval en dirección a la región atrioventricular, 30 ms en el modelo de Nygren y 40 ms en el modelo CRN.
Como puede observarse, el frente de onda sigue la dirección hacia la aurícula izquierda con mayor velocidad en la simulación con el modelo de Nygren alcanzando el haz de Bachmann a los 22 ms y lo cruza completamente a los 39 ms, mientras que para CRN se tienen 29 y 45 ms respectivamente.
La región septal se alcanza a los 43 ms (N) y 46 ms (CRN). El cruce se hace más rápido debido a que el haz de Bachmann tiene un direccionamiento de fibra longitudinal y mayor conductividad.
A través de las uniones intermedias, se produce el cruce completo del frente de onda por el anillo de la fosa oval, tardando unos 8 ms (N) y 31 ms (CRN). Hacia la parte inferior el frente propaga más rápidamente siguiendo el camino de la cresta terminalis formando una cola refractaria. La cresta terminalis se cubrió a los 56 ms para N y 68 ms para CRN.
El apéndice derecho se activa completamente a los 75 ms para N y 80 ms para CRN, al tiempo que un nuevo frente inicia el descenso por la pared posterior de la aurícula izquierda y otro se dirige hacia la válvula mitral por la pared izquierda del septum.
El apéndice izquierdo se activa completamente en 112 ms para N y 128 ms para CRN. La última activación de la pared lateral posterior de la aurícula izquierda, se presenta a los 127 ms para N y a los 130 ms para CRN.
El tiempo total de activación de la aurícula derecha fue de 95 ms en N y 110 ms en CRN, y la última región en activarse fue el istmo, que es una región de más baja conductividad.
Durante la propagación se puede ver que los músculos pectíneos son alcanzados en el modelo N a los 24 ms y a los 28 ms en el CRN; además, para ambos modelos se observa que el frente de onda avanza casi a la misma velocidad que el tiempo que tarda el frente dentro de los músculos para cruzarlos.
Las características anatómicas influyen notablemente ya que la propagación sigue los caminos de los grandes haces. Los apéndices auriculares pueden ser más largos en diversos especímenes. Según Gong y colaboradores (14), en esta región se presenta la convergencia de tres frentes de onda, coincidiendo con los resultados observados en el modelo en donde tres frentes de onda se aproximan en este tejido. En nuestro modelo un frente aparece aproximándose desde la región comprendida entre las venas pulmonares izquierdas, otro desde la parte superior de la pared posterior y otro desde la unión interauricular del seno coronario, el cual se ha mezclado con un nuevo frente proveniente de las venas pulmonares derechas (Figuras 1 y 2).
Velocidades de conducción
La velocidad de conducción del frente de onda se midió tomando un punto p1 al que llega el frente de onda y otro punto p2 situado en la perpendicular a la tangente del frente de onda que pasa por p1, buscando que ambos puntos puedan tomarse directamente de los nodos en el modelo. Para el cálculo de ?t se tomó la ocurrencia de máxima potencia en cada punto (Tabla 1).
Debido a que en nuestros modelos se estableció un direccionamiento de fibras longitudinal en el haz de Bachmann y en la cresta terminalis, la velocidad en estas regiones es alta y el frente durante la propagación en la cresta terminalis tiene forma de cono con la punta en dirección hacia la vena cava inferior, demostrándose de esta manera que la velocidad en esta región es más alta que en las demás dentro de la aurícula derecha.
Conclusiones
Las velocidades de conducción obtenidas para las diferentes regiones de la aurícula se encuentran en el rango de las velocidades de conducción de estudios experimentales (20) y simulación (21, 22). Se alcanza la activación completa de la aurícula en 144 ms para NYG y 148 ms para CRN; la última activación ocurre en la parte inferior de la aurícula izquierda a los 126 ms para NYG y 132 ms para CRN y un tiempo de repolarización total de 320 ms para NYG y 345 ms para CRN.
En condiciones donde las propiedades de la membrana no han cambiado en la aurícula normal, se ha observado morfología diferencial del potencial de acción, incrementos rápidos asociados con una baja velocidad de propagación en la dirección transversal e incremento lento, que se asocia también con alta velocidad de propagación en el sentido longitudinal (23).
La curva del potencial de acción muestra un APD90 (AP al 90% de la repolarización) de 320 ms en NYG y 235 ms en CRN.
Las diferencias entre los dos modelos pueden deberse a la heterogeneidad espacial presente de forma nativa en la aurícula humana; además hay otras propiedades que realzan estas diferencias, como los efectos de la edad y el género (24, 25). Sin embargo, en ambos modelos, las corrientes formuladas desde los datos celulares de la aurícula humana representan, en alto grado, una aproximación a los mismos datos experimentales, asumiendo entonces que las diferencias se pueden encontrar en el desarrollo de cada modelo, como es el caso del manejo del calcio intracelular. Ambos modelos han dado resultados dentro del rango esperado en el ámbito experimental; no obstante, factores que corresponden con las características propias del material del tejido, varían en la estabilidad de la señal obtenida.
Implicaciones clínicas
Este trabajo muestra el impacto del uso de modelos para el estudio del ritmo sinusal y la posibilidad de utilizarlos en los estudios patológicos que conduzcan a orientar en la clínica la utilización de cirugía asistida, como se ha sugerido en estudios con modelos computacionales para acertar en la ablación auricular. Así mismo, permite observar y seguir la propagación del frente de onda en condiciones fisiológicas.
Agradecimientos
Un agradecimiento especial por el apoyo del Instituto para la investigación, innovación en Bioingeniería de la Universidad Politécnica de Valencia (España) y al Centro de investigación, innovación, desarrollo y transferencia de tecnología (Ci2dt2) de la Universidad de Caldas (Colombia).
Bibliografía
1. Nygren A, Fiset C, Firek L, Clark JW, Lindblad DS, Clark RB, et al. Mathematical model of an adult human atrial cell: the role of K+ currents in repolarization. Circ Res. 1998; 82 (1): 63-81. [ Links ]
2. Courtemanche M, Ramirez RJ, Nattel S. Ionic mechanisms underlying human atrial action potential properties: insights from a mathematical model. Am J Physiol. 1998; 275 (1 Pt 2): H301-21. [ Links ]
3. Clayton RH, Bernus O, Cherry EM, Dierckx H, Fenton FH, Mirabella L, et al. Models of cardiac tissue electrophysiology: progress, challenges and open questions. Prog Biophys Mol Biol. 2011; 104 (1-3): 22-48. [ Links ]
4. Nygren A, Leon L, Giles W. Simulations of the human atrial action potential. Philosophical Transactions of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences. 2001; 359 (1783): 1111-25. [ Links ]
5. Krogh-Madsen T, Abbott GW, Christini DJ. Effects of electrical and structural remodeling on atrial fibrillation maintenance: a simulation study. PLoS Comput Biol. 2012; 8 (2): e1002390. [ Links ]
6. Cherry EM, Hastings HM, Evans SJ. Dynamics of human atrial cell models: restitution, memory, and intracellular calcium dynamics in single cells. Prog Biophys Mol Biol. 2008; 98 (1): 24-37. [ Links ]
7. Cherry EM, Evans SJ. Properties of two human atrial cell models in tissue: restitution, memory, propagation, and reentry. J Theor Biol. 2008; 254 (3): 674-90. [ Links ]
8. Dongdong Deng Dongdong D, Ling Xia Ling X. Study the effect of tissue heterogeneity and anisotropy in atrial fibrillation based on a human atrial model. Computers In Cardiology Proceedings. 2010: 433-6. [ Links ]
9. Courtemanche M, Ramirez RJ, Nattel S. Ionic targets for drug therapy and atrial fibrillation-induced electrical remodeling: insights from a mathematical model. Cardiovasc Res. 1999; 42 (2): 477-89. [ Links ]
10. Harrild D, Henriquez C. A computer model of normal conduction in the human atria. Circ Res. 2000; 87 (7): E25-36. [ Links ]
11. Ruiz-Villa CA. Estudio de la vulnerabilidad a reentradas a través de modelos matemáticos y simulación de la aurícula humana [Doctoral Thesis]. Valencia: Universitat Politécnica de Valencia; 2011. [ Links ]
12. Hassankhani A, Yao B, Feld GK. Conduction velocity around the tricuspid valve annulus during type 1 atrial flutter: defining the location of areas of slow conduction by three-dimensional electroanatomical mapping. J Interv Card Electrophysiol. 2003; 8 (2): 121-7. [ Links ]
13. Shinagawa K, Mitamura H, Takeshita A, Sato T, Kanki H, Takatsuki S, et al. Determination of refractory periods and conduction velocity during atrial fibrillation using atrial capture in dogs: direct assessment of the wavelength and its modulation by a sodium channel blocker, pilsicainide. J Am Coll Cardiol. 2000; 35 (1): 246-53. [ Links ]
14. Gong Y, Xie F, Stein KM, Garfinkel A, Culianu CA, Lerman BB, et al. Mechanism underlying initiation of paroxysmal atrial flutter/atrial fibrillation by ectopic foci: a simulation study. Circulation. 2007; 115 (16): 2094-102. [ Links ]
15. Boineau JP. Atrial flutter: a synthesis of concepts. Circulation. 1985; 72 (2): 249-57. [ Links ]
16. Hansson A, Holm M, Blomstrom P, Johansson R, Luhrs C, Brandt J, et al. Right atrial free wall conduction velocity and degree of anisotropy in patients with stable sinus rhythm studied during open heart surgery. Eur Heart J. 1998; 19 (2): 293-300. [ Links ]
17. Kojodjojo P, Kanagaratnam P, Segal OR, Hussain W, Peters NS. The effects of carbenoxolone on human myocardial conduction: a tool to investigate the role of gap junctional uncoupling in human arrhythmogenesis. J Am Coll Cardiol. 2006; 48 (6): 1242-9. [ Links ]
18. Hayashi H, Lux RL, Wyatt RF, Burgess MJ, Abildskov JA. Relation of canine atrial activation sequence to anatomic landmarks. Am J Physiol. 1982; 242 (3): H421-8. [ Links ]
19. Cabrera JA, Sanchez-Quintana D, Ho SY, Medina A, Anderson RH. The architecture of the atrial musculature between the orifice of the inferior caval vein and the tricuspid valve: the anatomy of the isthmus. J Cardiovasc Electrophysiol. 1998; 9 (11): 1186-95. [ Links ]
20. Lemery R, Birnie D, Tang ASL, Green M, Gollob M, Hendry M, et al. Normal Atrial Activation and Voltage During Sinus Rhythm in the Human Heart: An Endocardial and Epicardial Mapping Study in Patients with a History of Atrial Fibrillation. J Cardiovasc Electrophysiol. 2007; 18 (4): 402-8. [ Links ]
21. Jacquemet V, Virag N, Ihara Z, Dang L, Blanc O, Zozor S, et al. Study of unipolar electrogram morphology in a computer model of atrial fibrillation. J Cardiovasc Electrophysiol. 2003; 14 (10 Suppl): S172-9. [ Links ]
22. Cox JL, Canavan TE, Schuessler RB, Cain ME, Lindsay BD, Stone C, et al. The surgical treatment of atrial fibrillation. II. Intraoperative electrophysiologic mapping and description of the electrophysiologic basis of atrial flutter and atrial fibrillation. J Thorac Cardiovasc Surg. 1991; 101 (3): 406-26. [ Links ]
23. Spach MS, Miller WT, Miller-Jones E, Warren RB, Barr RC. Extracellular potentials related to intracellular action potentials during impulse conduction in anisotropic canine cardiac muscle. Circ Res. 1979; 45 (2): 188-204. [ Links ]
24. Jeck CD, Boyden PA. Age-related appearance of outward currents may contribute to developmental differences in ventricular repolarization. Circ Res. 1992; 71 (6): 1390-403. [ Links ]
25. Xiao L, Zhang L, Han W, Wang Z, Nattel S. Sex-based transmural differences in cardiac repolarization and ionic-current properties in canine left ventricles. Am J Physiol Heart Circ Physiol. 2006; 291 (2): H570-80. [ Links ]













