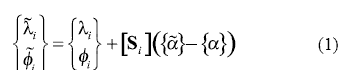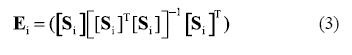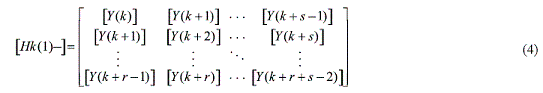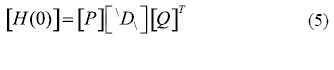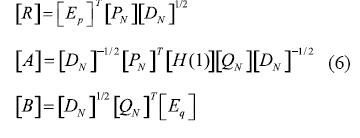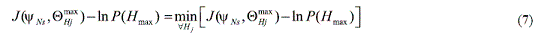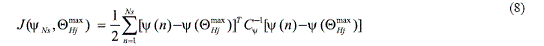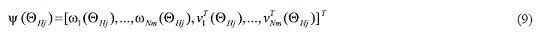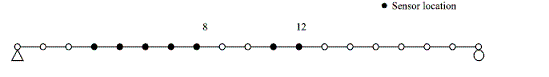Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230On-line version ISSN 2422-2844
Rev.fac.ing.univ. Antioquia no.39 Medellín Jan./Mar. 2007
Revista Facultad de Ingeniería N.o 39. pp. 42-55. Marzo, 2007
Abstract
Structural health monitoring of civil structures is currently receiving great amount of attention by researchers due to the economic impact and life-safety implications of early damage detection. Current visual inspection techniques, which aim to detect local damage, can be used in conjunction with a structural health monitoring system to inspect more localized regions. This paper presents a structural health monitoring methodology for simply supported bridges, which is divided into four steps; the first step deals with the optimum location of sensors using the concept of Fisher information matrix, the second and third steps use ambient excitation sources for system identification and the final step employs the Bayesian probabilistic approach to detect structural damage sites. A finite element model of a scaled bridge is used to carry out this numerical implementation. The results show that the proposed methodology can be implemented in the railway system of Medellín. The repetitive pattern of simply supported bridges can greatly facilitate the implementation of damage monitoring systems for the whole railway system.
---------- Key words: Eigenvector sensitivity method; natural excitation technique; eigensystem realization algorithm; the bayesian probabilistic approach for damage detection.
Metodología de monitoreo de daño estructural para puentes simplemente apoyados: implementación numérica
Resumen
El monitoreo de daño en estructuras civiles está recibiendo actualmente gran interés por parte de investigadores debido al gran impacto económico e implicaciones de seguridad relacionadas con una temprana detección de daño estructural. Las técnicas actuales de inspección visual, que en su gran mayoría han sido desarrolladas para detectar daño estructural a nivel local, pueden ser usadas junto con un sistema de monitoreo de daño estructural para inspeccionar zonas específicas de una estructura. En este artículo se presenta una metodología de monitoreo de daño estructural para puentes simplemente apoyados, esta metodología está dividida en cuatro niveles; el primer nivel plantea una óptima localización de sensores usando el concepto de la matriz de información Fisher; para el segundo y tercer nivel se plantea una identificación del sistema estructural con base en excitaciones ambientales y finalmente en el cuarto nivel se presenta un método probabilístico que utiliza el teorema de Bayes para detectar daño estructural. Un modelo en elementos finitos de un puente a escala es empleado para llevar a cabo esta implementación numérica. Los resultados muestran que la metodología propuesta en este artículo puede ser implementada en el sistema Metro de Medellín, pues este sistema está compuesto por una serie de puentes simplemente apoyados, lo cual facilitaría y justificaría la implementación de sistemas de monitoreo de daño para todo el sistema Metro de Medellín.
-----Palabras clave: método de sensitividad de modos de vibración, técnica de excitación natural, algoritmo de realización de valores propios, método de detección de daño estructural basado en el teorema de Bayes.
Introduction
Civil infrastructure including bridges and buildings forms a significant aspect of any nation's investment. Civil infrastructure systems play a vital role in the economic well-being of any country by producing enormous benefits under normal and healthy operation, on the other hand, their uncontrolled deterioration or malfunctioning can lead to huge economic loses and create a potential danger to civilians. Even in developed countries like the U.S. or Japan, the rapid deterioration of civil structures is overburden the budgets assigned to maintenance labors. In Japan, due to its rapid economic growth during the 1960’s and 1970’s resulted in construction of a considerable number of new civil structures to satisfy the economic demands; the construction boom during this period is, therefore, causing rapid and sudden aging of the Japanese civil infrastructure system at the beginning of this century.
An unhealthy civil structure is not reliable and demands more frequent inspection. In addition, during a major earthquake event, an unhealthy civil structure is prone to collapse. Current inspection techniques for civil structures are either visual or local experimental methods such as ultrasonic or acoustic methods, magnetic field methods, radiographs, eddy current methods and thermal field methods. The major drawbacks of these local experimental methods are that the location of damage must be known a priori and that there is a relatively high level of dependency on the practical skills of the engineers who carry out structural inspections. Visual inspection methods might not be the best solution for civil structures when the accessibility conditions represent potential danger to the inspectors or cause traffic disruption.
An innovative approach to asses the current health state of civil structures is the use of the dynamic properties of a structure to detect structural damage sites, the main idea behind this approach is that considerable changes in the modal properties such as natural frequencies, mode shapes and damping ratios provide quantitative information about the health condition of a structure. According to Rytter [1] a robust structural health monitoring (SHM) system can be divided into four levels: identification of damage that has occurred at a very early stage (Level I), localization of damage (Level II), quantification of damage (Level III) and prediction of the remaining useful life of the structure (Level IV). So far, many attempts have been made in order to implement SHM systems in real civil structures, but it is still challenging to achieve the four levels proposed by Rytter [1] in a real civil structure.
Today, the cost of installing structural monitoring systems for real applications is high. Lynch [2] pointed out that the cost of the Tsing Ma suspension bridge monitoring system was at a rate of US$27.000 per sensing channel, which is mainly due to the high installation and maintenance cost of system wires. The development of SHM systems has evolved into the consideration of sensing wireless technology, which is expected to reduce the cost of monitoring systems and make them more affordable for real applications. Modal identification and damage detection algorithms have been heavily studied at Los Alamos National Laboratory [3] using analytical and experimental data. A well-known test program is the set of damage tests inflicted on the I-40 plate girder bridge over the Rio Grande in Albuquerque in the U.S. [4], this program test is the most up-to-date, complete and valuable attempt to implement SHM systems in civil structures.
The SHM framework proposed in this paper consists of four steps; the first step is the optimum location of sensors for the purpose of damage detection, which is carried out using numerical models due to the fact that mass-normalized modes are needed; the second step extracts from ambient excitations sources free response behavior of a structure, which is used in the third step to obtain its modal information, and finally, by comparing the obtained modal parameters of the healthy and damaged structure, a probabilistic damage detection algorithm locates damaged sites and quantifies the level of structural damage. Optimum sensor location has been heavily studied over the past three decades. One of the most comprehensive studies was presented by Udwadia [5] named the Optimum Sensor Location Algorithm and is based on the Fisher information matrix. Kammer [6] presented the Effective Independence method, which selects sensor locations that contribute most to the linear independence of the mathematical mode shapes. The methods presented by Udwandia and Kammer improve modal identification results by finding optimum locations for sensors.
An alternative approach was presented by Hemez and Farhat [7] using the concept of the Fisher information matrix by placing sensors based on the strain energy contributions of a structure. This was the first method that considered the improvement in the damage detection results by optimally placing sensors. Shi et al. [8] presented a method in which the sensor configuration is selected based on its ability to localize structural damaged sites and is based on the method proposed by Hemez and Farhat [7]. Xia [9] extended the method proposed by Shi et al. [8] by considering the contribution of the measurement noise to find the optimum configuration of sensors.
Ambient sources of excitation, always present in civil structures, are wind and traffic loadings. Although a forced test can be conducted in order to extract modal information needed for damage detection, its use implies safety considerations when high values of excitation forces are needed and disruptions are caused by traffic interruption. In addition, it is almost impossible to completely eliminate sources of ambient excitations while performing a forced test. Therefore, ambient excitation sources are more suitable for the implementation of continuous monitoring systems.
Traffic loading on railway bridges has been studied at the University of Tokyo by Miyashita et al. [10] showing that cyclic external loads of the bogies generate forced vibration and the frequency is proportional to the train velocity. Traffic loading can be modeled under some assumptions as a stationary broadband force leading to the possibility to extract the free response of the structure, which can be used to extract its dynamic features.
Modal identification was firstly developed by aerospace engineers and then incorporated into the civil engineering field. There are many contributions to the development of system identification algorithms, which aim to identify natural frequencies, mode shapes and damping ratios from free response vibrations. One of the most widely used methods for modal identification is the Eigensystem Realization Algorithm (ERA) proposed by Juang and Papa [11]. This method has been successfully used during the last two decades for several researchers showing good performance in civil structures as reported by Caicedo et al. [12]. Several damage detection algorithms have been proposed during the last decade. Sohn et al. [13] presented a comprehensive report providing an up-to-date overview of existing damage detection methods. Damage detection methods can be mainly divided into two groups: deterministic and probabilistic methods. The most reliable up-to-date damage detection method was proposed by Sohn and Law [14]. Its best performance over existing damage detection methods was demonstrated by Sohn [15]. This method uses an error function, which allows multiple comparisons of damage configurations. Therefore, its probabilistic framework makes it more suitable for reliable implementation in real civil structures. Sohn [15] also studied the effect of temperature changes in modal extraction. In countries with wider seasonal temperature variations, temperature changes must be included in the implementation of continuous monitoring systems. The case presented in this paper deals with a monitoring system located in a tropical region where temperature variations through the year are expected not to have significant impact on the good performance of the monitoring system, and hence wont be considered herein. Another important fact, which is not included in this paper, is model updating as reported by Sohn [15].
This step will be considered when this proposal has evolved into the use of experimental data to update the finite element models.
The main objective of this paper is to present a SHM methodology for the simply supported bridges of the railway system of Medellín. A Finite element model of a scaled bridge will be used to show the implementation procedure, taking into consideration that it is impossible to develop a reliable monitoring system without using field measurements. Therefore, this study might be seen as a first attempt to implement such methodologies and must be complemented by analytical studies using the finite element models of the railway bridges and test programs conducted under controlled environments.
Problem formulation
Simply supported bridges are widely used all over the world as part of railway systems due to their construction advantages. The railway system of Medellín was opened to the public in 1995 with a total length of 28.8 km and 25 stations, a remarkable feature of the Medellín’s railway system is that 13 of the 25 stations are on a viaduct through the city center, the rest is at grade. Having 13 elevated stations connected to each other by simply supported bridges, the necessity for regular maintenance inspections after its first decade of usage is expected to gradually increase over the next years due to gradual deterioration of the bridge structures. Therefore, this paper presents a SHM methodology for real application to the railway system of Medellín. The repetitive pattern of the simply supported beams can greatly facilitate the implementation of damage monitoring systems for the whole railway system.
The proposed SHM methodology is divided into four steps: optimum sensor placement, impulse response synthesis from ambient measurements, system identification and structural damage detection. These steps are described in the following sections, and this discussion is followed by a description of the scaled bridge model used for this numerical implementation.
Optimum Sensor Placement
The optimum sensor placement method selected for this numerical implementation was proposed by Shi et al. [8], named Eigenvector Sensitivity method for convenience. The selection criteria of this method is based on analytical studies performed by Riveros-Jerez [16] where simply and continuous supported beams were subjected to optimum sensor placement analysis using the Eigenvector Sensitivity method [8], the Effective Independence method [6] and the Damage Measurability method [9]. Additional studies were also performed using sensors evenly distributed along the beams. A total number of 700 simulations using different conditions were carried out in order to study the performance of the aforementioned optimum sensor placement methods. The numerical results showed that the Eigenvector Sensitivity method performed the best for damage detection. Therefore, this method is selected to perform this numerical implementation.
The mathematical formulation of the Eigenvector Sensitivity method is based on the SB-EBE model updating method proposed by Hemez and Farhat [7] where the sensitivity matrix, Si, is used to correlate the measured vibration characteristics and the structural stiffness parameter {α}and {α}; before and after model updating, respectively, as shown in Eq. (1)
where λ φ and λ φ are the ith eigenfrequency and mode shape of the undamaged and damaged structure, respectively. Udwadia and Garba [17] demonstrated that maximizing the Fisher information matrix given in Eq. (2) would also maximize the covariance matrix leading to a best estimation of the difference between the structural stiffness parameters Δα = α (α)
The matrix, Bi, is the Fisher information matrix as a distribution of strain energy for the ith mode, and is derived from the Fisher information matrix which uses the mode shape matrix instead of the sensitivity matrix. The mode-shape based Fisher information matrix is used for the derivation of the Effective Independence method proposed by Kammer [6]. The Fisher information matrix as a distribution of strain energy, B, is then defined by the contribution of the selected modes. Kammer [6] also showed that the diagonal terms of the matrix, Ei, given in Eq. (3), could be used to rank the contribution of the selected mode shapes to a particular sensor configuration. Therefore, sensor locations with higher diagonal values in the matrix Ei must be selected as optimum locations. Further information about the calculation of the sensitivity matrix can be found in [9].
Impulse Response Synthesis from Ambient Measurements
On a continuous monitoring basis, only ambient excitation sources can be used to obtain impulse response function. The use of force test can be extremely useful for model updating. Farrar and James [18] found that if the unknown excitation is a white-noise random process, the cross-correlation function between two response measurements would have the same form as the free response of the structure. This method was named by the authors as the Natural Excitation Technique (NExT) and it is very important due to physical limitations to calculate the magnitude of the exciting forces during an ambient excitation test. This statement, therefore, allows us to use traffic loading to excite a simply supported bridge and obtain its free response. The mathematical derivation of this method and its experimental application can be found in [18].
System Identification
The use of accurate modal information for system identification will lead to reliable damage detection results. This fact is widely accepted in the research community. The most commonly used system identification methods are the extended Kalman Filters [19], the Polyreference time domain method [20], the Q-Markov COVER algorithm [21], and the Eigensystem Realization Algorithm (ERA) [11]. Caicedo [12] has shown the good performance of ERA for modal identification in civil structures highlighting its ability to handle measurement data corrupted by noise and indicators that allow quantification of the obtained modal parameters. Therefore, the proposed SHM methodology uses ERA for system identification.
Once, the free response of a structure is obtained by impulse response synthesis from ambient measurements, ERA is used to obtain its modal information. The mathematical formulation of ERA uses the Hankel matrix, which is formed using the response vector obtained from synthesi¬zed free-response. The generalized Hankel matrix consisting of Markov’s parameters is constructed as shown in Eq. (4)
where [Y(k)] is the Markov’s parameter obtained from structural impulse response at kth time step. The number of columns and rows are represented by r and s, respectively. The Hankel matrix is then evaluated for the [H(0)], and a singular value decomposition technique is performed as shown in Eq. (5).
The basic ERA’s theorem states that, if the dimension of any minimal realization is N, then the triplet shown in Eq. (6) is the minimum realization.
Where Ep, is defined as [[I] [0] ... [0]] and Eq is defined similarly. The unknown matrix A contains the eigenvalues and modal damping values of the structure and the matrix R is used for the transformation of the corrupted eigenvectors, in the state space matrix, to the physical state model. Further information about ERA’s derivation and its indicators can be found in [11].
Structural Damage Detection
The main objective of vibration-based damage detection methods is to evaluate the dynamic structural properties, such as stiffness, damping ratios and mode shapes, and monitor changes in their values related to structural damage. The type of damage, which is aimed to detect in this study, is structural damage that causes a stiffness decrease in the structure. It is still challenging the implementation of vibration-based damage detection techniques in real civil structures. There is still a debate whether measured deviations are significant enough to be a good damage detection indicator. In addition, it is widely known from sensitivity studies using finite element models and experimental data that local damage may not affect the global dynamic properties of the structure and considerable stiffness reduction may be needed in order to be detected [15].
Vibration-based damage detection methods can be mainly divided into deterministic and probabilistic methods. A deterministic approach might have the drawback that structural damage may not uniquely determined from the estimated modal data. Therefore, a probabilistic approach, where multiple damage scenarios can be analyzed, is more suitable for continuous monitoring systems. Sohn [15] using analytical and experimental data demonstrated the best performance of the Bayesian probabilistic approach for damage detection over deterministic vibration-based damage detection methods, such as the Damage Index method [22], which indeed showed the best performance during the vibration-based damage detection parametric studies using measurement data from artificial cuts in the I-40 bridge over the Rio Grande in New Mexico (Farrar and Jauregui [23]).
The mathematical formulation of the Bayesian probabilistic approach is based on an error function, defined by Sohn [15] in Eq. (7), and uses the Bayes theorem to find the largest posterior probability after observing a set of estimated modal parameters, each set of modal parameters consists of natural frequencies and mode shapes.
where ln is the natural logarithm function, Hmax, is the largest posterior probability that accounts for the hypothesis that contains the most likely damaged elements and the error function is defined in Eq. (8).
where and is a non-dimensional parameter which represents the contribution of the ith substructure stiffness to the system stiffness matrix. is the total collection of Ns data sets when multiple vibration sets are repeated, is a vector containing the variances estimated from the observation of the estimated modal parameter sets and the analytical modal set for a given is defined in Eq. (9).
The Bayesian probabilistic approach for damage detection offers three main advantages over other existing vibration-based damage detection methods: 1) multiple damage scenarios can be provided with their respective probabilities, 2) multiple measurement data sets can be included in the analysis leading to improvement of the accuracy of the damage detection results and, 3) system reliability/structural analysis or practical experience related to the occurrence of damage in a particular structure can be incorporated in the Bayesian framework as the prior probabilities of the damage events. The complete mathematical derivation of the Bayesian probabilistic approach for damage detection can be found in [15].
Description of the bridge and its finite element model
As previously mentioned, the main objective of this paper is to present the numerical implementation of a SHM methodology for the simply supported bridges of the railway system of Medellín. It is important to highlight that the static and dynamic properties of these bridges must be represented by the bridge selected for this numerical implementation. In order to accomplish this objective a scaled bridge used by Garibaldi et al. [24] is selected.
Garibaldi et al. [24] used ARMAV (Auto Regressive Moving Average Vector) models to analyze the dynamic behavior of a scaled bridge excited by traffic loading. The scaled bridge was designed according to the theory of scaled models, whose static and dynamic properties are compatible to real bridges as described by Garibaldi et al. [24]. They could identify successfully the modal properties of the scaled bridge under controlled experimental conditions and statistically defined traffic conditions. The scaled bridge was made of an aluminum beam, with a length of 1.86 m, a depth of 0.15 m, a thickness of 0.015 m, a Young’s modulus of 7 x 1010 N/m2, a density of 2700 kg/m3 and a total mass of 11.3 kg.
The experimental scaled bridge used by Garibaldi et al. [24] is used herein to numerically implement the proposed SHM methodology. The finite element model of the scaled bridge has 18 Euler-Bernoulli elements. Each element is 0.103 m length. The nodes at each end of the structure have fixed vertical DOFs and free rotational DOF. Only one supporting node has free horizontal DOF as shown in Figure 1. The mass and stiffness matrices assembled from the finite element model are used to obtain the Euler-Bernoulli natural frequencies, which are shown in table 1.
Table 1 System Identification Results
Numerical simulation
The simulation variables considered for this numerical implementation are based on the experimental values used by Garibaldi et al. [24]. The first step in the implementation of the proposed SHM methodology is the optimum location of sensors, which is performed using the Eigenvector Sensitivity method. It is important to note that this sensor placement study can only be performed using analytical models or experimental models where the exciting forces are known due to the fact that mass-normalized modes are needed. To locate sensors only vertical DOFs of the nodes will be used due to the vertical excitation nature of traffic loading.
The resulting sensor configuration using 8 vertical optimally located sensors is also shown in Figure 1, the number of sensors was kept the same as the number of sensors used by Garibaldi et al. [24] in their experimental scaled bridge. Further comparisons can be done to study the effectiveness in modal identification and damage detection of the sensor locations employed by Garibaldi et al. [24] and the sensor placement scheme presented herein.
Figure 1 Eight Sensor Configuration Using the Eigenvector Sensitivity Method
Once sensors are optimally located, indepen¬dent broad-band random noise excitations are generated for simulation of the stationary traffic loading excitation process, a maximum value of traffic load used for this simulation is 0.5 N, which is a value derived by Garibaldi et al. [24] to represent traffic loads in their experimental model using metallic spheres; where the masses and speeds of these spheres were linked to traffic loading on a real bridge. They assumed vehicles masses ranging from 700 to 1900 kg; as a result, considering a mass scale factor, the masses of the spheres were in the range of 0.016-0.043 kg.
Traffic loads are modeled as filtered Gaussian white noise (Gaussian white noise processes passed through a 6th order low-pass Butterworth filter with a 250 Hz cutoff). The stationary excitation forces are applied to all the 17 vertical DOFs of the bridge model simulating traffic loading excitation. A sampling frequency of 1 kHz and a sample length of 3 minutes are used to perform the simulation.
The acceleration records are only collected at the nodes where vertical sensors were optimally located. Once the acceleration records are collected, they are resample to 250 Hz due to the fact that the maximum analytical natural frequency is 90.10 Hz; this frequency corresponds to the third mode. To simulate the effect of measurement noise, a 10% RMS noise is added to the calculated acceleration records prior to the calculation of the free vibration records.
The second step of the SHM methodology accounts for the calculation of free vibration records from the traffic loading excitation process. The Natural Excitation technique is used to estimate impulse response functions from the accelerations records. NExT implementation has an advantage over the random decrement approach, which is also used to obtain free vibration records, that is the use of fast Fourier transform leading to a considerable shortage of its required computational time. The selection of the reference channel to perform the cross-correlation calculation is an important factor for the success of complete identification of the modes covered by the frequency range, if a node has no vertical motion within a mode shape and is selected as a reference channel, the mode shape where the node has no vertical motion will not be identified. The reference channel selected for the bridge model corresponds to node number 8 as shown in Figure 1.
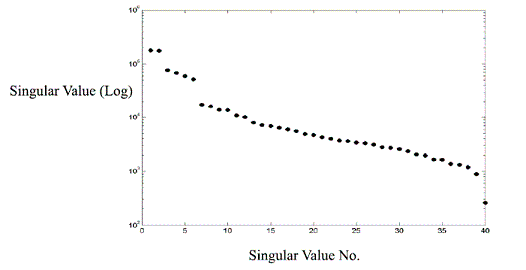
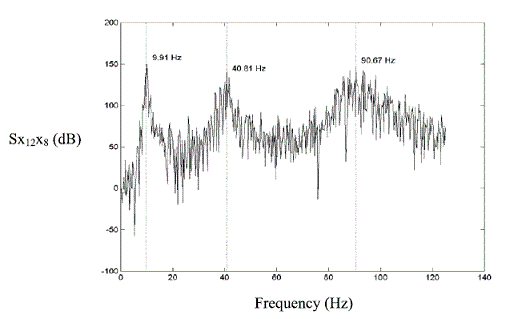
Free vibration records calculated from NExT are then used to perform system identification employing ERA. Only three modes can be identi¬fied considering the value of Nyquist frequency, which is the bandwidth of a sampled signal, and is equal to half the sampling frequency of that signal (125 Hz). A total number of 40 columns and 200 rows were used to compute the Hankel matrix. It can be seen from figure 2 that there is a considerable decay after the singular value number 6. Therefore, the Hankel matrix is reassembled using the first six singular values. Figure 3 shows the cross-spectral density function for node 12 using 1024 points per frame. A Hanning window was chosen to reduce the effects of leakage and 75% overlap was used for each frame [12].
Figure 2 Singular Values (Hankel Matrix)
Table 1 shows the natural frequencies obtained from the finite element model (Euler-Bernoulli), ARMAV models (Garibaldi et al. [25]) and the proposed system identification methodology (ERA) using 10% RMS measurement noise. It can be seen that ERA accurately identified the first three modes, even when measurement noise was added to the acceleration records showing its good performance as previously mentioned by Caicedo et al. [12].
Figure 3 Cross-Spectral Density Function for node 12 (Ref. Channel: 8)
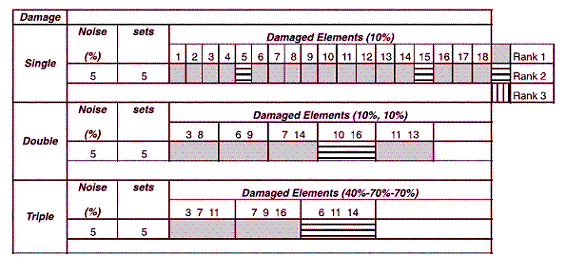
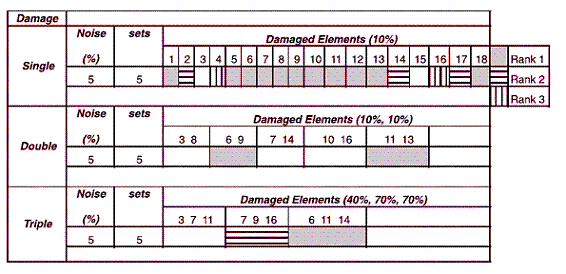
The final step in the numerical implementation of the proposed SHM methodology is structural damage detection. The Bayesian probabilistic approach for damage detection is numerically implemented by using the graphical user interface DAMTOOL developed at Stanford University by Lynch et al. [25]. Damage is defined as a determined stiffness reduction value of the selected element(s). A total number of 18 single damage scenarios, 5 double damage scenarios and 3 triple damage scenarios are studied. 5% RMS noise is added to the computed mode shapes and 5 measurements sets are considered for each damage case. Damage is successfully identified if the relative probability for the true damage case is located among the three highest probability values (Ranks).
A single damage scenario corresponds to an element whose stiffness is reduced in 10%; every element of the FEM is selected as a damage case. Table 2 shows the damage detection results for the single damage scenario, damage cases with stiffness reduction in elements 5 and 15 are identified with rank 2 on their error function values as previously defined in Eq. (7). A double damage scenario uses stiffness reduction of 10% of the selected elements. In table 2, only one double damage case ranks 2 on its error function value. Triple damage scenario corresponds to stiffness reduction in three elements at the same time, stiffness reductions of 40%, 40% and 70% are inflicted to the selected elements as shown in table 2, only one triple damage case ranks 2 on its error function value.
One of the characteristics of the Bayesian probabilistic approach is that the method yields a probabilistic ranking of the most probably damage scenarios based on the error function. The results may yield several cases with the same error due to the presence of random noise in the input information, but only one of these cases is correct. Therefore we only consider the damage case to be successfully identified if the correct damage is identified as one of the first three cases obtained with the same error function value. Rank 1 means that damage is correctly identified showing one
Table 2 Damage Detection Results (Sensors optimally located)
damage scenario with the lowest error value. Ranks 2 and 3 mean that two and three damage scenarios, respectively, have the same lowest error values. The results presented in table 2 show that most of the damage scenarios ranked 1, which is the highest confident level.
Finally, the damage detection results of an additional sensor configuration are presented in table 3. Eight sensors were evenly distributed along the length of the beam using the same damage scenarios. Blank cells mean that damage was not located. It can be seen from tables 2 and 3 that better detection results can be obtained if sensors are optimally located highlighting the importance of having an optimum sensor placement algorithm embedded into the SHM system.
Table 3 Damage Detection Results (Sensors evenly distributed)
Conclusion remarks
The numerical implementation of a SHM methodology for simple supported bridges was presented. A large-scale implementation on the elevated railway system of Medellín is envisioned over the next decade when the railway system reaches its second decade of usage. The main objective of this large-scale implementation is to reduce the cost of maintenance inspections by using a reliable SHM system.
Los Alamos National Laboratory LANL [13] has been leading structural health monitoring research for the last 10 years and one of its major achievements is DIAMOD (Damage Identification And MOdal aNalysis of Data) software that was developed as a package of modal analysis tools with some vibration-based damage detection algorithms included [26]. The Structural Health Monitoring (SHM) paradigm at LANL has now been redefined in the framework of statistical pattern recognition, which is expected to show better performance over existing damage detection algorithms and lead to the development of more powerful tools for damage detection [27]. The implementation of the statistical pattern recognition approach for damage detection, which is currently under development at LANL, must be explored in conjunction with the proposed SHM methodology for experimental implementations on the railway system of Medellín.
Another important issue to be considered for future implementations is the use of wireless monitoring systems for SMH systems as proposed by Lynch [2]. Therefore, high level research must be conducted in the area of sensing technology in order to accompany the experimental implementation on the railway system of Medellín. The sensor unit developed by Lynch [2], having embedded software, is one of the best available sensing technologies for SHM systems. It is expected that the cost of such sensing units will be gradually reduced make them more affordable for large-scale implementations. The proposed SHM methodology must also incorporate a model updating methodology for experimental implementations. Further research must be done in order to study existing model updating methodologies and find or develop a suitable model updating method to enhance the proposed SHM methodology.
The numerical implementation presented in this paper showed that it is possible to solve the problem of gradual deterioration of civil structures using the vibration-based approach, which indeed optimize the use of visual inspection and Non-Destructive Evaluation (NDE) techniques. The envisioned SHM approach for the railway system of Medellín must integrate global SHM and local NDE Techniques.
Acknowledgments
The author would like to greatly acknowledge Prof. Jerome Lynch (University of Michigan), Prof. Hoon Sohn (Carnegie-Mellon University) and Prof. Kincho Law (Stanford University) for providing DAMTOOL. The author would like to especially thank Professor Jerome Lynch for all the interesting and useful personal and technical discussions. The author would also like to acknowledge the considerable support and guidance given by Prof. Carlos Alberto Palacio Tobón (University of Antioquia) and Prof. Beatriz Amparo Wills Betancur (Universidad de Antioquia).
References
1. A. Rytter. Vibration Based Inspection of Civil Engineering Structures. Ph. D. dissertation. Department of Building Technology and Structural Engineering, Aalborg University, Denmark, 1993. pp. 193. [ Links ]
2. J. P. Lynch. Decentralization of Wireless Monitoring and Control Technologies for Civil Structures. Ph. D. dissertation, Department of Civil and Environmental Engineering, Stanford University, 2002. pp. 237. [ Links ]
3. S. W. Doebling, C. R. Farrar, M. B. Prime, D. W. Shevitz. “Damage Identification and Health Monitoring of Structural and Mechanical Systems from Changes in their Vibration Characteristics: A Literature Review”. Technical Report LA-13070-MS. Los Alamos National Laboratory, Los Alamos, NM. 1996. pp. 134. [ Links ]
4. C. R. Farrar, P. J. Cornwell, S. W. Doebling, M. B. Prime. “Structural Health Monitoring Studies of the Alamosa Canyon and I-40 Bridges”. Technical Report LA-13635-MS. Los Alamos National Laboratory, NM. 2000. pp. 141. [ Links ]
5. F. E. Udwadia. “Methodology for Optimum Sensor Locations for Parameter Identification in Dynamic Systems”. Journal of Engineering Mechanics. Vol. 102. 1994. pp. 368-390. [ Links ]
6. D. C. Kammer. “Sensor Placement for On-Orbit Modal Identification and Correlation of Large Space Structures”. Journal of Guidance, Control, and Dynamics. Vol. 14. 1991. pp. 251–259. [ Links ]
7. F. M. Hemez, C. Farhat. “An Energy Based Optimum Sensor Placement Criterion and Its Application to Structure Damage Detection”. Proc. 12th International Modal Analysis Conference (Honolulu, HI: Society of Experimental Mechanics). Vol. 19. 1994. pp. 1568–75. [ Links ]
8. Z. Y. Shi, S. S. Law, L. M. Zhang. “Optimum Sensor Placement for Structural Damage Detection”. Journal of Engineering Mechanics. Vol. 126. 2000. pp. 1173-1179. [ Links ]
9. Y. Xia. Condition Assessment of Structures Using Dynamic Data. Ph. D. dissertation. Nanyang Technological University, Singapore. 2002. pp. 210. [ Links ]
10. T. Miyashita, H. Ishii, Y. Fujino, A. Shoji, M. Seki. “Clarification of the Effect of High-Speed Train Induced Vibrations on a Railway Steel Box Girder Bridge Using Laser Doppler Vibrometer”. Proc. International Conference on Experimental Vibration Analysis for Civil Engineering Structures (Bordeaux, France). 2005. pp. 349-357. [ Links ]
11. J. N. Juang, R. S. Pappa. “An Eigensystem Realization Algorithm for Modal Parameter Identification and Model Reduction”. Journal of Guidance, Control, and Dynamics. Vol. 8. 1985. pp. 620-627. [ Links ]
12. J. M. Caicedo. Structural Health Monitoring of Flexible Structures. Ph. D. dissertation. Washington University in St. Louis, USA. 2003. pp. 172. [ Links ]
13. H. Sohn, C. R. Farrar, F. M. Hemez, D. D. Shunk, D. W. Stinemates, B. R. Nadler. “A Review of Structural Health Monitoring Literature: 1996-2001”. Technical Report LA-13976-MS. Los Alamos National Laboratory, Los Alamos, NM. 2003. pp. 307. [ Links ]
14. H. Sohn, K. Law. “Bayesian Probabilistic Approach for Structural Damage Detection”. Journal of Earthquake Engineering and Structural Dynamics. Vol. 26. 1997. pp. 1259-1281. [ Links ]
15. H. Sohn. A Bayesian Probabilistic Approach for Damage Detection for Civil Structures. Ph. D. dissertation. Department of Civil and Environmental Engineering, Stanford University, USA. 1998. pp. 220. [ Links ]
16. C.A. Riveros Jerez. Sensor Placement for Continuous Damage Monitoring on Cable-stayed Bridges: Numerical Implementation. Master thesis. Department of Civil Engineering, University of Tokyo, Japan. 2004. pp. 111. [ Links ]
17. F. E. Udwadia, J. A. Garba. “Optimal Sensor Locations for Structural Identification”, Proc. JPL Workgroup on Identification and Control of Flexible Space Structures (San Diego, CA). 1985. pp. 247-261. [ Links ]
18. C. R. Farrar, G. H. James III. “System identification from Ambient Vibration Measurement on a Bridge”. Journal of Sound and Vibration. Vol. 250. 1997. pp. 1-18. [ Links ]
19. M. Toshiba and E. Saito. “Structural Identification by Extended Kaman Filter”. Journal of Engineering Mechanics. ASCE. Vol. 110. 1984. pp. 1757-1770. [ Links ]
20. L. Zhang, H. Kanda, D. L. Brown, R. G. Allemang. “A Polyreference Frequency Domain Method for Modal Parameter Identification”. Technical Report ASME-85-DEC-106. American Society of Mechanical Engineering. 1985. pp. 6. [ Links ]
21. K. Lin, R. E. Skelton. “Q-Markov Covariance Equivalent Realization and its Application to Flexible Structure Identification”. Journal of Guidance, Control, and Dynamics. Vol. 16. 1993. pp. 308-319. [ Links ]
22. N. Stubbs, J. T. Kim, C. R. Farrar. “Field Verification of a Nondestructive Damage Localization and Severity Estimation Algorithm”. Proceedings 13th International Modal Analysis Conference, Nashville. TN. 1995. pp. 123-135. [ Links ]
23. C. R. Farrar, D. Jauregui. “Damage Detection Algorithms Applied to Experimental and Numerical Modal Data from the I-40 Bridge”. Technical Report LA-13074-MS. Los Alamos National Laboratory, Los Alamos, NM. 1996. pp. 135. [ Links ]
24. L. Garibaldi, E. Giorcelli, B. A. D. Piombo. “ARMAV Techniques for Traffic Excited Bridges”. ASME Journal of Vibrations and Acoustics. Vol. 120. 1998. pp. 713-718. [ Links ]
25. J. P. Lynch, H. Sohn, K. Law. “The Development and Application of a Damage Detection Toolbox for Matlab”. The 5th US National Congress on Computational Mechanics, University of Colorado at Boulder. CO. 1999. pp. 45-52. [ Links ]
26. S. W. Doebling, C.R. Farrar, P. J. Cornwell. “DIAMOND: A Graphical User Interface Toolbox for Comparative Modal Analysis and Damage Identification”. Proc. of the 6th International Conference on Recent Advances in Structural Dynamics, Southampton. UK. 1997. pp. 399-412. [ Links ]
27. D. W. Allen, J. A. Clough, H. Sohn, C. R. Farrar. “A Software Tool for Graphically Assembling Damage Identification Algorithms”. Smart Structures and Materials. Vol. 5057. 2003. pp. 138-144. [ Links ]
* Autor de correspondencia. Teléfono: +81+75-383-31 64, fax: +81+75-383-31 63, correo electrónico: riveros@udea.edu.co