Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Revista Facultad de Ingeniería Universidad de Antioquia
versão impressa ISSN 0120-6230versão On-line ISSN 2422-2844
Rev.fac.ing.univ. Antioquia n.43 Medellín jan./mar. 2008
Modelos de Gestión de Inventarios en Cadenas de Abastecimiento: Revisión de la Literatura
Inventory Management Models in Supply Chains: A Literature Review
Valentina Gutiérrez*, Carlos Julio Vidalb
a Universidad de Antioquia, Departamento de Ingeniería Industrial. A.A. 1226. Medellín, Colombia.
b Universidad del Valle, Escuela de Ingeniería Industrial y Estadística. Ciudad Universitaria Meléndez. Calle 13 No 100-00. Cali, Colombia.
Resumen
En este artículo se hace una revisión de los modelos de gestión para el diseño de políticas de inventarios de productos terminados y de materias primas en cadenas de abastecimiento, teniendo en cuenta la variabilidad de la demanda y los tiempos de suministro. El esquema de revisión se clasifica en cuatro secciones: (1) Modelos de Aleatoriedad de la Demanda, (2) Modelos de Aleatoriedad de los Tiempos de Suministro, (3) Modelos de Políticas de Inventarios, y (4) Modelos Integrados para la Gestión de Inventarios. Para cada sección se presentan tablas de resumen, describiendo las principales características de los modelos reportados. Se hace especial énfasis en la carencia de metodologías para modelar los aspectos variables del sistema y se identifican las oportunidades de investigación y desarrollo del área, en el contexto de la industria nacional.
Palabras clave: gestión de inventarios, aleatoriedad de la demanda, aleatoriedad de tiempos de suministro, políticas de inventarios, modelos de gestión.
Abstract
In this paper, we review inventory management models for designing inventory policies for final products and raw materials in supply chains, considering random demand and lead times. (1) Random Demand Models, (2) Random Lead Times Models, (3) Inventory Policy Models, and (4) Integrated Inventory Management Model. For each section we present summary tables describing the main characteristcs of models found in the literature. Special emphasis is placed on the lack of methodologies for modeling random issues of the system. Research and development opportunities in the context of the Colombian industry are also identified.
Keywords: inventory management, demand randomness, lead time randomness, inventory policies, management models.
Introducción
La gestión de un sistema de inventarios es una actividad transversal a la cadena de abastecimiento que constituye uno de los aspectos logísticos más complejos en cualquier sector de la economía. Las inversiones en los inventarios son cuantiosas y el control de capital asociado a las materias primas, los inventarios en proceso y los productos finales, constituyen una potencialidad para lograr mejoramientos en el sistema [1]. Sin embargo, esta complejidad en la gestión se hace cada vez más aguda teniendo en cuenta los efectos que generan fenómenos como la globalización, la apertura de mercados, el incremento en la diversificación de productos y referencias, la producción y distribución de productos con altos estándares de calidad, y la masificación de acceso a la información. Esto ha hecho que sea muy común escuchar a los administradores, gerentes y analistas de logística, que uno de los principales problemas que deben enfrentar es la administración de los inventarios. Como lo menciona Vidal [2], uno de los problemas típicos, es la existencia de excesos y faltantes: 'Siempre tenemos demasiado de lo que no se vende o se consume y muchos agotados de lo que sí se vende o se consume'. Este problema se conoce como desbalanceo de los inventarios.
Las decisiones típicas que deben tomarse al respecto de los inventarios han sido apoyadas por técnicas cuantitativas de la investigación de operaciones [3] y por el desarrollo de sistemas computacionales integrados denominados Enterprise Resource Planning (ERP) que aplican parte de los conceptos fundamentales de gestión, pero que presentan fallas en su implementación, especialmente en entornos culturales distintos a los entornos donde originalmente fueron creados [4].
En campos como la investigación de operaciones, buena parte de los esfuerzos que desde los años cincuenta han tenido lugar en áreas de la logística, se ha enfocado en la solución de los problemas complejos de la gestión de inventarios. Sin embargo, como lo menciona Wagner [5], a pesar del extenso trabajo en la investigación de modelos para gestionar los inventarios, las teorías desarrolladas son poco prácticas y actualmente no existe un panorama claro de cuáles son realmente las metodologías que deben utilizarse para mejorar la gestión de los inventarios mediante herramientas cuantitativas.
Este artículo presenta una revisión de los modelos de gestión para el diseño de políticas de inventarios de productos terminados y de materias primas en cadenas de abastecimiento, teniendo en cuenta la variabilidad de la demanda y de los tiempos de suministro. Estos dos aspectos inducen un grado de dificultad mayor a los modelos de gestión de inventarios y se puede afirmar que sus efectos han sido casi ignorados en la industria nacional, bien sea por desconocimiento o por limitaciones de recursos. En este contexto, se evidencia la necesidad de generar herramientas de apoyo para mejorar la gestión de dicho sistema, brindando soporte a las decisiones que deben tomarse en niveles tácticos y operativos del sistema, tales como:
- ¿Qué metodología debe implementarse para darle tratamiento de manera óptima a la aleatoriedad de la demanda de bienes finales y materias primas?
- ¿Cómo pueden modelarse los tiempos de suministro entre los nodos de una cadena de abastecimiento?
- ¿Cómo pueden estimarse de manera conjunta las políticas de inventarios de producto terminado y materias primas a lo largo de una cadena de abastecimiento?
En la sección dos se describe la literatura relevante asociada al problema, clasificada en cuatro categorías: los modelos para tratar la aleatoriedad de la demanda, los modelos para tratar la aleatoriedad de los tiempos de suministro, los modelos para definir políticas de inventarios de productos finales y materias primas, y los diferentes tipos de modelos para gestionar inventarios en cadenas de abastecimiento. En la sección tres se presentan las conclusiones y las oportunidades de investigación futuras.
Revisión de la Literatura
Modelos de Aleatoriedad de la Demanda
De acuerdo con Girlich y Chikán [6], el desarrollo conjunto de las teorías de inventarios y la aplicación de las matemáticas y la estadística se inició desde los años 50 cuando la Oficina de Investigación Naval de California destinaron recursos para la investigación en el área. Desde ese entonces, la diversidad de trabajos de investigación y extensión que se ha desarrollado es amplia, mediante la utilización de herramientas técnicas, clásicas y modernas. Puede admitirse que los modelos de aleatoriedad de la demanda independiente se clasifican en dos grupos: (1) los modelos clásicos y (2) las nuevas tendencias.
Dentro de la categoría de modelos clásicos, el método de tratamiento de la aleatoriedad de la demanda independiente más común, es ignorar dicho fenómeno en el diseño y operación de los sistemas de inventarios y de planeación de la producción. Asumir esta posición obedece a varias causas que varían dependiendo del contexto. En el ámbito de la investigación este fenómeno no se incluye porque en muchos casos incorporar tal comportamiento en el desarrollo de modelos, implica un grado de complejidad que hace que la modelación y los tiempos de solución computacionales se hagan prohibitivos. Por otro lado, en el ámbito industrial nacional, tal fenómeno real no se considera en los sistemas de diseño y control de inventarios y de producción, fundamentalmente por su desconocimiento y porque no se cuenta con herramientas cuantitativas que se adapten a la dinámica que siguen los sistemas productivos en el país.
Cuando se empieza a tener en cuenta la variabilidad de la demanda, una de las metodologías clásicas más comúnmente usada es la aplicación de sistemas de pronósticos. Entre los autores que han desarrollado con mayor detalle la aplicación de pronósticos a sistemas de inventarios se encuentran Vidal [2] y Silver et al. [7].
En la utilización de sistemas de pronósticos en modelos de gestión de inventarios, Snyder [8] ilustra que los sistemas tradicionales computacionales de control de inventarios confían en la suavización exponencial para pronosticar la demanda de ítems de alta rotación. El autor propone varias correcciones a éste método y aplica algunas modificaciones para contrarrestar ciertas dificultades comunes que se presentan en su implementación. Gallego y Toktay [9] consideran un proveedor que enfrenta demandas estacionarias y usa información de pronósticos dinámicamente actualizados para generar las órdenes a su distribuidor anterior en la cadena.
A nivel nacional, el trabajo desarrollado por Vidal et al. [10] aplica los sistemas de pronósticos a industrias locales. Los autores desarrollan una implementación doméstica mediante el uso de técnicas sencillas de pronósticos y de control de inventarios, mediante modelos de control de inventario periódico (R,S) para las compras en una bodega central y 34 detallistas en una cadena de abastecimiento de productos de consumo masivo.
Otra de las metodologías clásicas para tratar la aleatoriedad de la demanda, ha sido refinar modelos que en primera instancia asumen dicho fenómeno determinístico, pero que se hacen robustos incorporando la variabilidad de la demanda mediante distintas técnicas. La metodología más comúnmente utilizada es crear un esquema de tres escenarios: más probable, optimista y pesimista. Por ejemplo, Bulter [11] desarrolla un método mediante el esquema de escenarios para diseñar cadenas de abastecimiento para nuevos productos; en la modelación, se toma la demanda como una variable que induce incertidumbre, y se evalúan los tres escenarios variando los posibles valores que puede tomar la demanda. Otra forma es la desarrollada por Bertsimas y Thiele [12] quienes proponen una metodología general basada en optimización robusta para enfrentar el problema de control óptimo de cadenas de abastecimiento sujetas a demandas estocásticas en tiempos discretos. A pesar de que se toma en cuenta la incertidumbre de la demanda en la cadena, no se asume ninguna distribución específica.
Como parte de las nuevas tendencias para considerar la aleatoriedad de la demanda se reconocen dos grupos de metodologías: (1) la sistematización de los sistemas de pronósticos a través de la simulación y (2) la modelación estocástica. Parte de la sistematización de la aplicación de sistemas de pronósticos, ha sido la utilización de métodos de simulación que generalmente combinan series de tiempo con métodos causales, y la combinación simultánea de métodos cualitativos, de series de tiempo y causales. Packer [13] fue uno de los primeros autores en trabajar la simulación como técnica de sistematización de los pronósticos. El autor desarrolla un caso de estudio con el que demuestra que se pueden lograr mejoramientos significativos en los niveles promedio de inventario, el número de órdenes y el número de faltantes de inventario a través de la aplicación de técnicas sencillas de la investigación de operaciones.
Más recientemente, autores como Snyder et al. [14] han utilizado la simulación como técnica de mejoramiento de las metodologías de pronósticos mediante suavización exponencial. Los autores hacen una diferencia entre los ítems que tienen una alta rotación y los de baja rotación (caso que se presenta comúnmente en la mayoría de las industrias) y sistematizan el análisis de series de tiempo, a través del uso de herramientas de simulación como la Montecarlo para predecir los niveles de demanda y su relación con los Lead Times.
Otra de las formas de tratamiento de la aleatoriedad de la demanda es la modelación estocástica, la cual, a pesar de no ser muy conocida en el medio industrial nacional, ha sido utilizada como técnica desde la década de los veinte [6, 15]. Entre los trabajos más recientes, Chen [16] analiza un modelo de revisión periódico y horizonte infinito para un producto, en el cual se toman decisiones de fijación de precios y de producción e inventarios simultáneamente. En el trabajo de políticas de inventarios desarrollado por Gallego et al. [17] se modela la toma de decisiones de ordenamiento e inventarios de seguridad, asumiendo que la demanda sigue un proceso Poisson. Gudum y De Kok [18] desarrollan una técnica denominada Safety Stock Adjustment Procedure (SSAP), la cual permite determinar los inventarios de seguridad de modo que se cumplan los niveles de servicio, en estudios de simulación de sistemas de inventarios.
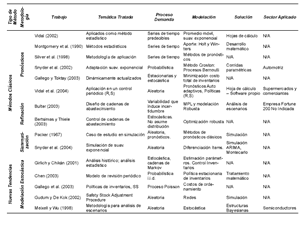
Otros autores que han trabajado en el tratamiento de la aleatoriedad de la demanda mediante modelación estocástica son Meixell y Wu [19], Hurter y Kaminsky [20], Treharne y Sox [21]. En la tabla 1 se presenta un resumen de los trabajos más relevantes en cada una de las categorías señaladas. De cada trabajo se reconoce la temática tratada, el proceso de modelación de la demanda, la solución si se brinda en el trabajo y el sector de aplicación. Para algunos trabajos, ciertas descripciones anteriores no aplican, o simplemente no se especifican en el trabajo.
Modelos de Aleatoriedad de los Tiempos de Reposición
A pesar de que en el medio industrial Colombiano apenas se está empezando a reconocer la variabilidad del tiempo que toma una orden desde se expide hasta que se recibe (tiempo conocido como tiempo de reposición o Lead Time - LT), es lógico pensar que dicho fenómeno sigue un comportamiento aleatorio. El tratamiento de la aleatoriedad de los LT no es un campo nuevo de estudio. Las cinco principales formas de tratar los tiempos de reposición para la toma de decisiones en sistemas de inventarios es asumir que los LT son: (1) nulos, es decir tasa de reposición infinita, (2) diferentes de cero y determinísticos, (3) diferentes de cero, aleatorios y son independientes e idénticamente distribuidos (i.i.d.), (4) diferentes de cero, aleatorios pero no i.i.d; (5) el último caso es analizar la demanda durante el LT a través de pronósticos y crear LT de seguridad.
Hay una última característica de los LT que es transversal a las cinco técnicas que se han mencionado y hace referencia al cruce de las órdenes en el tiempo, o 'Cross Orders'. En el contexto de las cadenas de abastecimiento reales, Riezbos [22] demuestra que no es válido suponer que las órdenes de productos y materias primas llegan en la misma secuencia en que fueron puestas, por lo que las políticas de control tradicionales deben ajustarse a dichas condiciones.
Tabla 1 Revisión de Modelos de Aleatoriedad de la Demanda - Haga un click para ampliar
Tradicionalmente, los LT se asumen fijos o como variables independientes e idénticamente distribuidas (i.i.d.) [23], que es el caso de las primeras tres técnicas de tratamiento presentadas. En lo que concierne a esta investigación, se tratan los LT como un fenómeno aleatorio, para lo cual resultan útiles las últimas tres técnicas citadas y no se consideran los trabajos que omiten la variabilidad de los LT.
Entre los autores que han incorporado los LT utilizando la técnica de modelación con variables aleatorias independientes, Kaplan [24], desarrolla un modelo dinámico de inventarios con LT estocásticos mediante un modelo de probabilidad que representa la llegada de órdenes pendientes, para lo cual, se asume que dichas órdenes no se cruzan en el tiempo y que las probabilidades de llegada son independientes del número y tamaño de la orden. Otros autores que trabajan esta metodología son Richards [25] y Sphicas [26]. Nevison y Burstein [27] tratan el problema de determinación dinámica de tamaños de lote con demandas determinísticas y LT estocásticos. Primero se asume que las distribuciones de los LT son arbitrarias e independientes del tamaño de lote, y no se admite cruce de órdenes en el tiempo, por lo que cada solución óptima cumplirá de manera exacta una secuencia de demandas consecutivas, lo cual es una extensión del resultado clásico de Wagner & Whitin [28]. Ehrhardt [29] estudia un modelo de inventarios con LT estocásticos bajo los supuestos de que los pedidos pendientes por llegar no se cruzan en el tiempo y que las distribuciones de los LT para una orden dada son independientes del número y tamaño de la orden. En el estudio se generan las condiciones para políticas de inventario óptimas en sistemas de control continuo (s, S) para horizontes finitos e infinitos.
En el contexto de cadenas de abastecimiento globales, Vidal y Goetschalckx [30] desarrollan un modelo matemático de programación entera mixta en el que se incorpora la aleatoriedad de los tiempos de reposición asociada a la selección de modos de transporte. Para incluir la incertidumbre que inducen los tiempos de reposición, los autores hacen uso del desarrollo de Silver et.al [7], quienes tratan los LT como variables aleatorias independientes.
Song y Yao [31] estudian un sistema en el que el producto final es ensamblado para despacho mientras que los componentes o sub-ensambles se fabrican contra inventario. Los autores asumen que la demanda sigue un proceso Poisson y que los tiempos de reposición para cada componente son variables aleatorias e idénticamente distribuidas (i.i.d.).
Eliminando el supuesto de que los LT se pueden representar como variables aleatorias i.i.d., se trabaja sobre la cuarta técnica de tratamiento mencionada. Suprimir este supuesto adquiere sentido por los trabajos desarrollados por autores citados por Gudum [23], quienes demuestran que dicho supuesto no es razonable y puede conducir a altos costos por penalidades y niveles de servicios muy bajos. Gudum ha hecho una exhaustiva revisión de las técnicas estadísticas y matemáticas para modelar los tiempos de reposición [32, 23, 18]. En el trabajo desarrollado en el 2002, Gudum propone una metodología para modelar la variabilidad en cadenas de abastecimiento desde la perspectiva del control de inventarios. En el 2003, la autora desarrolla dos trabajos para modelar la variabilidad de los LT's. En Gudum [23] se presenta una distribución alternativa de los LT, denominada distribución mixta de demoras atomizadas (mixed atom-delay distribution), la cual se basa en la idea de modelar los LT como una demora. En el trabajo, la autora crea una metodología para modelar la demanda durante los LT y la compara con las reglas tradicionales para tratar dicho fenómeno.
Finalmente, la técnica de análisis de la demanda durante los tiempos de reposición y la creación de LT de segunda [14] analizan la demanda durante los tiempos de reposición, creando LT de seguridad y proponen que la suavización exponencial se utiliza frecuentemente para pronosticar la demanda durante los tiempos de reposición (lead-time demand LTD). Los autores proveen una formulación para calcular las medias y las varianzas de las LTD para una amplia variedad de métodos de suavización exponencial. Kumar et al. [33] desarrollan un modelo de inventarios con demanda imprecisa, tiempos de reposición y costos de inventario para obtener una política que permita minimizar los costos.
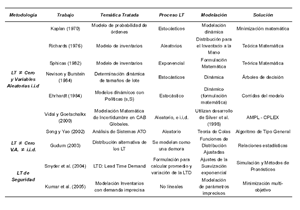
La tabla 2 presenta un resumen de los trabajos desarrollados en la modelación de los tiempos de suministro.
Modelos de Políticas de Inventarios
Una política de inventarios debe dar respuesta a las preguntas de cada cuánto debe revisarse el inventario, cuándo ordenar y cuánto ordenar, bien sea ítems de demanda independiente o dependiente. Sin embargo, la metodología de estimación de políticas para darle respuesta a estas preguntas puede variar significativamente debido a dos aspectos: (1) el tipo de producto (terminado o materia prima) y (2) el ambiente de producción.
En Gallego et al. [17] se hace un desarrollo matemático para abordar el problema de un minorista que se enfrenta con órdenes cuya demanda sigue un proceso Poisson, a un costo lineal con un tiempo fijo de reposición asociado L. Mediante el desarrollo, los autores logran demostrar que una política de nivel de inventario basada de orden en orden es óptima para este escenario. El aporte de este trabajo radica en el tratamiento matemático de la aleatoriedad de la demanda, y en el tratamiento de los LT que se consideran variables y fluctúan dependiendo del escenario de colocación de órdenes, para así generar una política de inventarios híbrida.
Bhatnagar et al. [34] se centran en la coordinación de la planeación de la producción cuando hay múltiples plantas en una empresa integrada verticalmente e identifican los aspectos que deben considerarse para determinar las decisiones de producción e inventarios para varias plantas, de modo que se logre un óptimo global. En este contexto, los autores clasifican la investigación de los aspectos a tener en cuenta en dicha coordinación en tres categorías: (1) planeación de producción y abastecimiento; (2) planeación de producción y distribución y (3) la planeación y distribución de los inventarios. Algunos autores citados por Bhatnagar et al. [34] estudian la problemática del nerviosismo en sistemas de planeación. La principal desventaja de estos trabajos es que se asume que los inventarios de seguridad son nulos, por lo que no se estudia la variabilidad de los tiempos de reposición de materias primas.
Lederman [35] explora el problema de la gestión de inventarios en el contexto de cadenas de abastecimiento, y se enfoca en la problemática de determinar políticas óptimas para componentes, cuando existe una superposición entre su demanda y la de los productos finales. El autor hace una exhaustiva evaluación de los métodos disponibles para determinar políticas de inventarios y de sus dificultades de implementación. El modelo se desarrolla a través de la simulación en un ambiente de producción de ensamble para órdenes (ATO, de su sigla en inglés Assemble to Order). Una de las principales debilidades del modelo desarrollado consiste en la suposición que los tiempos de reposición entre los nodos son nulos, y de hecho, entre las áreas futuras de investigación que el autor propone, se asume la correlación entre los LT y las decisiones que se toman en la ocurrencia de dichos periodos, así como la utilización de métodos heurísticos para la solución del problema, dada su particular complejidad.
En la estimación de políticas de inventarios en distintos ambientes de producción, el trabajo de Sarmiento y Nagi [36] describe los trabajos que se han desarrollado en el análisis integrado de sistemas de producción y distribución, cuestionando cómo los aspectos logísticos han influenciado el campo de trabajo y cuáles son las ventajas competitivas que se obtienen de la integración de las funciones de distribución con las funciones de producción en distintas empresas, en los niveles estratégico y táctico.
Crama et al. [37] generan una discusión alrededor de la literatura de metodologías de planeación de la producción con el objetivo de resaltar las diferencias y similitudes entre los aspectos y los modelos que surgen en distintos ambientes productivos y tener un mejor conocimiento de las situaciones que pueden presentarse en los sistemas de manufactura discreta. El aporte que los autores hacen para la determinación de políticas de inventarios, se centra en la discusión de las dificultades encontradas en la implementación de técnicas de control como los MRP y el JIT (Just in Time), enfocados especialmente en el concepto de 'receta', llevado a la práctica a través de la extensión del Bill of Materials (BOM) comúnmente utilizado en los sistemas de manufactura discreta.
Tabla 2 Revisión de Modelos de Aleatoriedad de Tiempos de Reposición - Lead Times - Haga un click para ampliar
Rosa [38] obtiene parámetros y políticas de control en la industria manufacturera del vidrio, en el cual se considera un sistema de produccióninventarios, multi-producto, multi-etapas de capacidad discreta en el tiempo, con ocurrencia de demanda aleatoria cada periodo. En el trabajo se analizan tres estrategias de producción: Make to Order (MTO), Make to Stock (MTS), Delayed Differenciation (DD de su sigla en inglés, que puede entenderse como principio de posposición de forma o más conocido como postponement). El autor utiliza datos del sector, y logra definir políticas de control de inventarios mediante simulación.
Pundoor [39] trabaja la simulación de cadenas de abastecimiento para evaluar el impacto de la reprogramación en la producción, en ambientes MTS y MTO y su efecto sobre la determinación de necesidades de materias primas y/o componentes. El autor justifica la simulación dada su flexibilidad para modelar fenómenos complejos típicos de los sistemas de suministro, y hace uso del software de simulación discreta ARENA. Teunter et al. [40] describen un sistema híbrido manufactura/remanufactura con un LT largo para manufactura y un LT corto para la remanufactura, y hacen una revisión bibliográfica de las estrategias de inventarios para sistemas híbridos cuando se asumen LT iguales. El principal aporte de este trabajo es el análisis sobre los LT de manufactura en sistemas de naturaleza push o pull, enfocado hacia una política de control de inventario de revisión continua (s, Q), en el sistema de manufactura.
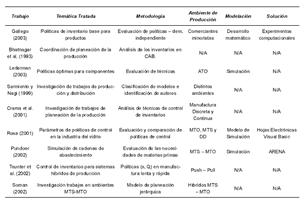
Soman et al. [41] hacen una revisión del estado del arte de los ambientes combinados MTS-MTO, enfocados hacia el sector de alimentos. Los autores proponen un sistema integral de planeación jerárquica para dar soporte a las decisiones en los ambientes productivos híbridos que hasta ahora se reconocen. En la tabla 3 se presenta un resumen de los trabajos citados esta sección, describiendo aquellos que hacen alusión al control de inventarios en distintos ambientes productivos.
Modelos Integrados de Gestión
En la estimación de inventarios de seguridad, Abhyankar y Graves [42] describen una aplicación a una empresa de la industria de semiconductores, en la que se implementa un inventario de seguridad para protegerse de la variabilidad de la demanda cíclica. Se construye un modelo sencillo de una cadena de abastecimiento de dos etapas y un modelo de optimización no lineal que permite determinar la localización óptima de inventarios de seguridad para minimizar el costo total de mantenimiento del inventario.
Graves et al. [43] aplican el trabajo a una multinacional norteamericana que fabrica herbicidas para maíz, soya y trigo, y para la cual se analiza la variabilidad de la demanda periodo a periodo, realizando comparaciones con los pronósticos y su grado de incertidumbre. Se evalúan múltiples escenarios de la demanda clasificándolos en los tres grupos típicos de escenarios: pesimista, más probable y optimista.
La temática de estimación de políticas óptimas y niveles de inventarios, ha sido trabajada por Shervais [44] quien enfrenta el problema de determinar un conjunto de políticas óptimas de inventarios y de transporte en un sistema de distribución multi-producto, multi-eslabón y multi-modal sujeto a demandas no estacionarias. El autor define que deben responderse las preguntas de dónde, cuándo y cómo en cuanto a: (1) la localización, es decir, cuánto de cada ítem debe mantener cada planta y cada depósito; (2) el ordenamiento, que se refiere a cuándo y cuánto ordenar de cada ítem y (3) el transporte, es decir, cómo deben despacharse los productos. En el diseño de la metodología, el autor desarrolla un algoritmo genético para encontrar la política base que permita iniciar cada siguiente etapa en la cadena.
Tabla 3 Revisión de Modelos para la Estimación de Políticas de Inventarios - Haga un click para ampliar
Katok et al. [45] desarrollan un sistema de soporte de decisiones para gestionar los inventarios de un proveedor mayorista de artículos de información para aviación. En el sistema se involucra la determinación del tamaño de órdenes de manuales de aviación, usados como herramientas de seguridad en los vuelos. Ketzember et al. [46] desarrollan un modelo heurístico para el problema común de producción e inventarios: múltiples productos, con demandas estacionarias y estocásticas, muchas ventas, y restricciones a lo largo de la producción, e intentan darle respuesta a tres preguntas comunes que surgen en estos ambientes: (1) cuándo empezar a producir más de las necesidades inmediatas en anticipación a las temporadas de alta demanda; (2) cómo programar la acumulación del inventario para los productos; (3) qué producir cuando las restricciones de la capacidad actual pueden resultar en faltantes inmediatos. Los autores concluyen que el uso de heurísticos es fundamental en el cálculo de políticas óptimas para los sistemas reales, pues argumentan que es imposible hacerlo de manera exacta.
La problemática de la gestión de los inventarios en cadenas de abastecimiento ha sido tratada por Van Mieghem y Rudi [47] quienes desarrollan una aplicación de redes derivada del problema tradicional del vendedor de periódicos (the newsvendor problem), denominada Newsvendor Network, en la que se admiten múltiples productos y múltiples procesos y puntos de almacenamiento para evaluar cómo las propiedades de un sistema de un solo periodo se extienden a una estructura dinámica.
Smits [48] desarrolla un diseño táctico de producción y distribución en cadenas de abastecimiento, teniendo en cuenta los inventarios de seguridad, las políticas de despacho y la planeación de la producción. En el trabajo se demuestra que en los modelos de nivel estratégico y táctico se asume comúnmente que los tiempos de reposición son variables exógenas, cuando en la realidad, ésta es una característica intrínseca de cada sistema y por lo tanto, se debe considerar como variable endógena.
Song y Chuin Lau [49] consideran un modelo de inventarios de revisión periódica y demanda estocástica, en el que se presenta obsolescencia repentina. En el trabajo se caracteriza la estructura de las políticas óptimas y se propone un algoritmo de programación dinámica para computar los parámetros. Liu et al. [50] buscan resolver los problemas de optimización que tienen restricciones no-lineales que capturan puntos clave de la dinámica de los sistemas complejos de producción e inventarios desarrollando un modelo de múltiples etapas de colas en los inventarios y el sistema de producción, con el objetivo de minimizar los costos de inventarios a lo largo de la cadena.
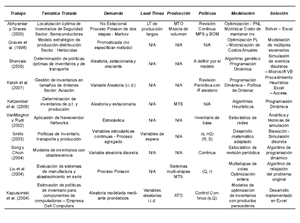
Finalmente, en el trabajo desarrollado por Kapuscinski et al. [51], se diseña un sistema de gestión para la toma de decisiones de los inventarios de la cadena de suministro de la empresa Dell Computers. Esta empresa, que no maneja inventarios de producto terminado, reconoce que debe enfocar sus esfuerzos al control de los componentes. Para ello se desarrolla un modelo de control de inventarios, el cual, mediante la aplicación de técnicas de pronósticos para la gestión de la demanda independiente y haciendo un análisis a los tiempos de reposición entre los nodos de la cadena, define los niveles de inventario de seguridad de los componentes. Igualmente, se crea una herramienta en Excel para la implementación de los métodos de control. La tabla 4 presenta un resumen de los trabajos revisados en esta sección.
Conclusiones
Para que las empresas mantengan su competitividad, es necesario definir una metodología que permita estimar las políticas de control de inventarios de productos terminados y materias primas a lo largo de su cadena de abastecimiento, considerando la naturaleza aleatoria de la demanda de productos terminados y de los tiempos de suministro entre las etapas de la cadena. A pesar de que actualmente existe un completo conjunto de modelos y métodos de solución para dar soporte a las decisiones del sistema de inventarios, no existe una metodología clara y unificada que brinde dicho soporte, particularmente en el contexto de cadenas regionales. Con base en la revisión bibliográfica se puede concluir que:
- De los métodos clásicos y las nuevas tendencias de modelación de la aleatoriedad de la demanda, han tenido una mayor aplicación práctica las metodologías de estimación mediante el análisis de series de tiempo, sistemas de pronósticos y refinamiento de los pronósticos haciendo uso la simulación y el desarrollo de herramientas computacionales para su automatización.
Tabla 4 Revisión de Modelos de Gestión de Inventarios - Haga un click para ampliar
- La implementación de modelos sencillos de pronósticos y técnicas de control de la demanda independiente en empresas Colombianas, han arrojado resultados de mejoramiento impresionantes, evidenciando la utilidad de los métodos y las oportunidades que existen en el medio industrial.
- La modelación de la aleatoriedad de fenómenos como la demanda y los tiempos de reposición ha sido trabajada exitosamente, con modelos estadísticos sencillos que asumen variables aleatorias independientes e idénticamente distribuidas, incluso en el diseño de cadenas de abastecimiento globales.
- Existe también un desarrollo estadístico significativo en la modelación del comportamiento de los tiempos de reposición entre los nodos de la cadena de abastecimiento, en el que se crean nuevas funciones de probabilidad para el fenómeno dependiendo del contexto de operación.
- No existe una metodología clara y unificada para definir el control de la demanda dependiente de manera integral con la demanda independiente. A pesar de que la modelación de la demanda independiente ha tenido un buen desarrollo, y que a su vez, la programación de los requerimientos de materiales en distintos ambientes productivos cuenta con una serie de técnicas para definir el control de la demanda dependiente, especialmente mediante métodos determinísticos, no hay un desarrollo que permita definir claramente cómo pasar de la demanda independiente a la demanda dependiente.
Algunos de los modelos revisados resuelven de manera práctica el problema de estimación de políticas de control, pero en ocasiones la separación de las problemáticas no permite lograr mejoramientos globales, sino que se centran en la búsqueda de óptimos en cada una de las ramas de estudio. Sin embargo, la optimización localizada en los módulos que conforman el sistema de inventarios, y la utilización conjunta de parámetros óptimos a lo largo de la cadena de una empresa, pueden generar mejoramientos significativos en la gestión de la industria nacional, especialmente en aquellas que no manejan ninguna herramienta de control.
Las oportunidades de investigación en las cuales los autores están trabajando actualmente, son:
- La identificación de las herramientas computacionales existentes en el uso de pronósticos de demanda y su evaluación para la aplicación en el medio industrial colombiano.
- La aplicación de las nuevas metodologías de modelación de la demanda como los procesos estocásticos y el refinamiento de herramientas computacionales existentes.
- La evaluación y comparación de las políticas de control básicas mediante indicadores como el costo total, el nivel de servicio y diversos indicadores logísticos y financieros que pueden ser fundamentales para la empresa, tales como la rotación del inventario, el porcentaje de inventario pagado y el retorno sobre la inversión en inventarios.
- La generación y evaluación de nuevas técnicas para crear metodologías que permitan determinar la mejor forma de relacionar la demanda independiente con la demanda dependiente en los diversos sectores de la industria.
- La formulación y solución de modelos más robustos que permitan darle solución al problema de investigación planteado, integrando la aleatoriedad de la demanda y los tiempos de reposición, la determinación de inventarios de seguridad, la localización de inventarios y la diversidad y complejidad que se alcanza cuando se consideran múltiples ítems de diversas características.
Referencias
1. S. Axsäter. Inventory Control. Kluwer Academic Publishers. Boston. 2000. pp. 2-5. [ Links ]
2. C. J. Vidal. Introducción a la gestión de inventarios. Universidad del Valle, Facultad de Ingeniería, Escuela de Ingeniería Industrial y Estadística. Cali. 2006. pp.1-16. [ Links ]
3. S. C. Graves, A. H. G. Rinnooy Kan, P. H. Zipkin. 'Handbooks in Operations Research and Management Science'. Logistics of Production and Inventory. Elsevier Science Publishers. North Holland. The Netherlands. Vol. 4. 1993. pp. 3-50. [ Links ]
4. X. Yajiong, H. Liang, W. R. Boulton, C. A. Snyder. 'ERP Implementation failures in China: Case studies with implication for ERP vendors'. International Journal of Production Economics. Vol. 97. 2005. pp. 279-295. [ Links ]
5. W. M. Harvey. 'And then there were none'. Operations Research. Vol. 50. 2002. pp. 217-226. [ Links ]
6. H. Girlich, A. Chikan. 'The Origins of Dynamic Inventory Modeling under Uncertainty: The men, their work and the connection with the Stanford Studies'. International Journal of Production Economics . Vol. 71. 2001. pp. 351-363. [ Links ]
7. E. A. Silver, D. F. Pyke, R. Peterson. Inventory Management and Production Planning and Scheduling. ed. 3. John Wiley & Sons, New York. 1998. pp. 74-130. [ Links ]
8. R. Snyder. 'Forecasting sales of slow and fast moving inventories'. European Journal of Operational Research. Vol. 140. 2002. pp. 684-699. [ Links ]
9. G. Gallego, L. B. Toktay. 'All-or-Nothing Ordering Under a Capacity Constrain and Forecast of Stationary Demand'. Research Paper. 2003. http://faculty.insead. edu/toktay/Articles/fcost newcut.pdf. Consultada agosto 14 de 2007. [ Links ]
10. C. J. Vidal, J. C. Londoño. F. Contreras. 'Aplicación de los Modelos de Inventarios en una Cadena de Abastecimiento de Productos de Consumo Masivo con una Bodega y N Puntos de Venta'. Ingeniería y Competitividad. Vol. 6. 2004. pp.35-52. [ Links ]
11. J. R. Bulter. Supply Chain Design for New Products. Doctoral Thesis. School of Industrial and Systems Engineering, Georgia Institute of Technology. USA. 2003. pp. 34-70. [ Links ]
12. B. Dimitris, A. Thiele. 'A Robust Optimization Approach to Supply Chain Management'. Research Paper. Massachusetts Institute of Technology. Cambridge, MA., 2003.http://web.mit.edu/dbertsim/ www/papers.html. consultado en agosto de 2007. [ Links ]
13. A. H. Packer. 'Simulation and adaptative forecasting as applied to inventory control' Operations Research. Vol. 15. 1967. pp. 660-679. [ Links ]
14. D. R. Snyder, A. B. Koehler, R. J. Hyndman, J. K. Ord. 'Exponential smoothing models: Means and variances for lead-time demand'. European Journal of Operational Research. Vol. 158. 2004. pp. 444-455. [ Links ]
15. A. Vazsonyi. 'The Use of Mathematics in Production and Inventory Control II' Management Science. Vol. 1. 1955. pp. 12-28. [ Links ]
16. D. C. Xin. 'Coordinating Inventory Control and Pricing Strategies with Randon Demand and Fixed Ordering Cost'. Manufacturing and Service Operations Management. Vol. 5. 2003. pp. 59-62. [ Links ]
17. G. Gallego, A. Muriel, T. Yildiz. 'Optimal Policies with Convertible Lead Times'. European Journal of Operational Research. Vol. 176. 2007. pp. 892-910. [ Links ]
18. K. C. Gudum, T. G. de Kok. 'A safety stock adjustment procedure to enable target service levels in simulation of generic inventory systems'. Research Paper. Department of Management Science and Statistics, Copenhagen Business School. Denmark. 2002. http://ir.lib.cbs.dk/download/ISBN/x656149131.pdf. Consultada en agosto 15 de 2007. [ Links ]
19. J. Meixell, S. D. Wu. 'Scenario Analysis in a Technology Market Using Leading Indicators'. IIE Transactions: Semicondor manufacturing. Vol. 14. 2001. pp. 66-75. [ Links ]
20. P. Hurter, F. Arthur, C. Kaminsky. 'An application of regenerative stochastic processes to a problem in inventory control'. Operations Research. Vol. 15. 1967. pp. 467-472. [ Links ]
21. T. J. Treharne, C. R. Sox. 'Adaptive Inventory Control for Nonstationary Demand and Partial Information'. Management Science. Vol. 48. 2002. pp. 607-624. [ Links ]
22. J. Riezbos. 'Inventory Order Crossovers'. International Journal of Production Economics. Vol. 102. 2006. pp. 666-675. [ Links ]
23. C. K. Gudum. 'A New Compound Lead Time Demand Distribution Approach and a Comparison Study'. Research Paper. Copenhagen Business School. Denmark. 2003. http://ir.lib.cbs.dk/download/ISBN/ x656193734.pdf. Consultada agosto 15 de 2007. [ Links ]
24. S. R. Kaplan. 'A Dynamic Inventory Model with Stochastic Lead Times'. Management Science. Vol. 16. 1970. pp. 491-507. [ Links ]
25. F. A. Russell Richards. 'Stochastic Model of a Repairable-Item Inventory System with Attrition and Random Lead Times'. Operations Research. Vol. 24. 1976. pp. 118-130. [ Links ]
26. P. Sphicas Georghios. 'On the Solution of an Inventory Model with Variable Lead Times'. Operations Research. Vol. 30. 1982. pp. 404-410. [ Links ]
27. C. Nevison, M. Burstein. 'The Dynamic Lot-Size Model with Stochastic Lead Times'. Management Science. Vol. 30. 1984. pp. 100-109. [ Links ]
28. H. Wagner. T. M. Whitin. 'Dynamic version of the economic lot size model'. Management Science, Vol. 50. 2004. pp. 1770-1774. [ Links ]
29. R. Ehrhardt. '(s, S) Policies for a Dynamic Inventory Model with Stochastic Lead Times'. Operations Research. Vol. 32. 1984. pp. 121-132. [ Links ]
30. C. J. Vidal. M. Goetschalckx. 'Modeling the Impact of Uncertainties on Global Logistics Systems'. Journal of Business Logistics. Vol. 21. 2000. pp. 95-120. [ Links ]
31. J. Song. D. D. Yao. 'Performance Analysis and Optimization of Assemble-To-Order Systems with Random Lead Times'. Operations Research. Vol. 50, No.5 (sept-oct. 2002); pp. 889-903. [ Links ]
32. C. K. Gudum. Managing variability in a supply chain: An inventory control perspective. Doctoral Thesis. Copenhagen Business School. Denmark. 2002. pp. 36-54. [ Links ]
33. J. D. Kumar, S. Kar, M. Maiti. 'An interactive method for inventory control with fuzzy lead-time and dynamic demand'. European Journal of Operational Research. Vol. 167. 2005. pp. 381- 397. [ Links ]
34. R. Bhatnagar, P. Chandra, S. K. Goyal. 'Models for multi-plant coordination'. European Journal of Operations Research. Vol. 67. 1993. pp. 141-160. [ Links ]
35. R. Lederman. Optimization of Stochastic Inventory Control with Correlated Demands. Undergraduate Thesis. Department of Computer Science. Brown University. USA 2003. pp. 3-19. [ Links ]
36. A. M. Sarmiento, R. Nagi. 'A review of integrated analysis of production-distribution systems'. IIE Transactions. Vol. 31. 1999. pp. 1061-1074. [ Links ]
37. Y. Crama, Y. Pochet, Y. Wera. 'A discussion of production planning approaches in the process industry'. Research Paper. 2001. http://citeseer.ist.psu.edu/cache/papers/crama01discussion.pdf. Consultada en agosto 15 de 2007. [ Links ]
38. M. N. Rosa. Make-to-Stock vs. Make-to-Order in Glass Manufacturing. Master Thesis. Universidad Técnica de Lisboa. Instituto Superior Técnico. Lisboa, Portugal, 2001. pp. 29-52. [ Links ]
39. G. Pundoor. Supply Chain Simulation Models for Evaluating the Impact of Rescheduling Frequencies. Master Thesis. Institute for Systems Research. University of Maryland, 2002. pp. 23-41. [ Links ]
40. R. Teunter. E. van der Laan, D. Vlachos. 'Inventory strategies for systems with fast remanufacturing'. Journal of the Operational Research Society. Vol. 55. 2004. pp.475-484. [ Links ]
41. C. A. Soman. D. Pieter van Donk, G. Gaalman. Combined make-to-order make-to-stock in a food production system. International Journal of Production Economics. Vol. 90. 2004. pp. 223-235. [ Links ]
42. H. S. Abhyankar. S. Graves. 'Creating an Inventory Hedge for Markov Modulated Poisson Demand: An Application and Model'. Manufacturing and Service Operations Management. Vol. 3. 2001. pp. 306-320. [ Links ]
43. S. C. Graves, C. Gutiérrez, M. J. Pulwer, H. S. Sidhu. G. L. Weihs. 'Optimizing Monsanto's Supply Chain under Uncertain Demand'. Research Paper. MIT. Cambridge, MA. 1998. http://web.mit.edu/graves/www/papers/ monsanto.pdf. Consultada en agosto 15 de 2007. [ Links ]
44. S. Shervais. Adaptive critic design of control policies for multi-echelon inventory systems. Doctoral Thesis. Portland State University. USA, 2000. pp. 59-96. [ Links ]
45. E. Katok, A. Lathrop, W. Tarantino, S. H. Xu. 'Jeppesen Uses a Dynamic Programming-Based DSS to Manage Inventory'. Interfaces. Vol. 31. 2001. pp. 54-65. [ Links ]
46. M. Ketzember, R. Metters, J. Semple. 'A Heuristic for Multi-Item Production with Seasonal Demand'. IIE Transactions. Vol. 38. 2006. pp.201-211. [ Links ]
47. J. A. Van Mieghem, N. Rudi. 'Newsvendor Networks: Inventory Management and Capacity Investment with Discretionary Activities'. Manufacturing and Service Operations Management. Vol. 4. 2002. pp. 313-335. [ Links ]
48. S. Smits. Tactical design of production distribution networks: safety stock, shipment, and production planning. Doctoral Thesis. Technische Universiteit Eindhoven. 2003. pp.109-152. [ Links ]
49. Y. Song, H. Chuin Lau. 'A periodic review inventory model with application to continuousreview obsolescence problem'. European Journal of Operational Research. Vol. 159. 2004. pp. 110-120. [ Links ]
50. L. Liu, L. Xiaoming, D. D. Yao. 'Analysis and Optimization of a Multistage Inventory-Queue System'. Management Science. Vol. 50. 2004. pp. 365-380. [ Links ]
51. R. Kapuscinski, R. Q. Zhang, P. Carbonneau, R. Moore, Bill Reeves. 'Inventory Decisions in Dell's Supply Chain'. Interfaces. Vol. 34. 2004. pp. 191-205. [ Links ]
(Recibido el 25 de enero de 2007. Aceptado 8 de noviembre de 2007)
* Autor de correspondencia: teléfono: + 57 + 4 + 219 55 75, fax: + 57 + 4 + 263 82 82, correo electrónico: evlaila@udea.edu.co (V. Gutiérrez).