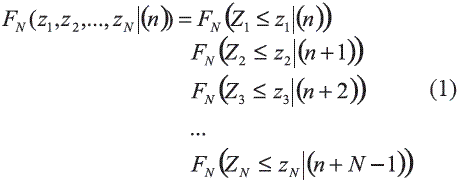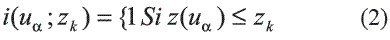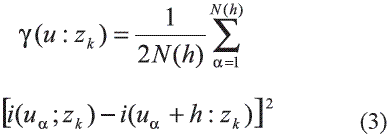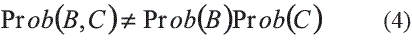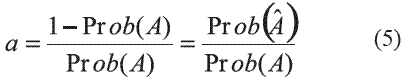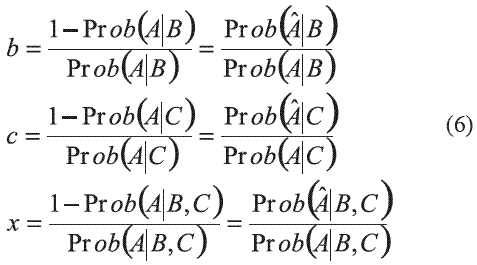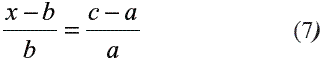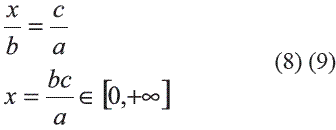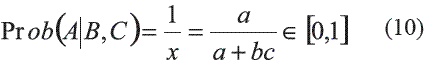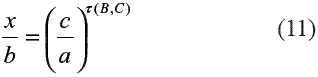Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230On-line version ISSN 2422-2844
Rev.fac.ing.univ. Antioquia no.50 Medellín Oct./Dec. 2009
Análisis de metodologías geoestadísticas alternativas en la modelación del acuífero Morroa (Sucre-Colombia)
Alternative geostatistics tools applied to Morroa aquifer modeling (Sucre-Colombia)
Aníbal Pérez García1*, Nelson Obregón Neira2, Oscar García Cabrejo3
1Facultad de Ingeniería Ambiental, Universidad Antonio Nariño, Cra. 3E No 47-15 B4 P4. Bogotá, Colombia
2Grupo "Hidrociencias", Universidad Javeriana, Carrera 7 No 40-62- Edificio Central 6o Piso. Bogotá, Colombia
3Departamento de Ingeniería Civil, Universidad Javeriana. Carrera 7 No 40-62 -Edificio Central 6.o Piso. Bogotá, Colombia
Resumen
En este trabajo se llevan a cabo una serie de simulaciones estocásticas y algunos principios derivados de la Geoestadística de Puntos Múltiples (MPS) usando una metodología comparativa compuesta por dos fases. En la primera, se desarrolla una técnica basada en el concepto de semivariograma llamada Simulación Estocástica Condicional (SEC) y más específicamente la Simulación Secuencial Indicador (SISIM), aplicándola en el marco de la modelación del Acuífero Morroa (Sucre-Colombia). En la segunda, se logra implementar un moderno algoritmo denominado SNESIM [1] complementado por el Modelo Tau (ξ), con el fin de incorporar todo tipo de información disponible para la definición de las facie del Acuífero. Las simulaciones son realizadas a través del uso de algoritmos construidos por [1,2] y el software S-Gems desarrollado por la Universidad de Stanford [3]. Los resultados muestran la conveniencia de emplear imágenes de entrenamiento y el modelo ξ para la integración de información geosísmica y de pozos, así como también la Simulación Estocástica en la configuración de modelos hidrogeológicos, especialmente cuando la información disponible es insuficiente y difusa.
Palabras clave: Acuífero Morroa, modelación de aguas subterráneas, geoestadística, simulación estocástica condicional, geoestadística de puntos múltiples, datos duros, datos suaves.
Abstract
In this paper, stochastic simulations and some multiple-point geostatistical principles are developed using a comparative methodology consisting of two phases. First, a traditional methodology based on variogram concepts called Conditional Stochastic Simulation (CSS) and more specifically the Sequential Indicator Simulation (SISIM) is applied to the aquifer modeling. Secondly, modern algorithm based on multiple-point geostatistics called SNESIM [1] and ξ Model [4] are implemented to integrate information available in the definition of Morroa aquifer facies. The simulations are realized by using algorithms constructed in references [1, 2] and S-Gems software prepared at Stanford University[3]. Results show the convenience of employing training images with soft and hard data conditioning integrated by ξ Model, and CSS for configuring hydrogeological models when barely deficient information is available.
Keywords: Morroa Aquifer, groundwater modeling, geostatistics, conditional stochastic simulation, multiple-point statistics, soft data, hard data.
Introducción
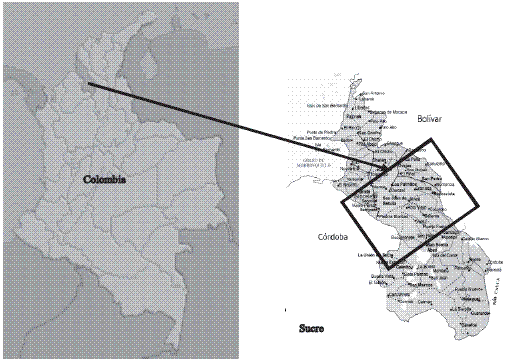
En Colombia, la información hidrológica disponible no es suficiente para definir escenarios de escasez de agua, esta situación es particularmente grave en zonas donde los acuíferos constituyen la única fuente de suministro de agua. Una de estas zonas es el acuífero Morroa, el cual posee una gran extensión (según aproximaciones previas alrededor de 9000 km2) asociada a los departamentos de Sucre, Bolívar y Córdoba en la costa norte colombiana. Esta fuente subsuperficial suministra el agua potable de una gran población (alrededor de 400.000 personas) que habita en muchas ciudades ubicadas principalmente en el departamento de Sucre. Desde hace muchos años, estas poblaciones han venido sufriendo muchos problemas relacionados con el suministro del líquido, por esta razón, éste se ha convertido en un problema de interés nacional. En la zona de estudio (Figura 1) se han desarrollado numerosos proyectos que planeaban reconstruir las estructuras hidroestratigráficas del acuífero, capturando la heterogeneidad y reproduciendo la totalidad de la compleja información litológica relacionada con el Acuífero y sus respectivas características hidrogeológicas. A partir de una recopilación de información secundaria se desarrolló un modelo de flujo del acuífero Morroa que incluye datos relacionados con cortes geológicos, interpretaciones geológicas y valores globales de parámetros hidráulicos [5], sin embargo su área de estudio se limitó sólo a la zona de recarga del acuífero, ya que no se contaba con información de la distribución de las unidades hidroestartográficas en la totalidad del acuífero. A partir de la aplicación de diferentes métodos relacionados en la literatura para la estimación de parámetros hidrógeológicos, se realizó una investigación de campo para determinar conductividades hidráulicas en varias zonas del acuífero [6]. Desafortunadamente su estudio se limitó a la determinación de parámetros hidráulicos. Recientemente, sellevó a cabo una interpretación de líneas sísmicas implementadas en la zona [7], dichas interpretaciones definieron de manera general la extensión del acuífero y sus límites, una conclusión importante de esta investigación es que descartó la conexión hidráulica entre el acuífero Morroa y la región de la Mojana, la cual se habia asumido por muchos años. Esta es la única aproximación que logra estudiar, de manera global la totalidad del acuífero y da muchas luces del comportamiento hidroestratigráfico de la formación. Sin embargo, las limitaciones del uso de sólo métodos geofísicos en la determinación de unidades hidrogeológicas han sido ampliamente discutidas [8,9,10]. En resumen, aunque se han obtenido resultados coincidentes en lo que tiene que ver con la estructura geológica, ha sido imposible determinar la hetereogeneidad del acuífero Morroa a partir de métodos convencionales. Por tanto, es indispensable implementar nuevas herramientas en la determinación del modelo conceptual del acuífero.
Figura 1 Localización del Acuífero Morroa
A pesar de los esfuerzos realizados por las instituciones colombianas, este problema no ha sido resuelto, principalmente porque no hay información que permita construir un modelo conceptual confiable a través del uso de metodologías tradicionales. Además, se debe tener en cuenta que esta área es muy compleja desde el punto de vista estratigráfico, lo que ha imposibilitado la definición total de las estructuras geológicas, en especial las presentes en el centro y el oriente del cuerpo de agua (edades geológicas y espesores de las formaciones no están claros). Adicionalmente, debido a que existe sólo un pequeño número de pozos situados hasta profundidades de 500 m, no hay suficientes datos que definan el comportamiento del Acuífero. Por otra parte, recientemente se ha llevado a cabo un análisis sísmico del área de estudio [7] capaz de describir en una mejor forma algunas características del mismo, sin embargo, esta información sólo puede ser considerada como información blanda.
Por otra parte, algunas investigaciones previas [11,12,4] han usado metodologías basadas en estructuras globales, descritas geoestadísticamente por el semivariograma, en la modelación de problemas en geociencias. Los principales algoritmos basados en este concepto son la Simulación Secuencial Gaussiana (SGSIM) [13] y la Simulación Secuencial Indicador(SISIM) [4]. Aunque SGSIM es muy popular dentro de los modeladores, es sabido que tiene muchas limitaciones [14,13,1], dentro de las cuales la más crítica está ligada a la propiedad de máxima entropía de cualquier modelo Gaussiano multivariado, que establece que el modelo Gaussiano es el menos estructurado dentro de todos los modelos compartiendo la misma covarianza (Variograma) [15], entonces, a pesar de ser globalmente más preciso que el krigeado, SGSIM aún falla en la determinación de patrones específicos de modelación de la conectividad geológica estructurada. Por otra parte, SISIM permite el uso de diferentes variogramas indicadores para modelar las relaciones de cada uno de los intervalos [15].
Debido a las grandes limitaciones de la estadística tradicional para simular heterogeneidades curvilíneas complejas, por estar basada en estadística de dos puntos (variograma), se han propuesto algunas tecnologías que capturan estadística de puntos múltiples a partir del uso de imágenes de entrenamiento simulándolas dentro de la subsuperficie e integrándola y condicionándola con datos duros y datos blandos.
Este trabajo, se presenta una nueva metodología fundamentada en la integración de la información mediante la construcción de algoritmos basados en estructuras orientadas a objetos. Por tanto, se intenta con este esfuerzo: (1) introducir una metodología en donde la información difusa pueda ser usada para crear modelos conceptuales complejos basados en teorías geoestadísticas modernas y simulaciones condicionales, (2) definir la variabilidad hidroestratigráfica asociada a un modelo conceptual del Acuífero Morroa que abarque su total extensión y (3) encontrar algunas estrategias que contribuyan en la solución de los problemas de abastecimiento en el Departamento de Sucre (Colombia).
Metodología
La modelación de aguas subterráneas está soportada en la definición de las propiedades hidráulicas de la zona subsuperficial, sin embargo, existen un sinnúmero de limitaciones físicas y económicas que impiden representar de una forma determinista estas propiedades. Consecuentemente, en las últimas décadas se han encontrado numerosas respuestas estocásticas a esta problemática. Estos métodos permiten integrar datos medidos en campo con información geofísica e hidrogeológica con el fin de construir una simulación de la formación geológica estudiada. Existen muchas metodologías que llevan a cabo modelos muy eficientes que incorporan la totalidad de la información disponible, usualmente relacionadas a interpretaciones geológicas, pozos y características sísmicas, entre otras.
Simulación estocástica condicional (SEC)
Se pretende implementar una metodología tradicional, basada en el uso de variogramas, denominada Simulación Estocástica Condicional (SEC), la cual representa una aproximación más refinada que el arraigado método de Krigueado ([16,17]), ya que permite corregir los errores derivados de la suavización relacionados con la sobre y subestimación de los valores y con la incapacidad para reproducir la variabilidad espacial de las estructuras.
El objetivo de la SEC es la reproducción de los rasgos globales como la "textura" (definida aquí como la apariencia física de las formaciones geológicas, asociada usualmente a grandes extensiones), y características estadísticas como el histograma y el variograma/covarianza. Adicionalmente, esta metodología permite obtener valores de incertidumbre por medio de las diferencias entre valores simulados, ya sea en una ubicación específica (exactitud local) o en campos aleatorios simulados (exactitud global o conjunta), solucionando así el problema de exactitud del krigeado en zonas de poca densidad de información. La metodología más usada de la Simulación Estocástica Condicional es la Simulación Secuencial.
Consideremos la distribución conjunta de N variables aleatorias Zi, donde N puede ser un valor grande. Las N variables aleatorias Zi pueden representar el mismo atributo en N nodos de una malla que discretiza el área de estudio A. El procedimiento de condicionamiento de estas N variables aleatorias por conjuntos de datos n de cualquier tipo (continuos o categóricos (valores discretos clasificados en categorías)), lo cual se representa mediante la notación |(n). La correspondiente distribución acumulada condicional se puede denotar como:
Este procedimiento es completamente general e independiente del algoritmo o método empleado para la determinación de la secuencia de distribuciones univariadas. Dependiendo de la forma que asuman las distribuciones locales, aparecen los algoritmos de Simulación Secuencial Gaussiana (las distribuciones son normales), Indicador (las distribuciones son no-paramétricas) o directa (de cualquier forma pero sin transformación de datos).
Aquí, se usa el algoritmo de Simulación Secuencial Indicador (llamado SISIM por la sigla en inglés) el cual se describe a continuación:
1. Discretizar el rango de variación de z(variable a ser calculada) en (k + 1) clases usando k valores zk. Posteriormente transformar cada dato z (ua); donde ua representa el nodo (ubicación) donde la variable está siendo calculada; en un vector de indicadores definidos:
2. Calcular y modelar los semivariogramas indicadores de las k clases:
3. Definir una ruta aleatoria que visite todos los nodos a simular.
4. En cada nodo ua:
a. Determinar las k probabilidades acumuladas usando krigeado indicador. La información condicionante (n) consiste en indicadores de los datos originales y los datos previamente simulados.
b. Corregir cualquier violación de las relaciones de orden y posteriormente construir la distribución acumulada condicional F(u';z|(n)) usando algoritmos de interpolación extrapolación, donde u' expresa el nodo simulado.
c. Obtener un valor simulado a partir de la distribución definida anteriormente por el método de inversión.
d. Agregar el valor simulado al conjunto de datos condicionantes.
e. Continuar al siguiente nodo de la ruta aleatoria definida y repetir los pasos del 1 al 4.
Entonces, se pueden construir diferentes realizaciones utilizando rutas aleatorias diversas. Las simulaciones geoestadísticas tratan de producir una serie de imágenes, o realizaciones que representen un rango de posibilidades. Esto nos permite tener muchas imágenes reproduciendo el histograma y el variograma de los datos de entrada. Se debe tener en cuenta aquí que una realización es una aproximación mucho menos precisa que el krigeado, sin embargo el promedio de una selección de realizaciones puede servir para construir un buen estimativo.
Por otra parte, una de las más modernas técnicas usadas actualmente es la geoestadística de puntos múltiples, la cual tiene en cuenta correlaciones entre más de dos puntos siendo capaz de reproducir estructuras geológicas más complejas. Las tareas relacionadas con la integración y el condicionamiento de datos blandos y datos duros es hecha a través del Modelo ξ [4, 18].
Geostadística de puntos múltiples (MPS)
La necesidad de ir más allá de los variogramas requiere la búsqueda constante de métodos que usen Geoestadística de Puntos Múltiples. Este concepto está basado en el uso de imágenes de entrenamiento en lugar de datos con localización específica como krigeado y SEC. Estas imágenes proveen las relaciones requeridas por la MPS, y aunque no necesitan estar condicionadas a ninguna información subsuperficial especifíca deben representar un concepto geológico a priori.
Las imágenes de entrenamiento pueden provenir de diferentes fuentes tales como gráficos geológicos y fotografías de afloramientos interpretadas debidamente digitalizadas y extendidas a imágenes 3D (normalmente usando programas CAD), así mismo realizaciones de un algoritmo basado en objetos. Otra alternativa sería usar muchas imágenes de entrenamiento, cada una de ellas reflejando diferentes tipos de heteregeoneidad en diferentes escalas [12].
Existen muchas metodologías que usan conceptos relacionados con MPS, dentro de ellas podemos resaltar: 1) una propuesta usando recocido simulado (simulated annealing) propuesta por [19, 20]. 2), un campo aleatorio de Markov propuesto por [21], 3), un método basado en Redes Neuronales Artificiales propuesto [22] y finalmente 4) una simulación secuencial extendida, basada en la inferencia de la probabilidad condicional a través del escaneo de la imagen de entrenamiento y la reproducción de los eventos allí encontrados.
A pesar de que esta última propuesta requiere grandes gastos computacionales debido a la necesidad de escanear la imagen de entrenamiento en cada punto del camino aleatorio, [1] propone para superar este inconveniente, usar una estructura de datos espaciales. Este algoritmo desarrollado por Strabelle está fundamentado en el paradigma de la simulación secuencial por medio de la cual cada valor simulado se convierte en un dato que condiciona la simulación de los valores vecinos [23].
El algoritmo es llamado SNESIM para insistir en el hecho que sólo utiliza una ecuación simple normal para modelar la probabilidad de ocurrencia de una facie en un nodo particular de la malla. Esta ecuación es la reconocida relación de Bayes que define una probabilidad condicional. Por esta razón, el método elimina la necesidad de resolver un sistema completo de krigeado en cada nodo no informado; en lugar de esto, deriva la probabilidad directamente a partir de una ecuación simple equivalente a la identificación de una proporción leída de la imagen de entrenamiento.
SNESIM escanea la imagen de entrenamiento usando una plantilla predeterminada para extraer eventos de dicha imagen. Para cada evento, busca sus réplicas y a partir de allí recupera el histograma del valor central. Una vez los eventos y sus asociados valores centrales son extraídos de la imagen, SNESIM los almacena en una estructura dinámica llamada "Árbol de búsqueda" [24].
Cuando los datos obtenidos de la imagen (o imágenes) son almacenados, SNESIM sigue el diagrama de flujo de la SEC, visitando y simulando cada nodo sin información usando un camino aleatorio; la simulación es hecha basada en los datos que provienen de la imagen de entrenamiento y los nodos anteriormente simulados. SNESIM reproduce la imagen de entrenamiento, pero también puede honorar datos como pozos (datos duros) o interpretación de líneas sísmicas (datos blandos).
Los datos duros son incorporados en simulaciones basadas en el concepto del semivariograma usando krigeado, sin embargo, MPS logra incorporar el condicionamiento de este tipo de datos a través del uso de imágenes de entrenamiento completas que representan los datos duros disponibles. En la práctica, eso significa que se debe generar una imagen a partir de datos provenientes de pozos para poder incorporarlos en la simulación.
Los datos blandos típicamente se refieren a datos extensivos obtenidos a partir de mediciones indirectas, por esta razón, representan una vista filtrada de la subsuperficie. Los métodos tradicionales integran datos de esta clase usando algún tipo de co-krigeado [13], el cual se fundamenta en conceptos estadísticos puros sin tener en cuenta las relaciones físicas, ya que sólo usa variogramas (uno proveniente de la variable simulada, otro de los datos blandos y el otro a partir de el variograma cruzado) para definir la estructura. La aplicación de esta metodología en modelación 3D posee grandes dificultades, por lo tanto la MPS propone un condicionamiento diferente usando la codificación de los datos blandos en términos de las probabilidades a priori o usando Métodos de Clusters. Luego que las probabilidades a priori son calculadas, son combinadas con las probabilidades provenientes de los datos duros las cuales son leídas usando la misma metodología que en las imágenes de entrenamiento [1].
Para la integración de los datos duros y datos blandos han surgido muchas aproximaciones, la mayoría de ellas basadas en el principio de independencia de eventos, el cual en la practica no se cumple. Por tanto, modernos algoritmos basados en MPS usan un nuevo principio llamado el Modelo ξ [4], expuesto brevemente en la siguiente sección.
Modelo ξ
En la mayoría de problemas que envuelven la modelación de aguas subterráneas es necesario calcular la probabilidad condicional de un evento (A) si otros (B,C) son conocidos, es decir, Prob (A|B,C). En este problema particular, P(A) representa la probabilidad de ocurrencia de una facie; y B y C, la probabilidad de tener una litología a partir de información obtenida de pozos o de interpretaciones sísmicas respectivamente. Generalmente estos eventos no son independientes entre sí:
Suponiendo que la determinación de las probabilidades condicionales Prob (A|B) y Prob(A|C) se puede hacer fácilmente, combinar estas dos es la probabilidad condicional requerida Prob(A|B,C). La solución de este problema se basa en la denominada permanencia del incremento de la contribución. Este principio establece que "el incremento de la contribución relativa del evento C en la reducción (o aumento) de la distancia a la ocurrencia del evento A es independiente del evento B".
Antes de entender el principio anterior, es necesario establecer la forma como se determinan las distancias entre eventos, para lo cual se tienen que considerar relaciones entre probabilidades. Por ejemplo, la relación a definida de la forma:
Mide la distancia relativa a la ocurrencia del evento A, ya que:
a = 0 cuando Prob(A) = 1, eso significa cuando A ocurre.
a = ∞ cuando Prob(A) = 0, eso significa cuando A no ocurre.
De igual forma se pueden definir relaciones para el caso de las probabilidades condicionales:
b es la distancia relativa actualizada por la información B, c es la distancia relativa actualizada por el conocimiento de la información C, y x es la distancia relativa actualizada por los dos eventos B y C. En este caso el problema es la evaluación de x y por consiguiente de Prob(A|B,C) a partir del conocimiento de las relaciones a, b y c.
La contribución relativa del evento C en el evento A antes de conocer el evento B está dada por la relación (c-a/a), y la contribución de C después de conocer B seria (x-b/ b) , de tal forma que si la contribución relativa de C no depende de B entonces debe ser la misma en las dos relaciones anteriores, con lo cual se cumple:
por consiguiente:
de la ecuación 9 se deriva que:
La ecuación inicial 4 expresa la independencia del evento B en la contribución relativa de C (x/ b). Sin embargo, en algunas oportunidades puede resultar de interés introducir esta dependencia haciendo que el lado derecho de la ecuación 4 dependa de B. Esto se logra por medio de un exponente que depende de B de la siguiente forma:
Donde τ (B, C) es un parámetro que mide la contribución relativa de información del evento C con respecto al B, y de ahí proviene el nombre de Modelo Tau. Este exponente depende tanto de B como de C y si tau > 1 el término c/a tiene una mayor importancia, es decir, se incrementa la contribución del evento C. En el caso tau < 1 la contribución de C disminuye y cuando tau = 0 se obtiene que x = b y por lo tanto Prob(A|B,C) = P(A|B), de lo cual se desprende que este modelo es completamente diferente a las suposiciones de independencia e independencia condicional que usualmente se invocan para derivar las probabilidades condicionales de interés.
Estos pesos (B,C) permiten determinar la redundancia de la información, es decir, si el evento B tiene información que también está incluida en el evento C, por lo tanto su determinación resulta de interés práctico. Las metodologías para la determinación de estos pesos se explican en [18]. Este modelo resulta especialmente apropiado para la integración de información de la interpretación sísmica en los procedimientos de generación de mapas, ya que el evento C podría corresponder a la litología medida en los pozos cercanos, mientras que el evento B sería información proveniente de la interpretación geológica o sísmica.
Simulaciones y discusión
En este estudio se ha modelado un acuífero parcialmente confinado con un área aproximada de 4200 km2, representado conceptualmente en un rectangulo de 8,5 km en el eje X, 5,0 km en el eje Y y 4,8 km de profundidad (En la figura 3 se puede observar el rectángulo que representa el área de estudio). Esta región está asociada a una zona alternativamente seca y húmeda con coberturas que varían entre bosques secundarios, algunos pequeños relictos de bosques primarios y pastizales predominantes. Su clima está caracterizado por una alta precipitación (Precipitación Media Anual Multianual = 1150mn) y una alta temperatura (alrededor de 28oC). La hidrografía en esta área comprende solo pequeños arroyos intermitentes los cuales tienden a desaparecer durante gran parte del año. Solamente los arroyos Grande de Corozal y Morroa eventualmente permanecen todo el año.
El acuífero Morroa está formado de areniscas y conglomerados poco consolidados intercalados con arcillolitas. Aunque ha sido imposible determinar la conformación del acuífero debido a su gran variabilidad espacial, se puede decir que éste yace sobre una formación impermeable con presencia de estratos de limonitas y areniscas muy espaciadas contenidas en una matriz predominantemente arcillosa. Los estratos suprayacentes muestran una diversidad espacial que impide una generalización. Para definir los límites del Acuífero, se examinaron cambios en las estructuras de facies las cuales sufren notables transformaciones repentinas de arena a arcilla, como lo muestran los esquemas geológicos del área de recarga mostrados por [5]. El límite oriental del acuífero fue definido a través del análisis de las líneas sísmicas [7] por medio del cual se identificó una "extinción abrupta de la formación". Finalmente, el límite noroccidental está determinado por afloramientos presentes en el área.
Generalmente, las facies son determinadas a partir de análisis que incluyen perfiles litológicos extraídos de pozos, información geofísica e interpretaciones sísmicas, de suerte que, los modelos conceptuales hidrogeológicos se han construido usando interpretaciones geológicas que dependen sólo de la subjetividad de una persona. En esta aproximación se introduce una herramienta que permite involucrar la incertidumbre en la modelación hidrogeológica, por medio de la generación de múltiples simulaciones del acuífero, las cuales reproducen de manera fiel las propiedades estadísticas de los datos; además, se determina una probabilidad de ocurrencia de arenas en cada elemento de la malla que representa el área de estudio. El tamaño de las celdas simuladas en la malla fue definido como 500 m en y, 850 m en x y 40 m en profundidad(z), teniendo en cuenta el tamaño del área de estudio. De esto resulta una malla con 1.200.000 celdas(100 en X,Y y 120 en profundidad) para el procesamiento.
La información disponible es insuficiente, difusa y fraccionada, adicionalmente está compuesta por parámetros imprecisos. Por lo anterior, es indispensable el uso de todos los datos, incluso los incompletos; para este fin es necesario desarrollar una etapa de pre-procesamiento de los datos. En la primera etapa del pre-procesamiento, se construyeron gráficos con los datos duros obtenidos a partir de algunas interpretaciones de pozos en la zona de recarga del Acuífero, esta información sólo se refiere a los primeros 200 m de profundidad. En este paso, se asignaron probabilidades de ocurrencia a cada celda que conforma la interpretación: se asignó un valor de 1 donde hay presencia de arenas y 0 donde hay presencia de arcillas, debido a que ésta información es asumida como cierta.
En la segunda etapa, fue necesario convertir las interpretaciones sísmicas que cubrían toda el área de estudio en gráficos aplicables al modelo usado, este paso requiere el uso de una rutina semiautomática basada en la transformación de dibujos escalables en imágenes digitales malladas (Figura 2). Esas imágenes fueron digitalizadas asignando valores de probabilidad de entre 0,8 y 0,9 en los lugares donde se observó la presencia de arenas, y de 0,1 a 0,2 donde arcillas fueron distinguidas. En los lugares donde se encontraron intercalaciones se usaron los valores de las proporciones.
Figura 2 Preprocesamiento de imágenes provenientes de interpretación de líneas sísmicas
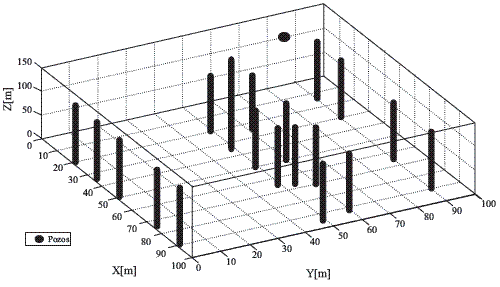
Adicionalmente, la escasez de pozos profundos con información medida configura un problema para calcular las variables necesarias para el uso de las metodologías geostadísticas propuestas. Para resolver esta problemática se introduce el concepto de pozos simulados, los cuales se generan a partir de la información proveniente de las líneas sísmicas incompletas (líneas que aunque están en el área de estudio no la cubren completamente). De las líneas mencionadas se simularon 18 pozos, los cuales se asumieron como datos blandos, por tanto se asignaron valores de 0,9 para las arcillas y 0,1 para las arenas. Conjuntamente con los dos pozos profundos y los cortes geológicos originales, los pozos simulados conforman la totalidad de los pozos disponibles (Figura 3).
Figura 3 Pozos hidráulicos usados en la modelación
Después del pre-procesamiento, se realizaron los cálculos geoestadísticos necesarios para la construcción de los modelos de simulación definitivos. Los semivariogramas fueron calculados mediante el uso del software S-Gems a través de ajustes gráficos del Rango, la Meseta y el Efecto Pepita.
Con la intención de comparar los resultados obtenidos, se llevaron a cabo dos procesos:
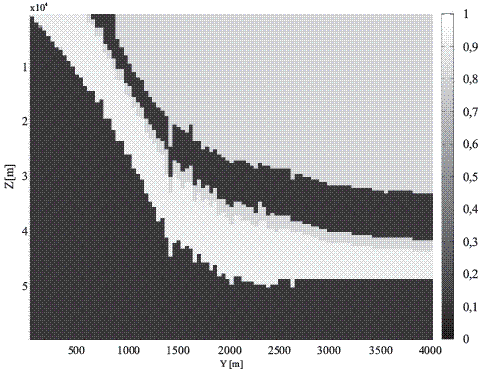
Primero, se implementó la Simulación Secuencial Indicador (SISIM), la cual fue propuesta por [25], modificada por [26], con el propósito de utilizar datos blandos. En este orden de ideas, se generaron 400 realizaciones, ya que este número permite encontrar un buen equilibrio entre obtener una aproximación confiable de la interpretacón estocástica del Acuífero y tiempos de procesamiento asociados a los recursos computacionales disponibles. Finalmente, para el análisis del resultado de las realizaciones se generaron mapas de probabilidades de los valores esperados (E), usando POSTSIM [13]. Los valores encontrados oscilan entre 1, correspondiente a la máxima probabilidad de ocurrencia de arenas, y 0 a la mínima (Figura 5).
Segundo, se simularon las unidades hidroestratigráficas usando el Modelo ξ, los datos blandos y los datos duros fueron incorporados en el modelo, sin embargo, es imperativa la construcción de una imagen a priori que establezca la probabilidad de ocurrencia de arenas y que a la vez permita integrar los datos condicionantes. Para desarrollar esta tarea se utilizaron dos métodos de interpolación ampliamente aceptados: a) interpolación en 3D usando krigeado y b) inverso de la distancia. A pesar de que los resultados obtenidos no son satisfactorios, toda vez que la información fuerte (pozos) existente es muy deficiente, se decidió utilizar el modelo generado por el segundo método.
Figura 4 Resultados de las simulaciones obtenidas usando SISIM (Probabilidad de Ocurrencia de arenas promedio a partir de 400 simulaciones)
En este trabajo, se realiza un análisis de sensibilidad para encontrar el valor de ξ, de manera que, se utilizaron valores de 0,1, 0,6, 1, 1,6, 2. Aunque no se observó una variación considerable en los resultados obtenidos se optó por asignar un valor de 0,6 con el fin de dar mayor relevancia a la información blanda que la generada usando inverso de la distancia.
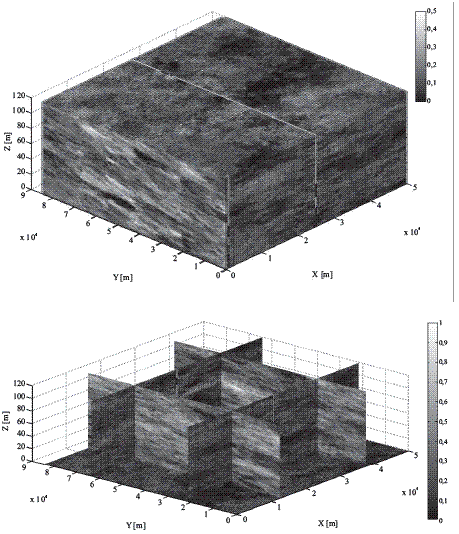
Para generar las simulaciones, se usa la rutina nnetcombindsim, que es la primera versión en Fortran, del código desarrollado por [2] basado en el algoritmo original SNESIM, para esto, se asigna B a las interpretaciones sísmicas (datos blandos) y C a la interpolación hecha a partir de los pozos tanto reales como simulados (datos duros). En este punto, es importante recalcar que se le ha dado mayor significancia a los datos blandos debido a la notable ausencia de datos duros. Los resultados obtenidos muestran una gran dispersión, por esta razón se agruparon en dos categorías: a) probabilidades mayores a 0,85 en el grupo1 y b) probabilidades menores en el grupo 2. Esta agrupación permite inferir los resultados de una mejor manera. Figura 5 muestra los resultados obtenidos.
Figura 5Visualización 3D de los resultados del Modelo t (gris oscuro: Grupo 1, gris claro: Grupo 2)
En este punto, es importante mencionar que los resultados obtenidos a partir del uso de la Simulación Estocástica Condicional son mucho mas consistentes, ya que representan de mejor manera la variabilidad asociada a las formaciones hidroestratigráficas presentes en el área de estudio, que los resultados obtenidos por el método de Geoestadística de puntos Múltiples, los cuales muestran una gran dispersión de las probabilidades de arena causadas por la imprecisión introducida al modelo a través de la interpolación.
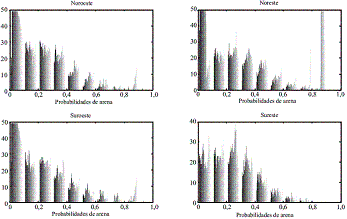
Consecuentemente con lo anterior, los resultados obtenidos por la SEC son usados para la definición de zonas con mayor probabilidad de ocurrencia de arenas, y por lo tanto más aptas para la explotación hídrica. Este análisis es desarrollado a través de la división del área de estudio en 4 unidades superficiales, nombradas de acuerdo a su ubicación geográfica relativa (Noroeste, Noreste, Suroeste y Sureste), asociadas con 3 diferentes rangos de profundidad desde la menor a la mayor profundidad (Rango 1:0-500 m. Rango 2:500-2000 m. y Rango 3: 2000-4000 m) de tal manera que se obtienen 12 subdivisiones. Para cada subárea, el histograma de la probabilidad de ocurrencia de arenas es construido, con la intención de establecer áreas estratégicas de explotación. En la figuras 6-8 se muestran los resultados de los histogramas para las 4 unidades superficiales y para cada una de los rangos de profundidades establecidos.
Figura 6 Histograma de probabilidades de Arena de las 4 unidades superficiales para los primeros 500 m de profundidad
Conclusiones
Los datos tenidos en cuenta originalmente para el desarrollo de esta investigación están representados en dos líneas sísmicas que cubren longitudinalmente la extensión del acuífero localizadas en la zona central y tres pozos con una profundidad mayor a 2000 m, adicionalmente fueron generados 18 pozos a partir de las líneas sísmicas que no cubrían la totalidad del acuífero, lo cual configuró un escenario complejo debido a la escasez evidente de datos. A pesar de esta insuficiencia, y gracias a la integración de datos duros y blandos, se obtuvo una acertada representación de las unidades hidroestratigráficas que conforman el Acuífero. Esta integración, establece la única alternativa para la construcción de modelos hidrogeológicos conceptuales en hidrosistemas complejos, en donde la información es la principal limitante. Por lo tanto, la utilización de la Simulación Estocástica Condicional y Geostadística de puntos múltiples conjuntamente con el Modelo ξ, como metodología para este tipo de casos, cobra vital importancia en el proceso de integración de la información, ya que evita la presunción de independencia de eventos y a la vez, permite la completa caracterización del área de estudio.
El modelo conceptual del Acuífero Morroa generado permite describir la variabilidad estratigráfica, no sólo de la zona de recarga sino también de la extensión total, a través de la determinación de las probabilidades de ocurrencia de facies asociadas a arenas y a arcillas, lo que a su vez ayuda a determinar cuantitativamente la conductividad hidráulica (Ks). La determinación de las probabilidades se logró a través del cálculo de la esperanza matemática(E) de múltiples realizaciones generadas conservando las propiedades geoestadísticas de los datos originales. El valor obtenido está asociado a la probabilidad de que una celda particular represente una formación arenosa; lo que quiere decir que valores bajos representan materiales arcillosos, normalmente asociados a conductividades bajas que constituyen usualmente acuitardos, mientras que valores altos representan materiales arenosos con conductividades altas, que conforman normalmente acuíferos. De esta manera, el modelo es capaz de reproducir tendencias de canales, el espesor de las formaciones en la mayoría de las regiones y en algunas los cambios en el azimut.
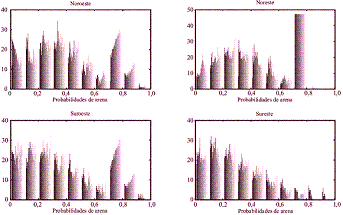
Figura 7 Histograma de probabilidades de Arena de las 4 unidades superficiales para profundidades entre 500 y 2000 m de profundidad
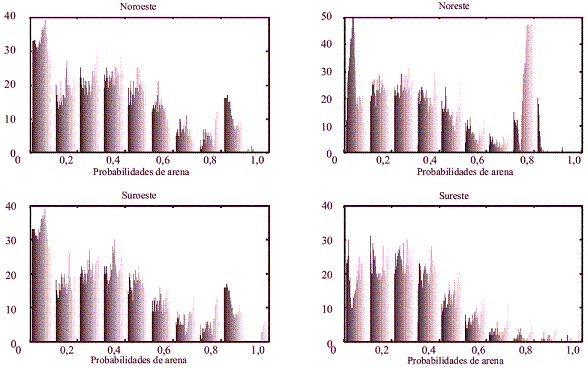
A partir de los histogramas generados, se puede establecer que la zona noreste del aquifero, y mas específicamente los primeros 1000 metros de profundidad, representa un sitio adecuado para la explotación de recursos hídricos, ya que presenta una facie caracterizada por altas probabilidades de ocurrencia de arena; en contraste la zona sureste presenta una facie arcillosa y poco explotable. Las zonas al oeste (norte y sur) presentan una distribución mas heterogénea, y por consiguiente existe una mayor incertidumbre en términos de su explotación.
Esta investigación es de gran utilidad en la determinación estratégica de lugares aptos para la instalación de pozos de extracción, ya que con el modelo desarrollado se puede establecer no sólo areas de explotación, sino también el grado de incertidumbre asociado a fuentes de agua subsuperficial (arenas), lo que representa un logro en el diseño de políticas en áreas donde la escasez de agua es un problema creciente.
Figura 8 Histograma de probabilidades de Arena de las 4 unidades superficiales para profundidades entre 2000 y 4800 m de profundidad
A pesar de la capacidad del modelo para representar el área de estudio, se encontraron ciertas limitaciones para reproducir las zona suroriental, debido a la ausencia notable de pozos de extracción monitoreados en esta área. Esta problemática puede ser aliviada a través de campañas de monitoreo. Por otro lado, fue imposible la introducción de la información relacionada con la génesis de las formaciones, como quiera que se tuvo una serie de dificultades en el proceso de transformación de estos antecedentes en datos consolidados. Por tanto, se recomienda desarrollar una aproximación que ayude a la integración de estos antecedentes en el modelo, algunos estudios recientes sugieren el uso de probabilidades transicionales en la introducción de procesos deposicionales.
Referencias
1. S. Strabelle. Sequential Simulation Drawing Structures from Training Images. Stanford Center for Reservoir Forecasting. 13th Annual Meeting, Stanford, USA.2000 .pp .12O. [ Links ]
2. García-Cabrejo. Metodologías de modelamiento en hidrociencias integrando geoestadistica y redes neuronales artificiales. Tesis para optar al titulo de Magíster en Hidrosistemas, Pontificia Universidad Javeriana. 2008. pp.176. [ Links ]
3. N. Remy. Geostatistical Earth Modeling Software:User's Manual. Stanford University. 2004. pp 87. [ Links ]
4. A. G. Journel. "Combining knowledge from diverse sources: An alternative to traditional conditional independence hypothesis". Mathematical geology. Vol. 34. 2002. pp. 573-596. [ Links ]
5. J. Buitrago, L. Donado. Evaluación de las condiciones de explotación de la zona de recarga del Acuífero Morroa. Departamentos de Sucre y Córdoba (Colombia). Proyecto de Grado para optar al título de Ingeniero Civil. Facultad de Ingeniería. Universidad Nacional de Colombia. Bogotá. 2000. pp. 200. [ Links ]
6. D. Pacheco, P. Villegas. Caracterización hidráulica del Acuífero Morroa utilizando pruebas de bombeo. Proyecto de Grado para optar al titulo de Ingeniero Civil. Facultad de Ingeniería. Universidad de Sucre. Sincelejo. Colombia. 2003. pp. 100. [ Links ]
7. Y. Abreu. Determinación de la geometría del Acuífero de Morroa y localización de futuras zonas de posible exploración y explotación del acuífero, mediante el uso de líneas sísmicas y pozos de petróleo. Informe 015-06-05. Ministerio de Ambiente Vivienda y Desarrollo Territorial. Junio 2005. pp . 320. [ Links ]
8. W. M. Telford, L. P. Geldart, R.E. Sheriff. Applied Geophysics. Cambridge University Press. Cambridge.1990. pp. 770. [ Links ]
9. N. Copty. Y. Rubin. G. Mavko. "Geophysicalhydrological identification of field permeabilities through Bayesian updating". Water Resources Res. Vol. 29. 1993. pp. 2813-2825. [ Links ]
10. S. K. Upadhyay. Seismic Reflection Processing: With Special Reference to Anisotropy. Ed. Springer. Londres.2004. pp. 636. [ Links ]
11. A. G. Journel, E. Isaaks. Conditional indicator simulation: Application to a Saskatchewan uranium deposit. Mathematical Geology. Vol. 16.1984. pp. 34. [ Links ]
12. J. Caers, L. Feyen. Multiple-point geostatistics: a powerful tool to improve groundwater flow and transport predictions in multi-modal formations. Stanford University. Department of Geological and Environmental Sciences. Stanford. USA. 2000. pp . 11. [ Links ]
13. C. Deutsch, A. G. Journel. GSLIB: Geostatistical Software Library and User's Guide. Applied Geostatistics Series. 2a ed. Oxford University Press. Oxford.1998. pp. 340. [ Links ]
14. A. Journel, F. Alabert. New method for reservoir modeling, Journal of Petroleum technology. Vol 42. 1990. pp 212-218. [ Links ]
15. B. Arpat. Sequential Simulation with Patterns. Disertación Doctoral. Universidad de Stanford. 2005. pp. 160. M. Anderson. W. Woessner. Applied Groundwater Modeling. Academic Press. Inc. San Diego (CA). 1992. pp. 380. [ Links ]
16. D. G. A. Krige. Statistical approach to some basin mine valuation problems on the Witwatersrand, J. Chem Metall and Min. Soc. South Africa. Vol. 52. 1951. pp 119-139. [ Links ]
17. G. Matheron. Principles of Geostatistics, Economy Geology. Vol. 58. 1963. pp. 1246-1266. [ Links ]
18. S. Krishnan, A. Boucher, A. Journel. "Evaluating information redundancy through the tau model". Geostat 2004 Proceedings. 7th International Geostatistic Congress. Banff (Canada). 2004. pp. 1037-1046 [ Links ]
19. C. Farmer. "Numerical rocks". P. King (editor) The mathematical generation of reservoir geology. Clarendon Press. Oxford.1990. pp. 22-33. [ Links ]
20. C. Deutsch. "Fortran programs for calculating connectivity of three dimensional numerical models and for ranking multiple realizations". Computer and Geosciences. Vol. 24. 1998. pp. 69-76. [ Links ]
21. H. Tjelmeland. Stochastic Models in reservoir characterization and Markov random fields for compact objects. Disertación doctoral. Universidad de Ciencia y Tecnología. Noruega. Vol 44. 1996. pp. 100. [ Links ]
22. J. Caers, A. Journel, Stochastic reservoir simulation using neural networks trained on outcrop data. SPE Annual Technical Conference and Exhibition. 1998. pp. 321-336. [ Links ]
23. P. Goovaerts. Geostatistics for Natural resources evaluation. New York: Oxford University Press. 1997. pp. 483. [ Links ]
24. D. Knuth. Art of Computer Programming. 2a ed. Addison-Wesley Pub. Co. Reading(MA). 1998. pp. 896. [ Links ]
25. R. M. Srivatasa. An Application of Geostatistical Methods for Risk Analysis in Reservoir Management. Society of Petroleum Engineering. SPE 20608. 1990. pp . 825-834. [ Links ]
26. S. A. McKenna. Utilization of soft data for uncertainty reduction in groundwater flow and transport modeling. Golden, CO. Colorado School of Mines. PhD dissertation.1994. pp 150. [ Links ]
(Recibido el 17 de septiembre de 2008. Aceptado el 26 de mayo de 2009)
*Autor de correspondencia: teléfono: + 57 + 1 + 338 49 60, fax: + 57 + 1 + 338 49 60, correo electrónico: anibaljoseperez@yahoo.com (A.Pérez).