Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230On-line version ISSN 2422-2844
Rev.fac.ing.univ. Antioquia no.50 Medellín Oct./Dec. 2009
Discusión de operadores involucrados en un proceso de calibración mediante algoritmos genéticos para un modelo de calidad del agua de corrientes superficiales trabajando con la herramienta Qual2Kw
Discussion of operators involved in a process of calibration using genetic algorithms for a surface water quality model to work with the tool Qual2Kw
Ismael Leonardo Vera Puerto1*, Jaime Andrés Lara Borrero2
1Grupo de Investigación Biotecnología Ambiental. Centro de Ciencias Ambientales EULA-Chile. Universidad de Concepción. Barrio Universitario Casilla 160 C S/N. Concepción, Chile.
2Grupo de Investigación Ingeniería Sanitaria y Ambiental para el Desarrollo (ISAD). Facultad de Ingeniería, Departamento de Ingeniería Civil. Pontificia Universidad Javeriana. Calle 40 No 5-50, Piso 1. Edif. José Gabriel Maldonado S.J. Bogotá, Colombia.
Resumen
Al inicio del proceso de calibración de un modelo de calidad del agua, empleando la herramienta computacional Qual2kw que incluye un algoritmo genético como herramienta matemática para calibración, es necesario introducir algunos operadores para el inicio del proceso de calibración que busca la mejor combinación de constantes que representen la realidad de la corriente en cuanto a su calidad de agua. En este trabajo, se realizan recomendaciones generales sobre tres operadores que utiliza el algoritmo genético: la semilla empleada, el número de generaciones y el número de poblaciones; principalmente estos dos últimos resultan importantes, porque implican tiempos computacionales asociados, puesto que una combinación que genere muchas corridas podría no presentar variaciones significativas en el ajuste total del modelo, de tal manera que una combinación óptima podría dar buenas soluciones en tiempos razonables. Este trabajo encuentra que efectivamente hay puntos donde la mejora en la calidad del ajuste no aumenta más de un 5% en variación al valor obtenido por la función de error. Por tanto, es posible recomendar ciertos valores para emplear por parte del modelador al momento de emplear esta herramienta.
Palabras clave: algoritmos genéticos, calibración, modelo de calidad del agua, Qual2Kw.
Abstract
At the beginning of the process of calibration of a water quality model, using the computational tool Qual2kw that includes a genetic algorithm as a mathematical tool for calibration, it is necessary to introduce some operators for the start of the calibration process that seeks the best combination of constants that represent the reality of the current in terms of water quality. In this work are made general recommendations on three operators that uses genetic algorithm: the seed used, the number of generations and the number of populations; mainly the latter two are important because they involve partners computational times, since a combination that creates many runs could not present significant variations in the total adjustment of the model, so that a combination optimal could give good solutions in reasonable time. This study found that indeed there are points where the improvement in the quality of adjustment does not increase more than 5% variation in the value obtained by the function of error, so it is possible to recommend certain values for use by the modeler at the time of use this tool.
Keywords: genetics algorithms, calibration, water quality model, Qual2Kw.
Introducción
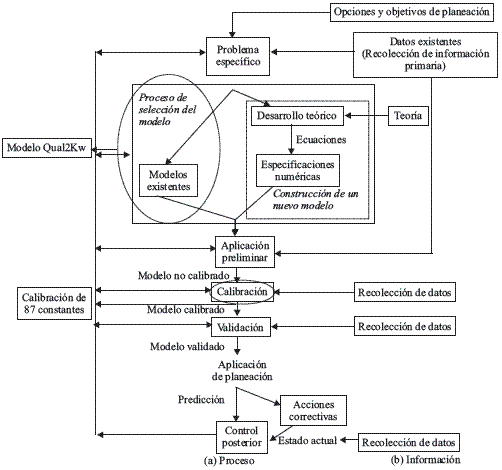
El agua es esencial para la vida en la tierra y cambios en su calidad natural, originan impactos ecológicos que algunas veces pueden ser devastadores [1]. Para ello, el objetivo básico de la ingeniería de la calidad del agua busca la determinación de controles (parámetros o índices) de contaminación para cumplir un objetivo de calidad ambiental específico [2], apoyándose en la simulación mediante modelos que representan de la mejor forma posible la realidad de una corriente en condiciones iníciales y en condiciones posteriores a una intervención antrópica. El proceso de modelación ambiental se muestra en la figura 1, donde el paquete computacional empleado es integrado en el marco conceptual propuesto. De esta forma, un modelo de calidad del agua para una corriente superficial interacciona una serie de procesos físicos, químicos y biológicos, que involucra el empleo de constantes necesarias que le permiten representar de forma aproximada el comportamiento de una corriente. Estas constantes pueden ser determinadas de forma experimental o mediante un proceso matemático de calibración, siendo las metaheurísticas, las herramientas importantes para la estimación de estos valores en forma matemática. En el presente artículo, se utiliza para calibración del modelo de calidad del agua, el modelo QUAL2Kw [3], que incorpora el algoritmo genético PIKAIA [4] para la calibración de las constantes.
El algoritmo genético, se enmarca como una técnica de búsqueda basada en los mecanismos de la genética natural y operaciones biológicamente inspiradas [6], que involucra una serie de operadores que le permiten converger para encontrar la mejor solución posible, pero encontrar el conjunto de operadores que logren que el algoritmo genético trabaje y encuentre, sin que el proceso computacional emplee demasiado tiempo, el juego de constantes que mejor represente la realidad del río, implica el primer reto al cual debe enfrentarse el modelador al inicio de la calibración de su modelo de calidad del agua cuando utiliza esta herramienta. La aplicación de esta técnica de optimización en modelos de calidad del agua sobre corrientes superficiales, han sido reportados previamente [3, 7, 8, 9] obteniéndose buenos resultados, pero de acuerdo a lo planteado en [6], el análisis sobre operadores del algoritmo, tales como: la probabilidad de cruzamiento, el tamaño de las poblaciones empleadas, el número de generaciones, conducirán a una mejor aplicación de esta técnica en la calibración de modelos de calidad del agua.
Figura 1 Proceso completo de modelación ambiental integrando la información necesaria y la implementación efectiva para aplicaciones de control. Adaptado de [5]
El objetivo de este trabajo es intentar entregar recomendaciones sobre el uso de tres operadores del algoritmo genético, sobre los cuales se han realizando múltiples ensayos, ellos son: la semilla empleada, el número de generaciones, y el número de poblaciones, aplicadas a varias corrientes, para permitir la uniformidad en la recomendación de los rangos a utilizar para estos operadores.
Experimentación
Se trabajó sobre tres corrientes principales que atraviesan la zona urbana de Bogotá D.C., el Río Fucha, el Río Salitre y el Canal Torca-Guaymaral. La ciudad de Bogotá se encuentra ubicada a una altitud promedio de 2600 m.s.n.m. con una temperatura ambiental media anual de 14oC. Las tres corrientes que se mencionan anteriormente nacen en los cerros orientales de la ciudad en alturas superiores a los 3000 m.s.n.m, y los tramos considerados para realizar el modelo corresponden a las partes urbanas de las corrientes que presentan tramos canalizados en concreto y tramos en tierra, de acuerdo a la información recolectada en los archivos de la Empresa de Acueducto y Alcantarillado de Bogotá. Estos tramos se caracterizan por poseer bajas pendientes, dada la topografía de la altiplanicie Cundiboyacense donde se emplaza la capital colombiana, y cuyos cauces desembocan finalmente sobre el río Bogotá. La información de calidad del agua en cuánto a parámetros evaluados sobre las corrientes de estudio, y los afluentes a cada una de las mismas, fue suministrada por la Pontificia Universidad Javeriana, en el marco del convenio interadministrativo de cooperación e investigación, que se desarrolló entre la Empresa de Acueducto y Alcantarillado de Bogotá, el Dama y la Universidad, denominado Evaluación del sistema hídrico de Bogotá con fines de establecer lineamientos respecto al grado de calidad, posibles usos y saneamiento gradual e integral en algunos puntos o tramos en las principales cuencas del distrito capital.
Los modelos fueron armados para cada corriente de manera independiente dentro de la plataforma Qual2kw. Los valores y criterios de selección para este trabajo, sobre los operadores necesarios a ser introducidos por el modelador cuando emplea el algoritmo genético PIKAIA, se resumen en la tabla 1.
Tabla 1 Operadores del algoritmo genético PIKAIA y criterio de selección
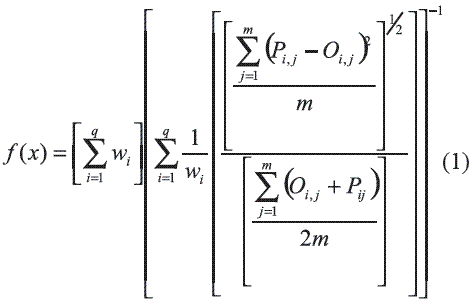
Una vez definidos los operadores del algoritmo genético, fue necesario definir la función objetivo. Para evaluar el ajuste de cada uno de los parámetros de calidad del agua en la calibración del modelo QUAL2Kw la función empleada es similar a la recomendada por Pelletier y colaboradores [3], que es una ecuación robusta que representa todas las variables del modelo. Esta función de ajuste es el recíproco del peso promedio (pondera las variables que mas influyen en el proceso) de la normalización de la raíz cuadrada del error de la diferencia entre los datos obtenidos con el modelo y los datos de campo y se representa en la ecuación 1. Se tomó el recíproco de esta función porque es importante mencionar que el algoritmo genético PIKAIA maximiza la función objetivo. Una característica que debe tener una función de ajuste para un algoritmo genético es que esta debe ser capaz de castigar a las malas soluciones, y de premiar a las buenas, de forma que sean estas últimas las que se propaguen con mayor rapidez.
Donde:
Oi,j = Valor observado
Pi,j = Valor predicho por el modelo
m = Número de pares de valores observados y predichos
wi = Factor de peso
qi = Número de variables de estado
En la ecuación 1 existe un factor de peso para cada una de las variables modeladas (en este estudio se trabajo con pH, Temperatura, Oxígeno Disuelto, CDBO fast (DBO5), CDBO slow (DBO filtrada), SSI (trabajados como sólidos suspendidos totales), y Generic Constitutent (trabajado como DQO)); para la calibración del modelo, esta se realizó considerando en una primera etapa, pesos iguales para cada una de las variables, y en una segunda etapa, pesos diferentes. En esta última fase, se consideraron los parámetros de calidad del agua de mayor importancia que involucran el consumo de oxígeno, ya que tienen un mayor peso en comparación al resto de de los parámetros.
Las corridas del programa para cada uno de los valores que se desean recomendar se llevaron a cabo de la siguiente forma para las tres corrientes:
Semilla: inicialmente se hacen pruebas con diferentes semillas, éstas son generadas de forma aleatoria usando la función presente en Microsoft Excel, la cual utiliza una semilla fija a diferencia de la trabajada en el modelo QUAL2Kw que corre en Fortran. Las semillas son iguales en las tres pruebas que se hacen sobre cada corriente, pero varían con respecto a las empleadas en las otras corrientes, de esta manera se amplia el margen de encontrar mejores soluciones.
Número de generaciones: para correr el programa, se selecciona la semilla que presentó el mejor ajuste, y se hacen pruebas hasta un total de 200 generaciones para el caso del río Fucha, 120 generaciones para el río Salitre y 200 generaciones para el canal Torca Guaymaral, y como se verá más adelante en la figura 3, para pesos iguales se variaron estos valores para mirar el comportamiento de este parámetro; se deja fijo el número de poblaciones a 4. La decisión de trabajar con el menor número de generaciones para el caso del río Salitre, se debe a que los costos computacionales para esta corriente eran más altos, dado que el modelo de esta corriente incluía mayor cantidad de tramos o secciones de río para modelar, lo cual afecta de forma directa el proceso de resolución de las ecuaciones diferenciales, traducido en mayores tiempos computacionales en la etapa de calibración.
Número de poblaciones: para correr el programa se aumentó el número de poblaciones de forma par iniciando en 2 y terminando en 100, en todos los ríos modelados. Debido a los altos tiempos computacionales, el número de generaciones fue fijado en 4, trabajando en cada corriente con la semilla que presentó el mejor ajuste.
Finalmente, es importante mencionar que los rangos permitidos de variación, en el proceso de calibración, de las diferentes constantes calibradas para los parámetros de calidad del agua empleados en este trabajo, fueron tomados usando como base lo sugerido por los desarrolladores del modelo, verificando que estuvieran acordes con la revisión realizada en la referencia [11].
Resultados y discusión
En las figuras 2, 3 y 4 se presentan los resultados obtenidos respecto a cada uno de los operadores que se desea recomendar para el algoritmo genético PIKAIA. En el eje de las abscisas se presenta la variación de cada valor, y en el eje de las ordenadas el correspondiente ajuste logrado, utilizado como referencia para evaluar la capacidad de ajuste del modelo.
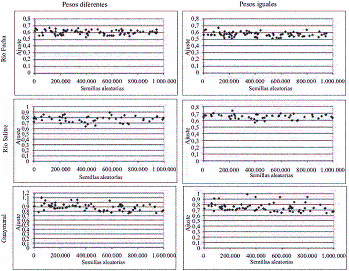
Figura 2 Comportamiento de la variación de la semilla respecto al ajuste logrado para cada corriente
En la figura 2 se puede apreciar que la dispersión de los valores de ajuste en relación a que no presenta una tendencia definida para ninguna de las tres corrientes estudiadas, permite concluir que no hay una relación directa entre la semilla seleccionada para calibrar el modelo inicialmente y el ajuste final encontrado. Sin embargo es el parámetro de los tres evaluados con mayor variación en el ajuste, llegando a mejoras en la función de ajuste en un 30%. Esto no es consistente con lo argumentado por Liu, et al [9], y Ng, et al [12], donde se comenta que algunas investigaciones previas han encontrado que al momento de cambiar la semilla el valor de la función objetivo no varía significativamente, y que únicamente la selección de la semilla resulta importante al momento de mejorar el tiempo de convergencia en la obtención de la mejor solución. Según Ng, et al [12], los resultados de su propia investigación corroboran lo argumentado en su discusión y en la referencia [9] no se establece ninguna conclusión puesto que se trabaja con algunos valores de prueba. Es interesante ver que las mejoras en el ajuste son consistentes con lo argumentado por los desarrolladores del programa y presentado en la referencia [3] donde se puede observar que la mejora en el ajuste para 10 semillas estudiadas puede alcanzar hasta un 30% a bajas generaciones pero decrece a medida que se aumenta el número de las mismas, llegando aproximadamente a un 11%. Una posible explicación para la divergencia respecto a lo reportado anteriormente, es que el número de variables involucradas para calibración en este caso es mayor a las mostradas en las referencias [9] y [12], lo que presumiblemente podría establecer que al aumentar la cantidad de constantes a calibrar, la semilla inicial comienza a cobrar importancia en la convergencia final.
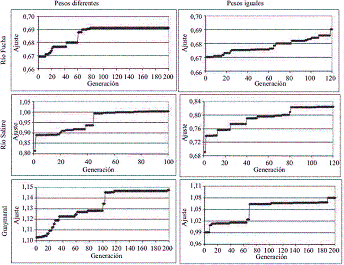
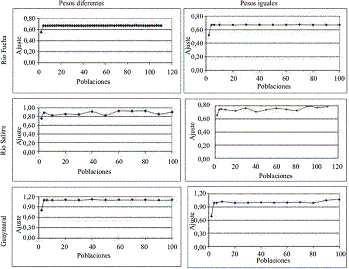
Figura 3 Comportamiento del incremento en el número de generaciones respecto al ajuste logrado para cada corriente
En la figura 3 se puede apreciar que se presentan cambios en el ajuste a medida que se incrementa el número de generaciones, esto puede ser explicado por una mayor evolución del conjunto de constantes calibradas por el modelo. Pero si se aprecia detalladamente la figura 3, se puede observar que el incremento en el valor de ajuste total logrado no presenta mayor variación porcentual entre cada mejora significativa, que puede ser estimado en un máximo de 5% entre cada mejora del ajuste. Sin embargo se observa que alrededor de 70 generaciones se obtienen mejoras en el ajuste sin un gasto computacional tan grande como el que requieren 100 generaciones, que se establece como el óptimo. Este rango de magnitud es similar a lo reportado por Liu, et al [9] con un óptimo de 100 poblaciones. Según Pelletier, et al [3], con un total de 200 generaciones se notan mejoras en el ajuste que se reducen gradualmente al aumentar el número de generaciones, sin llegar a ser conclusivas, sin embargo al analizar las gráficas se nota también que sobre 100 generaciones las mejores en el ajuste no varían significativamente. Respecto a la baja incidencia en el ajuste esto si es consistente con lo argumentado por Liu, et al [9], y Ng,et al [12], que muestran que este valor poco incide en la mejora de la función de ajuste obtenido, a pesar de ello, es importante permitir cierta evolución del algoritmo, por tanto para cada problema especifico de calibración se debe permitir cierta evolución.
Figura 4 Comportamiento del incremento en el número de poblaciones respecto al ajuste logrado para cada corriente
En la figura 4 el comportamiento de las poblaciones parece no tener una tendencia definida. En el caso del río Salitre este es oscilatorio respecto a un valor medio de ajuste obtenido, y en las graficas para el río Fucha y el canal Torca Guaymaral, después de 10 generaciones alcanza el valor máximo que puede obtener. Es por ello qué, y considerando las tres corrientes, se puede recomendar que un valor de 30 poblaciones podría ser utilizado con buena aproximación para implementar en el proceso de calibración de una corriente empleando la herramienta PIKAIA. Sin embargo analizando la figura para el río Salitre se nota que los mejores ajustes se logran empleando 70 poblaciones siendo más consistente por lo recomendado por Pelletier et al [3] donde se argumenta que valores de 100 poblaciones pueden originar tan buenas soluciones como emplear 500 poblaciones en menores tiempos computacionales. Ng et al [12] probaron tamaños de poblaciones de 125, 250, 500 y 1000, llegando a la conclusión que las variaciones en el ajuste no eran significativas y por tanto emplear un valor de 125 era aplicable para su estudio.
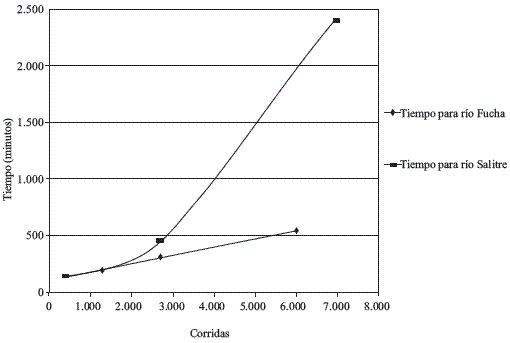
Todo esto se traduce en los tiempos computacionales empleados para correr el modelo Qual2Kw mostrados en la figura 5, donde se nota que para el modelo que presenta mayor cantidad de secciones hidráulicas (140 en total) existe un incremento exponencial de tiempo empleado para la calibración al aumentar el número de corridas, evidenciando el incremento en el consumo computacional al dar excesivos valores de poblaciones y generaciones para encontrar la mejor solución. En el caso del río Fucha (31 secciones), también mostrado, al parecer la relación lineal es la que se aplica, pero puede presentarse un posterior agotamiento computacional similar al presentado para el rio Salitre, saliéndose de lo empleado en este estudio. Ya el tema del gasto computacional para esta herramienta había sido comentado por Pelletier et al [3], que indican que para 10000 corridas se necesitan 360 minutos empleando un computador con procesador de 3,2 Ghz, y los resultados aquí mostrados se realizaron empleando un computador con procesador de 2.13 Ghz, donde por ejemplo, para el caso del río Salitre para 6960 corridas se emplean 2404 minutos. Otra característica importante observada en este estudio es la recomendación de trabajar en Microsoft Excel 2003 sin importar si se trabaja sobre Sistema Operativo Windows XP o Windows Vista, ya que cuando se experimentó trabajar con Microsoft Excel 2007, los tiempos computacionales en un simple corrida eran aproximadamente el doble de los empleados en la versión 2003.
Figura 5 Tiempos empleados para las corridas en dos de las tres corrientes trabajadas
Conclusiones
Al analizar el comportamiento de los operadores estudiados en la implementación del algoritmo genético PIKAIA, empleado por la plataforma Qual2Kw se puede inferir lo siguiente: La semilla, no exhibe un comportamiento o tendencia definida que permita afirmar que los valores enteros menores o mayores ocasionan mejores resultados, ni tampoco permite definir un criterio de cuantas semillas de prueba puedan generar el valor óptimo, lo que si se puede concluir es que se debe trabajar con la mayor cantidad de semillas posibles, y que este parámetro es el que presenta el mayor rango de variación del ajuste de las tres variables estudiadas, permitiendo inferir que es importante a la hora de la calibración; el número de generaciones tiene una influencia aunque pequeña en el proceso, si permite mejorar la calibración de este, siendo importante resaltar que siempre los valores óptimos para las diferentes corrientes se obtienen para valores superiores a 75 generaciones; el número de poblaciones presenta una variación oscilante respecto a un valor de ajuste para todas las corrientes, pero se observa que cuando se pasa de 2 a 6 poblaciones el algoritmo mejora su ajuste sustancialmente; para todas las corrientes se analiza que valores de poblaciones superiores a 70 se utilizan en la corrida óptima, esto significa que el algoritmo necesita una gran cantidad de opciones de individuos para mejorar la calibración. Finalmente, los resultados obtenidos sugieren que esta estrategia de calibración es ventajosa, aunque los costos computacionales asociados son altos, por tanto la contribución de estas recomendaciones pueden ser replicadas con estudios sobre más corrientes como por ejemplo ríos de montaña (caracterizados por presentar variaciones significativas de pendiente en forma longitudinal) y observar si el comportamiento presentado es similar al descrito para ríos de planicie en entornos urbanos como fue lo realizado en este estudio.
Referencias
1. D. A. Chin. Water quality engineering in natural systems. Ed. Jhon Wiley & Sons. Haboken. New Jersey. 2006. pp. 1-20, 124-186. [ Links ]
2. R. . Thoman, J. A. Mueller. Principles of surface water quality modeling and control. Ed. Harper Collins Publishers. New York. 1987. pp. 1-23. [ Links ]
3. G. J. Pelletier, S. C. Chapra, H. Tao. QUAL2Kw-A framework for modeling water quality in streams and rivers using a genetic algorithm for calibration. Environmental Modelling & Software. Vol 21. 2006. pp. 419-425. [ Links ]
4. T. S. Metcalfe, P. Charbonneau. Stellar structure modeling using a parallel genetic algorithm for objective global optimization. Journal of Computational Physics. Vol. 185. 2003. pp. 176-193. [ Links ]
5. S. C. Chapra. Surface Water Quality Modelling. Ed. Mc.Graw Hill. New York. 1997. pp. 235-502. [ Links ]
6. K. Chau. A review on integration of artificial intelligence into water quality modeling. Marine Pollution Bulletin. Vol. 52. 2006. pp. 726-733. [ Links ]
7. P. R. Kannel, S. Lee, Y. S. Lee, S. R. Kanel, G. J. Pelletier. Application of automated QUAL2Kw for water quality modeling and management in the Bagmati River, Nepal. Ecological Modeling. Vol. 202. 2007. pp. 503-517. [ Links ]
8. E. Aras, V. Togan, M. Berkun. River water quality management model using genetic algorithm. Environmental Fluids Mechanics. Vol. 7. 2007. pp. 439-450. [ Links ]
9. S. Liu, D. Butler, R. Brazier, L. Heathwaite, S. Khu. Using genetic algorithms to calibrate a water quality model. Science of the Total Environment. Vol. 374. 2007. pp. 260-272. [ Links ]
10. H. J. Martínez. Compresión de imágenes: un enfoque de autómatas celulares evolutivos. Tesis de grado para optar al grado de Magister Scientiarum. Universidad Centro ccidental Lisandro Alvarado. 2000. pp. 31-40. [ Links ]
11. US EPA. Rates, constants, kinetics formulations in surface water quality modeling. 2a ed. 1985. pp. 90-273. [ Links ]
12. A. W. M. Ng, B. J. C. Perera. Selection of genetic algorithm operators for river water quality model calibration. Engineering Applications of Artificial Intelligence. Vol. 16. 2003. pp.529-541. [ Links ]
(Recibido el 1 de diciembre de 2008. Aceptado el 24 de agosto de 2009)
*Autor de correspondencia: teléfono: + 56 + 41 + 220 40 77, correo electrónico: leovera82@gmail.com (L. Vera).