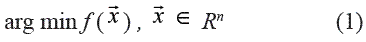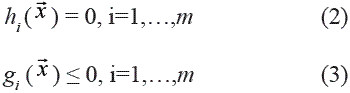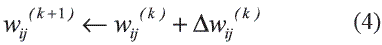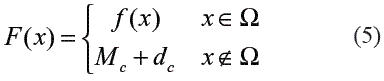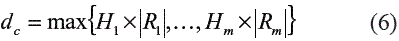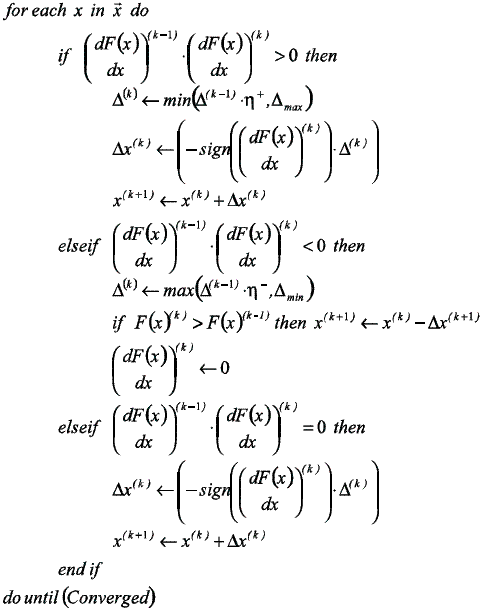Conrprop: un algoritmo para la optimización de funciones no lineales con restricciones

Conrprop: an algorithm for nonlinear optimization with constraints

Fernán Villa, Juan Velásquez^*, Patricia Jaramillo

Universidad Nacional de Colombia. Escuela de Sistemas. Grupo de Estadística Computacional y Análisis de Datos. Carrera 80 N^o 65-223, Bloque M8A, Oficina 201, Medellín, Colombia

 

---

Resumen

Resilent backpropagation (RPROP) es una poderosa técnica de optimización basada en gradientes que ha sido comúnmente usada para el entrenamiento de redes neuronales artificiales, la cual usa una velocidad por cada parámetro en el modelo. Aunque esta técnica es capaz de resolver problemas de optimización multivariada sin restricciones, no hay referencias sobre su uso en la literatura de investigación de operaciones. En este artículo, se propone una modificación de resilent backpropagation que permite resolver problemas no lineales de optimización sujetos a restricciones generales no lineales. El algoritmo propuesto fue probado usando seis problemas comunes de prueba; para todos los casos, el algoritmo de resilent backpropagation restringido encontró la solución óptima, y para algunos casos encontró un punto óptimo mejor que el reportado en la literatura.

Palabras clave: optimización no lineal, restricciones, propagación hacia atrás, rprop

 

---

Abstract

Resilent Backpropagation is a gradient-based powerful optimization technique commonly used for training artificial neural networks, which is based on the use of a velocity for each parameter in the model. However, although this technique is able to solve unrestricted multivariate nonlinear optimization problems there are not references in the operations research literature. In this paper, we propose a modification of Resilent Backpropagation that allows us to solve nonlinear optimization problems subject to general nonlinear restrictions. The proposed algorithm is tested using six common used benchmark problems; for all cases, the constrained resilent backpropagation algorithm found the optimal solution and for some cases it found a better optimal point that the reported in the literature.

Keywords: nonlinear optimization, restrictions, backpropagation, rprop

 

---

Introducción

En el caso más general, las técnicas de optimización buscan encontrar el argumento que minimiza una función f(•):

Sujeta a un conjunto de restricciones descritas como igualdades o desigualdades que deben cumplirse obligatoriamente:

Donde h_i(•) y g_i(•) son funciones que permiten describir la región factible donde se debe buscar el mínimo de f(•). Debido a que el problema general definido por (1), (2) y (3) enmarca una gran cantidad de problemas prácticos de diversa índole, se han desarrollado, durante las últimas décadas, un número importante de técnicas de optimización que dependen de la especificación particular que se le de a f(•), g_i(•) y h_i(•) [1].

El problema general definido por (1), (2) y (3) puede ser resuelto mediante métodos determinísticos o estocásticos. Los métodos determinísticos utilizan el gradiente para guiar el proceso de búsqueda, por lo que f(•) debe ser continua y diferenciable. En esencia, la dificultad de la búsqueda del punto de mínima está relacionada con la complejidad de la superficie descrita por f(•), ya que existen puntos de mínima local, regiones de gradiente prácticamente nulo, cráteres, y muchas otras irregularidades que entorpecen el proceso de optimización. El proceso se ve aún más dificultado cuando el punto de óptima debe ser buscado dentro de una región factible, ya que el algoritmo utilizado debe garantizar la exploración dentro de dicha región. La optimización de funciones no lineales utilizando técnicas basadas en el gradiente ha sido un problema tradicional en la investigación de operaciones, y existen técnicas cuyo uso ha sido muy difundido, tales como los métodos de Newton-Raphson y de descenso acelerado.

La estimación de los parámetros de redes neuronales artificiales es un caso particular de (1) en donde se desea obtener los pesos de las conexiones que minimicen una función de error, tal como el error cuadrático medio. La complejidad de este problema esta asociada a que la superficie de error puede llegar a ser bastante compleja e irregular; esta situación ha motivado la utilización de las mismas técnicas generales usadas en investigación de operaciones para la optimización de funciones no lineales, así como también al desarrollo de nuevas metodologías. En [2] se presenta una amplia discusión sobre los problemas que adolecen este tipo de técnicas para el caso particular de la estimación de modelos de redes neuronales, aunque muchas de sus conclusiones pueden ser generalizadas en el contexto general del problema de optimización. Una de las técnicas que ha gozado de bastante aceptación en la comunidad de Inteligencia Computacional para la estimación de modelos de redes neuronales es el algoritmo RPROP (Resilient Backpropagation), que es una técnica basada en el gradiente de la función de error [3, 4]. Aunque RPROP puede ser utilizado para resolver problemas de optimización multivariable no restringida, no existen referencias sobre su uso en el contexto general del problema de optimización. Más aún, esta técnica no permite el manejo de restricciones, limitando su uso en casos prácticos.

Este artículo tiene dos objetivos: primero, presentar una modificación de RPROP para incorporar el manejo de restricciones a través del uso de funciones de penalización; y segundo, introducir el algoritmo propuesto dentro de las técnicas propias de la comunidad de investigación de operaciones.

Para cumplir con los objetivos propuestos, el resto de este artículo está organizado así: en la siguiente sección se discute la versión original de RPROP; seguidamente, se introduce un esquema para el manejo de restricciones a partir de la función de penalización; posteriormente, se utilizan varias funciones benchmark para comprobar la efectividad del algoritmo propuesto; y finalmente, se concluye.

RPROP (Resilient Backpropagation)

RPROP [3, 4] es una técnica ampliamente utilizada para el entrenamiento supervisado de redes neuronales artificiales tipo perceptrón multicapa, cuyo proceso de búsqueda es guiado por la primera derivada de f(•); en este caso, f(•) es una medida de la diferencia entre la salida arrojada por la red neuronal y el valor esperado. RPROP, y su variante iRprop+ por Igel y Hüsken [5], difiere de la técnica clásica de propagación hacia atrás del error (o algoritmo backpropagation) en que las derivadas parciales de la función error sólo son usadas para determinar el sentido en que deben ser corregidos los pesos de la red pero no las magnitudes de los ajustes. Los algoritmos basados en backpropagation modifican los valores de los parámetros proporcionalmente al gradiente de la función de error, de tal forma que en regiones donde el gradiente tiende a ser plano el algoritmo avanza lentamente; esta modificación se hace a través de un único parámetro que controla la velocidad de avance del algoritmo. RPROP utiliza parámetros independientes que controlan la velocidad con que se recorre la función objetivo para cada uno de los pesos de la red neuronal. RPROP tampoco se ve afectado por la saturación de las neuronas de la red neuronal, ya que solamente se usa la derivada para determinar la dirección en la actualización de pesos. Consecuentemente, converge más rápidamente que los algoritmos basados en backpropagation.

En ésta investigación se utilizó la variante iRprop+, en la cual los parámetros de la red neuronal en la iteración k + 1 son actualizados como:

donde 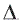w_ij es estimado con una función del cambio de signo de la derivada del error entre las iteraciones k y k-1 , y del tamaño del paso 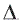tal como se realiza tradicionalmente en las técnicas basadas en el gradiente. Así, si el signo de la derivada no cambia en las dos últimas iteraciones, entonces el tamaño de paso 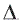es incrementado en un factor η⁺ pero limitado a que su valor máximo no supere 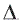_max que corresponde al tamaño máximo de la modificación de w_ij.

Cuando se presenta el cambio de signo de las derivadas el algoritmo sobrepaso el punto de mínima; consecuentemente, el tamaño de paso es reducido en un factor η^- pero limitando el tamaño mínimo de modificación de w_ij a un valor 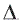_max. Si la derivada es cero no se modifica el tamaño de paso.

Función de penalización

Con el fin de aprovechar las ventajas mencionadas y el rendimiento que ofrece la técnica [6] en la optimización de perceptrones multicapa, se propone el algoritmo CONRPROP (constrained RPROP) como una adaptación del algoritmo iRprop+ que permite minimizar funciones no lineales sujetas a restricciones como las descritas en (2) y (3). Para ello es necesario que RPROPCON incorpore, además de la técnica de Rprop, una técnica de penalización para convertir el problema de optimización restringida en uno sin restricciones.

Hoffmeister y Sprave [7] proponen introducir una penalización dentro de la función objetivo f() que permita medir el grado en que las restricciones descritas por (2) y (3) son violadas. Así, RPROP debe operar sobre una nueva función F() definida como:

donde Ω representa la región factible; M_c es el máximo conocido en la región factible; y d_c es una medida de penalización de las restricciones que no se cumplen. En esta implementación, d_c se define como:

donde H_i es una variable que toma el valor de uno si la i-ésima restricción ha sido violada y cero en caso contrario; y R_i es el valor que toma g_i(x) o h_i(x) en el punto x. La versión propuesta es presentada en la figura 1.

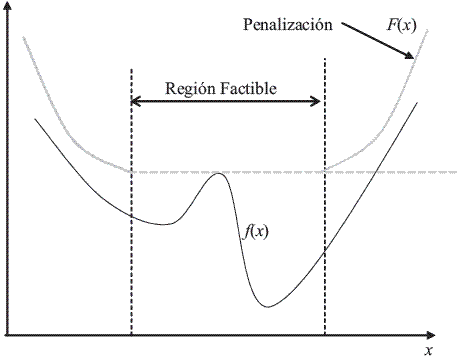
Según (5), F() es evaluada al valor máximo de f() en la frontera de la región factible causando una discontinuidad; así, cualquier punto al interior de la región factible será preferido a un punto en la frontera. Si el punto actual está por fuera de la región factible, la penalización d_c obliga a que el algoritmo se dirija hacia la región factible; una vez dentro de ella, iRprop+ opera de la forma tradicional. El efecto de la penalización es esquematizado en la figura 2,

Figura 1 Algoritmo CONRPROP

Figura 2 Efecto de la penalización en la evaluación de la función objetivo

Resultados experimentales y comparación

Para comprobar la efectividad del algoritmo CONRPROP se realizaron una serie de pruebas con los problemas de optimización presentados en la Tabla 1; cada uno de ellos presenta una relativa complejidad y han sido comúnmente usados en la literatura para la comparación de técnicas de optimización. El problema 1 posee dos restricciones: una inecuación no lineal y una ecuación lineal, fue abordado en [8]. El 2 no posee restricciones [9]; el 3 fue diseñado con un punto estacionario no óptimo en 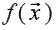≈ 8, esto puede causar una convergencia prematura [10]; en el 4 la función objetivo fue definida fuera de la región factible [11]; el 5 está sujeto a dos restricciones: una inecuación no lineal y otra lineal [8]; y el problema 6 posee 5 variables, está sujeto a 6 inecuaciones no lineales y 10 límites sobre las variables independientes, nótese que en la función objetivo los coeficientes de x₂ y x₄ son cero, es decir, x₂ y x₄ no están incluidos en la definición de .

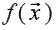En la tabla 1, se presentan los resultados experimentales obtenidos, estos muestran que el desempeño al resolver problemas de programación no lineal con CONRPROP es satisfactorio. En la mayoría de los problemas, el resultado de la optimización es mejor que el reportado por otros autores; este es el caso de los problemas 1, 5 y 6 donde el punto óptimo es menor que el reportado.

Para los problemas 2 y 3 los puntos obtenidos son iguales a los alcanzados por otras técnicas. Por otro lado, aunque para el problema 4 el óptimo logrado es mayor que el reportado, la aproximación obtenida es muy cercana. Cabe anotar que

Tabla 1 Soluciones obtenidas usando RPROPCON

Tabla 1 continuación

Conclusiones

En éste trabajo se presentan los resultados obtenidos al resolver problemas de optimización no lineal con restricciones usando una técnica propia de la optimización de redes neuronales, RPROP. Las contribuciones de este trabajo están relacionadas con los siguientes aspectos: Se propone CONRPROP como una adaptación y generalización de la técnica de RPROP, incorporando una función de penalización para resolver problemas de optimización no lineal. Dados los resultados presentados, se comprobó experimentalmente que la efectividad de RPROPCON al resolver problemas de programación no lineal es satisfactoria.

Agradecimientos

Los autores agradecen a los evaluadores anónimos cuyos comentarios permitieron mejorar la calidad de este artículo.

Referencias

1, P. M. Pardalos, M. G. C. Resende. Handbook of Applied Optimization. Ed. Oxford University Press. New York. 2002. pp. 263-299.        [ Links ]

2, Y. LeCun, L. Bottou, B. Orr, K. R. Muller. "Efficient Backprop". Neural Networks - Tricks of the Trade, Springer Lecture Notes in Computer Sciences. Vol. 1524. 1998. pp. 5-50.        [ Links ]

3. M. Riedmiller, H. Braun. "A direct adaptive method for faster backpropagation learning: The RPROP algorithm". Proceedings of the IEEE International Conference on Neural Networks. San Francisco (CA). 1993. pp. 586-591.        [ Links ]

4. M. Riedmiller. "Advanced supervised learning in multi-layer perceptrons - from backpropagation to adaptive learning algorithms". Computer Standards and Interfaces. Vol. 16. 1994. pp. 265-278.        [ Links ]

5. C. Igel, M. Hüsken. "Improving the Rprop learning algorithm". Proceedings of the Second International Symposium on Neural Computation, NC2000, ICSC Academic Press. Berlín. pp. 115-121.        [ Links ]

6. D. Ortíz, F. Villa, J. Velásquez. "A Comparison between Evolutionary Strategies and RPROP for Estimating Neural Networks". Avances en Sistemas e Informática. Vol.4. 2007. pp. 135-144.        [ Links ]

7. F. Hoffmeister, J. Sprave. "Problem-independent handling of constraints by use of metric penalty functions". L. J. Fogel, P. J. Angeline, T. Bäck (Editores). Proceedings of the Fofth Annaul Conference on Evolutionary Programming. (EP'96). San Diego (CA). MIT press. 1996. pp. 289-294.        [ Links ]

8. J. Bracken, G. McCormick. Selected Applications of Nonlinear Programming. Ed. Jhon Wiley & Sons. Inc. New York. 1968. pp. 16.        [ Links ]

9. H. Rosenbrock. "An Automatic Method for Finding the Greatest and Least value of a Function". Computer Journal. Vol. 3. 1960. pp. 175-184.        [ Links ]

10. A. R. Colville. A comparative study on nonlinear programming codes. IBM Scientific Center Report No. 320-2949. New York. 1968. pp. 12.        [ Links ]

11. D. Paviani. A new method for the solution of the general nonlinear programming problem. Ph.D. dissertation. The University of Texas. Austin. Texas. 1969. pp. 18.        [ Links ]

(Recibido el 14 de diciembre de 2007. Aceptado el 24 de agosto de 2009)

^*Autor de correspondencia. teléfono: + 57 + 4 + 425 53 70, correo electrónico: jdvelasq@unal.edu.co (J. Velásquez)