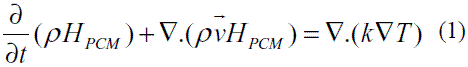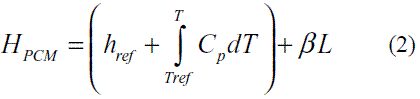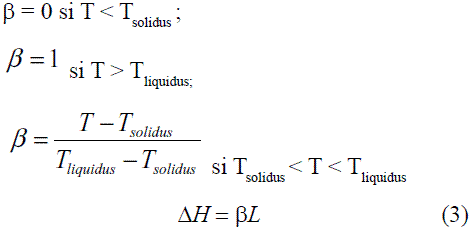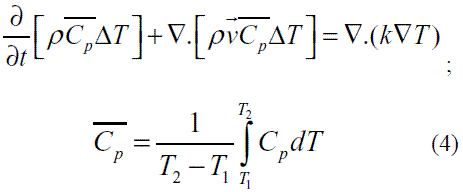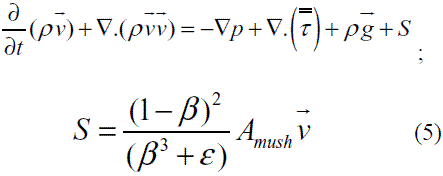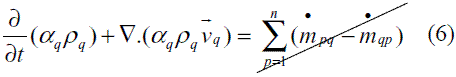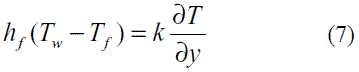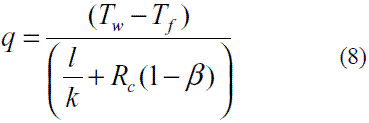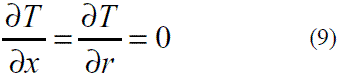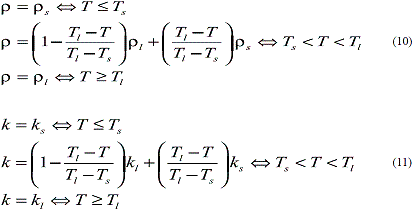Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230On-line version ISSN 2422-2844
Rev.fac.ing.univ. Antioquia no.51 Medellín Jan./March 2010
Análisis de un sistema de almacenamiento de energía térmica usando cloruro de magnesio hexahidratado
Analysis of a system of storage heat thermal using magnesium chloride hexahydrate
Andrés Felipe Macía , Jhon Camilo Parra, Farid Chejne
Grupo de Termodinámica Aplicada y Energías Alternativas (TAYEA), Facultad de Minas Universidad Nacional de Colombia- Sede Medellín, Cra. 80 No 65-223, Medellín, Colombia
Resumen
Se simuló el comportamiento del cloruro de magnesio hexahidratado (MgCl2*6H2O) como almacenador de energía térmica, que posee una temperatura de transición de fase de 117oC; lo que lo convierte en un material con gran potencial en el área de las aplicaciones de mediana temperatura (aplicaciones industriales). Se desarrolló una simulación CFD usando el software FLUENT para describir la fusión/solidificación de la sal hidratada. Se observó el efecto del uso de aletas y las fuerzas boyantes producidas por los efectos gravitacionales.
Palabras clave: Almacenamiento de energía, materiales con cambio de fase(PCM), Fluent, sales hidratadas
Abstract
It was analyzed the behavior of hexahydrate magnesium chloride (MgCl2*6H2O) as a thermal energy storage, which has a phase transition temperature of 117oC and is becoming a material with great potential in the application of medium temperature (industrial applications). It was developed a simulation using the CFD software FLUENT to describe the melting/solidification of the hydrated salt. It was observed the effect of the use of fins and buoyant forces produced by gravitational effects.
Keywords: Storage Energy, phase change materials (PCM), Fluent, salts hydrates
Introducción
La importancia del uso racional de la energía y la protección del medio ambiente han incrementado el interés por la investigación en energías renovables y en la forma de almacenar energía de fuentes emisivas. El almacenamiento de la energía solar en forma de calor latente es una alternativa para el óptimo aprovechamiento de este recurso.
Estos sistemas usan materiales que cambian de fase conocidos como PCM (Phase Change Material). En los últimos años se ha realizado un gran número de estudios teóricos y experimentales para modelar el problema del cambio de fase, observar el desempeño térmico de las unidades de almacenamiento, investigar el potencial de nuevas geometrías y proponer unidades modulares para aplicaciones residenciales y comerciales [1].
Los materiales usados como Materiales con Cambio de Fase (PCM) para el almacenamiento de energía térmica en forma de calor latente deben tener las siguientes características: Alto valor del calor latente, alta conductividad térmica, una temperatura de fusión práctica de operación, ser químicamente estables, fundir congruentemente con mínimo subenfriamiento, de bajo costo, no tóxicas y no corrosivas [2]. Este tipo de materiales se clasifican en dos grupos: orgánicos e inorgánicos.
Entre los materiales orgánicos se destacan las parafinas las cuales tiene un elevado calor de fusión por unidad de peso, no son tóxicas ni corrosivas, son químicamente estables e inertes por debajo de 500oC. Sus principales desventajas son: tienen una baja conductividad térmica y son inflamables. [3-5]. Entre los materiales inorgánicos se destacan las sales hidratadas y otros compuestos orgánicos. Varios autores [2] han sugerido el uso de agentes nucleantes y de crecimiento para aminorar estos problemas de segregación y subenfriamiento.
Los PCM poseen bajas conductividades que dificultan la transferencia de calor y por lo tanto necesitan mejorarse mediante técnicas especiales; como el uso de aletas, de matrices de sostén que consiste en crear una matriz o estructura soporte de un material con alta conductividad térmica en el cual se deposita el PCM; etc. [6-9]. La ventaja adicional del almacenamiento de calor latente es que el almacenamiento de la energía y la entrega ocurren normalmente sobre un intervalo de temperatura bastante estrecha (la zona de transición de la fase) [10].
El objetivo de este trabajo es analizar un sistema de almacenamiento de energía térmica mediante cambio de fase usando el MgCl2 6H2O evaluando diferentes características como la influencia de las aletas y la temperatura de entrada del fluido de intercambio de calor (HTF) en la cantidad de material fundido, además se hace un análisis del modelo al considerar las fuerzas boyantes durante el proceso de fusión.
Modelo matemático
El modelo matemático bidimensional en estado no estacionario, fue solucionado con la herramienta numérica FLUENT versión 6.2, el cual aplica el método entalpía-porosidad y está constituido por balances de momentum y energía. Para el fluido de transferencia de calor se trabajó con aceite térmico bajo condiciones de flujo turbulento y se realizaron simulaciones utilizando el modelo de turbulencia k-ε estándar.
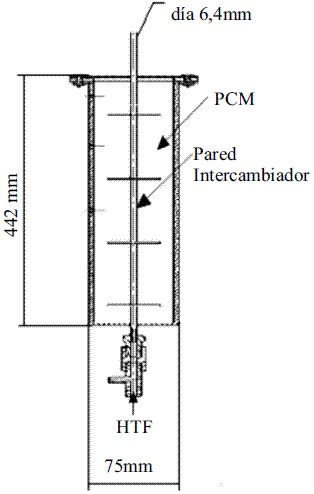
Un esquema ilustrativo del sistema de almacenamiento de energía térmica analizado se presenta en la figura 1, el cual está conformado por dos tubos concéntricos. Por el tubo interior circula el fluido de transferencia de calor (HTF, Heat Transfer Fluid) que para el caso propuesto fue aceite térmico, en flujo turbulento para lo que se usó el modelo de turbulencia k-ε, En el espacio anular entre los dos tubos se ubica el material con cambio de fase (PCM, Phase Change Material) que en este trabajo corresponde a MgCl2*6H2O.
Durante el proceso de carga el fluido de transferencia de calor calienta al PCM hasta que el se funda totalmente almacenando la energía. Durante el proceso de descarga el PCM se solidifica y el calor almacenado es liberado al fluido frío.
El modelo matemático formulado utiliza el método de la entalpía-porosidad implementado en el paquete comercial FLUENT® para modelar el proceso de solidificación/fusión. En este la interfase fundida no se obtiene de forma explícita. En cambio se considera una cantidad llamada fracción líquida, que indica la fracción de volumen en forma líquida que está asociado con cada celda del volumen de control. La fracción líquida es calculada en cada iteración, sobre el balance de entalpía [11].
Figura 1 Esquema del sistema de almacenamiento de energía
Para la formulación del modelo matemático se tuvieron en cuenta las siguientes suposiciones:
El PCM es isotrópico y homogéneo.
El fluido de transferencia de calor (HTF) se considera incompresible y newtoniano.
La velocidad y temperatura de entrada del HTF son constantes.
La temperatura inicial del sistema de almacenamiento de energía es uniforme y el PCM se encuentra en la fase sólida para el proceso de fusión.
En el PCM, en el fluido de transferencia de calor y en las paredes del tubo las variaciones de temperatura en la dirección angular son asumidas despreciables.
El problema se considera axisimétrico respecto al eje vertical.
Las propiedades termofísica del fluido de transferencia de calor, las paredes del tubo y el PCM se consideran constantes.
Balance de energía
El balance de energía para el material con cambio de fase (PCM) es:
k = Conductividad Térmica del PCM
ρ = Densidad del PCM
v = Velocidad del PCM
Para el balance de energía sobre el PCM, MgCl2*6H2O, la entalpía se presenta en la ecuación (2) y es la contribución del calor sensible y el calor latente (L).
href = Entalpía de referencia
Tref = Temperatura de referencia
Cp = Calor específico
L = Calor latente de fusión
La fracción líquida (β) se define como [11].
El balance de energía para el aceite térmico es:
Balance de momentum para el MgCl2*6H2O
El método de entalpía-porosidad trata la interfase fundida como un medio poroso. En este caso la porosidad será igual a la fracción líquida β. Para la región sólida, la porosidad es igual a cero y las velocidades son nulas para esta región. Amush corresponde a una constante que caracteriza esta región; puede tomar valores entre 104 y 106; ε corresponde a un número muy pequeño (0,001) para evitar las divisiones por cero. Este término fuente al igual que los términos del gradiente de velocidad deben estar presentes ya que existe una velocidad relativa entre el material fundido y el sólido [11].
Modelo de turbulencia para el aceite térmico
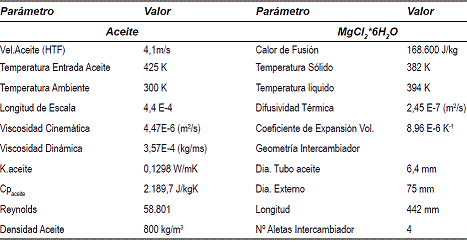
Debido a las condiciones de flujo correspondientes a un Reynolds de 58.800 (Tabla 1) se considera flujo turbulento y para representarlo se utilizará un modelo k-ε. semi-empírico con base en modelos de la ecuación de transporte de la energía cinética de turbulencia (k) y la rata de disipación (ε). [11], [12].
Modelo multifase
Debido a la geometría del sistema de almacenamiento que se va a modelar (Figura 1), es necesario considerar los dos fluidos (Aceite y PCM) de forma simultánea. Se requiere un modelo que permita diferenciar cuál fluido cambia de fase y cuál es el fluido que solo está transfiriendo energía. [12]. En la ecuación (6) se presenta la fracción de volumen de la interfase y se obtiene a partir de la ecuación de continuidad para la fase q:
Donde 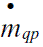 es la transferencia de masa de la fase q a la fase p y
es la transferencia de masa de la fase q a la fase p y 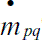 es la transferencia de masa de la fase p a la q, pero como en el modelo propuesto no hay transferencia de masa entre las fases o los fluidos, entonces el lado derecho de la ecuación será igual a cero.
es la transferencia de masa de la fase p a la q, pero como en el modelo propuesto no hay transferencia de masa entre las fases o los fluidos, entonces el lado derecho de la ecuación será igual a cero.
Condiciones de frontera
Entrada del aceite X =0; v = cte v= velocidad del fluido.
Salida del aceite X= L; Ps = Patm
Ps: Presión a la salida del sistema de almacenamiento
Patm: Presión atmosférica
Entre el aceite y la pared del intercambiador 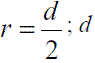 = diámetro del intercambiador.
= diámetro del intercambiador.
hf = Coeficiente local de transferencia de calor del aceite.
Tw = Temperatura de Pared.
Tf = Temperatura local del fluido.
k = conductividad térmica de la pared
Entre la pared del intercambiador y PCM R = R pp
l = distancia entre la pared y el centro de la celda cercana a la pared
k = Conductividad térmica del PCM
Rc = Resistencia térmica de contacto entre la pared y el PCM
T = Temperatura en el centro de la celda
Paredes externas del PCM
Ecuaciones constitutivas
En el modelo se considera la variación de la densidad y la conductividad térmica con el cambio de fase del MgCl2*6H2O, en las ecuaciones (10) y (11) se definen estas propiedades respectivamente.
Donde:
ρ= densidad del PCM
ρs = 1569 kg/m3 densidad en estado sólido del PCM
ρl = 1450 kg/m3 densidad en estado líquido del PCM
k = conductividad térmica del PCM
ks = 0,694 W/mK conductividad en estado sólido del PCM
kl = 0,57 W/mK conductividad en estado líquido del PCM
Ts = 382 K Temperatura de solidus
Tl = 394 K Temperatura de liquidus
Resultados
En esta sección se presentan los resultados de simulación obtenidos para el proceso de fusión del MgCl2*6H2O. En la tabla 1 se presentan los parámetros de la simulación que fueron seleccionados a partir de un trabajo experimental realizado con anterioridad y que permitiera la validación de los resultados obtenidos con el modelo [12].
Comparación entre sistema con aletas y sin aletas
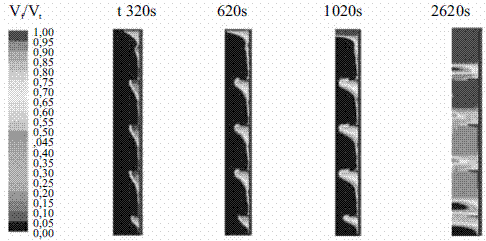
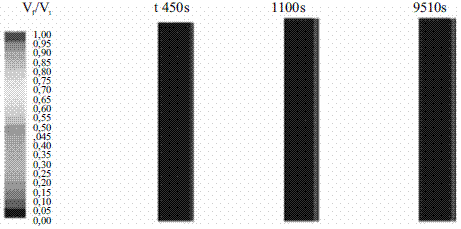
En la figura 2 se presentan las simulaciones realizadas al sistema de almacenamiento utilizando intercambiador liso y con aletas considerando las fuerzas gravitacionales, para observar su influencia sobre la fracción fundida (Vf/VT) definida como la relación entre el volumen en estado líquido (Vf) y el volumen total (VT) de PCM. En esta figura se observa que para las condiciones de operación con la que se simuló el HTF (temperatura de 425K, y un flujo de 1,28 x 10-4 m3/s), el intercambiador liso no logra transferir la energía necesaria para que el MgCl2*6H2O cambie de fase, mientras que utilizando 4 aletas distribuidas longitudinalmente sobre el intercambiador de calor, se obtiene una fracción fundida del 95% luego de 45 minutos (2.620 s) de operación, mostrando la importancia de utilizar sistema aleteado para este tipo de PCM.
Tabla 1 Parámetros de simulación para la fusión
Figura 2a Fracción fundida para un intercambiador con aletas
Figura 2b Fracción fundida para un intercambiador liso
Influencia de la fuerza gravitacional
En la figura 3 se presenta la comparación de la fracción fundida del MgCl2*6H2O cuando se consideran (en el sentido de la flecha) y desprecian las fuerza gravitacional durante el proceso de fusión.
En la figura 3 se puede observar la importancia de tener presente los efectos de las fuerzas de flotación cuando se pretende modelar el fenómeno de fusión de un material en este tipo de sistemas de almacenamiento. Realizando una comparación cuantitativa, el efecto de las fuerzas de flotación genera una reducción de casi una décima parte del tiempo de fusión cuando no se desprecia la gravedad.
También se puede observar en la figura 3 que la transferencia de calor entre el intercambiador y el PCM toma casi el doble del tiempo cuando no se considera el efecto de la fuerza gravitacional, la principal causa por la que ocurre este fenómeno es debido a las fuerzas de flotación que se generan por la diferencia de densidad entre el estado sólido y líquido del MgCl2*6H2O, causando que la transferencia de calor no sea solo por conducción al interior del sistema que ocurre cuando no se tiene presente la fuerza gravitacional, sino que también producen unos altos gradientes de temperatura debido al material fundido que asciende en convección libre, transfiriendo una mayor cantidad de energía.
Figura 3a Fracción líquida Taceite 425K con g = 9,81m/s2
Figura 3b Fracción líquida Taceite 425K con g = 0 m/s2
Influencia de la temperatura del aceite
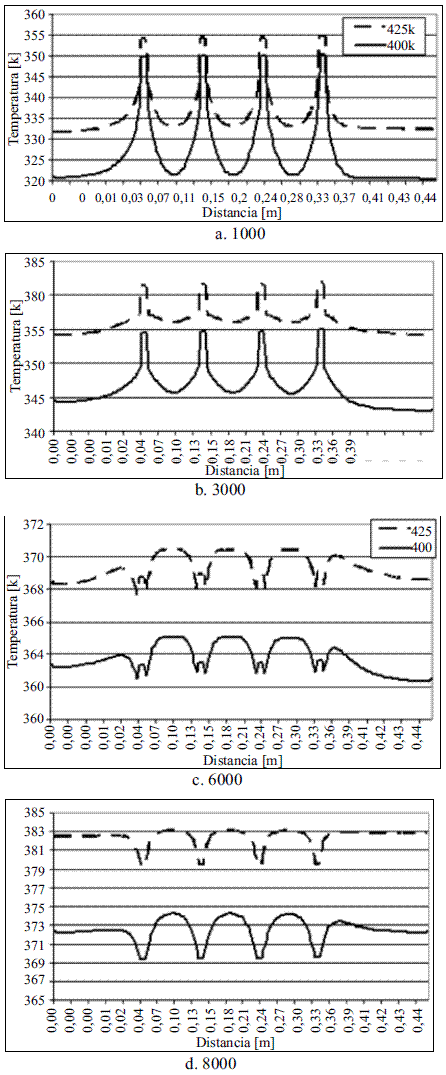
En la figura 4 se presentan los perfiles de temperatura al interior del MgCl2*6H2O para una posición radial constante de 2,6 cm respecto a la pared del intercambiador. Las simulaciones se realizaron para temperaturas de entrada del aceite de 425 y 400 K.
En la figura 4 se observa que la diferencia de 25 K entre la temperatura del aceite, causa un incremento de 10 K al interior del PCM y se mantiene constante durante el proceso de fusión, mostrando una influencia directa en el desempeño del sistema de almacenamiento.
Figura 4 Perfil de temperatura del MgCl2*6H2O para dos temperaturas de entrada del aceite
En las figuras 4a y 4b se observa que entre los 1.000 y 3.000 segundos de calentamiento en área cercana a las aletas se presentan gradientes de temperatura mayores a 20 K durante el calentamiento por calor sensible en todo el sistema, sin depender de la temperatura de entrada del aceite.
Como se ilustra en las figuras 4c y 4d entre los 6.000 y 8.000 segundos de calentamiento las temperaturas más bajas están en el área donde se encuentran las aletas, que es totalmente diferente de lo que ocurría durante los primeros segundos. La principal causa que genera este comportamiento es que ya hay presencia de material fundido generando un cambio en el mecanismo de transferencia de calor, ya que antes era solo por conducción pero luego de fundirse comienza la transferencia por convección. Además, por el cambio de fase hay una mayor energía.
Validación del modelo
Para la validación del modelo se usaron los resultados experimentales obtenidos por Macia [12], y se realizaron dos tipos de simulaciones: En una simulación se consideró que la densidad y la conductividad térmica del PCM dependían de la temperatura y se definían según las ecuaciones (10) y (11). La otra simulación se consideró que las propiedades del PCM son constantes durante todo el proceso de calentamiento.
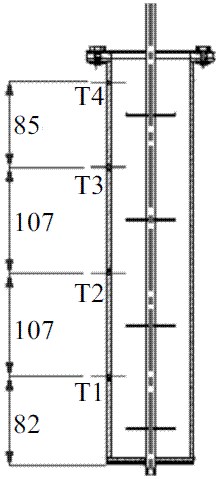
En la figura 5 se muestran los puntos de medición de temperatura durante las pruebas experimentales.
Figura 5 Puntos de medida de temperatura
En la figura 6 se presentan los resultados teóricos y experimentales en los cuatro puntos diferentes del intercambiador definidos anteriormente.
De los resultados exhibidos en la figura 6 se observa que a lo largo del intercambiador hay dos zonas que tienen un desempeño diferente durante el proceso de fusión. La región 1 que comprende los puntos de medición T1 y T2 se observa a partir de las simulaciones realizadas y los datos experimentales el principal mecanismo de transferencia de calor es por conducción y está de acuerdo con lo reportado [13]. El promedio del los errores relativos para las simulaciones con propiedades constantes es de 13,6 y 6,8% para T1 y T2, respectivamente; mientras que para las simulaciones con propiedades variables el promedio de los errores relativos es de 16,3 y 11,9% que demuestra la mejor aplicación de la simulación con propiedades constates para la zona donde la transferencia de calor es por conducción. La región 2 que comprende los puntos de medición T3 y T4 se observa que a partir de las simulaciones realizadas y los datos experimentales la transferencia de calor ya es una combinación entre conducción y convección, y el promedio del los errores relativos para las simulaciones con propiedades constantes es de 13,7 y 8,3% para T3 y T4 respectivamente mientras que para las simulaciones con propiedades variables el promedio de los errores relativos es de 7,3 y 9,4% que demuestra la mejor aplicación de la simulación con propiedades variables para esta zona.
En la figura 6 se observa además que en los 4 puntos de medición durante el inicio del proceso cuando el material se encuentra en estado sólido las simulaciones con propiedades constantes tienen una mayor velocidad de calentamiento que los resultados experimentales y las simulaciones con propiedades variables, el motivo por la que esto sucede es que para las simulaciones con propiedades constantes se consideraron las propiedades del PCM de la fase líquida y la densidad del PCM en estado líquido es un 10% menor respecto al estado sólido y por ende habrá una menor masa por calentar para el mismo volumen.
Figura 6 Validación del modelo teórico con resultados experimentales
Conclusiones
Se utilizó la plataforma de FLUENT 6.2 para simular de forma acoplada el fluido de transferencia de calor (HTF) y el MgCl2*6H2O, que es una innovación ya que todos los modelos parten de una pared caliente y no tienen en cuenta las condiciones de flujo.
Para la simulación se utilizó un modelo de solidificación/fusión, modelo multifases y el modelo de turbulencia permitiendo obtener resultados muy importantes sobre el efecto de la fuerza gravitacional y los cambios de la densidad en la fusión del material.
Usando aletas en el intercambiador se logra fundir el 95% del PCM en 45 minutos, mientras que en el intercambiador liso al cabo de 2,5 horas no se ha obtenido ni un 5% de material fundido, demostrando la necesidad de usarlas para este tipo de aplicaciones.
Los errores relativos del modelo respecto a los resultados teóricos son menores al 17% que son unos resultados muy buenos, y demuestran la posibilidad de usar este modelo para el diseño y simulación de sistemas de almacenamiento de energía mediante cambio de fase.
Agradecimientos
A la Dirección Nacional de Investigaciones de la Universidad Nacional de Colombia por el apoyo brindado al proyecto: Almacenamiento de Energía Solar Térmica usando Cloruro de Magnesio Hexahidratado.
Referencias
1. K. A. R. Ismail, M. M. Gonçalves. Thermal Performance of a PCM Storage Unit, Energy Conversion & Management. Vol. 40. 1999. pp. 115- 138. [ Links ]
2. M. M. Farid, A.M. Khudhair, S.A.K. Razack, S. Al- Hallaj. A Review on Phase Change Energy Storage: Materials And Applications. Energy Conversion and Management. Vol 45. 2004. pp. 1597-1615. [ Links ]
3. B. He, V. Martin, F. Setterwall. Liquid-Solid Phase Equilibrium Study of Tetradecane And Hexadecane Binary Mixtures As Phase Change Materials (Pcms) For Comfort Cooling Storage. Fluid Phase Equilibria. Vol. 212. 2003. pp. 97-109. [ Links ]
4. A. Sari, K. Kaygusuz. Thermal Performance of Myristic Acid as A Phase Change Material for Energy Storage Application. Renewable Energy. Vol. 24. 2001. pp. 303-317. [ Links ]
5. A. Sari, K. Kaygusuz. Thermal Energy Storage System Using Stearic Acid As A Phase Change Material.Solar Energy. Vol. 71. 2001. pp. 365-376. [ Links ]
6. F. Frusteri, V. Leonardi, G. Maggio. Numerical Approach to Describe the Phase Change Of An Inorganic PCM Containing Carbon Fibres. Applied Thermal Engineering. Vol. 26. 2006. pp. 1883-1892. [ Links ]
7. K. A. R Ismail, J. R. Henríquez, L. F. M Moura, M. M. Ganzarolli. Ice Formation Around Isothermal Radial Finned Tubes. Energy Conversion & Management. Vol. 41. 2000. pp. 585-605. [ Links ]
8. V. R. Voller. Numerical Treatment of Rapidly Changing and Discontinuos Conductivities. Int. J. of Heat and Mass Transfer. Vol. 44. 2001. pp. 4453- 4556. [ Links ]
9. J. Fukai, Y. Hamada, Y. Morozumi, O. Miyatake. Effect of Carbon-Fiber Brushes on Conductive Heat Transfer in Phase Change Caterials. Int. J. of Heat and Mass Transfer. Vol. 45.2002. pp. 4781-4792. [ Links ]
10. S. M Hasnain. Review on Sustainable Thermal Energy Storage, Part I: Heat Storage Materials and Techniques. Energy Conversion Managers. Vol. 39. 1998. pp. 1127-1138. [ Links ]
11. Fluent® 6.2 User's Guide. Graphics Version 6.2. Fluent Inc. 2005.
12. A. F. Macía. Almacenamiento de Energía Solar Térmica Usando Cloruro de Magnesio Hexahidratado. Tesis de Maestría. Universidad Nacional de Colombia. Medellín. 2007. pp. 28-65. [ Links ]
13. A. F. Regin, S. C. Solanki, J. S. Saini. Latent heat thermal energy storage using cylindrical capsule: Numerical and experimental investigations Renewable Energy. Vol. 31. 2006. pp. 2025-2041. [ Links ]
*Autor de correspondencia: teléfono: + 57 + 4 + 425 53 33, fax + 57 + 4 + 230 5351, correo electrónico: afmacia@unal.edu.co (A. Macía).