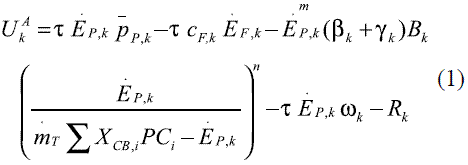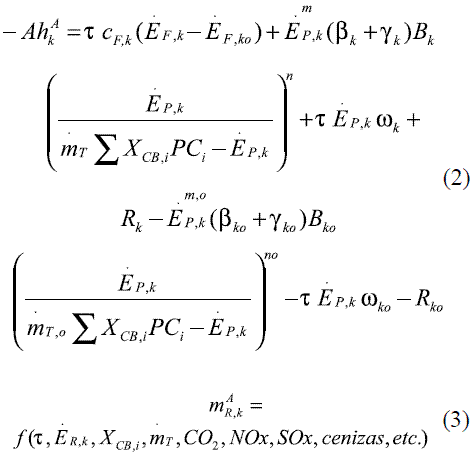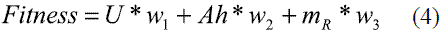Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230On-line version ISSN 2422-2844
Rev.fac.ing.univ. Antioquia no.51 Medellín Jan./March 2010
Análisis multiobjetivo a un sistema energético
Multiobjective analysis to an energy system
Marlon Bastidas1, Patricia Jaramillo1, Farid Chejne1, Blas Galván2
1Universidad Nacional de Colombia sede Medellín, Cra 80 No 65 -223, Medellín, Colombia
2Universidad de las Palmas de Gran Canaria, Juan de Quesada, No 30 Las Palmas de Gran Canaria -35001-España.
Resumen
Se presenta una metodología reciente para optimización de un sistema energético complejo introduciendo factores externos, basada en el desarrollo de fronteras Pareto -óptimas a partir de algoritmos evolutivos multiobjetivos (AEMO) empleados en la resolución de problemas energéticos reales de optimización no lineal. Se incluyen objetivos: termo-económico, tecnológico y ambiental, a los cuales se les asigna un peso para evaluar la función de aptitud, formada por una suma de promedios de cada objetivo. El sistema energético complejo está formado por un ciclo combinado (subsistema I) y un gasificador (subsistema II).
El desempeño de los pesos en cada objetivo se modela por reglas heurísticas, mientras que las modificaciones de las variables de decisión se basan en aplicaciones aleatorias. La metodología expuesta, permite evaluar funciones objetivo formadas por costos del combustible, costos variables de operación y costos de mantenimiento, los cuales están incluidos en la ecuación de capital de inversión. Las metas en la optimización del sistema global son minimizar los costos del producto, minimizar los residuos de la combustión y maximizar la eficiencia exergética.
Palabras clave: Multiobjetivo, optimización, termoeconomía
Abstract
An optimization methodology for complex energy system introducing external factors based on the newly developed Pareto-based multiobjective evolutionary algorithms (MOEA) used for solving a real-world power systems multiobjective nonlinear optimization problem is presented. The thermoeconomic, technology and environment objectives are included in this methodology and weights are assigned to each objective for evaluating the fitness and average sum. The complex energy system is integrated by a combined-cycle power plant (subsystem I) and a gasifier (subsystem II).
The performance at weights of each objective is modeled by heuristic rules whereas the modification of decision variables is based on the application of random approaches. The methodology allows evaluating objective functions conformed by the fuel costs, the operation variable costs and maintenance costs. These are included in the capital investment equation. The goals in the optimization of this global system are to minimize product costs, minimize combustion residuals and maximize exergetic efficiency.
Keywords: Multiobjective, optimization, thermoeconomic
Introducción
Los desarrollos teóricos de optimización de sistemas energéticos en los últimos años están demarcados en la exergoeconomía, teniendo en cuenta que los análisis relacionados con los costos económicos de generación exergética, son más apropiados para un caso real que los obtenidos de un simple análisis energético [1]. El término compuesto Termoeconomía, propuesto por Evans y Tribus en 1962, tiene como propósito esencial estudiar la relación entre la termodinámica y la economía, mencionar las bases teóricas de una nueva disciplina de ahorro energético y obtener modelos que permitan recoger criterios generales para evaluar la eficiencia y el costo de sus productos, en sistemas con un consumo intensivo de energía. En los noventa se presentaron trabajos con una metodología termoeconómica bien argumentada, que favoreció su reconocimiento científico [2, 3].
La teoría termoeconómica, propició la presentación de nuevos trabajos y se desarrollaron diferentes aplicaciones a partir de ésta. Una vez se comprobara que la teoría termoeconómica permitiera resultados razonables, empezó a aplicarse en diferentes tipos de tecnologías de generación energética; especialmente al sistema general - CGAM [1, 4, 5]. Hasta ahora, se han implementado herramientas de optimización en los sistemas de generación de energía (SGE), a partir de conceptos que provienen de la termodinámica y la economía; sin embargo, consideramos que el análisis MO puede complementar la optimización, dado que permite incluir variables del entorno a un sistema energético complejo [6, 7].
A nivel exergoeconómico, en los últimos 25 años se han desarrollados metodologías de contabilidad de costos que optimizan y evalúan los sistemas con un enfoque de costo promedio o ejemplificando con costos marginales [1, 8]. Se ha intentado plantear metodologías MO, para la optimización de sistemas energéticos, pero siempre conducen a óptimos locales, sin embargo se han hecho planteamientos que muestran la necesidad de utilizar varios criterios de evaluación para la escogencia de un sistema energético óptimo entre varias posibilidades [9-10]. Con este trabajo, se logra mostrar la importancia de incluir factores externos en la optimización de un sistema energético, dada la influencia por el criterio del decisor, la posibilidad de confrontar puntos óptimos y la deducción de ecuaciones para el análisis MO [10, 11].
Descripción del problema térmico multiobjetivo (MO)
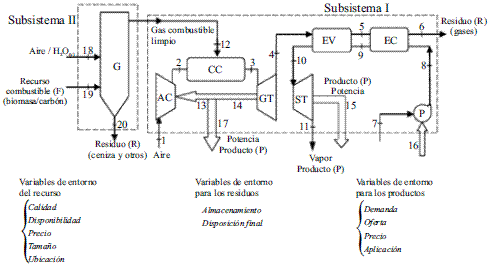
Para describir el problema MO se parte de un sistema, tal como se muestra en la figura 1. Este sistema está formado por un subsistema I, planteado por P.K. Sahoo para su aplicación metodológica, que genera 50 MW y 15 lb/s de vapor saturado a 22,5 psig [1]. El subsistema II, es un gasificador que suministra de gas sintético al subsistema I. En este caso se hace una modificación al sistema de Sahoo, el cual emplea como recurso gas natural, reemplazado en este caso por el gas sintético obtenido, procurando mantener las propiedades exergéticas del gas natural, de tal manera que los recursos empleados sean equivalentes. Para subsistema II, se tomaron datos del documento Gasification Alternatives for Industrial Applications, del departamento de energía de EU [12].
Figura 1 Planta de cogeneración (Subsistema I) integrada a un gasificador (Subsistema II)
Si se analiza en la parte inferior de la figura 1, se puede notar que se incluyen aspectos relacionados con las variables del entorno del sistema, esto con el fin de evaluar las condiciones del medio que afectan los recursos, los productos y los residuos, y a su vez evaluar cómo afectan estos al sistema de manera global. Por ejemplo, para el caso que el recurso sea carbón, habrá factores que condicionan el suministro, tales como la calidad, la disponibilidad, el precio, el tamaño y la ubicación del proveedor.
Descripción de los objetivos en el problema MO
Los objetivos termoeconómico, tecnológico y ambiental, integrados por las ecuaciones 1, 2 y 3, se generan por el interés que tiene el decisor de evaluar las ventajas y desventajas que presenta un sistema energético; estos objetivos se pueden representar de manera general, así:
El superíndice A en cada ecuación, indica que la evaluación se hace nivelando todos los conceptos de ingresos y costos a un año; τes el tiempo en horas en un año de operación y el subíndice o mostrado en el objetivo tecnológico, indica la inclusión de un equipo de eficiencia menor (tecnología convencional - TC), requerido como referencia para compararla con la del equipo o sistema a evaluar (tecnología mejorada - TM). El signo negativo en el objetivo tecnológico, indica que los valores de costos totales para el equipo o sistema de menor tecnología, son supuestamente mayores al evaluado, de esta manera se puede reflejar un ahorro positivo en los resultados; sin embargo, en la evaluación utilizando datos del trabajo planteado por Sahoo integrado con el gasificador, de mejor eficiencia exegética que el sistema de cogeneración, en ocasiones no reflejaba este comportamiento supuesto. El objetivo ambiental, corresponde a la masa total de residuos, generados en un año de operación. El tiempo de vida útil del sistema, según Sahoo, es de 20 años, por lo tanto los costos de inversión son anualizados a una tasa de 10% [1].
El primer factor del término de la derecha de la función objetivo termoeconómica, corresponde a los ingresos obtenidos en un año de operación, en este término, se incluye el precio exergético unitario del producto 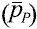 , el cual se estima como un promedio, debido a que se pueden presentar productos de diferentes calidades (vapor y electricidad), como ocurre en un sistema de cogeneración. En los factores restantes de la ecuación, se presentan los costos generados por el combustible o recurso, el cual incluye el costo exergético unitario del recurso (cF); los costos generados por la inversión en función de los costos de operación y mantenimiento constantes (β, Υ); los costos de operación y mantenimiento variables (ω) y otros costos (R) [3]. En los costos de inversión en equipos y de operación y mantenimiento, están incluidos los generados por los equipos de limpieza y de captura de CO2 [12, 13]. Las variables de funcionamiento del sistema están formadas por la exergía del recurso (EF), la exergía del producto (EP), la masa total de recurso (mT), las fracciones (XCB)y el poder calorífico (PC) de la mezcla de diferentes combustibles (i); los parámetros m, n y B son obtenidas de la ecuación de distribución de los costos de inversión [3] y k, para el caso estudiado, es el sistema energético completo, pero puede representar cada equipo que conforman el sistema.
, el cual se estima como un promedio, debido a que se pueden presentar productos de diferentes calidades (vapor y electricidad), como ocurre en un sistema de cogeneración. En los factores restantes de la ecuación, se presentan los costos generados por el combustible o recurso, el cual incluye el costo exergético unitario del recurso (cF); los costos generados por la inversión en función de los costos de operación y mantenimiento constantes (β, Υ); los costos de operación y mantenimiento variables (ω) y otros costos (R) [3]. En los costos de inversión en equipos y de operación y mantenimiento, están incluidos los generados por los equipos de limpieza y de captura de CO2 [12, 13]. Las variables de funcionamiento del sistema están formadas por la exergía del recurso (EF), la exergía del producto (EP), la masa total de recurso (mT), las fracciones (XCB)y el poder calorífico (PC) de la mezcla de diferentes combustibles (i); los parámetros m, n y B son obtenidas de la ecuación de distribución de los costos de inversión [3] y k, para el caso estudiado, es el sistema energético completo, pero puede representar cada equipo que conforman el sistema.
Aplicación de las ecuaciones del análisis MO al sistema integrado
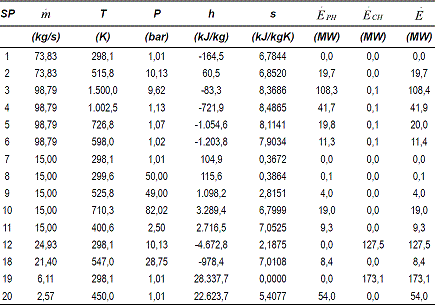
Antes de evaluar el comportamiento de los objetivos para el sistema energético, se hace el correspondiente análisis exergético del subsistema II, teniendo en cuenta que el subsistema I ha sido ampliamente evaluado por varios autores [1], para este caso se toman los datos del problema resuelto por Sahoo del subsistema I, y algunas referencias para obtener los valores necesarios para el subsistema II [12]. Los valores del análisis exergético del subsistema II, se muestran en la tabla 1, que complementan los obtenidos por Sahoo en el subsistema I. En la tabla 1, las columnas identifican las propiedades termodinámicas de cada corriente (SP) del sistema, el flujo másico (m), la temperatura T, la presión P, la entalpía h, la entropía s, la exergía física EPH, la exergía química ECH y la exergía total E.
Tabla 1 Propiedades de estado y exergía del sistema correspondiente a la figura 1
Las ecuaciones para el análisis MO, requieren de varios parámetros consignados en la tabla 2. Los valores de β, Υ, βo y Υo, se tomaron del ejemplo planteado por Tsatsaronis y Pisa [4]; los valores de ω, ωo, R y Ro, fueron asumidos inicialmente y posteriormente evaluados para diferentes cambios en las variables; los valores de B, Bo, m, mo, n y no se evaluaron para dos condiciones de operación del sistema integrado, aplicando un algoritmo de búsqueda y las recomendaciones de Bejan et al. [3].
El análisis consiste en evaluar el comportamiento de las ecuaciones con respecto a algunas variables, considerando lo siguiente:
El gas natural de la corriente 12 de la figura 1, en el análisis de Sahoo, es reemplazado por gas sintético obtenido del gasificador (subsistema II).
La cantidad de exergía de la corriente 12, permanece constante e igual a la aportada por el gas natural, los otros flujos de la misma corriente y de las corrientes 18, 19 y 20 dependen del flujo de exergía de la corriente 12.
El sistema a evaluar es el sistema integrado (SI), con respecto a un sistema convencional (subsistema I). Para ello, se identificaron las variables y parámetros del subsistema I, con un subíndice o, indicando que este es el sistema convencional.
Tabla 2 Parámetros requeridos por los objetivos del problema
Aplicación de los algoritmos evolutivos
La presencia de múltiples objetivos en un problema, además de requerir de un método de resolución no convencional, da lugar a un grupo de soluciones óptimas conocidas ampliamente como soluciones óptimas de Pareto [14].
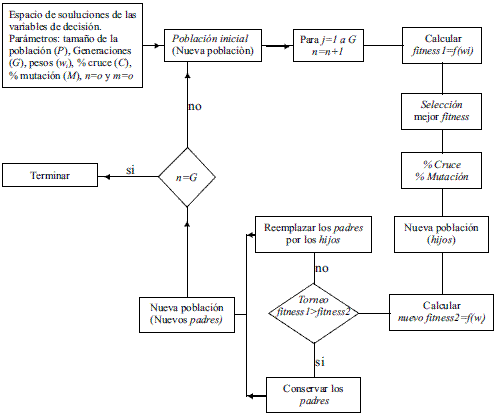
Figura 2 Diagrama de flujo del AG con fitness en función de pesos de importancia
Los métodos evolutivos como la programación evolutiva, las estrategias evolutivas y los algoritmos genéticos (AG) son los más utilizados para estos casos [1, 7, 14]. En lo particular empleamos AG, con el que se construye el grupo de soluciones óptimas a partir de la asignación de pesos de importancia para cada función objetivo. En la figura 2, se muestra el diagrama de flujo del algoritmo genético por pesos, en el que se identifican cada paso requerido para que se alcance la optimización para el caso particular de este trabajo.
Los AG’s son una representación simple de la evolución biológica, en la que un par de padres de una población de individuos demarcados en una generación (selección), dan origen a un par de hijos con características de los padres (cruzamiento). Los individuos que forman la próxima generación se escogen por torneo, en el que gana el que tenga mejor aptitud (fitness) frente a los criterios del evaluador, con lo que la optimización va evolucionando hacia mejores valores en las próximas generaciones. Antes de la evaluación del fitness, se estima un porcentaje pequeño de mutación con el que hay un probable cambio de alguna característica del individuo.
En nuestro caso, el fitness está constituido por la suma ponderada de los objetivos a los cuales se les asigna un peso según la preferencia del evaluador, tal como se representa en la ecuación 4.
Donde w1 + w2 + w3 = 1, es la suma de los pesos asignados a cada objetivo.
Resultados y discusión
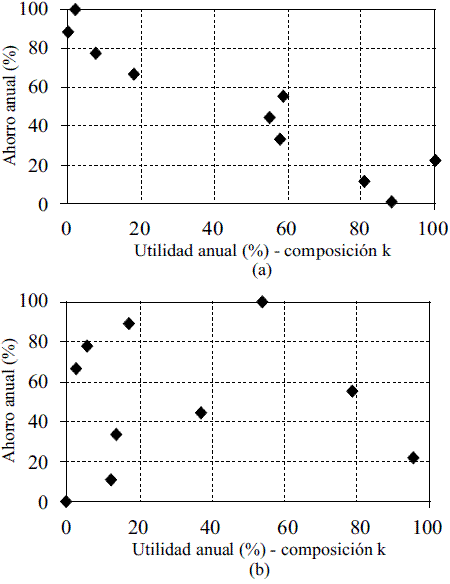
Inicialmente se verifica si los objetivos tratados, son contradictores o colaboradores. Para el caso del comportamiento del objetivo tecnológico en función del termoeconómico, se muestra que hay una dependencia por la influencia de la composición del combustible. La figura 3a, muestra que cuando la composición del combustible es constante, hay una marcado comportamiento contradictor entre las funciones objetivo consideradas.
Cuando la composición de combustible es variable, este comportamiento no es claro, presentándose algunos casos de comportamiento colaborativo, como lo muestra la figura 3b. Para todos los casos, se considera el precio de la exergía producida constante (sin incertidumbre).
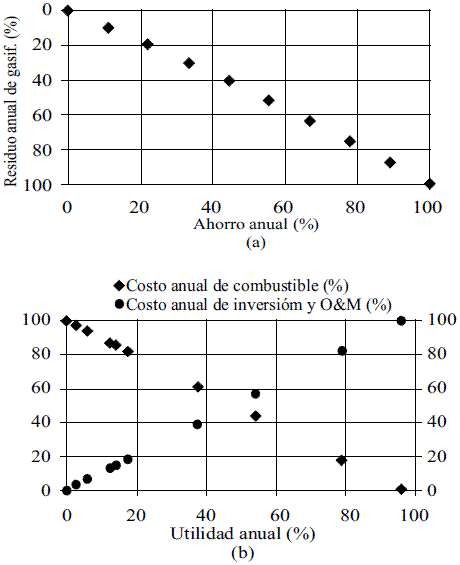
La figura 4a, muestra que el objetivo ambiental es absolutamente contradictor al tecnológico y por ende cuando la composición de combustible es variable, el objetivo termoeconómico cambia de comportamiento, según sea el cambio en la composición del combustible. La razón de estos cambios, se debe a la distribución de costos del sistema. Se muestra claramente, en la figura 4b, que el objetivo termoeconómico es afectado por la distribución de costos, es contradictor a los costos de combustibles, pero colaborador a los costos de inversión y O&M, razón por la cual, para una composición variable de combustible, se presenta el fenómeno de colaboración y contradicción de objetivos para un mismo proceso.
Figura 3 Utilidad contra ahorro a composición de combustible (a) constante y (b) variable
Figura 4 a) Ahorro contra producción de residuos. b) Utilidad contra costos de combustible - de inversión y O&M
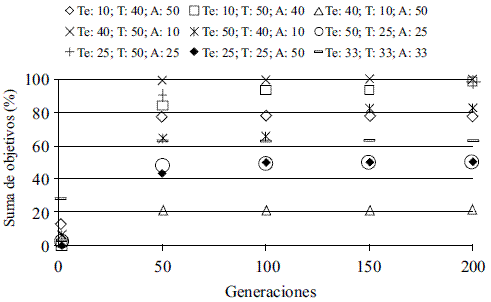
La figura 5, obtenida de la optimización aplicando los pasos del diagrama de algoritmos evolutivos (AE) de la figura 2 y aplicando la ecuación 4, muestra la influencia de pesos de importancia para elegir un óptimo cuando se tienen varios objetivos. Lo más relevante que muestra esta figura, es la influencia del objetivo ambiental en los otros objetivos y la predominancia del objetivo tecnológico. Cuando se le asigna un peso alto al objetivo ambiental, se observa que los objetivos termoeconómico y tecnológico se afectan, en algunos casos considerablemente.
Figura 5 Generaciones de optimización con pesos
Cuando el objetivo ambiental se le da un peso de 50, el objetivo global no supera el 80%; la curva más alta se obtiene cuando el objetivo tecnológico se le asigna un valor de 40. Si observamos las curvas cuando el objetivo tecnológico tiene peso 50, se obtienen los valores globales más altos, lo que indica que este objetivo predomina sobre los otros.
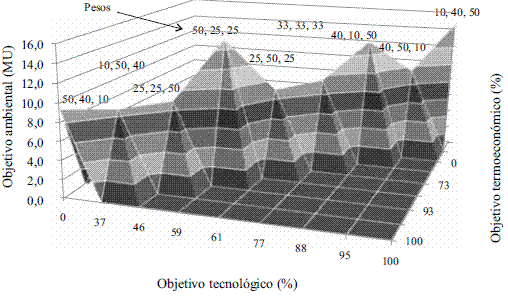
La figura 6, muestra la influencia de los pesos en la optimización del problema MO con AE, en el que se configura la frontera Pareto-óptima a partir de la obtención del fitness. Tal como se explicó anteriormente, el objetivo ambiental condiciona los otros objetivos. El mejor valor se muestra cuando los pesos son de 25 para el objetivo termoeconómico, 50 para el tecnológico y 25 para el ambiental, donde se obtiene valores medios para cada objetivo.
Figura 6 Curva de Óptimos de Pareto a partir de pesos
Conclusiones
La evaluación de las ecuaciones globales del problema multiobjetivo, sin llegar a valores de optimización presentan alta variabilidad frente a pequeños cambios en la eficiencia, tienen comportamiento no lineal y están sujetas a la inclusión de variables por el efecto del entorno, lo que sugiere considerar un método no convencional para una optimización que permita encontrar diferentes alternativas de solución y no caer en óptimos locales. La inclusión del objetivo ambiental, desde el punto de vista de generación de residuos, muestra implicaciones importantes en la optimización como la inclusión de nuevas variables de decisión, tales como la fracción, la calidad y cantidad de los combustibles disponibles.
Agradecimientos
A COLCIENCIAS, por apoyar con la beca doctoral de M.B. ay udando a materializar este trabajo.
Referencias
1. P. K. Sahoo. Exergoeconomic Analysis and Optimization of a Cogeneration System Using Evolutionary Programming. Applied thermal engineering. Vol. 28. 2007. pp. 1580-1588. [ Links ]
2. A. Lozano, A. Valero. Theory of the Exergetic Cost. Energy. Vol. 18. 1993. pp 939 - 960. [ Links ]
3. A. Bejan, G. Tsatsaronis, M. Moran. Thermal Design and Optimization. Ed. Jhon Wiley and Sons. Inc. New York. 1996. pp. 463-513. [ Links ]
4. G Tsatsaronis. Thermoeconomic Analysis and Optimization of Energy Systems. Progress in energy and combustion. Vol. 19. 1993. pp. 227-257. [ Links ]
5. G. Tsatsaronis, J. Pisa. Exergoeconomic Evaluation and Optimization of Energy Systems - Application to the CGAM Problem. Energy. Vol. 19. 1994. pp. 287-321. [ Links ]
6. R. Garduno-Ramirez, K.Y. Lee. Multiobjective Optimal Power Plant Operation Through Coordinate Control with Pressure Set Point Scheduling. IEEE Transactions on Energy Conversion. Vol. 16. 2001. pp. 115-122. [ Links ]
7. B. Galvan, D. Greiner, G. Winter. Una Comparativa de Algoritmos Evolutivos Multicriterio en Diseños de Sistemas de Seguridad. Segundo Congreso Español de Metaheurísticas, Algoritmos Evolutivos y Bioinspirados. MAEB03. Guijón (España). pp. 468-475. [ Links ]
8. A. C. Caputo, P. M. Pelagagge, P. Salini. Heat Exchanger Design Based on Economic Optimisation. Applied Thermal Engineering. Vol 28. 2008. pp. 1151-1159. [ Links ]
9. K. Deb, A. Pratap, S. Agarwal, T. Meyarivan. A Fast and Elitist Multiobjective Genetic Algorithm: NSGAII, IEEE Transactions on Evolutionary Computation. Vol. 6. 2002. pp. 182-197. [ Links ]
10. V. Manzur. Fuzzy Thermoeconomic Optimization of Energy-Transforming Systems, Applied Energy. Vol. 84. 2007. pp. 749-762. [ Links ]
11. C. Giannantoni, A. Lazzaretto, A. Macor, A. Mirandola, A. Stoppato, S. Tonon S. Ulgiati. Multicriteria Approach for the Improvement of Energy Systems Design. Energy. Vol. 30. 2005. pp. 1989-2016 [ Links ]
12. National Energy Technology Laboratory (NETL). United States Department of Energy. EUA. Gasification Alternatives for Industrial Applications. Ed. Nesant & GTI. San Francisco (CA). 2007. pp. 1-24. [ Links ]
13. L. Duan, Y. Yang, Comparative Study on Different IGCC Systems with Quasi-Zero. CO2 Emission. Int. J. of Thermodynamics. Vol. 10. 2007 pp. 61-69. [ Links ]
14. S. Alvarado, C. Gherardelli. Input-Output Exergo- Economic Optimization of Multicomponent- Multiproducts Systems Methodology. Energy. Vol. 19. 1994. pp 251-258. [ Links ]
(Recibido el 20 de febrero de 2009. Aceptado el 21 de agosto de 2009)
*Autor de correspondencia: teléfono: + 57 + 4 + 425 53 00, fax + 57 + 4 + 230 5351, correo electrónico: mjbastid@unalmed.edu.co (M. Bastidas).