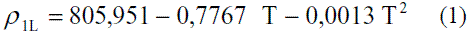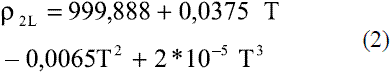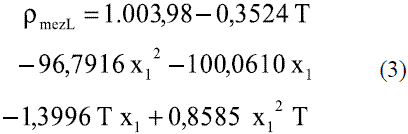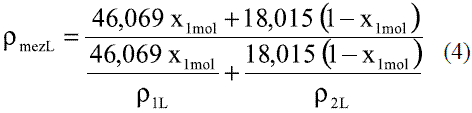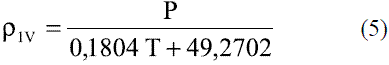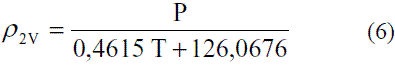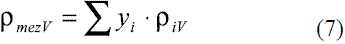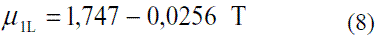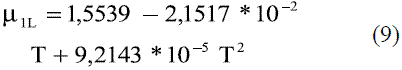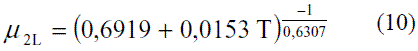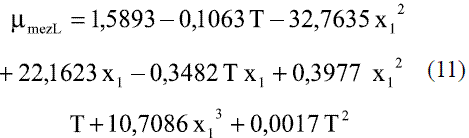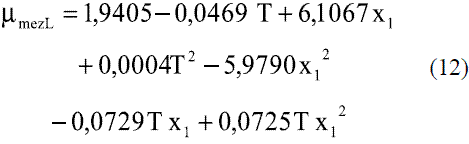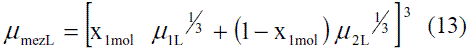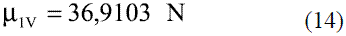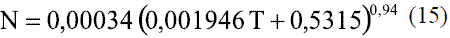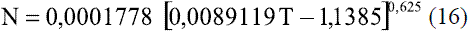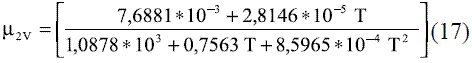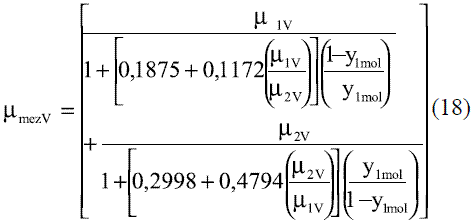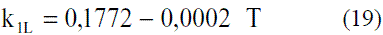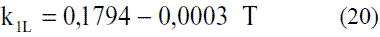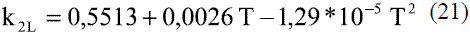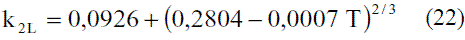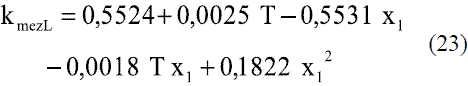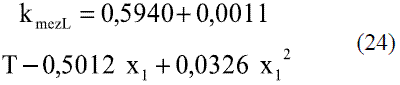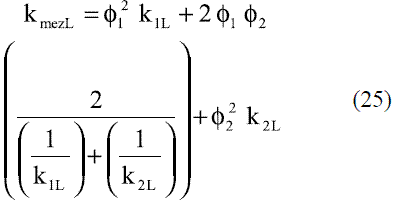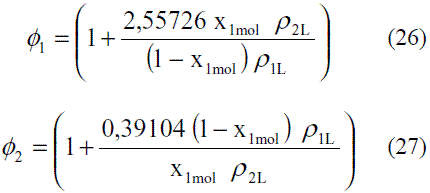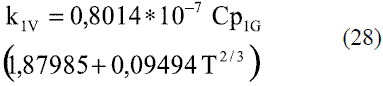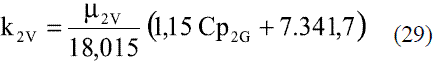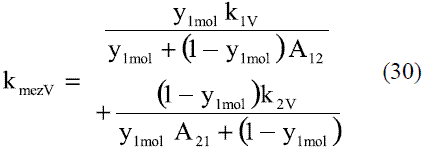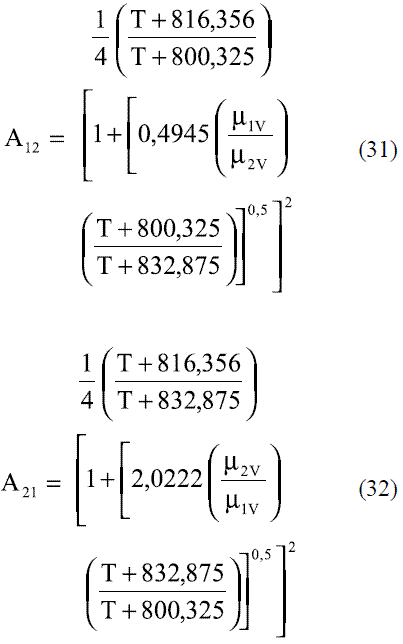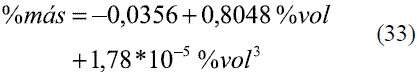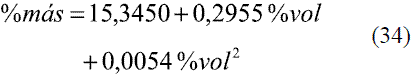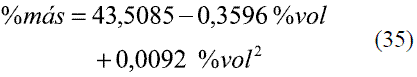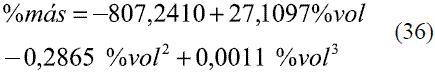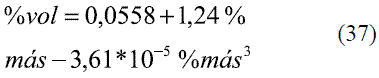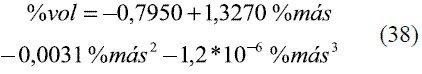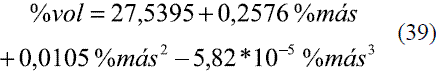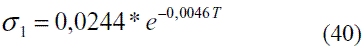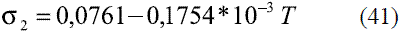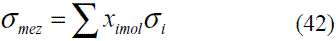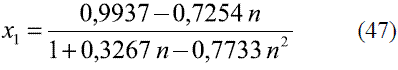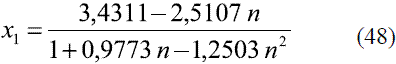Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230On-line version ISSN 2422-2844
Rev.fac.ing.univ. Antioquia no.52 Medellín Apr./June 2010
Evaluación de propiedades físicas de mezclas etanol-agua (II)
Evaluation of physical properties of ethanolwater mixtures (II)
Osney Pérez Ones*, Jorge Díaz Rodríguez, Lourdes Zumalacárregui, Osvaldo Gozá León
Grupo de Análisis de Procesos, Facultad de Ingeniería Química, Instituto Superior Politécnico José Antonio Echeverría Ave 114 No 11901 e/ 119 y 127. Marianao, Ciudad Habana. Cuba
Resumen
En este trabajo se presentan modelos para el cálculo de las propiedades físicas en mezclas de etanol-agua a presión atmosférica. Esto se logra a través de un método rápido y sencillo con un mínimo de información, partiendo de propiedades que se puedan medir experimentalmente. Los modelos para el cálculo de algunas propiedades como: densidad, viscosidad dinámica, conductividad térmica, tensión superficial e índice de refracción, así como modelos para la conversión entre composiciones, se obtienen a partir de ajustes estadísticos. Los valores de las propiedades obtenidas con estas ecuaciones son comparados con los reportados en la literatura, mostrándose la calidad del método.
Palabras clave: Alcohol etílico, etanol, densidad, viscosidad, conductividad
Abstract
In this work, models to estimate physicals properties for ethanol-water mixtures are shown for atmospheric pressure. This is achieved through a quick and simple method with a minimum of information, starting with measurable properties. Models to estimate density, dynamic viscosity, thermal conductivity, surface tension and refractive index are based on statistic methods. Obtained values are compared with different literature sources showing, satisfactory adjustments.
Keywords: Ethyl alcohol, ethanol, density, viscosity, conductivity
Introducción
Todos los procesos químicos requieren de la disponibilidad de propiedades físicas y termodinámicas. En dependencia de la operación unitaria involucrada, las propiedades físicas y termodinámicas que se requieren son diferentes [1]. Aunque las leyes de la Termodinámica son generales, ellas suministran relaciones, no modelos. Por lo que, cuando se habla de calcular propiedades físicas se está haciendo referencia a resultados obtenidos usando modelos termodinámicos. La calidad final de los resultados en la modelación de un proceso, independientemente del grado de sofisticación de las ecuaciones del modelo, depende de la calidad de las predicciones suministradas por el modelo termodinámico [2]. En la industria competitiva actual, los procesos son modelados y optimizados usando herramientas de simulación. Una de las razones fundamentales por la cual los simuladores de procesos son exitosos, es su habilidad para modelar con precisión el comportamiento termodinámico de las mezclas de fluidos con muy poca información de entrada por parte del usuario [3]. La mayoría de los simuladores tienen una gran base de datos de componentes y una amplia variedad de modelos termodinámicos y correlaciones estadísticas incluidos en el paquete de propiedades físicas disponibles. Es por ello que el paso más propenso a errores en una simulación es la selección del modelo correcto y los datos de propiedades físicas [1]. Dado que la información relacionada con la estimación de propiedades de mezclas etanol-agua se encuentra dispersa en la literatura y que en todos los casos no se brinda la calidad del ajuste ni el error de estimación de las propiedades calculadas, en este trabajo se presentan los modelos obtenidos estadísticamente utilizando STATGRAPHICS Centurión XV. Dado que en la literatura se reportan resultados de composición unas veces en % másicos y en otras como % volumétricos, se incluyen modelos que permiten la conversión de una en otra forma de expresar la composición. Estos modelos forman parte del paquete de propiedades del simulador de procesos para fábricas de azúcar y etanol (STA).
Modelos
Densidad
Para la densidad del etanol en fase líquida en el intervalo de temperatura entre 273 y 373 K (0 y 100 oC) [4] se obtuvo el modelo siguiente:
Para determinar la densidad del agua en fase líquida en el mismo intervalo de temperatura [5] se ajustó el siguiente modelo:
Para determinar la densidad de la mezcla etanolagua en fase líquida en función de la composición y la temperatura se pueden utilizar las siguientes expresiones:
Para valores entre 0 y 80 oC
Se ajustó el siguiente modelo [6]:
Para valores entre 80 y 100 oC
Se emplea la ley de Amagat [4]
En fase vapor la densidad de los componentes puros se determina a partir de la ley de los gases ideales [4]. Para el etanol queda:
Para el agua:
Para el cálculo de la densidad de la mezcla en fase vapor puede usarse la regla aditiva:
Viscosidad Dinámica
Para determinar la dependencia de la viscosidad del etanol en fase líquida [4] en función de la temperatura se pueden utilizar las siguientes expresiones:
Para valores entre 0 y 30 oC
Para valores entre 30 y 100 oC
En el caso del agua, para determinar su viscosidad en fase líquida [5] en función de la temperatura se emplea el siguiente modelo para valores entre 273 y 373 K (0 y 100 oC):
Los estudios teóricos de la viscosidad de mezclas generalmente son complicados. Existen varios modelos empíricos propuestos con este fin. En raros casos, la viscosidad de las mezclas puede ser obtenida por la suma de las viscosidades de los componentes puros [7].
Para la estimación de la viscosidad dinámica de la mezcla etanol-agua en función de la composición y la temperatura en fase líquida, se ajustaron los siguientes modelos, válidos entre 273 y 343 K (0 y 70 oC) [6]:
Para valores de temperatura de 0-25 oC
Para valores de temperatura de 25-70 oC
Para valores de temperatura de 70-100 oC
Se utiliza la regla de mezclado desarrollada por Kendall y Monroe [4]:
Para calcular la viscosidad de los componentes puros en fase vapor, se utiliza en el caso del etanol, el método de Stiel y Thodos [4]:
Donde el parámetro N se calcula en dependencia del valor que toma la temperatura reducida:
Para valores de temperatura reducida ≤ 1,5
Para valores de temperatura reducida > 1,5
Para el agua se emplea el método de Reichenberg [4]:
En el caso de la viscosidad de la mezcla en la fase vapor se utiliza el método de Bromley y Wilkeis [4], válido a bajas presiones y temperatura reducida por debajo de 0,6:
Conductividad térmica
Las ecuaciones que se muestran a continuación permiten determinar la conductividad térmica del etanol en fase líquida en función de la temperatura para diferentes intervalos [4]:
Para valores entre 0 y 40 oC
Para valores entre 40 y 100 oC
Para determinar la conductividad térmica del agua en función de la temperatura se pueden utilizar las siguientes expresiones:
Para valores entre 0 y 90 oC
Se ajustó la ecuación [5]:
Para valores entre 90 y 100 oC
Se emplea el método de Missenard [4], válido a presiones inferiores a 3,5 MPa:
Para obtener la ecuación de la conductividad térmica de la mezcla etanol-agua en función de la composición y la temperatura en fase líquida, se ajustaron debido a las características de la curva, dos modelos. Se utilizaron los datos reportados en la literatura [6], para valores entre 273 y 353 K (0 y 80 oC):
Para valores de temperatura entre 0-40 oC
Para valores de temperatura entre 40-80 oC
Para valores de temperatura entre 80-100 oC
Se sugiere el método de Li [4], válido a presiones menores que 3,5 MPa:
Donde el parámetro Φij se determina a partir de las siguientes expresiones:
Se sugiere el método de Li [4], válido a presiones menores que 3,5 MPa:
Para la determinación de la conductividad térmica del etanol en fase vapor se utiliza la ecuación de Misic y Thodos [4], válida a presiones inferiores a 3,5 MPa:
Se sugiere el método de Li [4], válido a presiones menores que 3,5 MPa:
Para el agua se emplea la expresión de Stiel y Thodos [4] para moléculas no lineales:
Se sugiere el método de Li [4], válido a presiones menores que 3,5 MPa:
En el caso de la conductividad térmica de la mezcla en fase vapor, se utiliza la relación de Wassiljewa [4], válida para presiones igual a la atmosférica o menores que ella:
Se sugiere el método de Li [4], válido a presiones menores que 3,5 MPa:
Los parámetros de interacción binarios se determinan por el método de Lindsay y Bromley
:Conversión entre composiciones
Para determinar las ecuaciones de conversión entre % másico (oINPM) y %volumétrico (oGL) y viceversa, se ajustaron los siguientes modelos de acuerdo a los datos brindados por la literatura [6].
Para %volumétrico entre 0-73,34
Para %volumétrico entre 73,34-86,31
Para %volumétrico entre 86,31-92,53
Para %volumétrico entre 92,53-100
Para %másico entre 0-39
Para %másico entre 39-78
Para %másico entre 78-100
Tensión superficial
Para evaluar la tensión superficial del etanol en función de la temperatura se puede utilizar el siguiente modelo, válido entre 273 y 333 K (0 y 60 oC), ajustado de acuerdo a los datos brindados por la literatura [5]:
Para determinar la tensión superficial del agua en función de la temperatura [5] se ajustó la ecuación, válida entre 273 y 403 K (0 y 130 oC), que se muestra a continuación:
En el caso de las mezclas puede usarse la regla aditiva para el cálculo de la tensión superficial:
Índice de refracción
Para la determinación de la composición de etanol en la mezcla, a través de la medición del índice refracción a 293 K (20 oC), se ajustaron varios modelos para los datos reportados en la literatura [8]:
Para n entre 1,3330 - 1,3377
Para n entre 1,3377 - 1,3511
Para n entre 1,3511 - 1,3583
Para n entre 1,3583 - 1,3634
Para n entre 1,3634 - 1,3658
Para n entre 1,3646 - 1,3658 y x1 > 0,8
Resultados y discusión
En la tabla 1 se presentan algunos de los parámetros estadísticos de los modelos descritos anteriormente. En todos los casos el valor de probabilidad fue igual a cero para Fc < Fcalculadas. Los coeficientes que se reportan en cada modelo resultaron significativos para más de 95% de confianza utilizando para ello el criterio de la t de Student.
La confiabilidad de los modelos ajustados puede observarse en la Tabla 2.
Para los modelos representados por las ecuaciones 4-7, 13-18, 25-32 y 42 no se reportan valores ya que estas ecuaciones no fueron obtenidas por los autores.
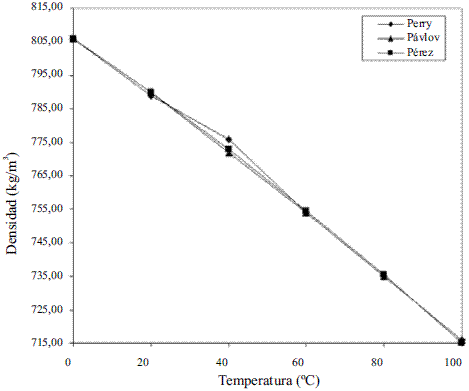
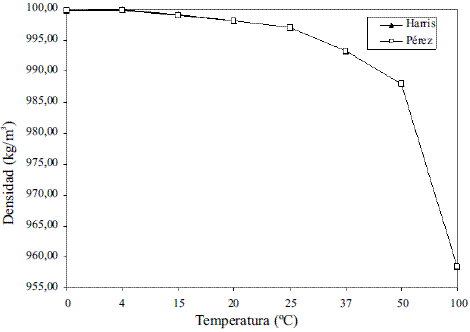
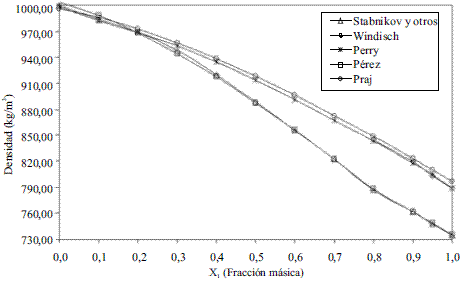
El modelo ajustado (Ec. 1) representado en la figura 1 se muestra la densidad de etanol en fase líquida que fue comparada con los datos de la literatura, Perry [4] y Pávlov [5], dando un error promedio de 0,13% y 0,06%, respectivamente. El modelo ajustado (Ec. 2) para la densidad de agua en fase líquida (Figura 2) fue comparado con los datos de la literatura, Pávlov [5] y Engineeringtoolbox [9], dando un error promedio de 0,02% y 0,01%. También se comparó con los valores reportados por Harris [10] (Figura 3), obteniéndose como error promedio 0%. Los resultados obtenidos para la densidad de la mezcla en fase líquida, entre 273 y 353 K, (Ec. 3) fueron comparados con Stabnikov y otros [6], Windisch [11], Perry [4] y Konchady [12], dando errores promedios de 0,18%, 4,03%, 3,59% y 4,72%, respectivamente. Se puede apreciar en la figura 4, que el modelo propuesto a bajas concentraciones de etanol predice un buen comportamiento, todo lo contrario cuando aumentan las concentraciones, ya que se nota un alejamiento en comparación con otros autores. Con la aplicación de la ecuación de Amagat (Ec. 4) se obtiene como error promedio 1,81%. Los resultados que se obtienen para la densidad del agua en fase vapor (Ec. 6), se compararon a presión atmosférica en el intervalo entre 100-400 0C, con los obtenidos a partir de las funciones para el cálculo de propiedades termodinámicas y de transporte del agua y el vapor de la norma industrial IAPWS-IF97, obteniéndose como error promedio 0,49%.
Tabla 1 Parámetros estadísticos de los modelos
Tabla 2 Confiabilidad de los modelos
Figura 1 Densidad del etanol en fase líquida
Figura 2 Densidad del agua en fase líquida
Figura 3 Densidad del agua en fase líquida (Harris [10])
Figura 4 Densidad de la mezcla etanol-agua
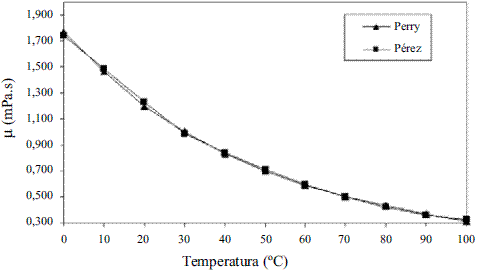
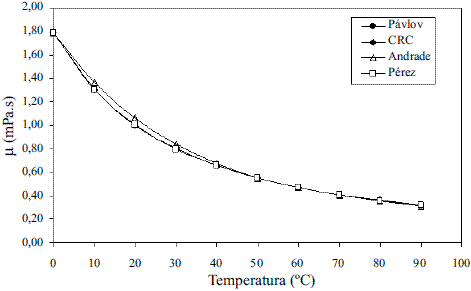
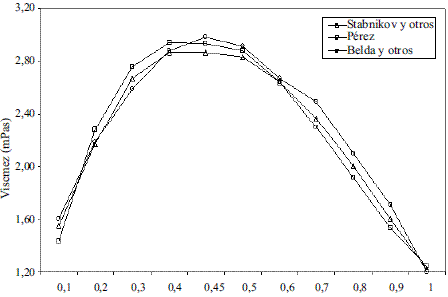
Los modelos obtenidos para evaluar la viscosidad dinámica del etanol en fase líquida (Ec. 8 y 9) fueron comparados con los de Perry [4], dando un error promedio de 1,50%; esto se puede observar en la figura 5. La comparación del modelo obtenido para el agua (Ec. 10) reflejado en la figura 6, con los resultados que brindan Pávlov [5], Lide [13] y Andrade [14], arrojan un error promedio de 0,30%, 0,33% y 1,92%. En las figuras 5 y 6, se aprecia cómo la viscosidad de ambas sustancias en fase líquida disminuye exponencialmente con la temperatura. Esto concuerda con el comportamiento observado en la mayor parte de los líquidos puros [14]. Los modelos obtenidos (Ec. 11 y 12), se compararon con los resultados de Stabnikov y otros [6] y los de Belda y colaboradores [15], dando como error promedio 4,14% y 4,52%, respectivamente; para la Ec. 13 se reporta [4] que presenta un error entre 5-6%. Se puede observar en la figura 7 que el mayor alejamiento está en el intervalo de composición de 0,2 a 0,7 en ambos casos. Para los modelos que permiten calcular la viscosidad de los componentes puros en fase vapor, se reporta [4] que, en el caso de la Ec. 14, el error es inferior al 3% y la Ec. 17 presenta un error cercano al 5%. En el caso de la viscosidad de la mezcla en la fase vapor (Ec. 18), presenta un 3% de error [4].
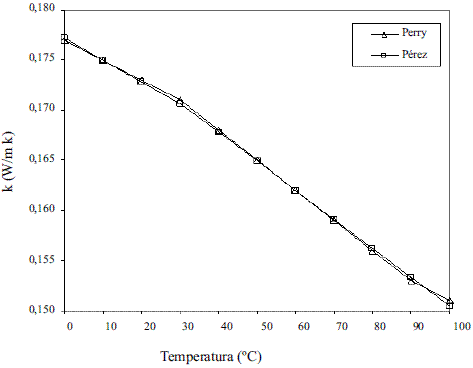
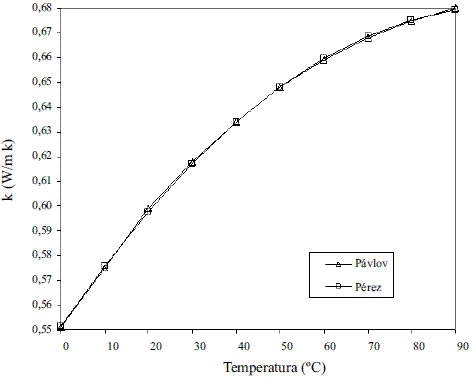
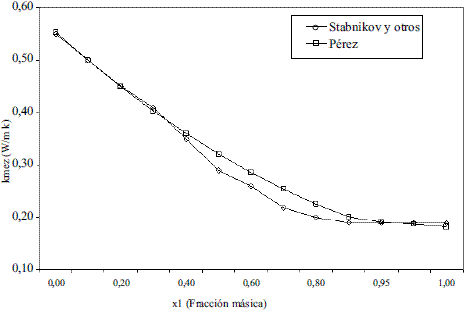
Los modelos obtenidos (Ec. 19 y 20), que permiten evaluar la conductividad térmica del etanol en fase líquida (Figura 8), fueron comparados con los de Perry [4], dando un error promedio de 0,13%. En el caso del agua, el modelo obtenido (Ec. 21) fue comparado con los resultados del Pávlov [5], presentando un error promedio de 0,10%. Estos resultados pueden apreciarse en la figura 9. Para la Ec. 22 se informa [4] un error inferior al 8%. Los modelos obtenidos para la mezcla etanol-agua en fase líquida (Ec. 23 y 24), se compararon con los datos de Stabnikov y otros [6], dando como error promedio 4,76%; se observa en la figura 10 que hay un pequeño alejamiento en el intervalo de composición de 0,4 a 0,95. El comportamiento de la conductividad térmica de la mezcla es similar al obtenido por Jowitt y colaboradores [16]. Para la Ec. 25 se informa [4] que presenta un error entre 4-6%. En el caso de los modelos que permiten, calcular la conductividad térmica de los componentes puros en fase vapor (Ec. 28 y 29), se reportan [4] errores inferiores al 5% y entre 8-10%, respectivamente. Para la conductividad térmica de la mezcla en fase vapor (Ec. 30), el error está entre 4-5%.
Figura 5 Viscosidad dinámica del etanol
Figura 6 Viscosidad dinámica del agua
Figura 7 Viscosidad dinámica de la mezcla etanolagua
Figura 8 Conductividad térmica del etanol
Figura 9 Conductividad térmica del agua
Figura 10 Conductividad térmica de la mezcla etanol-agua a 0 (oC)
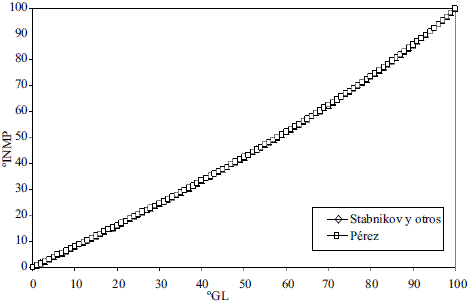
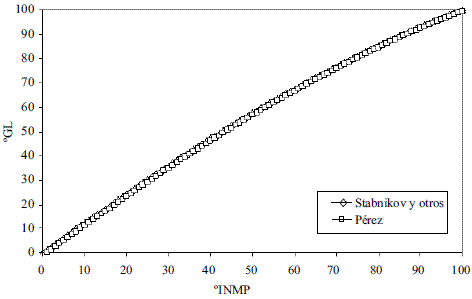
Para la conversión de oINPM a oGL (Ec. 33-36), y de oGL a oINPM (Ec. 37-39) se obtuvieron varias ecuaciones para diferentes intervalos. Los resultados fueron comparados con Stabnikov y otros [6], dando un error promedio de 0,09% y 0,08%, respectivamente. Los datos comparados se evaluaron en todo el intervalo de composiciones y se muestran en las figuras 11 y 12.
Figura 11 Conversión de oGL a oINPM
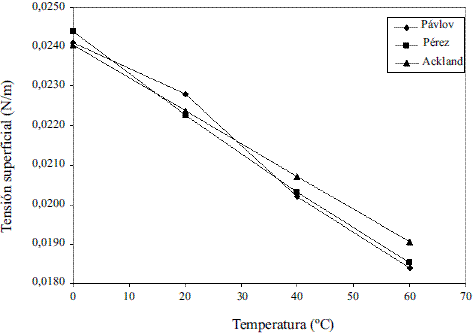
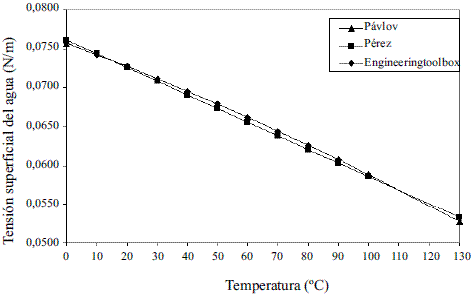
El modelo ajustado (Ec. 40) representado en la figura 13 muestra la tensión superficial de etanol que fue comparada con los valores que ofrece el modelo de Ackland [17], presentando un error promedio de 1,68%. En el caso del agua el modelo obtenido (Ec. 41) fue comparado con los resultados reportado en Engineeringtoolbox [18], dando un error promedio de 0,60%. Estos resultados pueden apreciarse en la figura 14. El modelo para la mezcla (Ec. 42) fue validado con anterioridad por Belda y colaboradores [19].
Figura 12 Conversión de oINPM a oGL
Figura 13 Tensión superficial del etanol Pávlov
Figura 14 Tensión superficial del agua
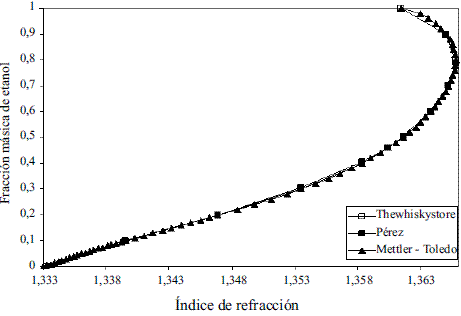
La comparación de los modelos obtenidos (Ec. 43-48) reflejados en la figura 15 con los resultados que brinda Thewhiskystore [20], dan un error promedio de 0,71%. Por otra parte se han reportado estudios en la literatura que afirman que la ecuación de Gladstone-Dale [21] ofrece resultados satisfactorios en la predicción del índice de refracción en función de la composición y densidad de la mezcla.
Figura 15 Índice de refracción de la mezcla etanolagua respecto al aire a 20 oC
Conclusiones
Se obtuvieron los modelos que permiten calcular propiedades físicas y termodinámicas de las mezclas etanol-agua como: densidad, viscosidad dinámica, conductividad térmica, tensión superficial e índice de refracción.
Al ser comparados con la bibliografía existente, se puede considerar que los modelos desarrollados en este trabajo, en general, son confiables y pueden ser utilizados para la estimación de las propiedades de la mezcla etanol-agua. Las desviaciones de estos valores con respecto a los reportados por la literatura, se encuentran dentro del intervalo permisible de error para este tipo de trabajo. Los errores en las estimaciones son menores al 5%, en su mayoría.
Nomenclatura



Referencias
1. L. Venkatesh. Choice of thermodynamic models for use in simulation programs. Chemical Engineering World. Vol. 32. 1997. pp. 155-157. [ Links ]
2. Why rigorous thermodynamics?. http://www.virtualmaterials.com. Consultada el 20 de octubre de 2001. [ Links ]
3. M. A. Satyro. Thermodynamics and the simulation engineer. Chemical Product and Process Modeling. Vol. 3, 2008. Article 24. The Berkeley Electronic Press. Available at: http://www.bepress.com/cppm/vol3/iss1/24. [ Links ]
4. R. H. Perry, D. W. Green. Manual del Ingeniero Químico. 6a. ed. McGraw-Hill. México. 1999. Sección 2. pp. 112-370. [ Links ]
5. K. F. Pávlov. Problemas y ejemplos para el curso de operaciones básicas y aparatos en tecnología química. Editorial MIR, Moscú. 1981. pp. 547-560. [ Links ]
6. B. N. Stabnikov, I. M. Roiter, T. B. Prostok. Alcohol etílico. Manual. Editora Industria Alimentaria. Moscú. 1976. pp. 10-98. [ Links ]
7. J. V. Herráez, R. Belda, O. Diez. An equation for the correlation of viscosities of binary mixtures. Journal of Solution Chemistry. Vol. 37. 2008. pp. 233-248. [ Links ]
8. Ethanol refractometry concentration. Mettler-Toledo International Inc. http://us.mt.com/mt/ed/appEdStyle/Ethanol_re_e_0x000248e10002599200076b0e.jsp. Consultada el 20 de enero de 2009. [ Links ]
9. Densities of water in SI Units. http://www.engineeringtoolbox.com/water-density-specificweight-d_595.html. Consultada el 15 de noviembre de 2008. [ Links ]
10. D. Harris. Quantitative Chemical Analysis, 4a. ed. Ed. W. H. Freeman and Company, New York. 1995. pp. 36. [ Links ]
11. Departamento Control de Laboratorios. Dirección de Producción y Entrega. Viceministerio para la Producción. Tablas para el trabajo analítico en los laboratorios de las destilerías y plantas anexas de levadura seca. MINAZ S/A. pp. 1-16. [ Links ]
12. S. Konchady. Alcohol palm book. . Praj Industries Limited. India. 2a. ed. 2004. pp. 12-45. [ Links ]
13. D. R. Lide. CRC Handbook of Chemistry and Physics. 84a. ed. online version. CRC Press. Boca Raton (Florida). 2003. pp. 2256-2257. [ Links ]
14. R. C. Reid, J. M. Prausnitz, B. E. Poling. The properties of gases and liquids. McGraw Hill Book Company. New York. 4a. ed. 1987. pp. 433-473. [ Links ]
15. R. Belda, José V. Herráez, O. Diez. Rheological study and thermodynamic analysis of the binary system (water/ethanol): Influence of concentration. Physics and Chemistry of Liquids. Vol. 42. 2004. pp. 467-479. [ Links ]
16. R. Jowitt, F. Escher, B. Hallström, H. F.T. Meffert, W. E. L Spiess, G. Vos. Physical properties of foods. Applied Science Publishers. London. 1983. pp. 295- 296. [ Links ]
17. T. Ackland. Ethanol-water physical properties. http://homedistiller.org/calc.htm. Consultada el 28 de enero de 2009. [ Links ]
18. Surface tension of water in contact with air for temperatures ranging 0-100oC. http://www.engineeringtoolbox.com/water-surfacetension-d_597.html. Consultada el 25 de enero de 2009. [ Links ]
19. R. Belda, J. V. Herráez, O. Díez. A study of the refractive index and surface tension synergy of the binary water/ethanol: influence of concentration. Physics and Chemistry of Liquids. Vol. 43. 2005. pp. 91-101. [ Links ]
20. Alcohol and water. Some physically data: Ethanol water refractive index to air (20 oC). http://www.thewhiskystore.de/experts/alcohol.htm. Consultada el 26 de enero de 2009. [ Links ]
21. J. V. Herráez, R. Belda. Refractive indices, densities and excess molar volumes of monoalcohols + water. Journal of Solution Chemistry. Vol. 35. 2006. pp. 1315-1328. [ Links ]
(Recibido el 23 de septiembre de 2009. Aceptado el 8 de enero de 2010)
*Autor de correspondencia: teléfono: + 53 + 7 + 266 33 96, correo electrónico: osney@quimica.cujae.edu.cu.(O. Perez)